弱Ding-投射模及相关维数

何东林，张金战

（陇南师范高等专科学校数信学院，甘肃 陇南 742500）

引 言

Gorenstein同调理论是相对同调代数的重要研究课题之一.Auslander和Bridger[1]介绍了双边Noether环上有限生成模的G-维数.Enochs和Jenda[2]给出了一般环上Gorenstein内射模和Gorenstein投射模的定义.随后，许多学者先后对其进行了研究和推广.特别地，Holm和Jørgensen[3]在交换Noether环上引入了C-Gorenstein内射模和C-Gorenstein投射模，并研究了与它们相关的投射维数.White[4]进一步讨论了一般Noether环上C-Gorenstein内射模和C-Gorenstein投射模，并称之为GC-内射模和GC-投射模.Gillespie[5]介绍了Ding-投射模和Ding-内射模的概念.Ding-投射模与强Gorenstein平坦模[6]是一致的，而Ding-内射模与Gorenstein FP-内射模[7]是一致的.为了研究Ding-投射模和Ding-内射模的可数部分及相关模类，Zhang等[8]介绍了关于半对偶模的Ding-投射模，其概念与C-平坦模紧密相连.C-f-投射模[9]是介于C-投射模与C-平坦模之间的一类模.何东林等[10]引入关于半对偶模的弱Ding-投射模，它与C-f-投射模紧密相连，是关于半对偶模的Ding-投射模的一个重要推广.本文将进一步讨论关于半对偶模的弱Ding-投射模的若干性质，及与其相关的弱Ding-投射维数，研究模M的弱Ding-投射维数小于等于n的若干等价刻画.

文中的环R均指有单位元的交换环，模均指酉R-模.如果R-模C满足条件（1）C具有有限生成投射分解，（2）R≅Hom（C，C）且则称 C 是半对偶模.如果对R-模M的任意有限生成子模K，都存在有限生成自由模Rn及R-模同态α:Rn→M和β:K→Rn，使得i＝αβ，其中i:K→M是标准的包含同态，则称M是f-投射模[11].记是投射模是平坦模是f-投射模}，分别称其中的模为C-投射模、C-平坦模[12]和C-f-投射模[9].易知C-f-投射模类关于扩张、满同态的核、直和及直和因子封闭，且有称模M是C-Gorenstein投射模[3]，如果存在HomR（-，PC（R））-正合的正合列…→P1→P0→其中Pi（i∈Z）是投射模，使得M≅Coker（P1→P0）.用GPC（R）表示所有C-Gorenstein投射R-模组成的类.称模U是DC-投射模[8]（即关于半对偶模C的Ding-投射模），如果存在HomR（-，FC（R））-正合的正合列其中P（ii∈Z）是投射模，使得U≅Coke（rP1→P0）.用DPC（R）表示所有DC-投射模组成的类.设x是一个R-模类，称x是投射可解的[13]，如果x包含所有投射模且关于扩张和满同态的核封闭.分别记对任意 X∈x有对任意X∈x有下文中的C均指固定的半对偶双模RCR，其余未涉及的概念和记号参见[14-15].

1 定义和引理

先介绍一些概念和已知结论.

定义1[10]称模U是弱DC-投射模，如果存在正合的正合列

其中Pi（i∈Z）是投射模，使得U≅Coker（P1→P0）.用wDPC（R）表示所有弱DC-投射模组成的类，且称正合列（*）为弱Ding PPC-分解.

引理1[8]设P是投射模，则P∈DP（CR）且

例1因为每个R-模都具有投射分解，由引理1易知，每个R-模都具有DC-投射分解，即存在正合列…→D1→D0→M→0，其中Di（i≥0）是DC-投射模.又因为DC-投射模一定是弱DC-投射模，所以每个R-模都具有弱DC-投射分解.

引理2[10]弱DC-投射模类wDPC（R）是投射可解的，且关于任意直和因子均封闭.

引理3[10]设M是R-模，则以下条件等价：

（1）M是弱DC-投射模；

定义2设M是R-模，称M的弱DC-投射维数小于等于n，如果存在正合列

其中Wi（0≤i≤n）是弱DC-投射模，并记为wDPC-pd（M）≤n.称wDPC-pd（M）＝inf{n wDPC-pd（M）≤n}为模M的弱DC-投射维数.

2 主要结果

下面给出关于半对偶模C的弱Ding-投射模的若干性质.

命题1弱Ding PPC-分解的每个核都是弱DC-投射模.

下证Ki（i≤－2）是弱DC-投射模.根据引理3可知，只需证对任意由且知，用函子作用于正合列后可得如下长正合列又因为正合的，所以由的任意性可知，再考虑短正合列依次类推可得Ki（i≤－2）是弱DC-投射模.

综上所述，弱Ding PPC-分解的每个核都是弱DC-投射模.

命题2设M是R-模，则以下条件等价：

（1）M是弱DC-投射模；

证明 （1）⇒（2）由命题1易证.

（2）⇒（1）由M1是弱DC-投射模及引理3可得，且存在正合的正合列

命题3设0→L→M→N→0是R-模正合列，如果L和M都是弱DC-投射模，那么以下条件等价：

（1）M是弱DC-投射模；

证明 由文献[8]中推论1.5的证明过程易证.

定理1设0→H→W1→W0→M→0是R-模正合列，其中W0和W1是弱DC-投射模，则存在正合列0→H→W→Q→M→0和其中Q和Q′是投射模，且W和W′是弱DC-投射模.

证明 由W0是弱DC-投射模及定义1知，存在正合列其中Q是投射模且是弱DC-投射模.令K＝Ke（rW0→M）.考虑正合交换图，如图1和图2.

图1 K→W0与Q→W0的拉回图

图2 W1→K与U→K的拉回图

由W1是弱DC-投射模及定义1知，存在正合列其中Q′是投射模且是弱DC-投射模.考虑推出图，如图3和图4.

图3 的推出图

图4 K→W0与K→V的推出图

定理 2 设 0→H→Wn－1→Wn－2→…→W1→W0→M→0是 R-模正合列，其中Wi（0≤i≤n－1）是弱DC-投射模，则以下结论成立：

（2）存在正合列 0→V→Pn－1→Pn－2→…→P1→P0→M→0和 0→X→V→H→0，其中Pi（0≤i≤n－1）是投射模且X是弱DC-投射模.

证明（1）对n用数学归纳法.当n＝1时，0→H→W0→M→0正合，其中W0是弱DC-投射模.由命题2和引理3可知，存在正合的正合列0→W0→其中Q0是投射模且W是弱DC-投射模.考虑推出图，如图5.

图5 的推出图

图5中间行和第三列就是满足要求的正合列.

假设结论对于n－1（n≥2）成立，下面讨论对于n的情形.在正合列0→H→Wn－1→Wn－2→…→W1→W0→M→0中，Wi（0≤i≤n－1）是弱DC-投射模，不妨令I＝Im（Wn－2→Wn－3），则该正合列可分为如下两个正合列

和

根据定理1及正合列（5）可得，存在正合列

其中Qn－1是投射模且是弱DC-投射模.取将正合列0→K→与序列（6）拼接可得正合列

由归纳假设可知，存在正合列

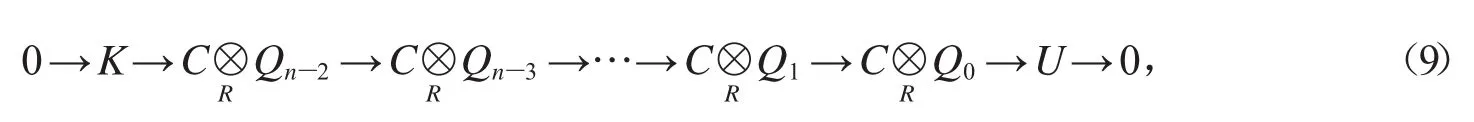
和

其中Qi（0≤i≤n－2）是投射模且W是弱DC-投射模.将序列与（9）拼接可得正合列

易知正合列（10）和（11）就是满足要求的正合列.从而结论对于n也成立.

综上所述，结论成立.

（2）证明过程与（1）对偶.

命题4设M是R-模，如果存在正合列

和

证明 由引理2和文献[1]中引理3.12易证.

基于以上结论，下面给出模M的弱Ding-投射维数wDPC-pd（M）小于等于n的若干等价刻画.

定理3设M是R-模，n为非负整数且wDPC-pd（M）＜＋∞，则以下条件等价：

（1）wDPC-pd（M）≤n；

（2）存在 R-模正合列 0 → Kn→ Wn－1→ Wn－2→…→ W1→ W0→ M → 0，其中 Wi（0≤i≤n－1）是弱DC-投射模且Kn也是弱DC-投射模；

证明（1）⇔（2）显然成立.

（2）⇒（3）设N是任意C-f-投射模R-模，根据引理3得，对任意0≤i≤n－1有等式成立.用函子HomR（-，N）作用于正合列0→Kn→Wn－1→Wn－2→…→W1→W0→M→0，由维数转移公式可得，对任意j≥n＋1有

其中Qi（0≤i≤m）是C-f-投射模.由（2）知，对任意0≤i≤m有用函子HomR（M，-）作用于序列0→Qm→Qm－1→Im－1→0，其中Im－1＝Im（Qm－1→Qm－2），得长正合列

（4）⇒（1）因为 wDPC-pd（M）＜＋∞，不妨令 wDPC-pd（M）＝k＜＋∞.若 k≤n，则结论显然成立.若k≥n＋1，则存在正合列

其中Wi（0≤i≤k）是弱DC-投射模.取Ii＝Im（Wi→Wi－1），由（4）和维数转移公式知，对任意 C-f-投射模 N 和整数 j≥n＋1，有从而有等式成立.又由维数转移公式可知，对任意整数 n≤i≤k，有根据命题3可得，Ii（n≤i≤k）是弱DC-投射模.因此结论wDPC-pd（M）≤n成立.

定理4设0→X′→X→X″→0是R-模正合列，n为非负整数，则以下结论成立：

（1）若 wDPC-pd（X′）≤n 且 wDPC-pd（X″）≤n，则 wDPC-pd（X）≤n.

（2）若 wDPC-pd（X″）≤n 且 wDPC-pd（X）≤n，则 wDPC-pd（X′）≤n.

（3）若 wDPC-pd（X′）≤n 且 wDPC-pd（X）≤n，则 wDPC-pd（X″）≤n＋1.

证明对任意C-f-投射模N，用函子HomR（-，N）作用于序列0→X′→X→X″→0可得长正合列.

（1）若 wDPC-pd（X′）≤n 且 wDPC-pd（X″）≤n，则由引理 2 知，

（2）若 wDPC-pd（X″）≤n 且 wDPC-pd（X）≤n，则由引理 2 知，

（3）若 wDPC-pd（X′）≤n 且 wDPC-pd（X）≤n，则由引理 2 知，