X-丁投射模

吴德军, 宋梦钰

(兰州理工大学 理学院, 甘肃 兰州 730050)

在本文中,R表示有单位元的结合环,所有的模都是右R-模,X表示包含所有平坦R-模的类,P(R)表示投射模类,X-Dpd(R)<∞表示环R上的整体X-丁投射维数有限,R-Mod表示R-模范畴.2009年,Ding等[1]引入了一般环上的强Gorenstein平坦模的概念.2010年,Gillespie[2]将强Gorenstein平坦模重新命名为丁投射模并且证明了丁模类和Gorenstein模类具有类似的性质.2010年,Bennis和Ouarghi[3]引入了X-Gorenstein投射模,证明了对X-Gorenstein投射模而言,Gorenstein投射模的一些结论仍然成立. 2013年,Yang等[4]研究了一般环上丁投射模的相关性质.本文在文献[3-4]的基础上引入了X-丁投射模,即如果存在正合列P=∶…→P1→P0→P0→P1→…,其中Pi,Pi是投射模,i∈Z,对于任意R-模F∈X,HomR(-,F)作用在正合列P上保持正合,并且M=Ker(P0→P1),那么称M是X-丁投射模.本文证明了X-丁投射模类是投射可解的并且X-丁投射模保持直和项和直和.进而引入了X-丁投射维数的定义并给出了X-丁投射维数有限的等价刻画以及其他相关性质.证明了若环R的整体X-丁投射维数有限,则(X-DP(R),(X-DP(R))⊥)是完备遗传余挠对.

定义1[4]如果存在正合列P=∶…→P1→P0→P0→P1→…,其中Pi,Pi是投射模,i∈Z,对于任意平坦模F,HomR(-,F)作用在正合列P上保持正合,并且M=Ker(P0→P1),那么称M是丁投射模.在这种情况下,称正合列P为强完全零调复形.

定义2[3]设X是包含所有投射模的R-模类.如果存在正合列

P=∶…→P1→P0→P0→P1→…

其中Pi,Pi是投射模,i∈Z,对于任意R-模P∈X,HomR(-,P)作用在正合列P上保持正合,并且M=Ker(P0→P1),那么称M是X-Gorenstein投射模. 在这种情况下,称正合列P为X-完全零调复形.

引理1[5](Horse Lemma) 设X是R-模类,且X对有限直和封闭.设0→M′→M→M″→0是R-模短正合列并且对于任意R-模Y∈X,HomR(-,Y)作用在短正合列上保持正合.若M′和M″有余真右X-分解,则M也有余真右X-分解.

定义3[6]称R-模类X是投射可解的,若P(R)⊆X,且对任意短正合列0→X′→C→X″→0,其中X″∈X,则X′∈X当且仅当C∈X.

定理1[6](Eilenberg’s swindle)若R-模类X是投射可解的且对可数直和封闭,或是内射可解的且对可数直积封闭,则R-模类X对直和项封闭.

定义4[7]设C是R-模范畴的子范畴.

定义5[7]设A,B是R-模类.若A=⊥B且B=A⊥,则称C=(A,B)是余挠对.

定义7[7]设(A,B)是余挠对.若满足下面等价条件的任意一个:

1) 对任意R-模M,存在正合列0→M→Y→L→0,其中Y∈B,L∈A.

2) 对任意R-模M,存在正合列0→D→C→M→0,其中C∈A,D∈B.则称余挠对(A,B)是完备的.

定义8设X是包含所有平坦模的R-模类.如果存在正合列P=∶…→P1→P0→P0→P1→…,其中Pi,Pi是投射模,i∈Z,对于任意R-模F∈X,HomR(-,F)作用在正合列P上保持正合,并且M=Ker(P0→P1),那么称M是X-丁投射模.在这种情况下,称正合列P为X-强完全零调复形.记X-DP(R)为X-丁投射模类.

定理2设M是右R-模.则下列条件等价:

1)M是X-丁投射模;

2)M满足以下两个条件:

② 存在正合列0→M→P0→P1→…,其中Pi是投射模,i≥0且为整数,对任意R-模F∈X,HomR(-,F)作用在正合列上保持正合.

3) 存在正合列0→M→P→G→0,其中P是投射模,G是X-丁投射模.

证明1)⟺2)、1)⟹3)由X-丁投射模定义可得.

3)⟹2) 设任意R-模F∈X.用HomR(-,F)作用于短正合列0→M→P→G→0,由长正合序列定理有

定理31) 投射模是X-丁投射模,X-丁投射模是丁投射模.

2) 若X是平坦模类,则X-丁投射模和丁投射模一致.

3) 若X是丁投射模类,则任意X-丁投射模是投射模.

2) 显然.

推论1任意的R-模M是投射的当且仅当M是X-丁投射模且M∈X.

证明: 由定理3可证.

推论2对于任意的结合环R,下列条件等价:

1)X是投射模类.

2) 对于任意R-模F,F是X-丁投射模.

证明由定理3可证.

引理2设0→A→B→C→0是短正合列.若A,C是X-丁投射模,则B是X-丁投射模.

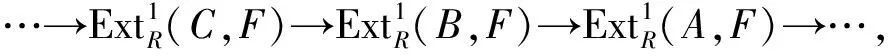
定理4X-丁投射模类是投射可解的.

证明设0→A→B→C→0是短正合列,其中C是X-丁投射模.只需证明A是X-丁投射模当且仅当B是X-丁投射模.若A是X-丁投射模,由引理2知B是X-丁投射模.若B是X-丁投射模,由X-丁投射模定义知,存在短正合列0→B→P→N→0,其中N是X-丁投射模,P是投射模.考虑交换图,如图1所示.

图1 交换图Fig.1 Commutative diagram

因为C和N是X-丁投射模,由引理2知,L是X-丁投射模.对于短正合列0→A→P→L→0,由P是投射模和X-丁投射模的定义知A是X-丁投射模.

推论3X-丁投射模类对直和与直和项封闭.

证明由X-丁投射模定义,X-丁投射模对直和封闭.因为X-丁投射模类是投射可解的,所以由定理1知X-丁投射模对直和项封闭.

充分性) 由M,N是X-丁投射模知存在正合列

A=∶0→M→P0→P1→…

B=∶0→N→Q0→Q1→…

其中Pi,Qi均为投射模,i∈Z,用HomR(-,F)作用保持正合.存在同态f:M→N和同态Pi→Qi,考虑交换图，如图2所示.

图2 交换图Fig.2 Commutative diagram

考虑交换图，如图3所示.

图3 交换图Fig.3 Commutative diagram

图4 交换图Fig.4 Commutative diagram

其中K=Coker(M→N⊕P0).令

D=∶0→M→M→0→…

C=∶0→M→N⊕P0→Q0⊕P1→…
L=∶0→K→Q0⊕P1→…

则存在正合列0→D→C→L→0,其中复形D,C正合,从而复形L正合,且HomR(-,F)作用L上保持正合,其中F∈X.因为有正合列0→M→N⊕P0→K→0,0→M→N→L→0,所以存在同态h:K→L使交换图如图5所示.

图5 交换图Fig.5 Commutative diagram

引理3若存在正合列0→Kn→Gn-1→…→G0→M→0,其中G0,…,Gn-1是X-丁投射模,则对任意平坦维数有限R-模A,有

其中:i>0且为整数.

证明将长正合列打断成一系列短正合列,如下:

A=∶0→C1→G0→M→0

其中C1=Ker(G0→M)

B=∶0→C2→G1→C1→0

其中C2=Ker(G1→G0)

…

X=∶ 0→Kn→Gn-1→Cn-1→0

其中Cn-1=Ker(Gn-2→Gn-3)

用HomR(-,F)作用于长正合列X,对任意平坦维数有限R-模F,由长正合列定理可得

又因为G0,…,Gn-1是X-丁投射模,所以

定义9若存在正合列0→Gn→Gn-1→…→G0→M→0,其中:G0,…,Gn是X-丁投射模,则称R-模M的X-丁投射维数小于等于n.用X-DpdR(M)表示R-模M的X-丁投射维数.

称GX-Dpd(R)为环R上的整体X-丁投射维数,记

引理4M是任意R-模,考虑下面两个正合列:

A=∶0→Ln→Xn-1→…→X0→M→0

证明设Ln是X-丁投射模.取R-模M的投射分解

P1→P0→M→0

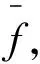
图6 交换图Fig.6 Commutative diagram

考虑交换图，如图7所示.

图7 交换图Fig.7 Commutative diagram

0→K→Pn-1⊕Ln→…→

P0⊕X1→X0→0

其中X0是X-丁投射模.由于X-丁投射模对直和与直和项封闭,所以Pn-1⊕Ln与Xi⊕Pi-1是X-丁投射模,i=1,…,n-1.因为X-丁投射模类是投射可解的,所以K是X-丁投射模.类似有正合列

定理6设0→K→G→M→0是短正合序列,其中G是X-丁投射模.若M是X-丁投射模,则K是X-丁投射模.否则

X-DpdR(K)=X-DpdR(M)-1≥0

证明对于短正合列0→K→G→M→0,若M是X-丁投射模,因为X-丁投射模类是投射可解的,所以K是X-丁投射模.

若M不是X-丁投射模,设M的X-丁投射维数为m,则M有X-丁投射分解分解:

0→Xm→Xm-1→…→X1→X0→M→0

其中X0,…,Xm是X-丁投射模.对K作投射分解,有…→Pm-1→Pm-2→…→P1→P0→K→0,其中Pi是投射模,i≥0且为整数.存在正合列0→I→Pm-2→…→P0→K→0,其中I=Im(Pm-1→Pm-2).所以有正合列0→I→Pm-2→…→P0→G→M→0.由引理4可知I是X-丁投射模,此时X-DpdR(K)≤m-1.若X-DpdR(K)

X-DpdR(K)=m-1=X-Dpd(M)-1

命题1设R-模M的X-丁投射维数有限,n是整数.下列条件等价:

1)X-DpdR(M)≤n;

4) 若存在正合列0→Kn→Gn-1→…→G0→M→0,其中Gi是X-丁投射模,则Kn也是X-丁投射模.

进而,X-DpdR(M)可由下列公式计算:

2)⟹3) 显然.

A=∶0→C′1→G′0→Kn→0

其中C′1=Ker(G′0→Kn)

B=∶0→C′2→G′1→C′1→0

其中C′2=Ker(G′1→G′0)

…

X=∶0→G′m→G′m-1→C′m-1→0

其中C′m-1=Ker(G′m-2→G′m-3)

对于任意平坦模F,用HomR(-,F)分别作用短正合列A,…,X,再由长正合序列定理有

其中m>0且为整数.由维数推移公式可知,

从而

故

由定理5知C′1,…,C′m-1,Kn是X-丁投射模.

4)⟹1) 因为Kn是X-丁投射模,所以

X-DpdR(M)≤n

结论得证.

定理7设M是具有有限X-丁投射维数的R-模,且X-DpdR(M)=n,则M存在满的X-丁投射预覆盖φ:G→M.记K=Kerφ,则pdRK=n-1.

证明因为X-DpdR(M)=n,所以存在正合列0→Cn→…→C0→M→0,其中Ci是X-丁投射模,0≤i≤n.对M作投射分解,存在正合列

其中K′=Kerdn-1,Pi是投射模,0≤i≤n-1.由引理4可知,K′是X-丁投射模.根据X-丁投射模定义,存在零调复形

…→Q-1→Q0→Q1→…→Qn-1→Qn→…

使得有正合列0→K′→Q0→Q1→…→Qn-1→G→0,其中G是X-丁投射模,Qi是投射模,其中i>0且是整数.对任意R-模F∈X,用HomR(-,F)作用保持正合.因此存在同态Qi→Pn-1-i,0≤i≤n-1,和同态f:G→M,交换图如图8所示.

图8 交换图Fig.8 Commutative diagram

于是可诱导出复形的链映射,如图9所示.

图9 交换图Fig.9 Commutative diagram

0→HomR(C′,K)→HomR(C′,P0⊕G)

并且HomR(C′,φ)是满的,即φ是M的X-丁投射预覆盖.

推论4设M是具有有限X-丁投射维数的R-模,且X-DpdR(M)=n.若存在短正合列0→M→H→G→0使得pdR(H)=n,则G是X-丁投射模.

证明对n分类讨论,有以下情形:

若n=0,即X-DpdR(M)=0,则M是X-丁投射模,由X-丁投射模定义,必然存在短正合列0→M→H→G→0,其中H是投射模,所以pdR(H)=0.

若n>0,由定理7,存在短正合列0→K→G′→M→0,其中G′是X-丁投射模,K=Ker(G′→M)且pdR(K)=n-1.对于X-丁投射模G′,存在短正合列0→G′→P→G→0,其中P是投射模,G是X-丁投射模.考虑交换图，如图10所示.

图10 交换图Fig.10 Commutative diagram

因为pdR(K)=n-1,且P是投射模,所以pdR(H)≤n.

若n=1,pdR(K)=n-1=0,则K是投射模,因此pdR(H)=1.否则pdR(H)=0,则H是投射模即为X-丁投射模,又因为G是X-丁投射模,由X-丁投射模类是投射可解的,所以M是X-丁投射模,矛盾.

若n>1,对于短正合列0→K→P→H→0,pdR(H)=pdR(K)+1=n.

命题2对任意R-模M和M′,

证明设X-DpdR(M)=m,X-DpdR(M′)=n,其中m,n均是整数且m

将上述两个正合列作直和可得正合列

0→Gn′→…→Gm⊕G′m→…→

G0⊕G0′→M⊕M′→0

由于X-丁投射模类对直和封闭,所以G0⊕G′0,…,Gm⊕G′m是X-丁投射模.因此,

X-DpdR(M⊕M′)=n

设M′是N的直和项,只需证明X-DpdR(M′)≤X-DpdR(N)即可.设X-DpdR(N)=n.对n进行归纳假设:当n=0时,由于X-丁投射模保持直和项封闭,所以N是X-丁投射模.当n>0时,设N=M⊕M′,选取正合列

0→K′→G′→M′→0,0→K″→G″→M→0

其中G′,G″是投射模,K′=Ker(G′→M′),K″=Ker(G″→M).则有下列交换图,如图11所示.

图11 交换图Fig.11 Commutative diagram

由同调代数基本定理知,序列0→K′⊕K″→G′⊕G″→N→0正合.因为X-DpdR(N)=n>0,所以N不是X-丁投射模.由定理6可知:

X-DpdR(K′⊕K″)=X-DpdR(M)-1=n-1

因此,由假设归纳,X-DpdR(K′)≤n-1.又因为短正合列0→K′→G′→M′→0中G′是X-丁投射模,所以X-DpdR(M′)≤n.从而

X-DpdR(M′)≤X-DpdR(N)

结论得证.

命题3设0→A→B→C→0是短正合序列,若A,B,C中任意两个X-丁投射维数有限,则第三个也有限.

证明1) 若X-DpdR(A)≤n,X-DpdR(C)≤m,m≤n.由命题1,对任意平坦模Q,有

用HomR(-,Q)作用正合列0→A→B→C→0,由长正合序列定理,有

2) 若X-DpdR(A)≤n,X-DpdR(B)≤m,m≤n.

3) 或X-DpdR(B)≤n,X-DpdR(C)≤m,m≤n.

2)、3)证明类似于1),分别可知C与A的X-丁投射维数有限.结论得证.

定理8若GX-Dpd(R)<∞,则(X-DP(R),(X-DP(R))⊥)是完备遗传余挠对.

因此,(X-DP(R),(X-DP(R))⊥)是遗传余挠对.对于正合列0→K→G→M→0,其中K∈(X-DP(R))⊥,G是X-丁投射模.由完备余挠对定义,(X-DP(R),(X-DP(R))⊥)是完备遗传余挠对.