关于极大P-投射模及其投射维数

于梅菊，刘楠楠

(通化师范学院 数学学院，吉林 通化 134000)



关于极大P-投射模及其投射维数

于梅菊，刘楠楠

(通化师范学院 数学学院，吉林 通化 134000)

该文在极大P-内射模的基础上构造出了它的对偶模极大P-投射模，引入了极大P-投射维数的概念，并且研究了极大P-投射模及其投射维数的等价命题及其性质.

极大P-投射模；极大P-投射维数;极大P-左半单环

环上的模是向量空间的推广,最常用也是最基本的三大模类是投射模、内射模、平坦模.由于投射模是自由模的自然推广,而且投射模在对各种环如半单环、V环、完全环等的刻画上起了很大的作用,正如利用Bear准则对内射模进行延拓一样,人们对投射模也进行了相应的延拓,例如文献[1-4]分别构造了P-投射模，FP-投射模、极大投射模、n-P投射模并且研究了它们的性质.所构造出的新模,不仅保有了原投射模的一些良好的性质,而且利用它们可以更好地刻画环的性质,研究环的结构.本文受文献[5]的启发,定义了极大P-投射模,借助它进一步构造了极大P-投射维数和极大P-左半单环，并且刻画了它们的性质.

本文所讨论的环都是带有单位元且存在极大左主理想的结合环，模指酉模.

1 极大P-投射模

定义1 若对R的每个极大左主理想I,及任意左R-模同态f∈HomR(M,R/I),都存在左R-模同态g∈HomR(M,R),使得图1可交换,即f=πg,则称左R-模M为左极大P-投射模,简称极大P-投射模.

显然,自由模、投射模⟹P-投射模⟹极大P-投射模.

图1 交换图

由定义可以得到下面三条性质

命题1 设R是任意环,M是任意左R-模,则下列条件等价:

(1)M是极大P-投射模;

(2)对任意左R-模正合列0→I→R→R/I→0,其中I是R的极大左主理想,有正合列0→HomR(M,I)→HomR(M,R)→HomR(M,R/I)→0;

证明 (1)⟺(2)M是极大P-投射模⟺对R的每个极大左主理想I,任意左R-模同态f∈HomR(M,R/I),都存在左R-模同态g∈HomR(M,R),使得f=πg,即HomR(M,-)保持满同态,则有0→HomR(M,I)→HomR(M，R)→HomR(M,R/I)→0正合.

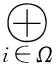
命题3 对任意左R-模正合列0→N1→N→N2→0,下列结论成立：

(1)若左R-模N1,N2为极大P-投射模,则左R-模N也为极大P-投射模;

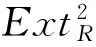
证明 (1)对左R-模正合列0→N1→N→N2→0,使用长正合列定理可得

0→HomR(N2,I)→HomR(N,I)→HomR(N1,I)→

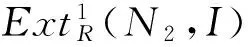
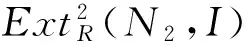
定义2 环R是V环,如果环R的每个单左R-模都是内射模.

定义3 环R是左主理想环，如果环R的每一个左理想都是主理想，而且没有零因子.

定理1 若R既是左主理想环又是V环,则对R的任意理想E是极大P-投射模.

证明 设I是环R的极大左主理想,对于任意的f∈HomR(E,R/I),由于R是左主理想环,所以有R/I是单模,又因为R是V环,所以有R/I是内射模,则一定存在g∈HomR(R,R/I),使得f=gi,由于R是投射模,所以存在h∈End(R),使得g=πh(π为自然投射),如图2所示,因此有f=gi=πhi,即E是极大P-投射模.

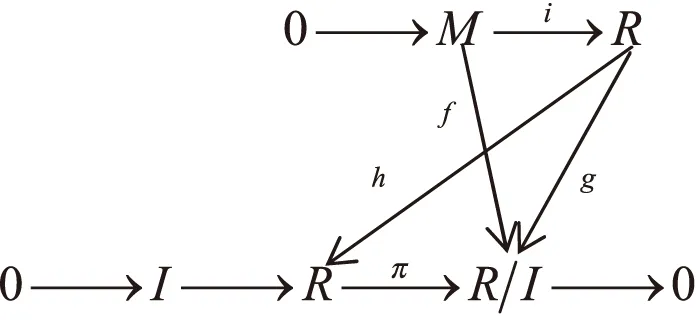
图2 交换图

定义4 若每个左R-模M都是极大P-投射模,则称环R是极大P-左半单环.

定理2 R是环,则以下命题等价：

(1)R是极大P-左半单环;

(2)每个极大P-投射模的商模是极大P-投射模;

(3)每个P-投射模的商模是极大P-投射模;

(4)每个投射模的商模是极大P-投射模.

证明 (1)⟹(2)由于R是极大P-左半单环,因此每个左R-模都是极大P-投射模,故每个极大P-投射模的商模也是极大P-投射模；(2)⟹(3)⟹(4)显然；(4)⟹(1)设M是任意左R-模,由于任何左R-模都是某个一个投射模的同态像，所以存在投射模P,有正合列P→M→0,由(4)可知M是极大P-投射模,因此R是极大P-左半单环.

2 极大P-投射模维数

由于每个模都是某一个投射模的同态像[7]，所以每个左R-模M都有投射分解,而投射模是极大P-投射模,所以每个左R-模M都存在极大P-投射模分解,即存在正合列…→Pn→Pn-1→…→P1→

P0→M→0，其中每个Pn都是极大P-投射模.

定义5 左R-模M的极大P-投射维数定义为

min{n/存在M的一个极大P-投射分解…→0→Pn→Pn-1→…→P1→P0→M→0}记作max.pd(M).若上述的n不存在,则max.pd(M)=∞.

显然对任意左R-模M,有max.pd(M)≤pd(M).

命题4 若左R-模M是极大P-投射模当且仅当max.pd(M)=0.

证明 因为M是极大P-投射模,则M有极大P-投射分解0→…→0→F0→M→0,其中F0=M,Fi=0(i≥i),那么max.pd(M)=0;反之设max.pd(M)=0,则M有一个极大P-投射分解0→…→0→F0→M→0,其中Fi=0(i≥i),因此F0≅M,故M是极大P-投射模.

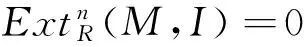
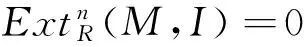
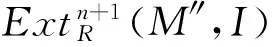
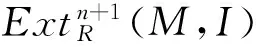
命题7设M是任意左R-模,则下列条件是等价的:

(1)max.pd(M)≤1；

(2)极大P-投射模的子模是极大P-投射模；

(3)有极大P-投射模F0,F1,使M≅F0/F1.

证明 (1)⟹(2)设P0是极大P-投射模,P1是P0的子模,则有正合列0→P1→P0→P0/P1→0,由于对任意左R-模M,有max.pd(M)≤1,所以max.pd(P0/P1)≤1,则P1是极大P-投射模.

(2)⟹(1)设M是任意右R-模,则存在自由模F0,使正合列0→F1→F0→M→0成立,因为F0是极大P-投射模,由条件(2)可知F1也是极大P-投射模,则有max.fd(M)≤1.

(1)⟺(3)显然.

命题8 设M是左R-模,则下列条件等价

(1)max.pd(M)≤n；

(2)⟹(3)显然；

[1]苗佳晶.关于P-投射模[J].吉林师范大学学报,2007(3):109-110.

[2]黄影.关于FP-投射模[J].吉林师范大学学报,2007(1):47-48.

[3]罗荣.关于极大投射模[J].四川师范大学学报,2005,28(4):405-408.

[4]乔虎生,汪涛.n_P投射模与强P-投射模[J].西北师范大学学报,2013,49(2):23-27.

[5]胡筱鸥.极大P-内射模[J].商丘师范学院学报,2008,24(12):46-48.

[6]Rotman J J. An Introduction to Homological Algebra[M].New York:Acad.Press,1979.

[7]周伯勋.同调代数[M].北京:科学出版社,1988.

(责任编辑:陈衍峰)

10.13877/j.cnki.cn22-1284.2016.08.010

2016-03-20

通化师范学院校级立项“关于内射模和平坦模的研究”(201264)

于梅菊,女，吉林集安人,博士,讲师．

O153

A

1008-7974(2016)04-0032-03