一类推广的薛定谔—泊松系统的可解性*

丁 凌，庄常陵

(湖北文理学院数学与计算机科学学院，湖北襄阳441053)

1 背景和主要结论

考虑下面具有临界非线性项的一类推广的薛定谔-泊松系统:

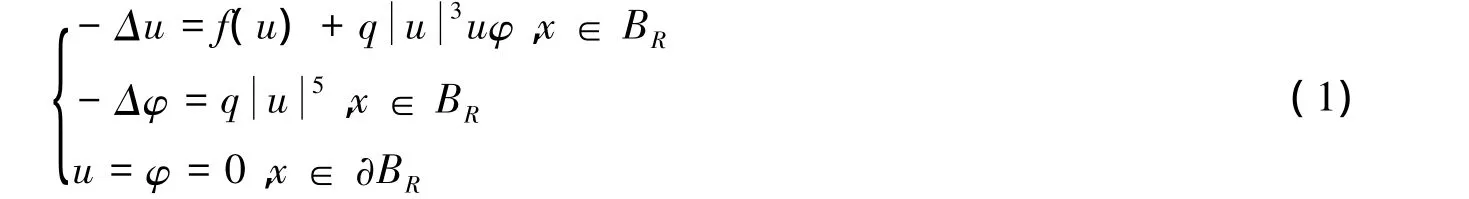
其中q＞0，BR是R3中具以0点为球心，以R＞0为半径的球.f满足如下的条件:

系统(1)来源于物理里的经典模型，由Schro..dinger方程和Poisson方程耦合的系统(1)描述了带电粒子在电磁场的相互作用［1］.特别在寻找静电类的解时就必须解系统(1).根据量子力学里的数学公式知道，当质量为m电荷为q的粒子在具有向量势A(x，t)和数量势φ(x，t)的作用下运动，其波函数ψ(x，t)满足下面的 Schro..dinge 类方程:

这里i是虚单位，ħ是 Planck常数，c是光在真空里的速度，g是 Gauge不变函数.方程(3)的右边表示向量的数量积，即

用文献［1-3］同样的观点，考虑带电粒子在自身的电磁场里的相互作用.假定电磁场不是给定的，这样不得不解一个未知函数为粒子的波函数和与波函数相关势函数A，φ的系统，电磁场的势函数由下面Maxwell的方程给定:

定理1 假定q＞0和(f1)-(f4)成立，则系统(1)有一个正解.

注记1 定理1的一类推广的薛定谔-泊松正解的存在性结论.文献［4］只研究了线性情况，即f(s)=s;文献［5］只研究了次临界及q＞0的情况.此处的研究是对文献［4］中研究的问题和结果的推广和补充.

用 ·p表示Lp范数表示)的范数，φ1(x)＞0表示λ1的特征函数，用Ci(i=1，2，…)表示不同的正常数.

2 主要结果的证明

显然，(u，φ)是系统(1)的弱解当且仅当(u，φ)是J在)上的临界点.另外泛函J是强无界的(下方无界或者上方无界)，但根据文献［1］介绍的思想可以克服这一困难.那就是对于每一个)，用Φ(u)∈)表示问题(5)的唯一解:

引理1 假定f满足(f1)-(f4)，则

证明 1)根据(f1)-(f2)，对任意 ε＞0和r∈(1，5)，存在C=C(ε)＞0使得对任意的s∈，有

从式(9)可知，存在一个充分小ρ和a＞0，使得对所有的满足u∈)，u=ρ的u成立.

2)因为在BR(0)上的特征函数φ1(x)＞0，对t＞0且t→+∞，再根据式(6)和(f4)可得

取 e=tφ1，令 T 充分大，当 t＞T 使得 e ＞ρ且 I(e)＜0.证毕.

从引理1可以看出泛函满足山路定理的几何结构［6］，故存在一个(PS)序列{un}满足

其中 c=infγ∈Γmax0≤γ≤1I(γ(τ))，Γ={γ∈C(［0，1］)):γ(0)=0，γ(1)=e}是连接 0 到 e的连续路径.

定理1的证明 首先证明(PS)序列{un}是有界序列.根据(f3)和(f4)可得βs2≤2F(s)≤f(s)s.于是有

其次证明系统(1)有一个正解.由上面知序列{un}有界，存在着一个弱收敛的子列仍然记为{un}收敛到u.下面证明u≢0，用反证法.如果u≢0，则于)，故有un→0于Lp(BR)(P∈［2，6)).根据(f1)-(f3)，∫BRf(un)und x→0 和∫BRF(un)d x→0.因为{un}是(PS)序列，所以有

与式(12)相矛盾.所以u≢0.

故 u-=0，于是u=u+≥0.由最大值定理可得u是系统(1)的正解.

［1］BENCI V，FORTUNATO D.An Eigenvalue Problem for the-Maxwell Equations［J］.Topol Methods Nonlinear Anal，1998(11):283-293

［2］ APRILE T D，MUGNAI D.Existence of Solitary Waves for the Nonlinear Klein-Koedon-Maxwell and-Maxwell Equations［J］.Proc Roy Soc Edinburgh Sect A，2004(134):893-906

［3］APRILE T D，WEI J C.On Bound States Concentrating on Spheres for the MaxwellEquations［J］.SIAM J Math Anal，2005(37):321-342

［4］AZZOLLINI A，D’AVENIA P.On a System Involving a critically Growing Nonlinearity［J］.J Math Anal Appl，2012(387):433-438

［5］AZZOLLINI A，D’AVENIA P，LUISI V.GeneralizedPoisson Type Systems［J］.Communications on Pure and Appllied Analysis，2013(12):807-879

［6］AMBROSETTI A，RABINOWITZ P H.Dual Variational Methods in Critical Point Theory and Applications［J］.J Funct Anal，1973(14):349-381

［7］BREZISH，NIRENBERG L.Positive Solution of Nonlinear Elliptic Problems Involving Critical Sobolevexponent［J］.Comm Pure Appl Math，1983(36):437-477