二维连续型随机变量变换的概率分布*

陶 宝，袁德美

(重庆工商大学数学与统计学院，重庆400067)

设(X，Y)是二维连续型随机变量，联合概率密度已知，若存在二元函数u=g(x，y)，称U=g(X，Y)为二维连续型随机变量(X，Y)的函数.文献［1］和［2］讨论了U=g(X，Y)的概率密度公式及计算.若还存在二元函数v=h(x，y)，称)为二维连续型随机变量 (X，Y)的变换.如何求二维随机变量(U，V)的联合概率密度，文献［3-5］进行了简单的讨论.基于文献［5］此处研究了二维连续型随机变量在平面R2上的一对一变换的概率分布，还研究了若平面R2被分成若干区域，分区域成一对一变换时的概率分布.

定理1 设(X，Y)的联合概率密度为 fX，Y(x ，y)，变换

设 U=g(X，Y)，V=h(X，Y)，则(U，V)的联合概率密度为

证明 (U，V)的联合分布函数:

作积分变换(1)得

对式(2)两边关于s，t求二阶混合偏导数，得 (U，V)的联合概率密度(将s，t分别改为u，v)为

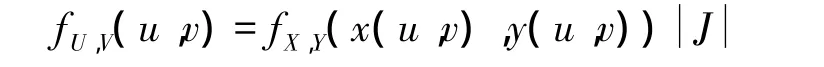
由定理1容易得到以下推论.

推论 1 设(X，Y)的联合概率密度为 fX，Y(x，y)，若 U=aX+b，V=cY+d，其中 a，c为非零常数，则(U，V)的联合概率密度为

定理1只考虑了整个平面R2上的一对一变换，若平面R2被分成若干区域，下面讨论当分区域成一对一变换时的变量变换法.

定理 2 设(X，Y)的联合概率密度为 fX，Y(x，y)，A0，A1，A2，…，An是 R2的一个划分，且 A0满足 P((X，Y)∈A0)=0(A0可能是空集)，若变换

在每个区域Ai上有连续偏导数，且存在唯一的逆变换

证明 (U，V)的联合分布函数

式(6)两边关于s，t求混合二阶偏导，并将s，t分别改记为u，v，就得到式(4).注意，如果每个区域Ai上逆变换相同，那么B1，B2，…，Bn两两互不相交，从而定理2回到定理1.

关于相互独立的正态随机变量的和、差、积的概率分布，大学概率统计教材讨论了很多，而相互独立的正态随机变量的商的概率分布可以利用定理2求得，下面只讨论标准正态变量的情形.

定理3 若随机变量X与Y独立同标准正态分布，记U=X/Y，则U服从柯西分布，即相互独立的标准正态变量之商是柯西随机变量.

由于点(x，y)和(－x，－y)映射至同一点(u，v)，所以该变换不是一对一变换，而是多对一变换.

记 A0={(x，y):y=0}，A1={(x，y):y＞0}，A2={(x，y):y＜0}，显然 A0，A1，A2是 R2的一个划分，并且P((X，Y)∈A0)=P(Y=0)=0.

即U服从柯西分布.

［1］刘平兵.二维连续型随机变量函数的密度公式及计算［J］.数学理论与应用，2005，25(4):94-96

［2］袁德美，安军，陶宝.概率论与数理统计［M］.北京:高等教育出版社，2011

［3］张洪川，盛克敏，马丽琼.一维与二维连续随机变量的函数的分布［J］.西南民族大学学报:自然科学版，2005，31(6):995-997

［4］余本国.一般二维连续型随机变量函数分布的讨论［J］.华北工学院学报，2004，25(2):94-96

［5］茆诗松，程依明，濮晓龙.概率论与与数理统计教程［M］.北京:高等教育出版社，2011