逆极限空间转移映射非游荡集的中心测度*

贺 毅，张 君，白丹莹

(重庆师范大学数学学院，重庆401331)

若X为紧致度量空间，f:X→X连续，X的逆极限空间为形如=(x0，x1，x2，…)的点构成的集合，其中f(xi+1)=xi，i≥0.引入度量，其中d为X上的度量.用，f)表示X的逆极限空间.转移映射σ:(X，f)→(X，f)定义为 σ(x0，x1，x2，…)=(f(x0)，x1，x2，…)，注意这里 σ 与单边符号空间的转移映射不同，显然σ是同胚.投射)→X定义是 πi(x0，x1，x2，…)=xi，i=0，1，2，…，f)的拓扑由D诱导且(X，f)是紧致的.

1992年，周作领在文献［1］中讨论了弱几乎周期点和测度中心;1995年，顾荣宝在文献［2］中讨论了逆极限空间上的移位映射的混沌性;1998年马东魁在文献［3］中讨论了Schweizer－Smital混沌与测度的关系.此处在前人的基础上对非游荡点集和强非游荡点集进行讨论，主要讨论了非游荡点和强非游荡点在逆极限转移映射的性质.文中出现与这些概念相关符号及记法分别与上述对应的文献相同.

定理1［3］若f:X→X连续，则M(σ)=(M(X)，f).

1 基本概念

定义1 设X是紧致度量空间，点x∈X称为f的非游荡点，如果对∀ε＞0，∃n∈N+，∃y使得d(x，y)＜ε，有 d(f(y)，x)＜ε.f的全体非游荡点组成的集合记 Ω(f).

定义2 称x∈X为f的强非游荡点，如果对∀ε＞0存在y∈X，使得

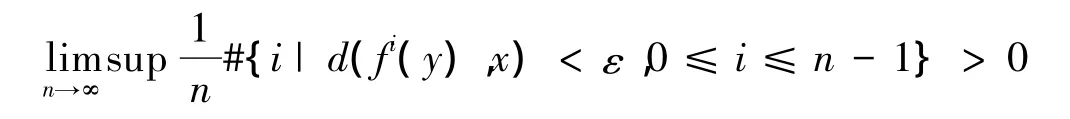
这里#{·}表示集合的基数.f的强非游荡点集合也叫强非游荡集，记作SΩ(f).

2 主要结果

引理1若f:X→X为连续满射，则Ω(σf)={Ω(f)，f}.

证明 结合定义1定理1立即可证.

定理4 若f|M(f):M(f)→M(f)是强非游荡集，当且仅当σ|M(σ):M(σ)→M(σ)是强非游荡集.

证明 按照定理3的方式可以证明定理4.

［1］周作领.弱几乎周期点与中心测度［J］.中国科学(A辑)，1992(6):572-581

［2］顾荣宝.逆极限空间上移位映射的拓扑熵与混沌［J］.武汉大学学报:自然科学版，1995，41(2):22-26

［3］马东魁.关于逆极限空间转移映射的性质［J］.中山大学:自然科学版，1997，37(2)37-42

［4］廖公夫，王立冬，范钦杰.映射迭代与混沌动力系统［M］.北京:科学出版社，2013