有极小理想的半环

何 鹏, 舒乾宇(四川师范大学 数学与软件科学学院, 四川 成都 610066)



有极小理想的半环

何 鹏, 舒乾宇*
(四川师范大学 数学与软件科学学院, 四川 成都 610066)

首先讨论了半环中极小理想的存在性问题,给出了极小理想存在的一些充要条件,其次给出了极小理想的一些特征,最后描述了有极小理想的半环的结构.

半环; 极小理想; Wedderburn结构

1 引言及预备知识

1934年,H. S. Vandiver[1]引入了半环的概念,作为对环和分配格概念的一种推广,半环被广泛的应用于分析学、拓扑学以及非交换环论等数学学科,还被广泛应用于自动机理论、语言理论、选择理论和其它一些应用数学的分支[2-8].同时,半环作为重要的代数工具也被广泛应用于计算机科学技术、代数编码理论[4-5,7].

理想在半环的结构中起着非常重要的作用,许多研究者[9-10]都曾讨论过半环上理想的相关性质.然而这些性质与通常环中理想的性质却不一致[11-12],于是研究者们加强了条件,以期能得到一些和环上类似的结果[13-14].尽管如此,结果仍然不如人意.半环中所有理想连同半环本身构成一个格,称为理想格,理想格中都有极大元,也就是说任意半环都有极大理想.实际上,极大理想在素理想和半环结构的刻画中都起着非常重要的作用[15].一个很自然的问题是在理想格中是否有极小元,也就是每个半环是否有极小理想?极小理想又有些什么样的性质?本文将首先讨论半环上极小理想的存在性问题以及极小理想的相关性质,最后将刻画有极小理想的半环的结构.

定义 1.1[16]设L是一个非空集合,若在L上有2个代数运算“+”和“·”,使得下列条件成立:

1) (L,+,0)是交换幺半群；

2) (L,·,1)是幺半群；

3) 对任意a,b,r∈L,r·(a+b)=r·a+r·b,(a+b)·r=a·r+b·r;

4) 对任意r∈L,0·r=r·0=0;

5) 0≠1,

则称L=〈L,+,·,0,1〉为半环.

特别地,若对任意的r,r′∈L,都有r·r′=r′·r,则称L为交换半环.对任意的a,b∈L,若由a+b=0蕴含a=b=0,则称半环L是Zerosumfree的.为方便起见,在不引起混淆的前提下,以下用ab代替a·b.

定义 1.2[16]1) 半环L上的一个非空集合I称为L的左理想,若I满足以下条件:

(i) 若a,b∈I,则a+b∈I;

(ii) 若a∈I,r∈L,则ra∈I;

(iii)I≠L.

类似地,可以定义L的右理想.既是左理想又是右理想就称为L的理想.

2) 设I≠{0}是L的(左,右)理想.如果除了{0}和它自身外,I不再包含其他任何理想,则称I是L的极小(左,右)理想.

3) 设I≠{0}是L的(左,右)理想.如果I不包含于L的任意理想中,则称I是L的极大(左,右)理想.

例 1.1 在半环L=〈N∪{∞},+,·,0,1〉中,I={0,∞}即为L的极小理想,其中,N表示自然数集,+和·分别表示整数的普通加法和乘法运算.

例 1.2 理想I={0,1}是半环L=〈N∪{∞},+,·,0,∞〉的唯一极小理想,其中,对任意的a,b∈N∪{∞}都有a+b=max{a,b},a·b=min{a,b}.

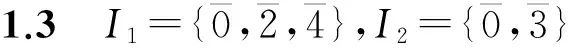
例 1.4 设L=〈L,+,·,0,1〉是布尔半环且S=Mn(L),其中L={0,1},则有

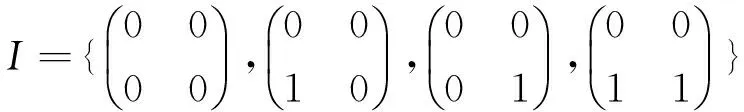
是L的极小右理想.

设I1、I2和I都是半环L的理想.定义集合

I1I2={aibi|ai∈I1,bi∈I2}

与

I1+I2={ai+bi|ai∈I1,bi∈I2}

分别称为理想I1与I2的积与和.特别地,对任意的a∈L,{a}I简记为aI.如果I1∩I2={0},则I1与I2的和称为直和,记作I1+I2=I1⊕I2.

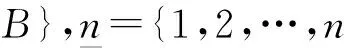
注 1.1 设L是半环且ideal(L)={I|I是L的理想}∪L,则(ideal(L),+,∩)是完备格,称为理想格.然而值得注意的是,即使L是交换半环,这个格也不一定是模格.例如在例1.1所指的半环L=〈N∪{∞},+,·,0,1〉中,I1=2N{2},I2=2N,I3=N{1,2,5},I4=N{1,2},I5=N{1}都是集合ideal(N)中元素,且I1⊆I2⊆I5,I1⊆I3⊆I4⊆I5.因此(ideal(L),+,∩)不是模格.

定义 1.3[12]设H1⊇H2⊇…⊇Hn⊇…是半环L中的一理想降链.若存在正整数n0使得Hn0=Hn0+1=…,则称该降链是稳定的.

定义 1.4[16]设L=〈L,+,·,0,1〉为半环,

1) 对任意的r∈L{0},如果存在a∈L{0}使得ar=ra=a,则称a是乘法吸收元;

2) 设a、b是L中的2个非零元,如果ab=0,则称a是L的左零因子,b是L的右零因子.既是左零因子又是右零因子的元称为零因子.不含零因子的半环L称为整半环;

3) 设a是L中的非零元,若存在b∈L使得a=aba,则称a是乘法正则的.若L中任意元都是乘法正则的,则称半环L是乘法正则的;

4) 设a∈L,若存在正整数m使得am=0,则称a是幂零元,使得am=0成立的最小的正整数m称为元素a的幂零指数.

定义 1.5[16]设I是半环L的理想.若存在元素a∈L使得I=〈a〉,则称I是L的主理想,a为I的生成元,其中

}.

若L是交换半环,则〈a〉={ra|r∈L}.设S是非空子集,则集合

表示由S生成的理想.

定义 1.6 设I是半环L的理想,

1) 对任意的a,b∈L,若a∈I且a+b∈I蕴含b∈I,则称I是半负的.不包含半负理想的半环L称为Austere的[16];

2) 若存在理想H使得I+H=L且I∩H={0},则称H是I的补理想[16];

3) 若存在正整数m使得Im={0},则称I是幂零的.使得Im={0}成立的最小正整数m称为I的幂零指数;

4) 若I2=I,则称I是幂等的.

定义 1.7[17]设e是半环L中的任意非零元.如e2=e,则称e为幂等元,用I×(L)={e∈L|e2=e}表示L中所有幂等元构成的集合.对任意的e,f∈I×(L),若ef=0,则称e与f正交.设e∈I×(L).若e不能表示成2个正交的幂等元的和,则称e是本原的.

2 极小理想的存在性

以下都假设L是交换的Zerosumfree半环.用|A|表示集合A中所含元素的个数.若|L|<∞,则称L是有限的,否则就称为无限的.令

U(L)={a∈L|ab=ba=1,b∈L},

V(L)={a∈L|a+b=b+a=0,b∈L}.

由定义1.2和1.4易知下列命题成立.

命题 2.1 设I是半环L的理想.若|I|=2,则I是L的极小理想.

命题 2.2 设a∈L是乘法吸收元,则I=〈a〉是半环L的极小理想.

值得注意的是,一般情况下,命题2.2的逆命题不一定成立.例如,半环〈Z6,+,·〉中不含乘法吸收元,但由例1.3知该半环有2个极小理想.

命题 2.3 设I是L的非零理想,则I是L的极小理想当且仅当对任意的理想H,要么IH={0},要么IH=I.

与极大理想不同的是,很多半环中是没有极小理想的.例如,通过之后要证明的定理2.2和推论2.4易知半环L=〈N,+,·,0,1〉中就没有极小理想,其中,+和·分别表示整数的普通加法和乘法运算.接下来,将讨论半环中极小理想存在的条件.

定理 2.1 半环L有极小理想的充要条件是存在非零元a∈L使得对任意的r∈L,若ra≠0,则存在r′∈L使得r′ra=a.

证明 必要性 设I是半环L上的极小理想,则存在非零元a∈L使得〈a〉⊆I.从而由定义1.2知〈a〉=I.而对任意的r,a∈L,若ra≠0,则〈ra〉=〈a〉=I.因此,存在元素r′∈L使得r′ra=a.

充分性 设I=〈a〉,则对任意的r∈L都有〈ra〉⊆〈a〉.而由已知条件存在元素r′∈L使得r′ra=a可知若ra≠0,则〈a〉⊆〈ra〉.因此I=〈a〉=〈ra〉.设J是半环L的理想满足{0}J⊆I,则存在非零元b∈J使得〈b〉⊆J⊆I=〈a〉.因此存在元素r1∈L使得b=r1a≠0.又由已知条件可知存在使得a.由此可知从而〈a〉⊆〈b〉.因此〈a〉=〈b〉=I=J,即I是极小理想.

由定理2.1可知下列推论成立.

推论 2.1 设I是半环L的理想,则I是极小理想的充要条件是存在非零元a∈I使得I=〈a〉且对任意的r∈L,ra≠0蕴含〈ra〉=〈a〉=I.即非零理想是极小理想当且仅当该理想是主理想,且其中的任意非零元都是生成元.

推论 2.2 半环L中任一非零理想都包含极小理想的充要条件是半环L的任意非零理想H都满足:对任意的r∈L,存在a∈H{0},若ra≠0,则存在r′∈L使得r′ra=a.

定理 2.2 半环L有极小理想当且仅当L中有一条稳定的理想降链.

证明 必要性 设I是L的极小理想,则I所在的任一降链都是稳定的.反之,设I0⊇I1⊇I2⊇…⊇In⊇…是一条稳定的理想降链,则由定义1.3知存在正整数n0使得In0=In0+1=….从而对L的任意理想J,由{0}⊆J⊆In0可知,要么J=In0,要么J={0}.因此In0是L的极小理想.

由定理2.2有下面结论成立.

推论 2.3 半环L的任一非零理想都包含极小理想的充要条件是L的任意非零理想都在一条稳定的理想降链上.

定理 2.3 设I是半环L的任一理想,则I是极小理想当且仅当对任意的理想I1、I2,若I=I1+I2,则要么I=I1,要么I=I2.

证明 必要性显然成立.反之,若半环L的理想J满足{0}⊆J⊆I,则J+〈IJ〉=I.若J≠{0},则I=J且IJ={0}.若J={0},则I=〈IJ〉.因此,要么J={0},要么J=I,即I是极小理想.

引理 2.1[16]若U(L)=L{0},则半环L中没有非零理想.

定理 2.4 设半环L中乘法消去律成立,则L中没有极小理想.但反之不然.

证明 对任意的0≠a∈L,r∈L,如果ra=0,则r=0.因此L是整的.假设L中有极小理想.由定理2.1知,存在非零元a∈L,使得对任意的非零元r∈L都有ra≠0.进而存在r′∈L使得r′ra=a,从而r′r=1.因此L是除半环,由引理2.1可知半环L没有非零理想,矛盾.因此L没有极小理想.反之不然,如半环〈[0,1],+,·,0,1〉中没有极小理想且消去律也不成立,其中,对任意的a,b∈[0,1],a+b=max{a,b},a·b=min{a,b}.

推论 2.4 半环〈N,+,·,0,1〉中没有极小理想,其中,+和·分别表示整数的普通加法和乘法运算.

定理 2.5 设L是满足消去律的Austere半环,则L中没有极小理想.

证明 对任意的a,b∈L,令I={r∈L|ra=rb},则对任意的r1,r2∈I,r∈L有

r1a=r1b,r2a=r2b,

(r1+r2)a=(r1+r2)b,

r1+r2∈I且rr1a=rr1b,即rr1∈I.若I≠L,则I是L的理想.假设r1∈I且r1+r2∈I,则r1a=r1b且r1a+r2a=r1b+r2b,从而r2a=r2b,r2∈I.于是I是半负的,而这与半环L是Austere的矛盾.因此I=L且1∈I,即a=b,亦即L是乘法可消的.由定理2.4知,L中没有极小理想.

定理 2.6 设L是有限阶半环,则L有极小理想当且仅当L有非零理想.

证明 必要性显然,下证充分性.设I是L的非零理想.若I不是极小理想,则存在理想J1使得{0}J1I.若J1不是极小理想,则存在理想J2使得{0}J2J1.重复以上步骤,由L是有限阶的知,必存在正整数k使得Jk是L的极小理想.

3 极小理想的性质

极小理想作为一类特殊的理想,有着一些其它理想所不具有的特殊性质,下面将讨论极小理想的一些性质.

引理 3.1[16]设I和H都是半环L的理想,则IH⊆I∩H.

引理 3.2 设I是半环L的极小理想,H是L的任一理想,则要么I∩H=I,要么I∩H={0}.

定理 3.1 设I1、I2是半环L的2个极小理想,则有:

1) 要么I1I2={0},要么有I1I2=I1=I2;

2) 对L的任意理想H都有I1H=I1∩H;

3)I1+I2也是极小理想当且仅当I1=I2;

4) 如果I1和I2中至少有负理想,那么I1∪I2是半环L的理想当且仅当I1=I2.

证明 1) 若I1I2≠0,则存在非零元a∈L使得0≠a∈I1I2⊆I1.因此〈a〉=I1I2=I1.同理,知〈a〉=I1I2=I2.

2) 由引理3.2可知,要么I1∩H=I1,要么I1∩H={0}.若I1∩H={0},则显然有I1H=I1∩H.而若I1∩H=I1,则I1⊆I1H=I1∩H=I1.因此I1H=I1∩H.

3) 若I1+I2是极小理想,则由I1⊆I1+I2和I2⊆I1+I2可知I1=I2=I1+I2.反之,由推论2.1不妨设I1=I2=〈a〉,则有

〈a〉+〈a〉={r1a+r2a|r1,r2∈L}=

{ra|r∈L}=〈a〉.

因此I1+I2是极小理想.

4) 充分性显然.反之,设I1≠I2,I1=〈a〉且I2=〈b〉,其中,a,b∈L,则a∉I2,b∉I1且I1∩I2={0}.从而由I1∪I2是半环L的理想可知a+b∈I1∪I2.由已知不妨设I1是负理想,则b∈I1,矛盾.因此I1=I2.

由定理3.1可知下面2个推论成立.

推论 3.1 极小理想要么是乘法幂等的,要么是幂零的.若是幂零的,则幂零指数为2且该极小理想中任意非零元的幂零指数都为2.

推论 3.2 不同极小理想的生成元正交.

定理 3.2 设I是半环L的极小理想,则有:

(i) 对任意的t∈L,要么tI={0},要么tI=I;

(ii)I2=I当且仅当存在0≠a,b∈I使得ab≠0;

(iii)I2={0}的充要条件是存在0≠a,b∈I使得ab=0;

(iv)I是半环的充要条件是I中存在乘法幂等元.进一步地,若I是半环,则I是乘法正则的除半环;

(v) 若I2≠{0},则I中有乘法幂等元.

证明 (i) 若tI≠{0},则tI⊆I且tI是理想.因此tI=I.

由定理2.1知,(ii)和(iii)显然成立.

(iv) 充分性 设e是I中的乘法幂等元.由推论2.1,不妨设I=〈e〉,则显然(I,+)是幺半群,(I,·)是半群,且对任意的re∈I,由ree=re可知e是I中的单位元.因此〈I,+,·,0,e〉是半环.进一步地,对任意的r∈L,若re≠0,则存在r′∈L使得r′re=e且r′ere=r′ree=r′re=e.因此r′e是re的乘法逆元,即I是除半环.又对任意的0≠re∈I,其中,r∈L,存在r′∈L使得re=ere=r′rere=re(r′e)re,因此I是乘法正则的.反之显然成立,因为e2=e,其中,e是I的单位元.

(v) 首先证明对任意的0≠a∈I,有Ia=I.若存在非零元a0∈I,使得Ia0={0}.令J={a∈I|Ia={0}}且I=〈c〉,其中c∈L.于是有IJ={0}且对任意的a1,a2∈J有

I(a1+a2)={rc(a1+a2)|r∈L}=

{rca1+rca2|r∈L}={0},

因此a1+a2∈J.又对任意的r∈L,由Ira1={0}可知J是L的非零理想且J⊆I,从而I=J且IJ=I2={0},矛盾.因此对任意的0≠a∈I都有Ia=I.这意味着对任意的a,b∈I,方程ax=b在I中都有解.对任意的a,c∈L,令ae=a且c=ar,其中,e,r∈L,则由L是交换半环可知ce=are=rae=ra=c,这意味着e是I的单位元.因此〈I,+,·,0,e〉是半环且e2=e.

由定理3.2的(ii)和(iii)可知,如果在极小理想I中有零因子,则I的任意非零元都是零因子.相应地,如果I中存在元素不是零因子,则I中不含零因子.1958年,S. Bourne在文献[15]中,应用Euler的论证方法证明了当I是L的有限阶极小右理想时,要么I2={0},要么I含有乘法幂等元.1993年,陈培慈[17]在L是有效半环且L的每个非零理想都包含极小左理想与极小右理想的条件下证明了L的每个非零理想包含乘法幂等元.

定理 3.3 设I=〈e〉是半环L的极小理想.若I是半环,则e不能表示成2个正交的乘法幂等元的和.若I2=I且e不是本原的,则I不是极小理想.

证明 若e不是本原的,即存在元素a,b∈I×(L)使得ab=0且e=a+b,则有

ea=a2+ab=a∈I,

eb=b2+ab=b∈I.

因此由定理3.2(iv)可知a和b都是I的乘法单位元,从而由单位元的唯一性知a=b=e,而这与ab=a=b≠0矛盾.因此e是本原的.进而由定义1.7知道I能分解成2个主理想的直和.因此I不是极小理想.

推论 3.3 若半环L中存在极小理想不是幂零的,则L中必存在本原的乘法幂等元.

定理 3.4 设I=〈e〉是半环L的极小理想.若e是乘法幂等元,则I要么是Zerosumfree半环,要么是域.

证明 若I不是Zerosumfree半环,则V(I)≠{0}.对任意的a,b∈V(I),存在a1,b1∈I使得a+a1=0,b+b1=0,故a+b∈V(I).又对任意的r∈L,由ra+ra1=0可知ra∈V(I)且V(I)⊆I,从而1∉V(I).因此V(I)是L的理想且V(I)=I,即I是域.

定理 3.5 设I和H分别是半环L的极小理想和极大理想,则要么I+H=H,要么I+H=L.

引理 3.3[16]半环的任意理想都包含于它的极大理想.

定理 3.6 极小理想I在半环L中是可补的当且仅当存在L的一极大理想H,使得I∩H={0}.

证明 若存在理想K满足I+K=L且I∩K={0},则存在r1∈I,r2∈K使得r1+r2=1.设H是包含K的极大理想,则I+H=L.若I∩H≠{0},则I⊆H且r1,r2∈H,这意味着1∈H,即H=L,矛盾.因此I∩H={0}.反之,H即是I的补理想.

4 有极小理想的半环的结构

下面将讨论有极小理想的半环的性质并给出相应半环的Wedderburn结构.

定理 4.1 设半环L有极小理想I,则L是整的当且仅当I是L的唯一极小理想且I中无零因子.

证明 必要性 设半环L是整的,J是它的极小理想,则JI≠{0}且I=IJ⊆I∩J.因此I=J.反之,由定理3.2易知I2=I.若存在0≠a,b∈L使得ab=0,则由极小理想的唯一性知I⊆〈a〉,I⊆〈b〉且I2⊆〈a〉〈b〉={0},矛盾.因此L是整的.

定义 4.1[17]L是Artin半环当且仅当ideal(L)的任意子集都包含极小元.若Artin半环不含非零的幂零理想,则称该Artin半环为半单的.

引理 4.1[12]L是Artin半环当且仅当L中的任意理想降链都是稳定的.

由引理4.1和定义4.1易见L是Artin半环当且仅当L的任意非零理想都包含极小理想.

推论 4.1 任意有极小理想的整半环都是Artin半环.

由定理3.2(iv)的证明知下面定理显然成立.

定理 4.2 设L是有极小理想的乘法幂等半环,则L的任一极小理想都只包含非零元.

由定理4.1和4.2可知下面推论成立.

推论 4.2 设L是Artin半环,则下面3个条件等价:

1) 半环L中不含非零幂零理想;

2) 半环L的任意极小理想都是幂等的;

3) 半环L是半单的.

定义 4.2[16]设L和S是2个半环.若映射γ:L→S满足下列条件:

1)γ(0L)=0S,γ(1L)=1S;

2)γ(r+r′)=γ(r)+γ(r′);

3) 对任意的r,r′∈L,γ(rr′)=γ(r)γ(r′),

则称γ是半环L到S的同态映射.特别的,若同态映射γ是单射,则称之为单同态,若同态映射γ是满射,则称为满同态.既是单同态又是满同态,则称之为同构映射.

定理 4.3 设I是半环L上的极小理想.若I是幂等的,则存在L到I的满同态.

证明 不妨设I=〈e〉,对任意的r∈L,令γ:L→I,r|→re,则容易看出γ是满射且γ(0R)=0I,γ(1R)=1I.又对任意的r∈L有

γ(r+r′)=(r+r′)e=

re+r′e=γ(r)+γ(r′),

γ(rr′)=rr′e=rer′e=γ(r)γ(r′).

因此γ(r)是L到I的满同态.

定理 4.4 设L是有极小理想的半环,且

则M2(L)既有极小左理想也有极小右理想.

证明 设I=〈e〉是半环L的极小理想,令

则对任意的A∈M2(L),

AI1∈Δ,从而Δ是M2(L)的理想.现设J是M2(L)的一左理想且{0}≠J⊆Δ,则存在非零矩阵

J.

设

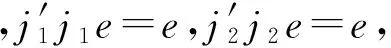
J.

因此Δ是M2(L)的一极小左理想.对极小右理想的情况同理可证.

定理 4.5 设γ:L→S是半环L到半环S的满同态,I=〈a〉是L的极小理想,则γ(I)是S的极小理想当且仅当γ(a)≠0S.且若I是幂等的,则γ(I)也是幂等的.

证明 必要性显然成立,因此只需证明充分性即可.设γ(a)=b≠0S,则对任意的0S≠s∈S,存在0L≠r∈L使得γ(r)=s.由定理2.1知要么r′ra=a,r′∈L,要么ra=0L.如果r′ra=a,r′∈L有

γ(a)=γ(r′ra)=γ(r′)γ(r)γ(a).

从而对任意的s∈S,都存在s′=γ(r′)使得s′sb=b.因此由定理2.1可知γ(I)=γ(〈a〉)=〈b〉是S的极小理想.如果ra=0L,有s′b=0S.因此γ(I)是S的极小理想.进一步地,若I是幂等的,则γ(I)也是幂等的.

引理 4.2[16]设γ:L→S是半环L到半环S的满同态,H是L的极小理想,则γ(H)也是S的理想.

定理 4.6 设γ:L→S是半环L到半环S的满同态,H=〈b〉是S的极小理想,其中,γ(a)=b,a∈L,b∈S,则γ(〈a〉)=H=〈γ(a)〉,且对任意的理想J,若0≠J⊆γ-1(H),则γ(J)=H.

证明 首先证明

γ-1(H)={r∈L|γ(r)∈H}

是L的理想.对任意的r1,r2∈γ-1(H),由

γ-1(r1+r2)=γ-1(r1)+γ-1(r2)∈H

可知r1+r2∈γ-1(H).又若r∈L,c∈γ-1(H),则

γ(rc)=γ(r)γ(c)∈H,

从而rc∈γ-1(H).因此γ-1(H)是L的理想.进一步,因为γ是满射,知道存在a∈L使得γ(a)=b,从而a∈γ-1(H)且a≠0L.因此〈a〉⊆γ-1(H)且γ(〈a〉)⊆γγ-1(H)⊆H.又由引理4.2知道γ(〈a〉)是S的理想,因此γ(〈a〉)=H=〈γ(a)〉.

设J是L的理想使得{0}≠J⊆γ-1(H),则存在非零元c∈J使得c∈γ-1(H).也就是说γ(c)∈H且〈c〉⊆γ-1(H).因此

γ(〈c〉)⊆γ(J)⊆γγ-1(H)⊆H,

于是γ(〈c〉)=H=γ(J).

定义 4.3[16]设I是半环L的理想.对任意的r∈L,令

r/I={r′|r+a=r′+b,a,b∈I},

L/I={r/I|r∈L}.

在L/I上定义算子+和·如下:对任意的r,r′∈L,r/I+r′/I=r+r′/I,r/I·r′/I=r·r′/I,则L/I=〈L/I,+,·,0/I,1/I〉是半环,称为L的商半环.

定理 4.7 设L是Artin半环,则对L的任意理想I,L/I也是Artin半环.

证明 定义映射f:L→L/I满足：对任意的r∈L,f(r)=r/I,易见f是满射.设H1⊇H2⊇…⊇Hn⊇…是L/I上的任一理想降链,则f-1(H1)⊇f-1(H2)⊇…⊇f-1(Hn)⊇….又L是Artin半环,故存在n0使得f-1(Hn0)=f-1(Hn0+1)=…,因此ff-1(Hn0)=ff-1(Hn0+1)=…,即H1⊇H2⊇…⊇Hn⊇…也是稳定的.因此L/I是Artin半环.

引理 4.3 设I和J是半环L的2个理想.若0⊆I⊆J,则J=I+〈JI〉.

由引理4.3知下面引理成立.

引理 4.4 商半环L/I的任意理想都可表示成形如(I+H)/I的形式,其中H是L的理想.

定理 4.8 设(ideal(L),+,∩)是模格.若L/A是Artin半环,其中,A是L的非零理想且A的任意非零理想都包含极小理想,则L是Artin半环.

证明 任取L中的一理想降链I1⊇I2⊇…⊇In⊇….若L/A是Artin半环,则存在m使得

Im+A=Im+i+A,i=1,2,….

因此Ip∩A,p=1,2,…,是A的理想,从而存在n≥m使得

In∩A=In+i∩A,i=1,2,….

若Ip⊇Iq,则Ip∩(Iq+A)=Iq+(Ip∩A),从而

In=In∩(In+A)=

In∩(In+i+A)=In+i+(In∩A)=

In+i+(In+i∩A)=In+i.

因此L是Artin半环.

引理 4.5 2个幂零理想的和仍是幂零的.

}.

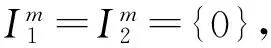
因此I1+I2是幂零的.

引理 4.6 设L是半环且I×(L)≠{0},则L中存在唯一最大幂零理想N,它包含L中所有幂零理想且L/N中没有非零的幂零理想.

证明 设N是L中所有幂零理想的和,则由引理4.5知N是幂零的,且由I×(L)≠{0}知N≠L.若B/N是L/N的非零的幂零理想,则NB.如果(B/N)m=Bm/N=0/N且Nn={0},则(Bm)n⊆Nn={0}.因此B是幂零的,矛盾.

定理 4.9 设L是Artin半环,则L的任一非幂零理想都包含乘法幂等元.

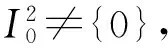
定理 4.10 (Artin半环的Wedderburn结构)半环L是半单的当且仅当它是有限个幂等的极小理想的直和.

证明 充分性 设L=I1⊕I2⊕…⊕In,其中,I1,I2,…,In都是L的极小理想,则L的任意理想H都是某些Ii的直和且都包含一极小理想,从而ideal(L)是模.因此H2=H且L中没有幂零理想.下证L是Artin半环.n=2时结论显然成立,假设n=k时结论成立.设L=I1⊕I2⊕…⊕Ik+1且A=I1⊕I2⊕…⊕Ik,则由归纳假设知A是Artin的,因此L/A也是Artin的.从而由定理4.8知L是Artin的,因此L是半单的.反之,若L是半单的且有极小理想I1,则

L=I1+〈L/I1〉.

若〈L/I1〉是L的极小理想,则由定理3.1的2)知I1∩〈L/I1〉={0},也就意味着I1⊕〈L/I1〉=L.否则存在极小理想I2使得

〈L/I1〉=I2+〈〈L/I1〉/I2〉.

若〈〈L/I1〉/I2〉是极小理想,则

〈L/I1〉=I2⊕〈〈L/I1〉/I2〉,

且要么

L=I2⊕〈〈L/I1〉/I2〉,

要么

L=I1⊕I2⊕〈〈L/I1〉/I2〉.

若〈L/I1〉/I2〉不是极小理想,则按以上方法如此下去,能得到理想降链

〈L/I1〉⊇〈〈L/I1〉/I2〉⊇〈〈〈L/I1〉/I2〉/I3〉…,

由L是Artin的必有L是有限个极小理想的直和.

值得注意的是,定理4.9与文献[15,18]中的结论是不同的,我们给出了半环是半单的充要条件,这与Artin环的Wedderburn结构相似.

推论 4.3 若L是半单半环,则它的单位元1能分解成有限个正交乘法幂等元的和.

5 结论

本文主要讨论了有极小理想的半环的结构.首先给出了极小理想存在的一些充要条件,然后借助极小理想给出了半环的Wedderburn结构.值得指出的是,上面所有的结果都建立在交换半环上,然而同样的结论在非交换半环上是否成立仍然是公开问题.

[1] Vandiver H S. Note on a simple type of algebra in which cancellation law of addition does not hold[J]. Bull Am Math Soc,1934,40:914-920.

[2] Aho A V, Ullman J D. Languages and Computation[M]. Reading MA:Addison Wesley,1976.

[3] Feng F, Jun Y B, Zhao X Z. On *-μ-semirings[J]. Inform Sci,2007,177:5012-5023.

[4] Glazek K. A Guide to Literature on Semirings and Their Applications in Mathematics and Information Science:with Complete Billiography[M]. Dordrecht:Kluwer Acad Publ,2002.

[5] Hebisch U, Weinert H J. Semirings:Algebraic Theory and Applications in the Computer Science[M]. Singapore:World Scientific,1998.

[6] Kuich W. Automata and languages generalized toω-continuous semirings[J]. Theory Comput Sci,1991,79:137-150.

[7] Roman S. Coding Theory and Information Theory[C]//Graduate Texts in Mathematics. New York:Springer-Verlag,1992.

[8] Shry H J. Free Monoids and Languages[D]. Taipei:Soochow University,1979.

[9] LaGrassa S. Semirings:Ideals and Polynomials[D]. Iowa:University of Iowa,1995.

[10] Alarcon F E, Anderson D D. Commutative semirings and their lattices of ideals[J]. Houston J Math,1994,20:571-590.

[11] Henriksen M. Ideal in semirings with commutative addition[J]. Noties Am Math Soc,1958,5:321.

[12] Iizuka K. On the Jacobson radical of a semiring[J]. Tohoku Math J,1959,11(2):409-421.

[13] La Torre D R. Onh-ideals andk-ideals in hemirings[J]. Publ Math Debrecen,1965,12:219-226.

[14] Ma X, Zhan J. Generalized fuzzyh-ideals andh-quasi-ideals of hemirings[J]. Inform Sci,2009,179:1249-1268.

[15] Bourne S. On multiplicative idempotents of a potent semiring[J]. Proc Nat Acad Sci USA,1956,42:632-638.

[16] Golan J S. Semirings and Their Applications[M]. Dordrecht:Kluwer Acad Publ,1999.

[17] 陈培慈. 半环理论与语言和自动机[M]. 南昌:江西高校出版社,1993.

[18] Bourne S, Zassenhaus H. On a Wedderburn-Artin structure theory of a potent semiring[J]. Proc Nat Acad Sci USA,1957,43:613-615.

[19] 王绘莉,王学平. 两类特殊S0-模糊传递矩阵的收敛性[J]. 四川师范大学学报:自然科学版,2012,35(2):151-156.

[20] 王绘莉,舒乾宇,王学平. Max-plus代数中analogy-transitive矩阵及其本征问题[J]. 四川师范大学学报:自然科学版,2014,37(3):293-297.

[21] 熊清泉,舒乾宇. 完备格上区间值t-半模及其R-蕴含算子[J]. 四川师范大学学报:自然科学版,2013,36(2):165-170.

2010 MSC：16Y60

(编辑 李德华)

Semirings with Minimal Ideals

HE Peng, SHU Qianyu
(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

This paper investigates the existence of minimal ideal in semirings and the structure of semiring with minimal ideal. Some sufficient and necessary conditions for the existence of minimal ideals in a semiring are given, some characterizations of minimal ideals are studied and the structure of semirings with minimal ideals is described.

semiring; minimal ideal; Wedderburn structure

2014-06-23

国家自然科学基金(11401410)、教育部博士点基金(20105134110002)和四川省教育厅自然科学青年基金(13ZB0165)

O153.3

A

1001-8395(2015)06-0810-08

10.3969/j.issn.1001-8395.2015.06.004

*通信作者简介：舒乾宇(1982—),女,副教授,主要从事半环的研究,E-mail:34956229@qq.com