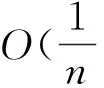|x|α在第二类Chebyshev结点的有理插值
2015-05-04张慧明段生贵李建俊石家庄经济学院数理学院河北石家庄05003河北师范大学附属民族学院河北石家庄05009
张慧明, 段生贵, 李建俊(. 石家庄经济学院 数理学院, 河北 石家庄 05003; . 河北师范大学 附属民族学院, 河北 石家庄 05009)
|x|α在第二类Chebyshev结点的有理插值
张慧明1, 段生贵1, 李建俊2
(1. 石家庄经济学院 数理学院, 河北 石家庄 050031; 2. 河北师范大学 附属民族学院, 河北 石家庄 050091)
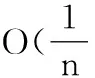
Lagrange插值; 第二类Chebyshev结点; 有理插值; Newman-α型有理算子; 逼近阶
1 引言及预备知识
令f(x)∈C[-1,1],则基于结点组X={xk:-1≤x0 其中 f的连续性并不能保证在n→∞时,Ln(f,X,x)处处收敛于f(x). 1918年,S. Bernstein[1]证明了一个经典的结果,即对于等距结点 j=0,1,2,…,n,n∈N, ∀x∈(-1,1), |x|的Lagrange插值多项式逼近|x|也是除了±1和0外处处发散.1964年,D. J. Newman[16]引入有理函数rn(x),发现它远远优于其Lagrange插值多项式逼近,得到结果:当n≥5时,有下式成立 由于有理函数对于|x|有很好的逼近效果,是否也可以考虑用有理函数逼近|x|α(0<α<1)? 本文类似于Newman型有理算子[17]定义如下Newman-α型有理算子 其中 结点组可以取作 X={xk:0 当α=1时,也就是以前考虑|x|的有理插值问题,相应的Newman-α型有理算子也就是Newman型有理算子. 文献[17]构造的Newman型有理算子在(-∞,+∞)与|x|有共单调性,现在构造的Newman-α型有理算子在(-∞,+∞)有同样的性质. 定理 1rn,α(X;x)在(-∞,+∞)与|x|α有共单调性. Y={0 其中 结点组取作Y={0 由于rn,α(X;x)和|x|α都是偶函数,可得:rn,α(X;x)在(-∞,+∞)与|x|α有共单调性.所以只需考虑[0,+∞)即可. ). 要证明以上定理需要用如下一些基本引理. 引理 1 当m1≤m2≤n时,有以下不等式成立 证明 原不等式较繁,两边同时乘以 并化简得 要证明原不等式,只需证明以上不等式,即证 引理1不等式得证. 引理 2 当a>b>1时,有以下不等式成立 证明 首先看以下不等式 (c+d)(cm-1+cm-2d+cm-3d2+…+dm-1)= cm+2(cm-1d+cm-2d2+…+cdm-1)+dm> cm+(2m-1)dm,c>d,m∈N*. 由以上两式相除即得引理2. 定理2的证明 由于rn-1,α(U;x)和|x|α均为偶函数,所以只考虑区间[0,1]即可. |en-1,α(U;x)|=||x|α-rn-1,α(U;x)|≤ 其中 由上式得 |en-1,α(U;x)|= 利用引理1中不等式得 利用引理2中不等式得 所以有 |en-1,α(U;x)|= 综合1)和2),定理得证. [1] Bernstein S. Quelques remarques surl interpolation[J]. Math Ann,1918,79:1-12. [2] Natanson I P. Constructive Function TheoryⅢ[M]. New York:Fredrick Ungar,1965:30-35. [3] Revers M. The divergence of Lagrange interpolation for |x|αat equidistant notes[J]. J Approx Theory,2000,103:269-280. [4] Revers M. On Lagrange interpolatory parabolas to |x|αat equally spaced nodes[J]. Archiv Der Math,2000,74:385-391. [5] Brutman L, Passow E. On the divergence of Lagrange interpolation to |x|[J]. J Approx Theory,1995,81:127-135. [6] 何国龙,陈志祥,周颂平. 插值多项式对函数|x|α的逼近[J]. 浙江大学学报:理学版,2004,31(1):21-23. [7] 卢志康,吴晓红. 插值多项式对函数|x|α的逼近[J]. 浙江大学学报:理学版,2006,33(6):610-612. [8] Zhu L Y, Huang Z Y. On Lagrange interpolation for |x|α(0<α<1)[J]. Analysis Theory Appl,2009,25(1):16-24. [9] 吴晓红,卢志康. 拉格朗日插值多项式对函数|x|α的逼近[J]. 杭州师范大学学报:自然科学版,2012,11(4):302-304. [10] Xia M. On Lagrange interpolation to |x|α(1<α<2) with equally spaced nodes[J]. Analysis Theory Appl,2004,20(3):281-287. [11] Lu Z K, Ge X F. The exact convergence rate at zero of Lagrange interpolation polynomial to |x|α[J]. Analysis Theory Appl,2006,23(3):201-207. [12] Revers M. On Lagrange interpolation with equally spaced nodes[J]. Bull Austral Math Soc,2000,62:357-368. [13] Su H, Xu S S. The divergence of Lagrange interpolation for |x|α(2<α<4) at equidistant nodes[J]. Analysis Theory Appl,2006,22(2):146-154. [14] 郭妞萍,黄志强. 在等距节点处对函数|x|α进行拉格朗日插值时的收敛性[J]. 西南民族大学学报:自然科学版,2006,32(6):1106-1110. [15] 黄志强,郭妞萍. 在等距节点处对函数|x|α(3<α<4)进行拉格朗日插值的收敛阶[J]. 西南民族大学学报:自然科学版,2011,37(1):19-22. [16] Newman D J. Rational approximation to |x|[J]. Mich Math J,1964,11:11-14. [17] Brutman L, Passow E. On rational interpolation to |x|[J]. Constr Approx,1997,13:381-391. [18] 张慧明,李建俊. |x|在第二类Chebyshev结点的有理逼近[J]. 郑州大学学报:理学版,2010,42(2):1-3. 2010 MSC:41A20; 41A25 (编辑 李德华) On Rational Interpolation to |x|αat the Chebyshev Nodes of the Second Kind ZHANG Huiming1, DUAN Shenggui1, LI Jianjun2 Lagrange interpolation; Chebyshev nodes of the second kind; rational interpolation; Newman-αtype rational operator; order of approximation 2014-03-14 河北省高等学校科学技术研究青年基金(QN2014018) 张慧明(1978—),男,讲师,主要从事函数逼近论的研究,E-mail:zhanghm1978@126.com O174.41 A 1001-8395(2015)06-0889-04 10.3969/j.issn.1001-8395.2015.06.019
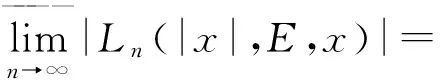

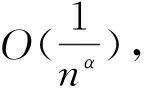

2 rn,α(X;x)在(-∞,+∞)与|x|α共单调


3 rn,α(X;x)在第二类Chebyshev结点对|x|α的有理逼近
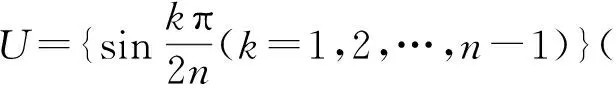



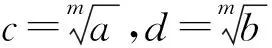
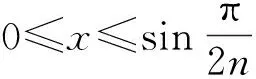


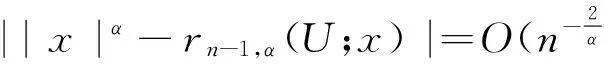
4 分析小结

(1.SchoolofMathematicsandPhysics,ShijiazhuangCollegeofEconomics,Shijiazhuang050031,Hebei;2.AffiliatedCollegeofMinorityEducation,HebeiNormalUniversity,Shijiazhuang050091,Hebei)