应用阿兹海默症基因表达数据对比2种层次聚类方法

付如意, 黄 静， 胡本琼， 庞朝阳(. 四川师范大学 数学与软件科学学院, 四川 成都 60066; . 成都理工大学 管理科学学院, 四川 成都 60059;3. 四川师范大学 计算机科学学院, 四川 成都 60066; 4. 四川师范大学 可视化计算与虚拟现实省重点实验室, 四川 成都 60066)



应用阿兹海默症基因表达数据对比2种层次聚类方法

付如意1, 黄 静1， 胡本琼2， 庞朝阳3,4*
(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 成都理工大学 管理科学学院, 四川 成都 610059;3. 四川师范大学 计算机科学学院, 四川 成都 610066; 4. 四川师范大学 可视化计算与虚拟现实省重点实验室, 四川 成都 610066)

随着基因芯片技术的发展，双聚类分析方法首先被应用到高维基因表达数据的研究中.由于多数高维数据的稀疏性，应用主成分分析方法将高维数据转化到低维数据空间，从而在低维空间中应用聚类分析方法.不同的聚类分析方法会得到不同的聚类效果，并且同一种聚类方法处理不同的高维数据也会得到不同的聚类效果.因此，首先评估了阿尔茨海默基因表达数据的特征集的聚类趋势，接下来给出了改进地δ阈值层次聚类算法的算法描述.由于已有工作分别给出了不同的δ阈值的计算规则，于是比较了它们δ阈值下的层次聚类算法，并且给出了相应的聚类评价.

层次聚类； 阈值； 基因表达数据

阿兹海默症是一类神经退行性疾病，已成为继心血管疾病、恶性肿瘤、脑卒中之后老年人的第4大“健康杀手”[1].目前，世界上并没有治疗老年痴呆症的有效办法.随着基因芯片技术[2]的迅速发展，2003年起科学家将聚类分析方法[3-5]应用到阿兹海默症相关的基因表达数据上.2009年W. Kong等[6]将独立主成分分析(ICA)方法应用于阿兹海默症的候选基因的识别中.2010年C. Y. Pang等[7]将聚类分析方法应用到阿兹海默症的致病基因的识别中.2012年C. Y. Pang等[8]应用层次聚类分析方法挖掘与阿兹海默症相关的基因表达数据.文献[9]也给出了一种简捷地无监督一维聚类方法并且应用阿兹海默症的数据对其作了数据建模.但是上述文献均没有从统计学上去评估数据的聚类趋势以及比较应用不同的聚类方法后的实验结果.因此，本文将对其阿兹海默症的基因表达数据做聚类趋势的评估.传统的层次聚类算法需要事先主观地确定出分类个数，从而接下来本文结合文献[8-9]给出了改进地δ阈值层次聚类算法的算法描述.由于文献[8]和[9]分别给出了不同的δ阈值的计算规则，于是本文通过轮廓系数指标比较分析了它们的实验结果.最后，从客观数据的角度对改进地δ阈值层次聚类算法做出评价.

1 预备知识

1.1 主成分分析方法[8]主成分分析(PCA)是一种对数据进行简化的技术.这种方法实质上是找出数据中最“主要”的元素和结构，去除噪音和冗余，将原有数据降维，揭示隐藏在复杂数据背后的简单结构.接下来将给出主成分分析方法的算法描述：

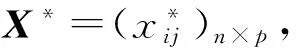
步骤二：计算相关系数矩阵R=(rxy)p×p,

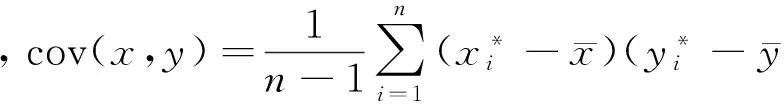
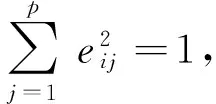
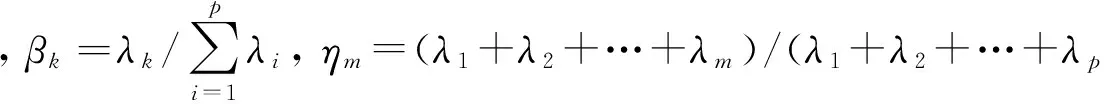
步骤五：计算主成分的载荷矩阵L=(lij)p×p和得分矩阵F.原始数据前的加权系数决定了新的综合变量主成分的大小和性质，通常称为主成分轴或者载荷向量：

原始变量在新的坐标系下投影求得在新坐标系下的变量值即为得分：

Fi=e1iX1+e2iX2+…+epiXp,i=1,2,3,…,p.

1.2 霍普金斯统计量[12]霍普金斯统计量是一种空间统计量,检验空间分布的变量的空间随机性,即确定数据空间中的数据点在多大程度上不同于均匀分布.给定数据集D，按以下步骤计算霍普金斯统计量：

1) 均匀地从D的空间中抽取n个点p1,p2,…,pn.找出pi(1≤i≤n)在D中的最近邻，并令xi为pi与它在D中的最近邻之间的距离，即

2) 均匀地从D中抽取n个点q1,q2,…,qn.找出qi(1≤i≤n)在D-{qi}中的最近邻，并令yi为qi与它在D-{qi}中的最近邻之间的距离，即

3) 计算霍普金斯统计量H,

1.3 轮廓系数[12]对于n个对象的数据集D，假设D被划分成k个簇C1,C2,…,Ck.对于每个对象o∈D,计算o与o所属的簇的其他对象之间的平均距离a(o).类似地，b(o)是o到不属于o的所有簇的最小平均距离.假设o∈Ci(1≤i≤k),则

并且

对象o的轮廓系数定义为

轮廓系数方法结合了凝聚度和分离度，可以以此来判断聚类的优良性，其值在-1到+1之间取值，值越大表示聚类效果越好.

2 数据的来源与特征

本文使用的基因表达数据是从美国国家生物技术信息中心(NCBI)网站上下载得到的[13-14].该数据为31组65～101岁年龄阶段的患有不同程度的阿兹海默症的患者的22 283个基因的表达水平值.其9组正常人的基因表达水平值数据格式如表1所示.

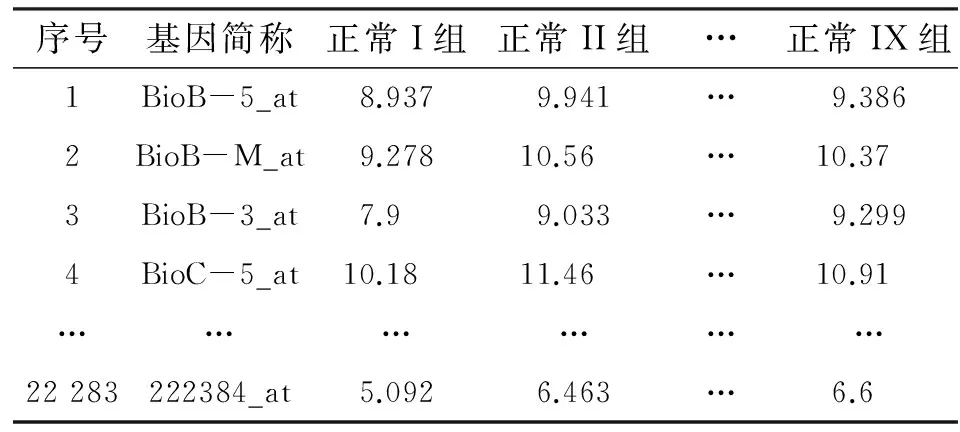
表 1 9组正常人体的22 283个基因表达水平数据表

由于31组患者的个体差异，使得如表1所示的列数据之间不可以相互比较.同时，假设同一程度的阿兹海默症患者的基因表达水平数据具有相同的特征，即表1所示的各列数据间包含了相同或相似的特征集合.文献[15]中详细地阐述了对基因组表达数据运用SVD方法进行数据建模并且处理得到了其特征集合.从而通过文献[15]所述的方法可以得到正常、轻度、中度和重度4种不同程度的基因表达水平数据的特征集合.进一步地，文献[11]详细地探讨了PCA方法的理论和应用以及其与SVD之间的关系.因此，本文通过PCA方法提取基因表达数据的特征集合,即主成分.

根据2.1节PCA方法的算法描述,于是分别对4种程度下的数据应用PCA方法得到了对应的特征空间.其特征值分布如图1所示.

并且，进一步可以分别计算出4种程度下的特征集的累计贡献率CPR，如表2所示.

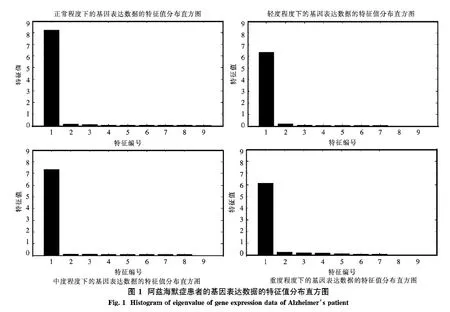
表 2 正常、轻度、中度和重度阿兹海默症患者的基因表达数据的特征集的累计贡献率表

特征集1特征集1～2特征集1～3特征集1～4特征集1～5特征集1～6特征集1～7特征集1～8特征集1～9正常0.910.930.950.960.970.980.980.991轻度0.910.940.960.970.980.991.00中度0.920.930.950.960.970.980.991.00重度0.870.910.940.960.970.991.00

从统计学意义上来说，若特征值集的累计贡献率达到了85%～95%，该特征值集为数据集的主要特征.从而由表2的数据发现，4种程度下的特征1上的累计贡献率均已达到了85%.从而由特征1上的数据来反映原始数据是可行的.

接下来则需要检验其特征1的数据是否具有聚类趋势以应用其层次聚类方法.本文采用霍普金斯统计量来估计其聚类趋势，使用0.5作为拒绝备择假设阈值，即如果H>0.5，则D不大可能具有统计显著的簇.根据2.2节的霍普金斯统计量的计算描述运用R语言编制出程序分别计算出它们在特征1上的霍普金斯统计量:正常组、轻度组、中度组、重度组的H值分别为0.051 1、0.037 8、0.068 4、0.097 1.可以发现H均远远小于0.5，即接受备择假设，也意味着4种程度下的特征1上的数据均具有统计显著的簇.从而说明特征1上的数据具有聚类效果.于是聚类分析方法能够被应用到特征1上去挖掘出不同程度的阿兹海默症患者的22 283个基因所反映出的聚类模式.

3 δ阈值层次聚类算法

在文献[8]的基础上，对层次聚类算法的阈值做出了说明，得到了δ阈值层次聚类算法.接下来，以9组正常人的基因表达数据为例来阐述该算法，由上一节可以得到9组正常人的基因表达水平数据的特征子空间，记为C.假设人体内所有的基因在特征子空间C内数据表示为Y=(yij)nm，其中，n=22 283且m为特征子空间C的维数.并且设δ=(δ1,δ2,…,δm)，其中，δi的计算规则在文献[9]中也给出了.接下来给出δ阈值层次聚类方法的算法描述：

输入：样本点集合Y，阈值δ.

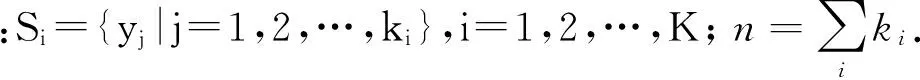
算法：

第1步，初始化K=1，S1=Y，且i=1；

第2步，令Z=Yi=(yji)n,1，并且计算出阈值δi；

第3步，若‖ysi-yti‖>δi，则s,t分别属于2类，且K=K+1，SK-1=SK-1-{yt}以及SK=SK∪{yt}，否则它们属于同一类别，即SK=SK∪{yt}；

第4步，记i=i+1，若i>m，则算法停止，否则转向第2步.

根据上述的算法描述，可以得到4种不同程度患者的基因表达数据的聚类分析结果.并且通过对文献[8]和文献[9]的聚类结果比较评估2种层次聚类算法的聚类质量.

4 实验与结果

首先，将31组阿兹海默症患者的基因表达数据划分为正常、轻度、中度和重度4种程度.其次，对于每一种程度的基因表达数据分别应用由文献[8]和文献[9]给出的δ阈值计算规则的层次聚类算法得到相应的聚类模式.最后，对2组聚类模式衡量它们的聚类质量进行比较分析，通常是按照无基准来选定方法：如果有可用的基准，外在方法可以比较聚类结果和基准，从而测定聚类质量；如果没有基准，则内在方法通过考虑簇分离情况即簇的紧凑情况来评估聚类好坏.许多内在方法都利用数据集的对象之间的相似性度量.这里，计算了衡量聚类质量的指标——轮廓系数SC，其相关的统计数据如表3所示.

最后，通过比较表3所示的数据发现，文献[8]对应列的数据均大于文献[9]中的数据.

5 结语

结合文献[8,9],本文给出了改进地δ阈值层次聚类算法的算法描述.并且对阿兹海默症基因数据应用此层次聚类算法，通过比较聚类质量指标——轮廓系数，可以发现文献[8]通过特征集中的特征值确定的阈值较优于文献[9]通过曲率最大点确定的阈值.从而进一步说明由文献[8]给出的δ阈值的层次聚类算法较客观，即本文对改进地δ阈值层次聚类算法的参数δ做出了评估.

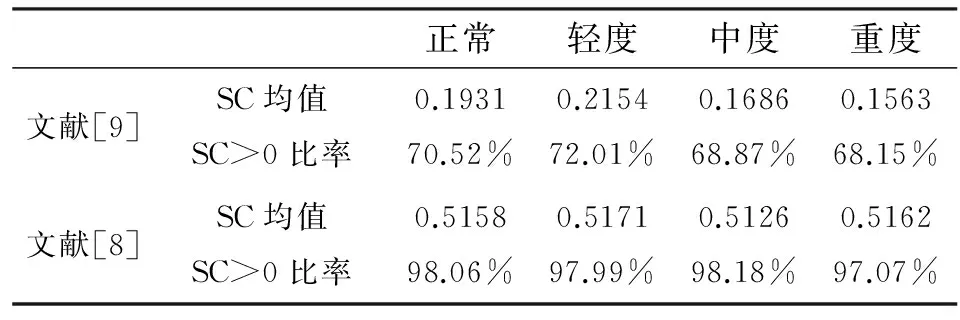
表 3 2类层次聚类算法的聚类质量指标:轮廓系数的比较

[1] 阿兹海默病. http://zh.wikipedia.org/wiki/阿兹海默病[EB/OL]. 维基百科,2014.

[2] 李瑶. 基因芯片技术:解码生命[M]. 北京:化学工业出版社,2004:77-156.

[3] 胡本琼,张先迪,庞朝阳. 利用图论设计图像压缩中的向量量化聚类算法[J]. 四川师范大学学报:自然科学版,2005,28(3):376-378.

[4] 王开军,李晓. 基于有效性指标的聚类算法选择[J]. 四川师范大学学报:自然科学版,2011,34(6):915-918.

[5] 庄刘,曾艳. 基于模糊C-均值聚类的最优量化器设计[J]. 四川师范大学学报:自然科学版.2010,33(4):559-562.

[6] Kong W, Mou X Y, Yang B. Study DNA microarray gene expression data of Alzheimer’s disease by independent component analysis[J]. Bioinformatics, Systems Biology and Intelligent Computing,2009.

[7] Pang C Y, Hu W, Hu B Q, et al. A special local clustering algorithm for identifying the genes associated with Alzheimer’s disease[J]. IEEE Trans Nanobioscience,2010.

[8] Pang C Y, Liu S Q, Li Y, et al. The nonlinear correlation character of gene expression data on Alzheimer’s disease and hierarchy clustering of co-regulated gene[J]. 2011 IEEE International Conference on Granular Computing,2011.

[9] 黄静,付如意,彭志红,等. 基于阿尔茨海默病的基因表达数据改进的一维聚类方法[J]. 四川师范大学学报:自然科学版,2015,38(4):584-588.

[10] 茆诗松,王静龙,濮晓龙. 高等数理统计[M]. 2版. 北京:高等教育出版社,2006:128-135.

[11] Jonathon S. A tutorial on principal component analysis[D]. Ithaca:Cornell University,2014.

[12] Han J W, Kamber M, Pei J. Data Mining Concepts and Techniques[M]. Beijing:China Machine Press,2012.

[13] GEO DataSet. http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE1297[EB/OL]. NCBI,2014.

[14] Blalock E M, Geddes J W, Chen K C, et al. Incipient Alzheimer’s disease:microarray correlation analyses reveal major transcriptional and tumor suppressor responses[J]. PNAS,2004,101(7):2173-2178.

[15] O Alter, P O Brown, D Botstein. Singular value decomposition for genome-wide expression data processing and modeling[J]. PNAS,2000,97(18):10101-10106.

2010 MSC：62H30; 62P10; 91C20

(编辑 周 俊)

Comparison of Two Hierarchical Clustering Methods in Gene Expression Data of Alzheimer’s Disease

FU Ruyi1, HUANG Jing1, HU Benqiong2, PANG Chaoyang3,4
(1.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan;2.CollegeofManagementScience,ChengduUniversityofTechnology,Chengdu610059,Sichuan;3.CollegeofComputerScience,SichuanNormalUniversity,Chengdu610066,Sichuan;4.VisualComputingandVirtualRealityKeyLaboratoryofSichuanProvince,SichuanNormalUniversity,Chengdu610066,Sichuan)

With the development of gene microarray technology, biclustering is applied to the research of high dimension of gene expression data. Due to the sparsity of most high-dimensional data, high-dimensional data are transferred into low-dimensional data by dimensionality reduction and so, it could be clustering in the low-dimensional data. Meanwhile, a variety of clustering appear different pattern and different data appears to different pattern for the established clustering. For gene expression data of Alzheimer’s disease, clustering tendency of feature sets is evaluated. Then, algorithm of improved hierarchical clustering with parameterδis described. References before establish computing method of parameterδ, respectively. Thus, two improved hierarchical clusterings with parameterδassigned different value are compared and clustering measure named silhouette coefficient is computed, respectively.

hierarchical clustering; threshold; gene expression data

2014-10-16

中国航空科学基金(2012ZD11)

O242.1

A

1001-8395(2015)06-0925-05

10.3969/j.issn.1001-8395.2015.06.025

*通信作者简介：庞朝阳(1973—)，男，教授，主要从事基因计算与量子力学的研究，E-mail:cypang402@126.com