板形缺陷与板材横向厚度分布的映射研究

黄长清，崔广亮

（中南大学 高性能复杂制造国家重点实验室，湖南 长沙 410083）

0 引言

由于工业部门生产发展的需要，对轧件的板形质量要求日趋严格。随着板带控制系统的发展，板带的横向厚度分布控制精度越来越高，相比之下，板形问题变得越来越突出［1］。只用板凸度的指标衡量板的精度已经不适应要求，需要同时用板凸度与板形指标进行衡量。

目前国内铝板带热轧过程都没有配置板形仪，板形的缺陷无法直接通过仪器测量。当带材在轧制中出现板形问题时，必然要引起前张力的不均匀分布。文献［2］建立了前张力分布、横向厚差与板形之间的关系。以前张力分布为桥梁，通过横向厚度分布可以预测板形好坏。轧后板材的出口断面形状被认为是有载辊缝形状，轧后板材断面形状归结为求解承载辊缝形状［3］。通过求轧辊的弹性变形可以得到有载辊缝的形状，即横向厚差分布。求解轧辊的弹性变形的方法有有限元法、影响函数法和初等解析法。有限元法分析精度高但是计算耗时多；初等解析法做了很多简化和假设，精度低而且很难求出解析解；影响函数法计算精度较高，迭代计算速度快，方便进行大量的轧制工况计算和分析［4］，如文献［5］采用显式动力学有限元法分析压下率对轧制压力横向分布的影响。但采用影响函数法系统地分析各种影响因素（如弯辊力、轧辊辊型、辊径等）及其影响规律的文献却较少。

为了能够快速计算板材横向厚度分布，本文采用影响函数法计算轧辊的有载辊缝形状，即板材出口厚度分布，并通过前张应力与板材横向厚度的关系，找出板形与板才横向厚度的映射关系。

1 板厚横向分布与板形的关系推导

设板带入口任意x处板厚为H（x），长度为L（x）；板带出口任意x处板厚为h（x），长度为l（x）。根据板形理论中的金属体积不变定律，变形区入口与出口处的金属流量相等，考虑到轧制的板材较薄（一般认为小于6mm）［6］，金属的横向流动可忽略，所以有：

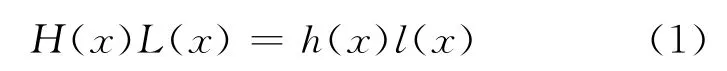
由（1）式变换得：

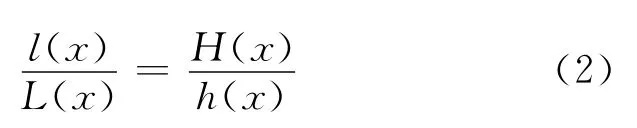
假设来料横向厚度为矩形，则H（x）与x无关，是一个常数H，则由（2）式可得：

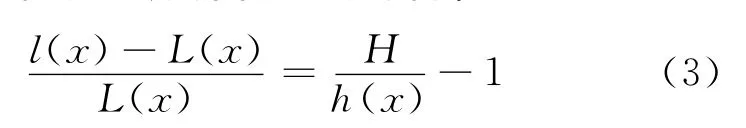
板形是板带纵向延伸长度差，表达式为：

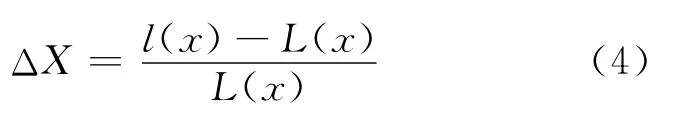
根据文献［7］的研究，板带出口前张应力分布与出口板形一一对应，其关系为：

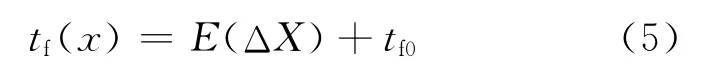
其中，tf（x）为出口x位置的前张应力；E为轧件的杨氏模量；tf0为出口板宽中心前张应力。

将（3）式代入（5）式得：

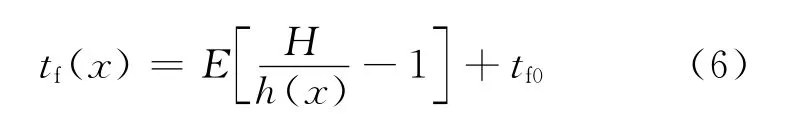
由（6）式可以看出，前张应力的分布与板带出口厚度分布有关，则板形也与板带出口横向厚度分布有关，所以可以通过分析板带出口的横向厚度分布情况，找出板形缺陷与板厚横向分布的映射关系。本文根据影响函数法求解h（x），通过（6）式的换算，找出板形缺陷与板厚横向分布的关系。

2 基于影响函数法求解出口板厚分布

2.1 影响函数法的基本原理

影响函数方法的基本思想是将连续的整体分割成若干单元，将所有的承受载荷及产生的变形进行相应的单元分割，依据数学物理方法中的影响函数的概念，确定对各单元施加单位力时在辊身各点引起的变形；然后将所有载荷引起的变形进行叠加，得出各单元的变形值；最后通过轧辊受力弹性变形、辊间接触压扁及工作辊与轧件的变形协调方程进行迭代计算，求出轧件的出口横向厚度分布。

在一般的对称轧制中，轧辊所承受的载荷及其变形是左右对称的，大多数情况下为了计算简单，都是以半辊身长为研究对象，对于非对称的轧制过程，可以考虑辊身全长，但基本方法是一样的。本文以对称轧制进行分析，取轧机的下工作辊与下支承辊为研究对象，将半辊身简化成悬臂梁，轧辊中心端固定，辊间部分为自由端，轧辊单元分割模型如图1所示。将轧件从板宽中点到边部划分为m个单元，轧辊中心到轧辊轴肩划分为n个单元，各单元的序号分别为i（i＝1，2，3，…，m）和j（j＝1，2，3，…，n）。

图1 轧辊单元分割模型

设单元长度为Δx，则轧件与轧辊各单元中点到固定端的距离分别为xi＝（i－1/2）Δx（i＝1，2，3，…，n）和xj＝（j－1/2）Δx（j＝1，2，3，…，m），按上述方法将工作辊与支承辊的作用力和变形进行离散化，并用集中载荷代表各单元的分布载荷，则有：

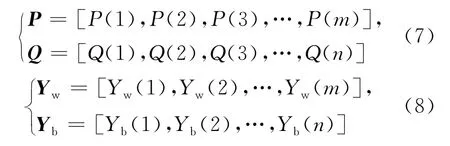
其中，P、Q分别为轧制压力向量和辊间压力向量；Yw、Yb分别为工作辊和支承辊的挠度向量。

根据影响函数的概念［8］，在j单元作用单位力p（j）时，在i单元引起的变形为y（i，j）＝g（i，j）p（j），其中，g（i，j）为j单元上p（j）对i单元变形的影响函数。

2.2 影响函数的确定

（1）工作辊弹性弯曲影响函数。其表达式如下：

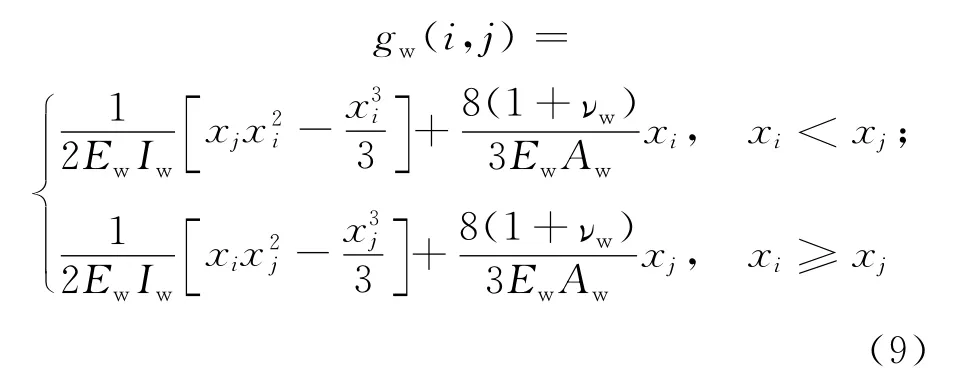
其中，Ew、Iw、Aw和νw分别为工作辊的弹性模量、惯性矩、横截面积和泊松比。

（2）支承辊弹性弯曲影响函数。其表达式为：

其中，Eb、Ib、Ab和νb分别为支承辊的弹性模量、惯性矩、横截面积和泊松比；Lp为作用在支承辊的2个轴承座之间的距离。

（3）工作辊与轧件接触的弹性压扁影响函数［8］。其表达式为：

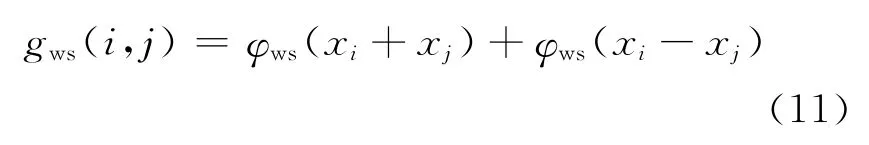
其中，

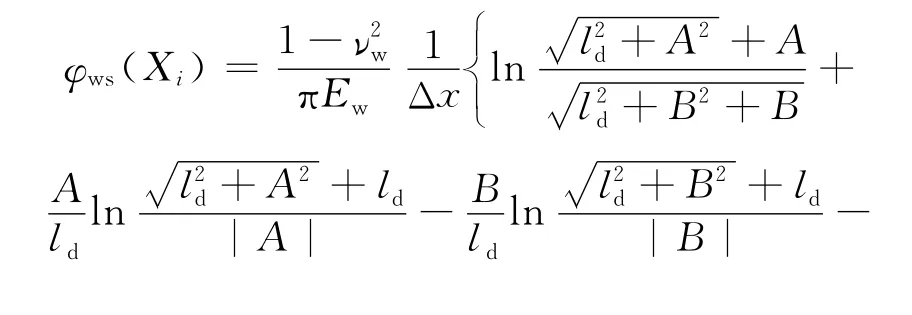
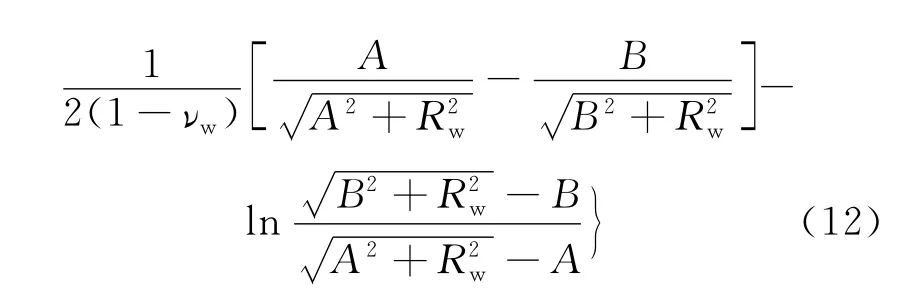
其中，A＝Xi＋Δx/2，Xi为j点到i点的距离，Xi＝xi＋xj或者Xi＝xi－xj；B＝Xi－Δx/2；ld为接触弧长度，i单元接触弧长度按Hitchcock公式确定为：

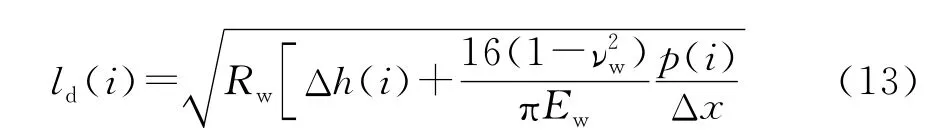
其中，Δh（i）＝H（i）－h（i）为j单元轧件的绝对压下量，H（i）和h（i）分别为单元入口和出口的厚度；Rw为工作辊半径。

（4）辊间弹性压扁影响函数。其表达式为：

其中，bwb为i单元辊间接触区宽度的1/2。

2.3 影响函数基本方程

用影响函数法计算轧机的弹性变形，共需要建立7个方程，其中4个力－变形关系方程、1个力平衡方程和2个变形协调方程［9］。

（1）力－变形关系方程。工作辊弹性弯曲方程为：

《春秋公羊传》虽成书于汉景帝之时，但早期公羊学自孔子作《春秋》之时便已存在，并经过孔子口授传至后代。[6]在战国，得圣人之初心的子夏对《春秋》的诠释就已经受学者推崇，《韩非子》中就多见引述。

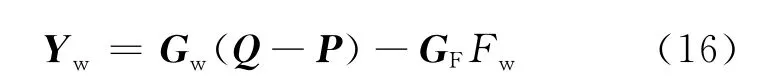
其中，Gw、Fw、GF分别为工作辊的弯曲影响函数矩阵、弯辊力及其弯曲影响函数矩阵，Gw＝［gw（i，j）］n×n。

支承辊弹性弯曲方程为：

其中，Gb分别为支承辊弯曲影响函数矩阵，Gb＝［gb（i，j）］n×n。

轧制压力引起的工作辊弹性压扁方程为：

其中，Yws、Gws分别为工作辊与轧件接触位置的单侧压扁量及压扁影响函数，Gws＝［gws（i，j）］m×m。

辊间弹性压扁方程为：

其中，Ywb、Gwb分别为工作辊与支承辊接触位置的单侧压扁量及压扁影响函数，Gwb＝［gwb（i，j）］n×n。

（2）力平衡关系方程。其表达式为：

（3）变形协调关系方程。工作辊与支承辊之间的变形协调关系方程为：

其中，Ywb0为中点处辊间压扁常量向量；Mw、Mb分别为工作辊、支承辊的凸度向量。

轧件与工作辊之间的变形协调方程为：

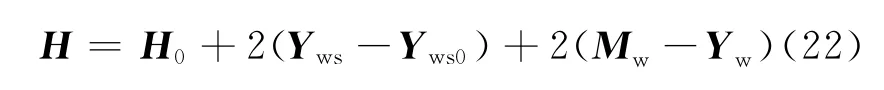
其中，Yws0为轧件与轧辊接触面辊面中心处的压扁常量向量；H、H0分别为轧后轧件厚度向量、板中心处厚度常量向量。

根据上述的基本方程编写迭代程序，程序框图如图2所示。其中ε1、ε2和ε3分别为辊间压力误差、工作辊静力平衡误差和轧件厚度误差收敛参数。

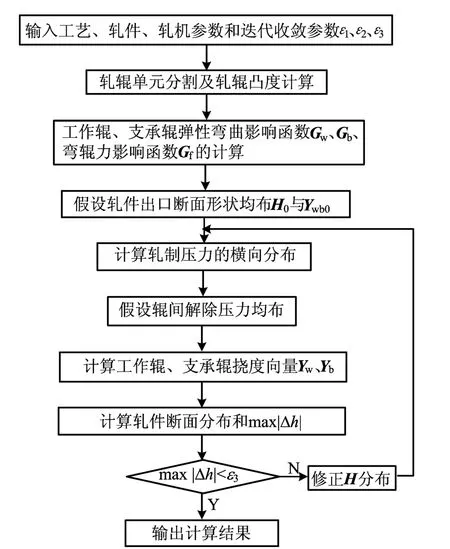
图2 辊系弹性变形计算框图

3 计算结果与讨论

为了验证影响函数法迭代计算的正确性，将某厂实测生产数据中的轧制压力与计算值进行比较，结果见表1所列。通过比较可以看出，影响函数法的迭代计算结果与实测值吻合较好，间接说明基于影响函数法迭代计算的横向厚度分布也较为准确。

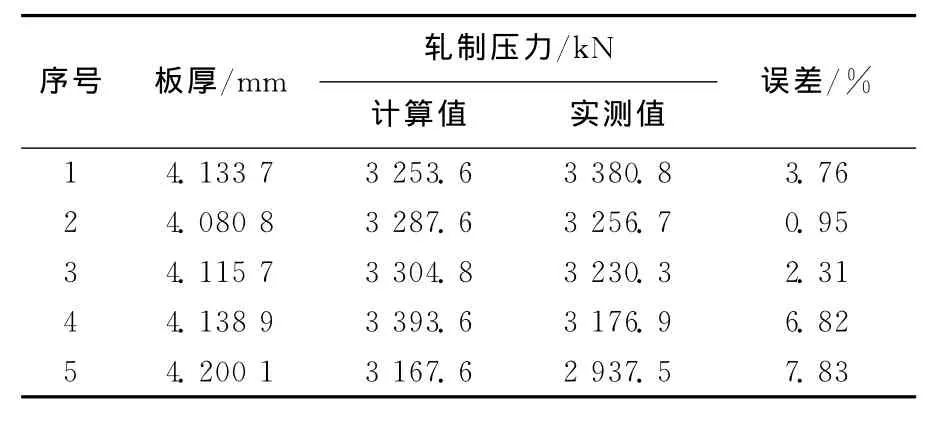
表1 计算值与实测值对比表

当弯辊力为16kN时，用影响函数法计算的板厚横向分布如图3所示，板厚横向分布与前张应力关系的对应曲线如图4所示。

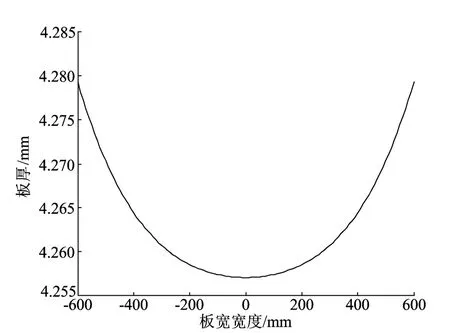
图3 基于影响函数法计算的板厚分布

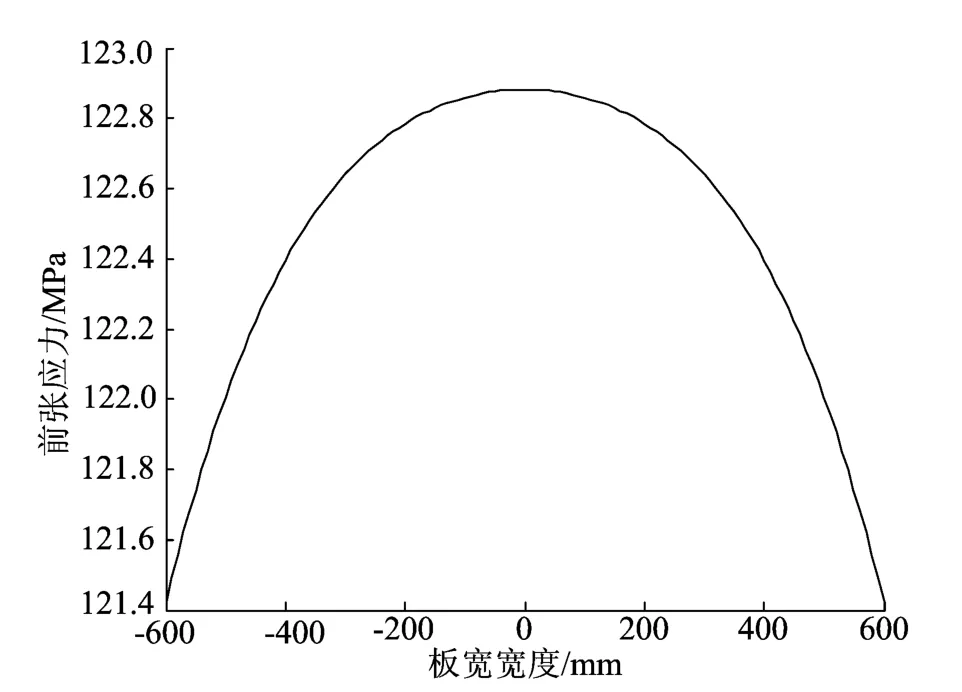
图4 前张应力分布与板厚分布对应关系

由图3可以看出，板宽中心处的厚度与边部厚度有明显的落差，这是由于轧辊受到弯辊力的作用，产生了弹性变形，轧辊辊颈处受到了较大的弯辊力作用，所以边部比中心处的厚度要大得多；由图4可以看出，前张力分布不均，边部受到的张力较小，产生的纵向变形量小于中心处纵向变形量，此时产生的板形缺陷为中浪，根据板宽横向分布的情况，可以推断板形产生了浪形缺陷。

4 实测板厚横向分布与板形的映射

为了说明通过横向厚度分布形式可以得出板形缺陷与板厚分布的映射关系，本文以某铝业公司现场采集到的实测板厚分布数据和实际的板形缺陷来验证以上理论的正确性。板厚横向分布测量点用六次函数拟合，拟合的曲线如图5所示。

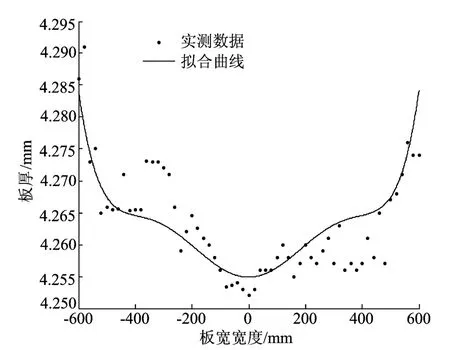
图5 实测厚度分布与拟合函数曲线

实测板厚分布对应的前张应力如图6所示。

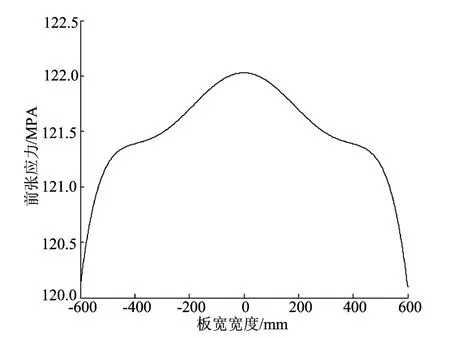
图6 实测板厚对应的前张应力曲线

根据前面所述理论，通过板厚横向分布的形式可以推测出此时的板形缺陷为中浪，实际测量板形的缺陷也为中浪，说明上述理论与实际情况吻合。

5 结论

（1）本文用影响函数法对辊系弹性变形进行计算和分析，收敛速度快，能满足快速计算的要求。

（2）根据前张应力与出口板形一一对应的关系，可以将板形用板厚横向厚度分布的特征进行映射。

（3）由于轧制生产线上缺少板形检测系统，只能测量横向断面多点厚度分布来表征板凸度，不能直接反映板形；本文可以根据板形与板横向厚度分布的映射特征，通过测量横向厚度分布值，为板形预测和控制提供理论依据。

［1］张志强.四辊冷轧机板带板形建模与分析［D］.太原：太原科技大学，2012.

［2］胡国栋，孙登月，许石民，等.冷轧带材前张应力分布、横向厚差与板形关系［J］.钢铁，1998，33（12）：62－64.

［3］陈连生.金属模型与变形模型耦合计算热轧板凸度［J］.河北理工学院学报，2002，24（2）：17－24.

［4］骆 拓，邓 华，赵世庆，等.基于影响函数法的轧制压力横向分布规律分析［J］.机械强度，2010，32（1）：165－170.

［5］Jiang Z Y，Zhu HT，Tieu A K.Effect of rolling parameters on cold rolling of thin strip during work roll edge contact［J］.Journal of Materials Processing Technology，2003，140（38）：535－541.

［6］孙一康.带钢热连轧的模型与控制［M］.北京：冶金工业出版社，2002：216.

［7］日本钢铁协会.板带轧制理论与实践［M］.王国栋，吴国良，译.北京：中国铁道出版社，1990：458.

［8］王国栋.板形控制和板形理论［M］.北京：冶金工业出版社，1986：293－294.

［9］骆 拓，邓 华，李凤轶，等.板宽对轧辊受力分布的影响规律［J］.机械设计与制造，2008（12）：200－202.