基于DBN-BP 深度算法的热轧板带横断面预测*

高山凤，刘美红，范秋霞

(山西大学 自动化与软件学院，山西 太原 030006)

0 引言

在钢铁及有色金属行业，轧制是目前最重要的板带材产品成材工序之一。随着市场对热轧产品以及冷轧产品质量要求的不断提高，热轧板带横断面形状越来越受到重视，其主要的评价指标有凸度、楔形、边降和局部高点等。同时热轧板带是冷轧板带的材料来源，现有研究表明热轧板带对冷轧板形的质量有着重要影响[1]。热轧工序常常需要根据冷轧需求控制板形，板形的质量控制已从冷轧的控制延伸到轧制全流程控制。

由于轧制过程中变形区金属发生三维塑性变形，存在明显的金属横向流动现象[2]，造成板带横断面形状难以准确预测。目前对板带横断面形状的研究主要是集中在板带凸度和边部减薄量的研究，研究方法有数学模型[3-5]、有限元[6-10]、轧机设备研发[11]和机器学习算法[12-14]等。虽然板带凸度能够用来粗略说明轧机对轧件横断面的改变能力，并可用来分析轧机对于板带边浪和中浪的控制能力，但对于具有复杂断面形状变化的轧件是无法单独使用板带凸度进行板形评价的[3]。此外，生产中为了保证板带的边部质量，往往必须将板带边部减薄部分裁切掉，而减小板带切边量是降本增效有效的方法[15-17]。

板带凸度和边部减薄量的研究对象均是板带横向局部点与中心点厚度的差值，而要对板带横断面形状进行综合控制，需要对板带横向多个关键点的厚度进行分析,也就是对板带横向厚度分布进行分析。板带横断面的主要研究方法有数学模型[18-19]、有限元法[20-21]和差分方法[22]。虽然数学模型计算效率高，易于实现，但是预测精度较低[19]；而有限元方法计算工作量较大，不适合在线分析使用。

为了提高板带横断面形状的预测精度与效率，以便提高其控制精度，本文采用数据挖掘技术对轧机系统的轧制参数进行采集与预处理，数据挖掘过程采用DBN-BP深度学习网络方法。

1 板带横断面影响因素分析

本文研究基础为二辊铝板带热轧机，影响热轧板带横断面形状的主要因素有：轧制速度、轧制力、工作辊热辊形、工作辊磨损、板带温度、压下量。其中，工作辊磨损与热辊形是影响板形横断面形状的主要因素，也是难以在线准确测量的参数，且两者均与轧制板带卷数(轧制时间)有关。

1.1 工作辊磨损计算模型

工作辊磨损导致初始辊形与辊缝形状的变化，进而影响板带轧制质量。对工作辊磨损量进行准确预测是提高板形预测精度与板形质量的关键因素。长期以来，国内外科研人员建立了一系列的轧辊磨损计算模型[23-26]，并且随着计算技术与数值计算方法的发展，轧辊磨损模型的计算精度也得到了提高。

在分析现有研究结果的基础上，轧制一卷铝板带时，二辊铝板带热轧机工作辊磨损量计算模型如下：

式中，i 为轧制道次；m 为一卷板带总的轧制道次；x 为工作辊轴向坐标；w(x)为x 位置处的半径磨损量，单位为μm；Liz为第i 道次的轧制长度，单位为km；pi为单位面积轧制压力，单位为MPa；lis为接触弧长，单位为mm；Dw为工作辊直径，单位为mm；k0为模型参数；k1为单位面积轧制压力影响指数；f(x)为描述轧辊轴向不均匀磨损程度的函数，计算模型如下：

式中，xc为板带中点对应的轧辊轴向坐标，单位为mm；Lw为工作辊辊身长度，单位为mm；ke、kp分别为边部、极值点的磨损系数；b2为多项式系数；d1、d2分别为板带边部以外的磨损和板带边部到极值点的距离；B 为板带宽度，单位为mm。

当轧制n 卷板带后，该热轧机工作辊的磨损总量为：

式中，j 为轧制板带数量。

在求解过程中，假设轧辊两侧磨损呈对称分布。工作辊辊身长900 mm，板带宽度为680 mm，轧制板带数量n 分别为数10、20 和30时，按照上述模型计算工作辊磨损分布以及磨损量，如图1 所示。

图1 工作辊磨损

1.2 工作辊热辊形

工作辊热膨胀量在线测量较难，但是工作辊的热膨胀量的大小与工作辊表面温度有关。为了准确地获得轧辊温度，该轧机配有温度检测系统，其工作原理为采用扫描式的红外温度检测方法，红外传感器安装在检测装置中，检测装置可以沿轴向移动，通过控制系统可以设定温度检测点的位置。现场安装如图2 所示，测温装置安装在上轧辊的上面。经过试验测试结果可知该轧辊温度的测量误差为±1 ℃。

图2 轧辊测温装置安装实物图

2 神经网络模型

2.1 BP 算法

BP 神经网络是一种多层前馈神经网络，该网络的主要特点是信号前向传递，误差反向传播。在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层。其中每一层的神经元只影响下一层的神经元状态。如果在输出层的网络输出与所期望的输出误差增大，则转入到反向传播，根据预测误差反向调整网络所有的权值和阈值，使误差信号最小。

BP 算法是有监督的学习模型，对于网络初始值的选择要求较高，由于初始值选择不合理，将会导致算法陷入局部最优。

2.2 RBM 算法

典型的RBM 模型由可见层和隐藏层组成，通过能量函数定义其联合概率。RBM 的能量函数可定义为：

式中，a、b 分别是可见层v 和隐藏层h 的偏置；w 为权值矩阵；v、h 分别表示可见层与隐藏层向量。

θ={w，a，b}为RMB 中的参数，其联合概率分布为：

由式(6)得到输入层和隐含层的概率分布为：

RMB 节点的状态为激活(1)或抑制(0)两种状态，其可见层单元激活函数和隐藏层单元的激活函数可表示为：

采用对比散度算法(Contrastive Divergence，CD)，通过式(9)和式(10)对可视层和隐藏层进行重构，更新参数θ。

2.3 DBN-BP 网络模型

DBN 模型由多层RBM 组成，通过贪婪无监督学习模式逐层训练堆叠的RBM，而DBN 学习得到权重矩阵和偏移量，供BP 网络训练使用；同时，利用误差反向传播对参数进行微调，并建立预测目标的模型。DBN 作为一种概率生成模型可使网络按照最大概率生成训练数据。

DBN-BP 的模型结构如图3 所示，DBN-BP 网络的运算步骤为：

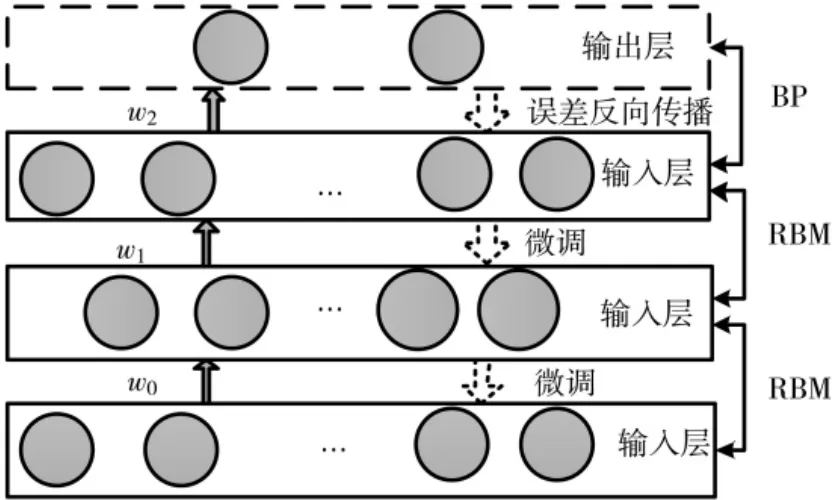
图3 DBN-BP 模型结构

(1)训练过程：利用对比散度算法(CD 算法)逐层训练RBM，训练集数据作为最底层RBM 的可见层的输入，通过计算得到其隐藏层向量，并将该层的权值矩阵和偏置输入到下一层RBM。重复该过程，直到最后一层RBM，完成多层RBM 的无监督训练过程，得到参数θ={w，a，b}。

(2)微调过程：最后一层的RBM 输出的权值矩阵和偏置作为BP 算法对的输入，进行有监督的学习；经过计算后，BP 网络将误差反向传播，在调整网络参数的同时，完成对各层RBM 微调的过程。

在训练的过程中，每一层RBM 网络的模型参数只是自身层内的最优值，并非全局最优；但是，经过BP 算法将误差反向传播，自顶向下传播至每一层的RBM，微调整个DBN 网络，从而使模型收敛到全局最优解。该过程可以看作对一个深层BP 网络权值参数的初始化，使DBN 克服了BP 网络因随机初始化权值参数而陷入局部最优和训练时间长的缺点。

假设网络训练的目标函数为平均误差E，如下所示：

3 预测模型与结果分析

3.1 实验数据来源

为了研究不同轧制产量时板带横断面的预测精度；连续采集15 天稳定轧制过程中的轧制参数与板带厚度(每天前6 卷板带)，并选取每组的20%的数据作为测试数据。同时，选取轧制力(F)、轧制速度(v)、工作辊温度(Ti)、板带入口温度(Tsi)、工作辊磨损(Ui)和压下量(h)作为输入参数，输出为板带横向各点的厚度(Hi)，其中i=1～9。其中各点对应处的工作辊磨损量由本文所述计算方法得出，工作辊的热膨胀由实测的工作辊表面温度表示。

此外，由于板带凸度一般是距离边部40 mm 处板带厚度与中心厚度的差值，边降一般为边部15 mm 处板带厚度与中心厚度的差值，因此，本文板带宽度为680 mm时，设定9 个板带厚度的观测点，分别为板带两侧距离板带中心距离为130 mm、230 mm、300 mm、325 mm 和中心点等位置处的厚度，并从传动侧至操作侧顺序编号。

由于本文采用的是多输入模型，为消除量纲影响，缩小取值范围，避免数值过大影响最终结果，需要对样本数据进行归一化处理，将其映射到[0，1]之间，公式如下：

式中，x 为样本数据，xmax为样本数据的最大值，xmin为样本数据的最小值。

3.2 结果分析

分别采用BP 算法、DBN-BP 算法预测板带横向各点厚度，图4 所示为其中一卷终轧道次稳定轧制时板带厚度的预测值与测量值，其平均绝对误差分别为7.8 μm 和4.1 μm。经统计，采用DNB-BP 预测终轧道次稳定轧制时板带中心点厚度误差在±5.6 μm 内的概率可达到95%，而BP 算法的预测误差范围为±11 μm。

图4 板带中点厚度预测值与测量值的误差

图5 为分别采用BP 算法和DBN-BP 算法预测各点板带厚度，从而得到的板带横向断面形状。由图可知DBN-BP 的预测精度较高，尤其板带边部厚度的预测精度高于BP 神经网络的预算精度。

图5 板带横断面形状

为了说明轧制过程不同轧制时间板带厚度预测精度，图6 所示为按照板带的轧制顺序终轧道次板带厚度预测的平均绝对值误差。由于工作辊内部温度与热膨胀需要一定的轧制时间才能到达稳定状态，导致开轧的前两卷板带的预测精度较低；同时，由于板带边部厚度变化与工作辊磨损机理等情况复杂，导致边部厚度的预测精度低于中心区域各点板厚的预测精度。

图6 板带厚度预测误差

4 结论

为了高效、准确地控制热轧板带横断面形状，本文采用DBN-BP 神经网络建立其预测模型，并得出相关结论如下：

(1)随着机器学习算法的发展，深度学习逐渐被应用到各工业领域；在分析板带横断面形状影响因素以及建立二辊轧机工作辊磨损计算模型的基础上，采用DBN-BP 深度网络学习算法，建立板带横向不同点厚度的预测模型。通过对比可知，采用BP 算法和DBN-BP 算法进行板带厚度的预测，板带中心点厚度的误差范围分别为±11 μm 和±5.6 μm。

(2)板带开轧时，工作辊内部温度未达到稳定状态时，板带厚度预测精度较低；对于同一板带，板带边部预测精度较低。为进一步提高板带横断面形状预测精度，需要对上述两种情况下的预测精度进行进一步的研究。