单站无源定位中相位差变化率的高精度提取

侯建民，靳学明，齐美彬

（1.合肥工业大学 计算机与信息学院，安徽 合肥 230009；2.中国电子科技集团公司 第三十八研究所，安徽 合肥 230088）

0 引言

无源定位技术是电子侦察中一项非常重要的技术。其原理是观测站不发射信号，只被动接收目标辐射源的信号对目标进行定位。其中单站无源定位［1－3］由于只有1个观测站，具有设备小、隐蔽性好、不需要复杂的同步等优点，在现化战争中的生存能力更强，应用前景更加广阔，已逐步成为当今国内外研究的热点。

基于相位差变化率的单站无源定位技术［1－8］是一种基于运动学原理的新颖的定位方法，与传统的定位方法相比具有定位精度高、定位速度快等优点，近年来得到了高度重视和快速发展。由于该方法主要利用相位差变化率来对目标进行定位，所以相位差变化率是一个非常重要的参数，提高定位精度首要任务就是提高相位差变化率的精度。相位差变化率的获取一般有直接测量和间接提取2种途径。直接测量是利用一些硬件设备对接收到目标辐射源信号直接进行处理来获取目标信号的相位差变化率。文献［9－10］提出了一种模拟测量和数字测量方法。实际上，相位差变化率的直接测量对设备要求比较高，且通道间的干扰、放大器、A/D转换器、测频器等设备的噪声都会严重影响相位差变化率的测量精度。

目前最常用的是利用间接提取的方法来获取相位差变化率。其思想是先利用干涉仪对相位差进行测量，然后再通过一定的算法计算出其变化率。常用的间接提取方法有差分法、卡尔曼滤波法、线性拟合法、α－β滤波法等。文献［6，11］介绍了差分法、卡尔曼滤波法以及线性拟合法的基本原理，并对提取效果进行了分析对比，结果表明卡尔曼滤波法提取精度高于其他2种方法。文献［12］对比分析了差分法、卡尔曼滤波法、α－β滤波法3种方法，并证明了卡尔曼滤波法的提取精度高于α－β滤波法。

综上所述，卡尔曼滤波法是4种方法中提取相位差变化率精度最高的，但对初始值比较敏感，随着相位差测量误差的增大，其提取精度会有明显减小，且有可能出现发散现象。文献［13］提出了一种利用时间片求取相位差变化率的方法，该方法在一定程度上提高了相位差变化率的精度，但在观测过程中相位差的变化接近线性时，提取精度仍然没有卡尔曼滤波法高。

针对以上方法的不足，为了进一步提高相位差变化率的提取精度，本文提出了时间片差分卡尔曼法来提取相位差变化率。该方法避免了卡尔曼滤波法中直接利用干涉仪获得的相位差作为输入来求取相位差变化率，而是采用了二次提取。首先延长每次的观测间隔，引入时间片对差分法进行改进，提取到一定精度的相位差变化率，然后将提取到的相位差变化率作为输入用卡尔曼滤波器进行平滑去噪，实现对相位差变化率的高精度提取。

1 相位差变化率的分析

假设机载观测平台相对于固定目标作非径向的匀速直线运动，且飞机的飞行姿态不发生变化。以固定目标位置为坐标原点O，建立三维直角坐标系载机的飞行轨迹如图1所示。

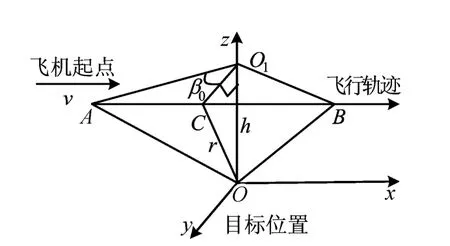
图1 载机的飞行轨迹

图1中，飞机沿x轴正向作匀速直线运动，且飞行速度为v；O1为目标在观测平台水平面的投影；A点为机载观测平台的观测起点；B点与A点相对于y轴对称；C为AB的中点，且OC⊥AB，即OC为飞机与目标截距r；h为飞机的飞行高度；β0为起始观测方位角，由几何关系可得飞机观测起点A的坐标为

由载机接收目标信号示意图［14］及定位原理可知，在某一时刻i，目标与观测平台的径向距离ri为：

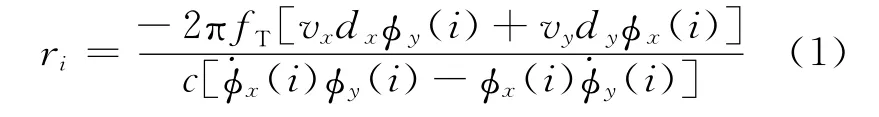
结合径向距离和方位角、俯仰角即可求出目标的坐标值，实现对目标的实时定位。

为了更直观地反映出相位差变化率对定位结果的影响，在图1所示的飞行轨迹下，设定相关的参数如下：r＝200km，h＝10km，β0＝30°，v＝300m/s，dx＝dy＝10m，fT＝3×109Hz。在其他参数测量误差不变的前提下，取不同相位差变化率误差δ˙φ，以定位点与真实点的偏差距离为指标对定位结果进行仿真实验，仿真结果如图2所示。

由图2可看出，当相位差变化率的误差变为原来的2倍时，定位点与真实点的偏差距离也变为原来的2倍。定位精度与相位差变化率的精度成正比，所以提高相位差变化率的精度是提高定位精度的关键。

相位差变化率实际上为相位差随时间的变化频率，因此相位差变化率可以通过频率的克拉美－罗下限（Cramér－Rao low bound，CRLB）［9］来确定。单载波复信号的相位差变化率CRLB定义为：

其中，观测时间T1＝NTs；N为采样数；Ts为采样间隔；SNR为信噪比。

从（2）式可以看出，相位差变化率的方差随SNR、T1、N成反比变化，特别地，与观测时间T1成平方指数变化。所以观测时间越长的方差越小，测量精度越高。这意味着增加观测时间可以有效地提高相位差变化率的测量精度。这是因为在一个观测时间段内的变化非常小以至于可以近似看作是不变的，延长每次的观测时间后，每次观测都可以得到一系列的相位差，可以有效地减小误差的影响。

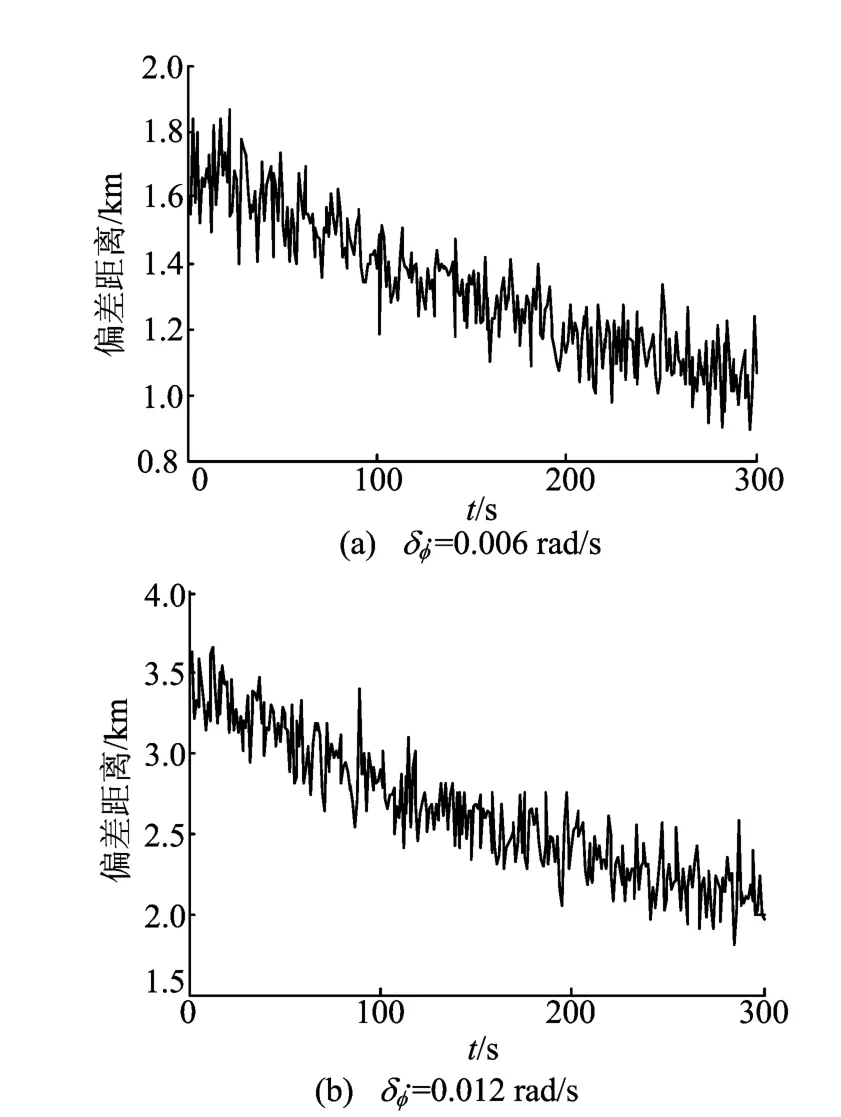
图2 不同δ˙φ值时定位点与真实点的偏差距离

2 本文算法提取相位差变化率

提高定位精度的关键是提高相位差变化率的精度，本文提出采用时间片差分卡尔曼法来提取相位差变化率。算法的基本思想是利用干涉仪测量目标信号的相位差，对提取到的相位差以固定时间间隔进行观测；根据相位差变化率的CRLB分析，增加观测时间可以提高相位差变化率的精度，所以本文延长了每次观测时间，使得每次观测都可以得到多个相位差值，形成一个时间片，则多次观测可以得到多个时间片。取相邻2个时间片联合求取相位差变化率，实现对相位差变化率的初步提取，然后再经过卡尔曼滤波对提取到的相位差变化率进行平滑去噪，进一步提高其精度，最终实现对相位差变化率的高精度提取。

2.1 相位差的测量

假设从目标辐射源接收的信号是恒定频率的正弦相干脉冲序列，表达式为：

其中，t为时间；AT为恒定的脉冲幅度；θ0为初始相位；Tr为脉冲重复间隔；k为非负整数，且

其中，脉冲宽度τ≪Tr。

利用干涉仪测量相位差原理如图3所示。

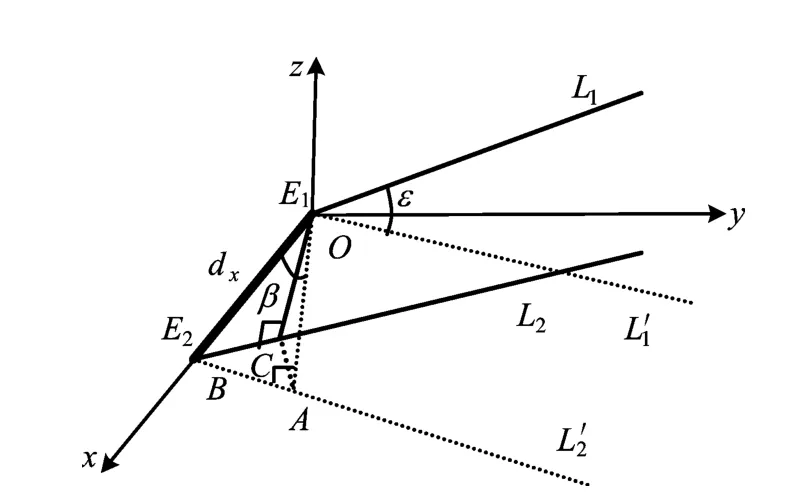
图3 干涉仪测量相位差原理图

图3中，E1、E2为x轴上干涉仪两天线，E1位于坐标原点O，E2位于B点；dx为干涉仪基线长度，即OB＝dx；L1、L2为辐射源信号；L1′、L2′为L1、L2在xOy平面的投影，过坐标原点O作L2的垂直线相交L2于C点，过O点作L2′的垂直线相交L2′于A点。则BC段的长度即为信号到达两天线的距离差Δs。由几何关系可知：

故

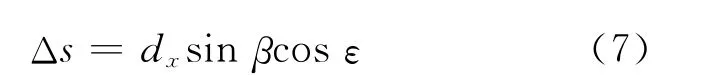
两天线接收信号的时间差为：

则相位差的表达式为：

实际上，由于一维干涉仪只能测（－π，π）的相位差，当干涉仪的基线长度d＞λ/2时，测量得到的相位差很有可能会产生相位模糊，会严重影响相位差变化率的提取精度。可以通过一些解模糊方法处理，如利用参差距离解模糊［15］可得无模糊的相位差序列。

2.2 相位差变化率的初步提取

以固定观测间隔T观测记录干涉仪得到的相位差，延长每次的观测时间，可以得到1个相位差序列，把1次观测所占用的时间称为1个时间片。经过N次观测，可以得到N个时间片，每个时间片包含M个相位差值。依次取相邻2个时间片，将第i个时间片内的M个相位差与第i－1个时间片内对应的M个相位差依次作差，如图4所示。

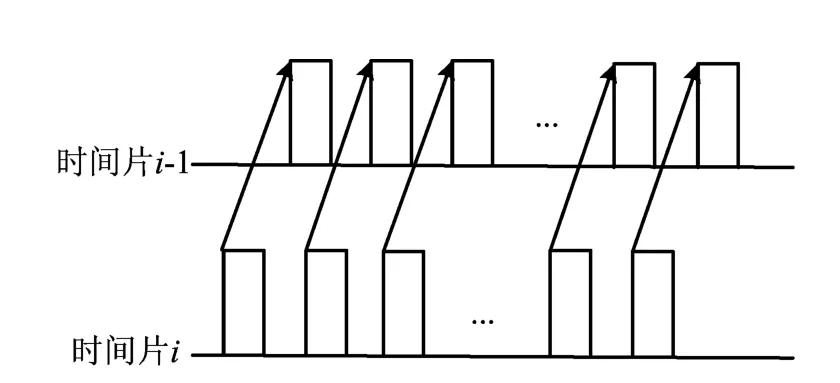
图4 相邻2个时间片求取相位差变化率

则由以上分析可得：

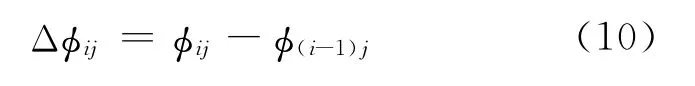
其中，i＝2，3，…，N；j＝1，2，3，…，M。

将2个时间片内得到的所有Δφij取平均后除以时间间隔T近似作为第i个时间片（即第i次观测）的相位差变化率，即

取其对应的时间点为本次观测的开始时刻。依此类推，可以得到一个包含有N－1个相位差变化率的序列，实现了对相位差变化率的初步提取。

2.3 相位差变化率的二次提取

将相位差变化率作为观测变量，将相位差变化率及其变化的加速度作为状态变量进行卡尔曼滤波，进一步提高相位差变化率的提取精度。

已知卡尔曼滤波要求其状态方程与观测方程都为线性。本文忽略误差，在图1所示的飞行轨迹下对相位差变化率及其变化的加速度曲线进行仿真，结果如图5所示。

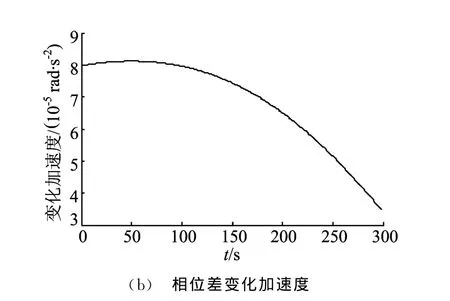
图5 相位差变化率及其加速度真实值

从图5可以看出，相位差变化率与相位差变化加速度近似成线性变化，满足卡尔曼滤波要求。

状态方程为：

观测方程为：

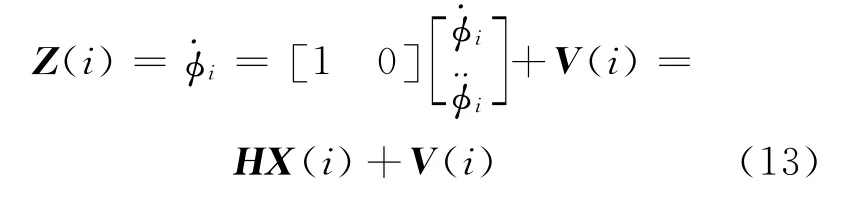
其中，A为状态转移矩阵；H为观测矩阵；W（i）为系统噪声；V（i）为观测噪声。设所有噪声都为均值为0的高斯白噪声。

通过卡尔曼滤波方程可求得相位差变化率的值。卡尔曼滤波方程为：

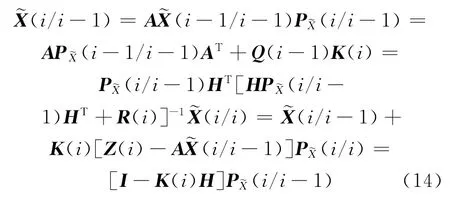
其中，Q（i）为系统噪声协方差；R（i）为观测噪声协方差。

相位差变化加速度的初值可以用得到的相位差变化率通过两点差值法来确定。

3 实验结果及分析

在图1的载机飞行轨迹下，考虑实际情况以及现有设备，设定相关的参数为：r＝200km，h＝10km，β0＝30°，则由A点坐标公式可得飞机的起始位置为（－155.3，199.7，10），v＝300m/s，dx＝dy＝10m，fT＝3×109Hz，t＝1s。卡尔曼滤波方程中相关参数如下：

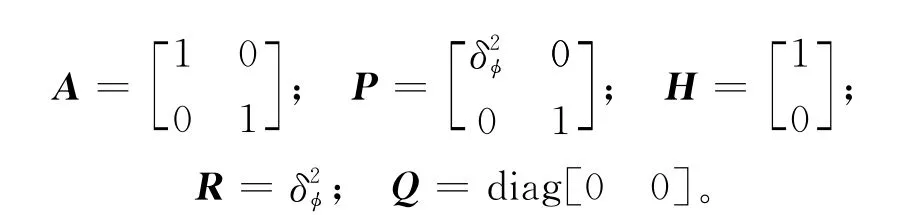
取已解模糊的相位差误差δφ＝10°，应用时间片差分卡尔曼法来提取对应的相位差变化率，并与卡尔曼滤波法、文献［13］的方法进行对比。本文以提取的相位差变化率的平均误差为指标对3种方法进行对比分析，由于设定的测量噪声为随机产生的高斯白噪声，为了排除偶然性，进行10次仿真，取10组平均误差值。每次仿真时均进行500次蒙特卡洛实验。相位差变化率的平均误差表达式为：

对δφ＝10°＝0.175rad进行仿真，仿真结果如图6所示。

3种方法的相位差变化率的平均误差值的对比结果见表1所列。

图6 δφ＝10°时的仿真结果

表1 δφ＝10°时˙δ的对比结果 rad/s

从图6a可以看出，时间片差分卡尔曼法可以有效地提取到相位差变化率，且提取精度较高；从图6b可以看出，卡尔曼滤波法和时间片差分卡尔曼法的提取精度均高于文献［13］方法的提取精度，但这2种方法对比不明显；从图6c可以看出，时间片差分卡尔曼法的提取精度要明显高于卡尔曼滤波法。

由表1可知，时间片差分卡尔曼法提取相位差变化率的平均误差要远小于文献［13］的方法和卡尔曼滤波法。实验结果表明，时间片差分卡尔曼法能正确地提取相位差变化率的值，是一种有效的高精度提取相位差变化率的方法。

时间片差分卡尔曼法也有其缺点。由于该方法是先利用二次提取方法，其提取时间会比其他几种方法有所延长，对定位的实时性有一定的影响。但由于其高精度性，在定位初期可以达到比较好的定位结果，而其他提取方法虽然提取相位差变化率的时间短，但由于提取误差大，定位初期的结果误差也大，需要经过一定时间的收敛，才可以达到好的定位结果。从这一方面来讲，对其提取时间长的缺点有所弥补。

4 结束语

本文对基于相位差变化率的单站无源定位中相位差变化率进行了研究，并分析了相位差变化率对定位结果的影响，发现其提取精度与定位精度成比例变化，是影响定位精度的最大因素。为了提高其提取精度，提出了一种新的提取相位差变化率的方法，即时间片差分卡尔曼法，并在不同的相位差测量误差下与文献［13］方法、卡尔曼滤波法2种提取方法进行了对比分析，通过仿真实验验证了该方法可以有效地提高相位差变化率精度。

［1］郁春来，张元发，万 方.无源定位技术体制及装备的现状与发展趋势［J］.空军雷达学院学报，2012，26（2）：79－85.

［2］Xu Tianyuan，Liu Shunlan.Single observer passive location using phase rate of change with the extended Kalman Particle filter ［C］//2009ISECS International Colloquium on Computing，Communication，Control，Management（VolumeⅢ），2009：65－68.

［3］Xi W，Yu B Z，Wang S S.Theoretical analysis of direct－finding targets with rolling－airframe passive radar by phase interference technique［C］//Proceedings of 2006CIE International Conference on Radar.International Colloquium：Chinese Institute of Electronics（CIE），2006：1－4.

［4］黄登才，丁 敏.测相位差变化率无源定位技术评述［J］.现代雷达，2007，29（8）：32－34.

［5］单月晖，孙仲康，皇甫堪.变化姿态下角相位差变化率无源定位方法研究［J］.电子学报，2002，30（12）：1897－1900.

［6］朱伟强，黄培康，马 琴.基于相位差变化率测量的单站定位方法［J］.系统工程与电子技术，2008，30（11）：2008－2011.

［7］郭福成，贾兴江，皇甫堪.仅用相位差变化率的机载单站无源定位方法及其误差分析［J］.航空学报，2009，30（6）：1090－1095.

［8］王强，钟丹星，郭福成，等.仅用长基线干涉仪测量相位差变化率的运动单站无源定位方法［J］.信号处理，2009，25（8A）：566－569.

［9］邓新蒲，祁颖松，卢启中，等.相位差变化率的测量方法及其测量精度分析［J］.系统工程与电子技术，2001，23（1）：20－23.

［10］万方，丁建江，郁春来.一种雷达脉冲信号相位差变化率测量的新方法［J］.系统工程与电子技术，2011，33（6）：1257－1260.

［11］杨晶，夏韶俊，吴伟.单站无源定位中相位差变化率的测量方法研究［J］.航天电子对抗，2013，29（3）：39－42.

［12］单月晖.空中观测平台对海面慢速目标单站无源定位跟踪及其关键技术研究［D］.长沙：国防科学技术大学，2002.

［13］Wang J H，Wang Y S，Guo T，et al.Rate of phase difference change estimation in single airborne passive locating system ［J］.Chinese Journal of Aeronautics，2009，22（2）：184－190.

［14］Shan Y H，An W，Sun Z K，et al.Passive location method based on phase rate of change ［J］.Chinese Journal of Aeronautics，2002，15（1）：49－54.

［15］龚享铱，袁俊泉，孙晓昶.基于参差距离的相位差变化值的解模糊方法研究［J］.信号处理，2003，19（4）：308－311.