幂级数逐项求导或积分后收敛半径不变的新证法

宋述刚，陈洋洋，邹健　(长江大学信息与数学学院，湖北 荆州 434023)

曾祥洲　(江陵县第一高级中学，湖北 江陵 434100)

幂级数逐项求导或积分后收敛半径不变的新证法

宋述刚，陈洋洋，邹健(长江大学信息与数学学院，湖北 荆州 434023)

曾祥洲(江陵县第一高级中学，湖北 江陵 434100)

[摘要]运用数列极限的理论建立了关于数列上、下极限的相关命题,应用该命题和Cauchy-Hadamard定理的逆定理,给出了幂级数逐项求导、逐项积分后所得新的幂级数和收敛半径不变的性质的一个新的证明方法。该证明方法较传统的证明(基于Abel定理与正项级数的比较判别法)更为简洁。上述关于实幂级数结论的证明方法,可以推广到复幂级数上去。

[关键词]上极限;下极限;幂级数;收敛半径

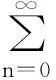
引理1

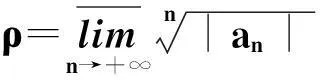
或

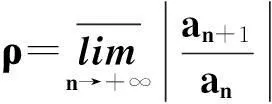
则:

注：当ρ=0时，R=+∞，ρ=+∞时，R=0。

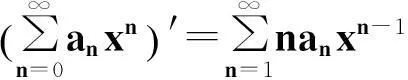
(1)

(2)

且有如下结论：

定理1

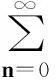
关于这一性质的证明，教材上一般都是基于Abel定理与正项级数的比较判别法[1~4]。下面，笔者通过建立数列上、下极限的相关命题，利用Cauchy-Hadamard定理的逆定理,给出了定理1的一个新证明。

1数列上下极限的相关命题

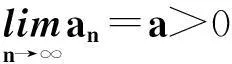
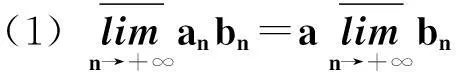
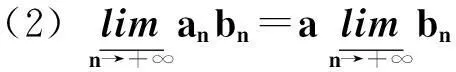
证明仅证第1个结论，第2个结论类似可证。

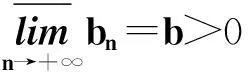
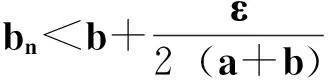
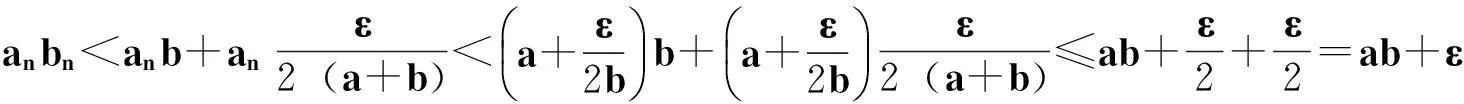
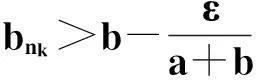
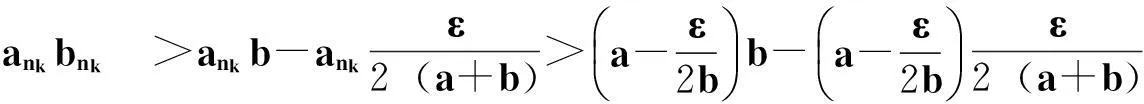
综合(i)、(ii)可得：

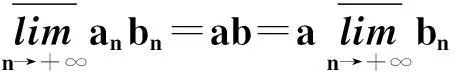
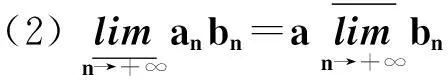
证明仅证第1个结论，由命题1有：

故命题2第1个结论得证。同理可证第2个结论。

例1计算下列极限：

解(1)由命题1第1个结论,有：

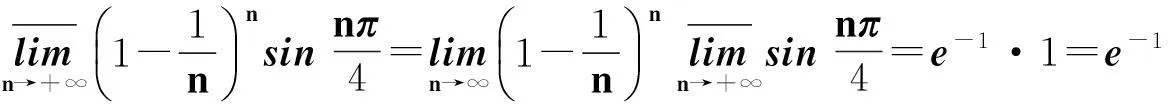
(2)由命题1第2个结论，有：

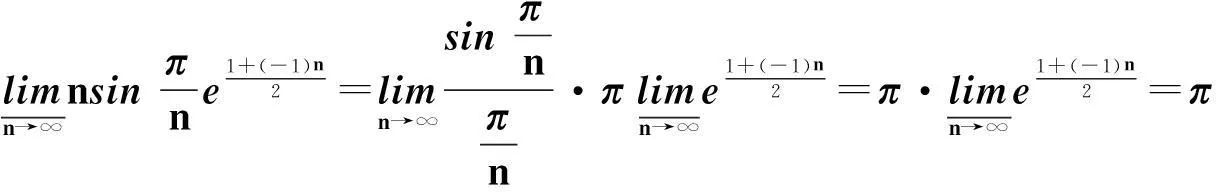
2Cauchy-Hadamard定理的逆定理

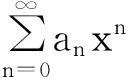
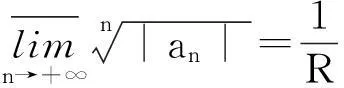
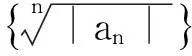
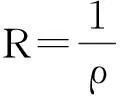
3定理1的新证明方法

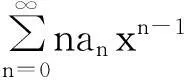
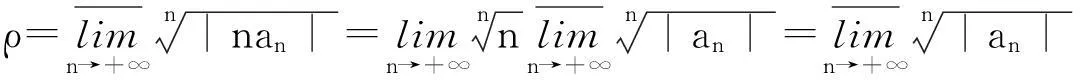
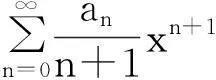
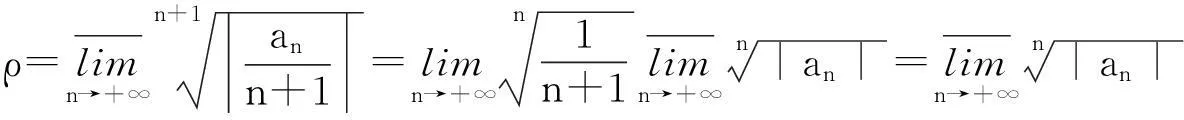
4结语

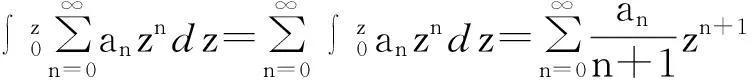
且它们的收敛半径不变。这一结论也可以利用定理1的新证法类似证明。

[参考文献]

[1]华东师范大学数学系.数学分析(上、下册)[M].第4版.北京:高等教育出版社，2010.

[2]菲赫金哥尔茨.微积分教程[M].北京大学高等数学教研室译.北京：人民教育出版社，1954.

[3]陈纪修，於崇华，金路.数学分析(上、下册)[M]. 第2版.北京:高等教育出版社，2004.

[4]常庚哲.数学分析教程[M].北京:高等教育出版社，2003.

[编辑]洪云飞

[引著格式]宋述刚，陈洋洋，邹健，等.幂级数逐项求导或积分后收敛半径不变的新证法[J].长江大学学报(自科版)，2015,12(28)：5~7.

[中图分类号]O171.2

[文献标志码]A

[文章编号]1673-1409(2015)28-0005-03

[作者简介]宋述刚(1961-)，男，教授，现主要从事函数论及数学史方面的教学与研究工作；E-mail:songsg@yangtzeu.edu.cn。

[基金项目]国家自然科学基金项目(61503407)；长江大学教学研究项目(YZ2014007)。

[收稿日期]2015-06-24