二元幂级数的收敛性
2018-03-10郭志华秦小雨曹怀信
郭志华,秦小雨,曹怀信
(陕西师范大学数学与信息科学学院,西安710119)
幂级数是数学分析的重要概念之一,在级数理论中具有极其重要的地位。关于一元幂级数的概念、收敛性及和函数等性质已有一套成熟的理论[1],而对于多元幂级数的相关概念和性质研究甚少。多项式函数是一类结构简单、性质良好的函数类,在基础数学与计算数学中具有重要应用[2-3]。在文献[4]中,笔者引入了多元函数项级数的概念,给出了其收敛域及和函数的定义,通过详实的例子讨论了多元幂级数的收敛域、和函数及多元函数展开为多元幂级数的计算方法。文献[5]讨论了二元幂级数收敛半径的计算公式,但没有明确给出二元幂级数收敛半径的定义。文献[6]讨论了一个关于SP(n)的无穷级数的收敛性问题,文献[7]研究了关于幂级数在自然数列中的应用。
本文根据一元幂级数相关原理,通过探究二元函数项级数的概念及收敛性,引出二元幂级数及其收敛半径等概念,给出收敛半径的相关性质,证明一些收敛和绝对收敛性定理,并以实例给出求解收敛半径的方法。
1 二元函数项级数
1.1 二元函数项级数的概念
设{un(x,y)}是定义在区域D上的一个函数列,称表达式


为函数项级数(1)的部分和。
1.2 二元函数项级数的收敛性
定义1 若点P0=(x0,y0)∈D使得数项级数

收敛,即当n→∞ 时,部分和

的极限存在,则称二元函数项级数(1)在点P0=(x0,y0)收敛,且称点P0=(x0,y0)为级数(1)的收敛点;若级数(3)发散,则称级数(1)在点P0=(x0,y0)发散。若级数(1)在D的某个子集H上每一点都收敛,则称级数(1)在H上收敛。若H为级数(1)全体收敛点的集合,则称H为级数(1)的收敛域。此时,级数(1)在H上每一点P=(x,y)与其所对应的数项级数(3)的和S(x,y)构成一个定义在H上的函数,称为级数(1)的和函数,并写作

即
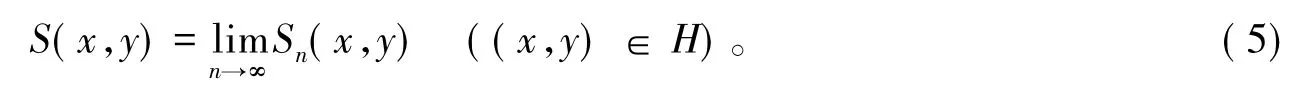
2 二元幂级数
2.1 二元幂级数的概念

称其为一个二元幂级数,其中常数

称为该幂级数的系数。由定义知
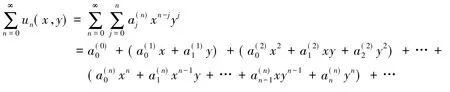
例如,当
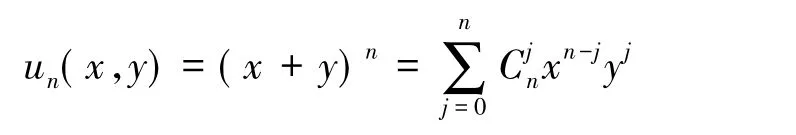
时,相应的二元幂级数为
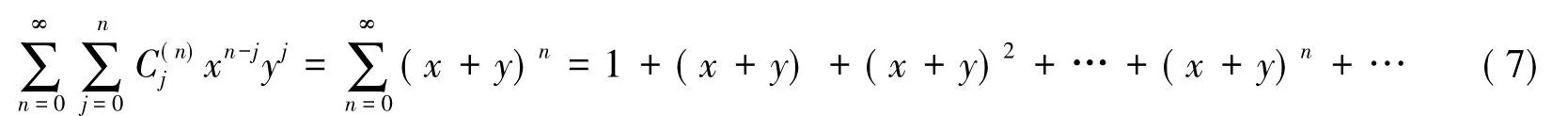
2.2 二元幂级数的收敛性
类似于一元幂级数的收敛性定理,我们有下面关于二元幂级数的收敛性定理。
定理1 (1)若二元幂级数(6)在点P0=(x0,y0)≠(0,0)收敛,则当

时,二元幂级数(6)收敛且绝对收敛;
(2)若二元幂级数(6)在点P0发散,则当
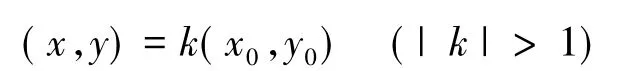
时,二元幂级数(6)发散。
证明 (1)因为二元幂级数(6)在点P0=(x0,y0)≠(0,0)收敛,所以

收敛,从而当n→∞ 时,通项un(x0,y0)收敛于0。于是,存在常数M >0,使得
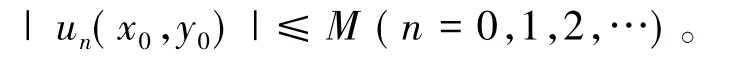
于是,当
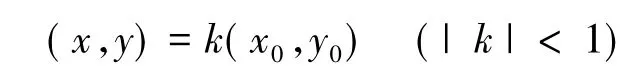
时,有

(2)由结论(1)可知。
推论1 若二元幂级数(6)在某个圆周Cr:x2+y2=r2(r>0)上的每个点处都收敛,则它在该圆内处处绝对收敛。
证明 设P=(x,y) 为圆周Cr内的任一点,则它可表示为(x,y)=k(x0,y0)(|k| < 1),其中:(x0,y0)∈Cr。从而,由定理1知二元幂级数(6)在P=(x,y)处绝对收敛。
基于这个推论,我们引入二元幂级数(6)的收敛半径的概念。
定义3 称

为二元幂级数(6)的收敛半径。
例1 对于二元幂级数(7),由于

所以,由根式判别法知:当|x+y|<1时,二元幂级数(7)绝对收敛;当|x+y|>1时,二元幂级数(7)发散。因此,其收敛半径同时,当|x+y|=1时,二元幂级数(7)的通项不收敛于0,从而级数发散。故二元幂级数(7)的收敛域为,如图1所示。
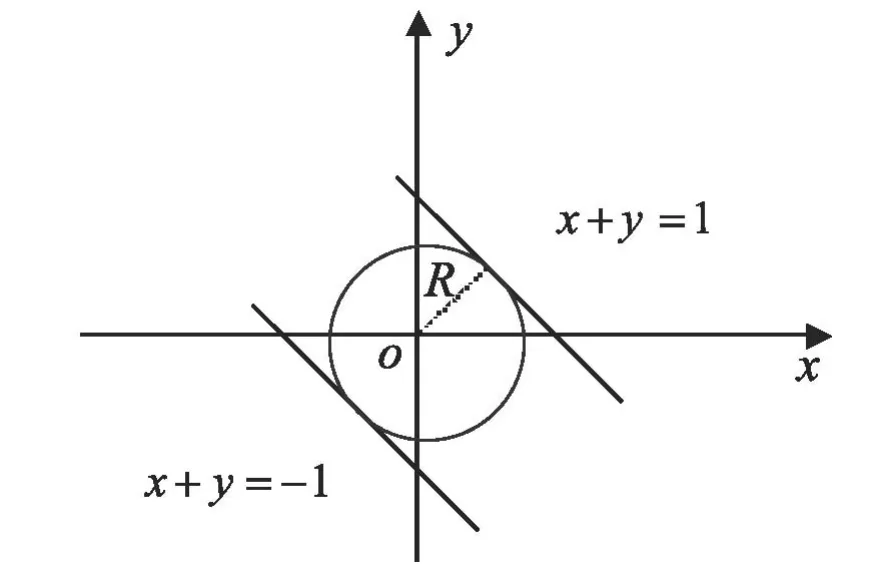
图1 |x+y|=1的图像及收敛半径R,收敛域为两条直线围成的无界开域
下面给出收敛半径的意义。
定理2 (1)当R=0时,二元幂级数(4)的收敛域不能完全包含任何以原点为中心的圆周;(2)当R→+∞时,二元幂级数(6)在整个平面处处绝对收敛;(3)当0<R<∞时,二元幂级数(6)在圆CR:x2+y2=R2内处处绝对收敛;在圆CR:x2+y2=R2外,至少一点处发散。
证明 (1)由收敛半径的定义可知。
(2)当R→+∞时,由收敛半径的定义知:存在一个趋近于正无穷大的正数列{rn},使得在圆周Crn:x2+y2=上,二元幂级数(6)处处收敛。对于任何圆周Cr:x2+y2=r2(r>0),当n足够大时,有rn>r。于是,根据推论1知二元幂级数(6)在圆Cr上处处绝对收敛。由r的任意性可知:二元幂级数(6)在整个平面处处绝对收敛。
(3)设P=(x,y)为圆周CR内任一点,则x2+y2<R2。由收敛半径的定义知:存在正数列{rn}使得rn→R(n→∞)且二元幂级数(6)在Crn上的每个点都收敛。取充分大的自然数n,使得R2。由推论1知二元幂级数(6)在点P=(x,y)处绝对收敛。
注1 当R=0时,二元幂级数(6)可能在除了原点之外的点处收敛。
推论2 对于二元幂级数(6),记

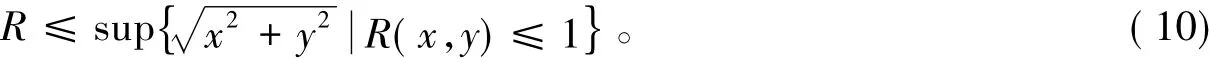
注2 对于例2中的幂级数,有u2n(x,y)=n!xnyn,u2n+1(x,y)=0,a→+∞,但R=0。这说明不等式(10)中的小于号是可以成立的。对于二元幂级数,有u2n(x,y)=(x2+y2)n,u2n+1(x,y)=0,从而
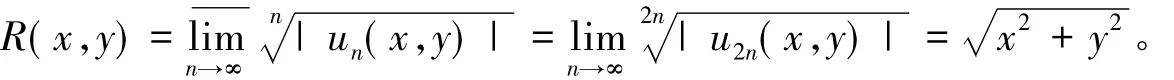
例3 求二元幂级数

的收敛半径及收敛域。
解 由于原级数可写为

这是z=x2y3的一元幂级数,其收敛半径为所以,当时,原级数绝对收敛;当时,原级数发散;当时,有,可见,原级数的通项不趋近于0,从而发散。因此,原级数的收敛域为



图2
解 因为

为z=x+y2的幂级数,其收敛半径为1,收敛域为[-1,1],从而原级数的收敛域为

进一步,由一元函数的泰勒展开式知,原级数的和函数为arctan(x+y2),即

现在考虑该二元幂级数的收敛半径。首先,画出|x+y2|=1的图像(见图3)。收敛域就是两条曲线y2=-(x-1)(x≤1)和y2=-(x+1)(x≤-1)围成的无界闭域。设在曲线y2=-(x-1)(x≤1)上任意一点(x,y)到原点的距离为d,则它在处取得最小值由于曲线y2=-(x+1) (x≤-1)上任意一点(x,y)到原点的距离大于等于所以该二元幂级数的收敛半径如图3所示。

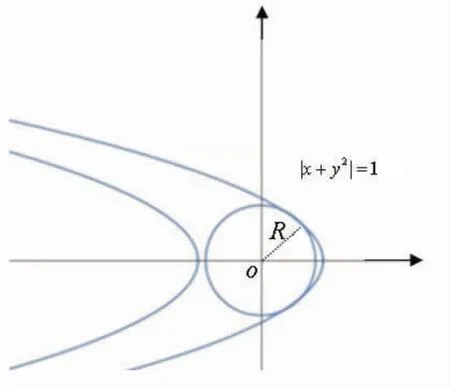
图3 |x+y2|=1的图像及其收敛半径,收敛域为两条抛物线之间的无界闭域
[1]华东师大数学系.数学分析(下册)[M].北京:高等教育出版社,2010:142-145.
[2]曹飞龙,徐宗本,梁吉业.多项式函数的神经网络逼近:网络的构造与逼近算法[J].计算机学报,2003,26(8):906-912.
[3]王建军,徐宗本.多元多项式函数的三层前向神经网络逼近方法[J].计算机学报,2009,32(12):2482-2488.
[4]高潮邦.关于多元幂级数[J].大学数学,2007,23(3):125-129.
[5]蔡道西.关于二元幂级数收敛半径的计算公式[J].数学学习与研究(教研版),2009(5):111-112.
[6]周焕芹.一个关于 SP(n)的无穷级数的收敛性[J].渭南师范学院学报,2011,26(12):5-7.
[7]王永兴,杨倩丽.关于幂级数在自然数列中的应用[J].渭南师范学院学报,2005,20(5):21-23.
