基于求幂级数和函数的方法研究

熊允发

(中国人民公安大学信息技术与网络安全学院， 北京 100038)

0 引言

在微积分课程中，幂级数是重要的组成部分。它结构最简单、应用最广泛。在公安应用统计中，可计算随机变量的数学期望、方差、数字特征等，在金融领域，计算相应的利率金额，在工程计算中，更可用于较复杂的函数化简。

为了实现幂级数的应用探索，必须要掌握幂级数和函数的求解问题。这是解决幂级数问题的核心，只有熟练掌握幂级数的和函数，才有可能进行反向的探索和拆分精简。什么是幂级数和函数？它的收敛域为何？如何来求和函数呢？正是本文探讨的重点。首先从和函数的界定以及求和函数的各种方法入手。

1 幂级数和函数的概念界定

1.1 幂级数和函数的定义[1]

具有下列形式的函数项级数

称为在点x0处的幂级数。

称为在点0处的幂级数。

若对幂级数中的每一个x，都有a0+a1x+a2x2+a3x3+…=s(x)，则称s(x)为幂级数的和函数。

简言之，幂级数的和函数即是无穷个幂函数之和。因此使得幂级数有和函数的自变量x的取值范围，称之为幂级数的收敛域或收敛区间。而收敛区间的一半简称为收敛半径R。

1.2 幂级数和函数的性质[2]

由1.1可知，我们可以把幂级数的部分和记为

sn(x)=a0+a1x+a2x2+a3x3+…+anxn

且部分和sn(x)的极限就是和函数。即

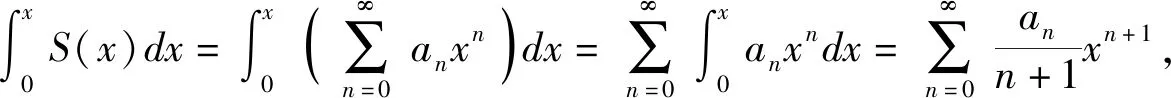
2 求幂级数和函数的方法探究

2.1 定义法[3]

解：当|x|<1时

2.2 逐项求导法

若幂级数通项的系数是自然数的倒数或相邻的自然数乘积的倒数，即n在分母上时，可考虑用“先求导，再积分”的做法。

解：由题意，易知幂级数的收敛区间为[-1,1]

当x≠0时 不妨设

先上式两边求导得：

再求导得：

这样经过两次求导得出了一个系数不含n的幂级数，利用无穷递缩等比数列的求和公式就能得出

上式两边积分得：

再积分得：

于是就得到当x≠0时的和函数为

综上所述

2.3 逐项积分法[4]

若幂级数通项的系数是自然数或相邻的自然数相乘的形式，即n在分子上时，一般可考虑用“先积分，再求导”的做法。

解：由题意，易知幂级数的收敛域为(-1,+1)。

设

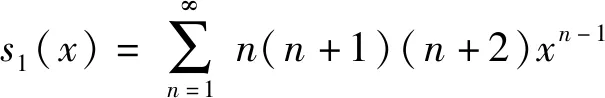
先上式两边积分得：

再积分得：

再积分得：

这样经过三次积分后就得出了一个通项不含n的幂级数了，于是我们利用无穷递缩等比数列的求和公式求出

对上式第一次求导得：

第二次求导得：

第三次求导得：

从而可得所求和函数

2.4 其他方法

易知x=-1时级数收敛，x=1时级数发散，所以该幂级数的收敛域是[-1,1)

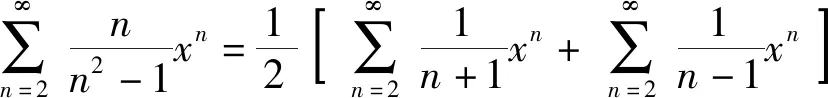
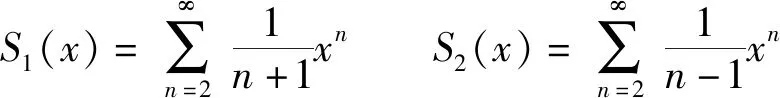
不难求出:

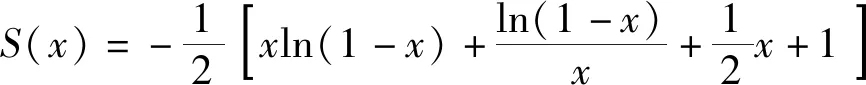
S(x)=0

故有

解：由题意，易见该幂级数的收敛域为(-∞,+∞)

(1)

对(1)的两端两次求导分别得

(2)

(3)

∴S(x)=(x+x2)exx∈(-∞,+∞)

3 总结