结构可靠度分析的一种改进蚁群算法

2015-02-23白海霞荆州市路远市政工程有限公司湖北荆州434000

长江大学学报(自科版) 2015年28期

白海霞　(荆州市路远市政工程有限公司，湖北荆州 434000)

结构可靠度分析的一种改进蚁群算法

白海霞(荆州市路远市政工程有限公司，湖北荆州 434000)

[摘要]基本蚁群算法存在过早收敛、容易陷入局部最优解等问题。引入信息熵H,通过控制信息熵的值来改进参数τ,从而对基本蚁群算法进行改进,并使用改进后的蚁群算法来求解可靠指标,对结构体系进行更为准确的结构可靠度研究,以提高结构可靠度的计算效率与计算精度。将改进的蚁群算法应用于10杆桁架结构,应用结果证明该研究方法具有很强的适用性和有效性,为研究大型复杂结构的可靠性问题提供了一种新的方法。

[关键词]结构可靠度;计算智能;蚁群算法

可靠度的研究早在20 世纪30年代就已经开始，当时主要是围绕飞机失效进行研究，可靠度在结构设计中的应用始于20世纪40年代。结构可靠度的计算是结构设计中的核心内容，近20年来取得了很大的进展，已经提出了许多近似计算方法[1~5]。工程中常用的可靠指标计算方法主要有一次二阶矩法、JC法、梯度优化法以及响应面法、蒙特卡罗法及随机有限元等[6，7]。使用这些方法常会遇到很多复杂问题难以解决，如极限状态曲面难以解析描述，仿真计算量大，难以做到有效搜索解空间来找到标准正态空间原点至极限状态曲面的最短距离[8]以及最短失效路径[9]等问题。近些年来，计算群体智能算法[10]迅猛发展，其中蚁群算法(Ant Colony Optimization，ACO)可用在系统设计、多目标优化、模式识别、信号处理、决策制定、工件排序、车辆调度和建设工程等领域[11~17]。为此，笔者提出了一种结构可靠度分析的改进蚁群算法。

1结构可靠度计算模型

结构可靠度是结构设计中不可或缺的重要内容，结构可靠度是指结构在规定时间内、规定条件下，完成预定功能的概率，是人们在工程实践中逐渐对荷载和材料的不确定因素认识的基础上发展起来的。结构可靠度理论是为了解决工程结构设计、施工和使用中存在的不确定性问题，它在结构分析和设计中起着非常重要的作用。结构可靠度的分析是建立在结构可靠与不可靠的界限状态，即极限状态(Z=R-S，R为结构的抗力，S为结构的作用效应，当Z>0时结构处于可靠状态，Z<0结构处于失效状态，Z=0，结构处于极限状态)。可靠指标和失效概率一样都可以衡量结构的可靠度，所以常常通过计算可靠指标来分析结构可靠度。

在结构可靠度分析中，结构可靠指标β的几何意义是标准正态空间内，坐标原点到极限状态曲面的最短距离。

假设x1,x2,…,xn是结构中的随机变量，由这些随机变量组成的极限状态方程为：

z=g(x1,x2,…,xn)=0

把β看成极限状态曲面上点p(x1,x2,…,xn)的函数，通过优化求解，找到β最小值。约束优化模型如下：

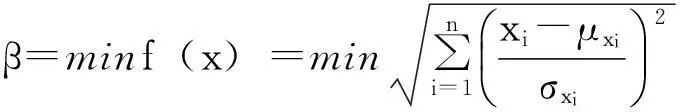
(1)

式中， μxi、σxi分别为随机变量xi的均值和标准差。

采用罚函数法将式(4)变成相应的无约束优化问题：

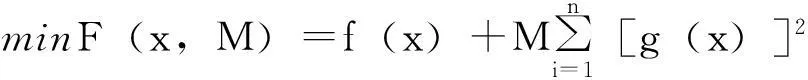
(2)

式中，M为相应的罚因子(足够大的正数)，相应的项为罚项。

2改进的蚁群算法

蚁群算法[18]是由意大利学者Dorigo于1992年首次提出的一种优化算法，经过大量研究发现，蚂蚁个体之间是通过一种被称为信息素的物质进行信息传递的。蚂蚁在运动过程中，能够在它所经过的路径上留下这种物质，而且能够感知该物质的存在，并以此指导自己的运动方向。蚁群算法不涉及到目标函数的偏导数计算，且能够克服其他算法容易陷入局部最优的缺点，因而具有较强的适应性。目前，蚁群优化算法已成功地应用于包括函数优化、水利工程和边坡工程等在内的诸多领域。

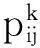
(3)

信息素的更新公式为：

τij(t+1)=ρ·τij(t)+Δτij

(4)

(5)

为了解决基本蚁群算法的过早收敛问题，采用文献[19]的方法，即引入信息熵H，通过控制信息熵的值来改进参数τ，进而对蚁群算法进行改进。开始时每条路径都会有等量的信息素，信息熵取最大值，随着信息素的增加，信息熵值逐渐变小，继续进行容易出现早熟以使算法出现停滞现象，所以此时通过控制与信息熵有关的α(t)和β(t)的值来控制此时最优路径出现的区域和信息素更新的范围，进而避免了早熟和停滞现象的发生。

改进后的蚁群算法步骤如下：

1)初始化参数，τij(0)=0;

2)将m只蚂蚁放在n个结构单元上;

3)按公式(1)计算每只蚂蚁移动到下一个结构单元的概率;

4)m只蚂蚁遍历n个结构单元后，路径上的信息素增加;

5)所有路径信息素按式(2)、(3)更新，进行局部寻优;

6)多次重复3)～5)步，进行全局寻优，找出最优解。

3实例分析

10杆桁架结构如图1 所示，各杆的横截面积Ai为正态分布的基本变量，均值为6.452×10-3m2，变异系数为0.05，杨氏模量为6.895×1010Pa，施加荷载为p1=p2=4.45×105N，结构极限状态取为桁架的最大位移不超过0.1016m，求此时结构的可靠度。

采用改进后的蚂蚁算法对可靠指标进行求解，算法的迭代收敛过程如图2所示。

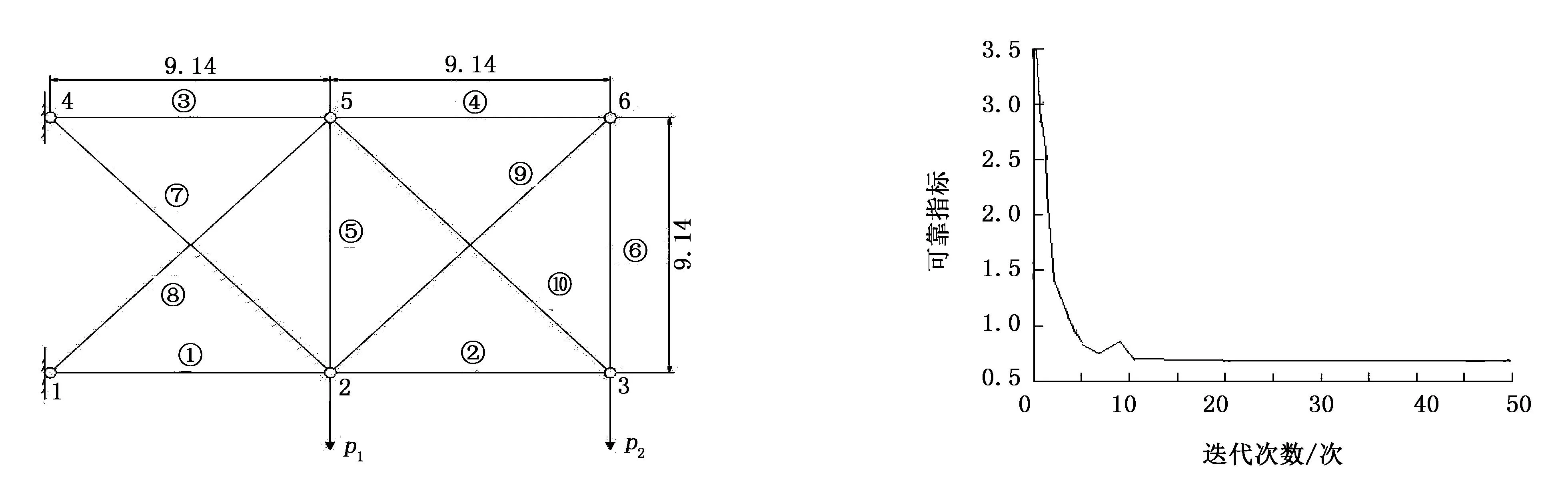
图1　10杆桁架示意图　　　　　　　　　　　　　　　　　　　　　　　图2　迭代过程

从图2可以看出，在第10次迭代时就已经收敛并达到最好的精度。随着进一步迭代，算法收敛到最优值。与传统方法[20，21]的迭代过程相比，改进的蚂蚁算法能达到较好的计算精度，具有良好的适用性(见表1)。

表1　计算结果比较

4结语

结构可靠度理论是结构设计和规范制定的基础，在某种程度上标志着一个国家结构工程发展的水平。而智能算法是近年来出现的解决复杂工程的高效方法，相比传统优化方法智能算法具有运算速度快、求解精度高等优点。为提高结构可靠度的计算效率，笔者通过一种改进的蚁群算法计算结构的可靠指标，对结构体系进行了更为准确的结构可靠度研究，该分析方法为研究复杂结构的可靠性问题提供了一种新的思路。

[参考文献]

[1]Moses F.System reliability developments in structural engineering[J].Structural Safety，1982，1(1):3～13.

[2] 张明.结构可靠度分析——方法与程序[M].北京：科学出版社，2009.

[3] 谭海涛，徐定海，王善.一种计算结构可靠度的一元分解法[J].哈尔滨工程大学学报，2009，30(8):883～886.

[4] 张建仁，许福友.计算结构可靠指标的子域抽样法[J].土木工程学报，2003，36(12):39～43.

[5] 周彬彬，顾祥林，张伟平，等. 海洋大气环境下钢筋混凝土梁受弯时变可靠度分析[J].土木工程学报，2010，43(S2):15～21.

[6] 吕大刚，贾明明，李刚.结构可靠度分析的均匀设计响应面法[J].工程力学，2011，28(7):109～116.

[7] 武清玺. 结构可靠性分析及随机有限元法[M].北京: 机械工业出版社，2005.

[8] 阎宏生，胡云昌，李向京.结构可靠性分析的一种新方法[J].天津大学学报，2000，33(6):32～35.

[9] 蔡文学，程耿东. 灾害荷载下弹塑性结构体系可靠度的近似计算[J].大连理工大学学报，1996，36(1):6～12.

[10] 梁艳春，吴春国，时小虎，等.群智能优化算法理论与应用[M].北京：科学出版社，2009：75～132.

[11]Liu Qiang， Wang Chengen. A discrete particles swarm optimization algorithm for rectilinear branch pipe routing[J]. Assembly Automation，2011，31(4):363～368.

[12]Liens I D， Moure M D C， Zio E， et al.A particle swarm-optimized support vector machine for reliabilityprediction[J]. Quality and Reliability Engineering International，2011，6(3)1221～1230.

[13]Mousa F M.Particle Swarm Optimization Algorithm for Smart Antenna System[J]. Journal of Mobile Communication， 2011， 5(1):6～10.

[14] 王正武，罗大庸，黄中祥，等.线控系统协调优化模型及其改进粒子群算法研究[J].系统工程理论与实践，2007(10):165～171.

[15] Zhu Yonghua，Xu Jin，Ye Wentong， et al.The Advanced Ant Colony Algorithm and its Application. Measuring Technology and Mechatronics Automation (ICMTMA)[A].2011 Third International Conference[C].2001:664～667.

[16] Wang Yunlong， Kueiming L.Generic Cabling of Intelligent Buildings Based on Ant Colony Algorithm. International[J]. Journal of Software Science and Computational Intelligence (IJSSCI)， 2011，3(2):49～61.

[17] Ghafurian S， Dian N J.An ant colony algorithm for solving fixed destination mult-depot multiple traveling salesmen prolem[J]. Journal Applied Soft Computing，2011，11(1):10～16.

[18] Shi X H， Wang L P， Zhou Y，et al. An ant colony optimization. Method for prize collecting traveling salesman problem with time windows[A].Proceedings of the 4th International Conference on Natural Compution (ICNC 2008)[C].2008，7:480～484.

[19] Li Yancang，Li Wanqing. Adaptive Ant Colony Optimization Algorithm Based on Information Entropy: Foundation and Application[J]. Fundam Inform，2007，77(3): 229~242.

[20] 张银龙，常大民.响应面法用于桁架体系可靠度分析[J]. 工程设计CAD与智能建筑，2002(11)：57～60.

[21] 魏锦辉，董笑慧，魏保立.遗传算法及其在结构可靠度计算中的应用[J].河南科学，2009，27(10):1261～1263.

[编辑]计飞翔