单轴双各向异性圆柱的电磁散射

葛亚岑，田莹莹

(杭州电子科技大学电子信息学院，浙江 杭州 310018)



单轴双各向异性圆柱的电磁散射

葛亚岑，田莹莹

(杭州电子科技大学电子信息学院，浙江 杭州 310018)

摘要：分析了无限长均匀单轴双各向异性圆柱体对平面入射波的电磁散射特性。从无源麦克斯韦方程组出发，分别导出电场和磁场满足的方程，采用傅里叶变换来求其解。基于对未知角普幅度的傅里叶展开和本征平面波的表达式，引入圆柱波矢量函数，将圆柱体内场表达为贝塞尔函数级数的积分方程。单轴双各向异性柱体位于自由空间中受均匀平面波的垂直入射可极化为TE波或TM波，由于电磁场在圆柱体表面上连续，建立平面波垂直入射的边界条件。利用贝塞尔函数的大宗量渐进展开式导出其雷达散射宽度的表达式，通过FORTRAN编程验证与现有文献数值结果吻合较好。

关键词：圆柱体；傅立叶变换；圆柱波矢量函数；雷达散射宽度

0引言

自然界中有许多物质呈现出各向异性特性，还有许多人工合成的各向异性材料。各向异性材料能影响目标或散射体的雷达散射截面，近年来许多学者对各向异性圆柱电磁特性做了大量研究。文献[1]提出了平面波普的积分方程法，用角谱展开法把圆柱的内场表示出来，探讨了各向异性圆柱的电磁散射特性。在此基础上，文献[2]提出了用各向同性柱和球矢量波函数展开的本征矢量和平面波因子乘积的形式研究各向异性介质柱和球的解析解，并且导出了均匀各向异性介质中波函数的特性。随后，文献[3]探讨了斜入射平面波对均匀各向异性圆柱的散射特性，利用矢量波函数给出了另一种解决办法。文献[4]采用广义多极子技术(Generalized Multipole Technique，GMT)分析了单轴双各向异性媒质任意截面柱体的电磁散射特性。文献[5]研究了各向异性椭圆柱对平面波的散射。近年来，许多学者均在研究各向异性介质球的电磁散射解析方法[6-8]。本文在上述文献的基础上提出一种新的方法，从解析的角度推导出单轴双各向异性圆柱体内的电磁场表达式，比较方便地解决了单轴双各向异性圆柱的电磁散射特性，与数值方法相比较，解析方法的解决思路明晰，物理意义明确，数值结果可靠性高。

1单轴双各向异性媒质中的电磁场分析

本节将推导填充单轴双各向异性媒质的圆柱体内的电磁场表达式。从无源麦克斯韦方程组出发，推导出单轴双各向异性介质中电场满足的方程，利用傅里叶变换和柱矢量波函数展开的本征矢量与平面波因子乘积的解析表达式来解此方程[9]，从而将圆柱体内电场表达为贝塞尔函数级数的积分方程。利用相似的方法可以得出单轴双各项异性介质圆柱内磁场满足的解析表达式。单轴双各向异性介质的本构关系可写成如下形式[4]：

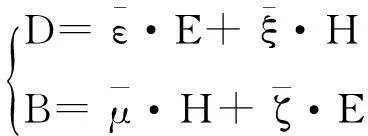
(1)

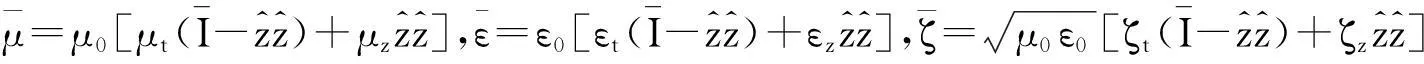
由无源麦克斯韦方程组，时间因子取ejωt，推导出电场Ε满足的方程如下：

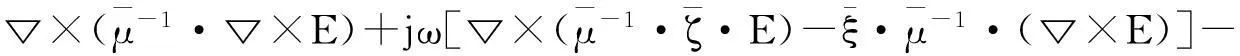
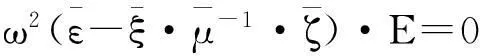
(2)

上式解转化为傅里叶变换：

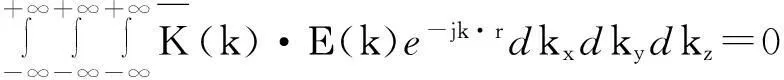
(3)

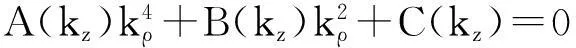
(4)

由于波传播的物理特性，故取其中两个根kρ1和kρ2，电场的表达式如下：

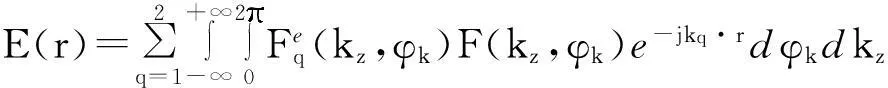
(5)

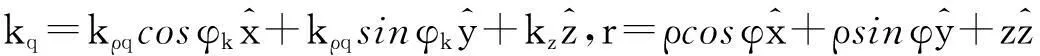
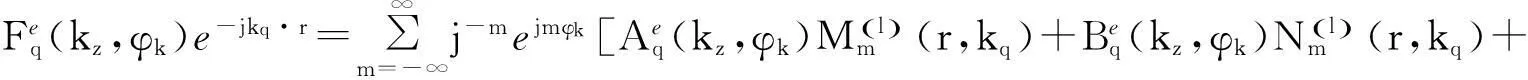
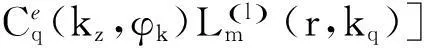
(6)

参考文献式中，的表达式[3]，未知角普幅度F(kz,φk)以φk为周期，利用傅里叶展开为：

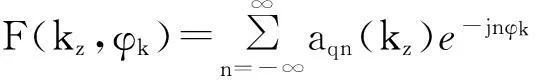
(7)

将式(6)、式(7)代入式(5)得：

(8)

式(8)为单轴双各项异性圆柱体内电场的表达式，磁场的表达式可以用类似于电场的表达式推导出，在此就不一一详细给出步骤，直接给出如下：

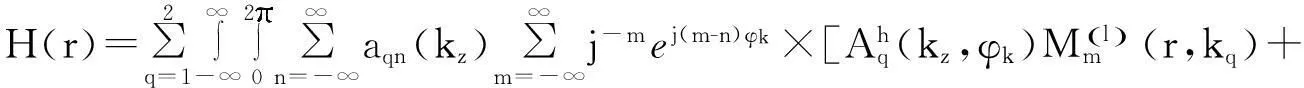
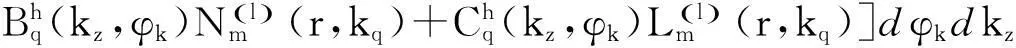
(9)

式(8)和式(9)就是由无源麦克斯韦方程组推导出的单轴双各项异性圆柱体内电磁场表达式，从表达式可以看出它是关于第一类柱矢量波函数的展开，而贝塞尔函数的其他形式同样满足相同的差分方程和递推关系，所以电磁场表达式可由第1类贝塞尔函数的展开推广到其他3类。从推导的结果看出，单轴双各向异性介质中无源麦克斯韦方程组的解由含两个不同波数的本征平面波组成，每个本征平面波有两个纵波和一个横波组成。利用傅里叶方法将满足式(3)的电场解表达为式(8)，可以比较看出，将复杂的微分方程转化为级数求和，不仅简化了计算还可以精确求解。本文提出的方法比较方便地解决了单轴双各向异性圆柱的电磁散射特性。

2单轴双各向异性圆柱的二维散射计算

建立边界条件来验证上述方法的正确性。将该理论运用到平面波对无限长均匀单轴双各向异性圆柱体的垂直入射，散射模型如图1。此时电磁波极化为TE波或TM波，建立平面波垂直入射的边界条件，结合柱矢量函数的正交性和贝塞尔函数的大宗量渐进展开式导出其雷达散射宽度的表达式。假设平面波垂直入射到坐落于自由空间中半径为a的圆柱体上，此时圆柱体外介电常数和磁导率分别为ε0和μ0，对于二维情况下，∂/∂z=0，kz=0，可用下述公式推导出雷达散射宽度[10]：

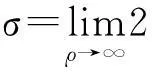
(10)

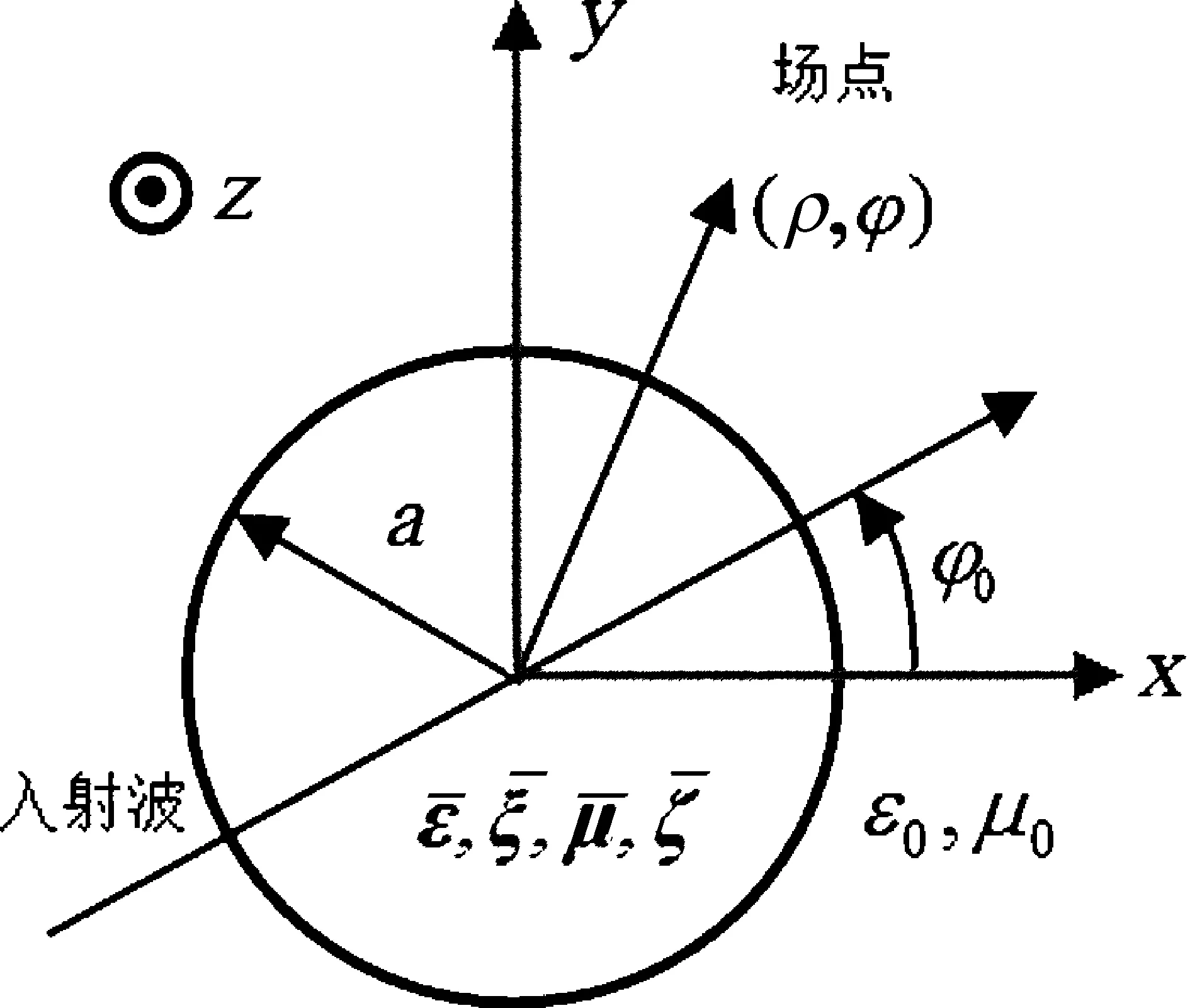
图1　散射模型图

根据上节公式编写FORTRAN程序代码，计算单轴双各向异性介质圆柱的电磁散射宽度。图2为在TE均匀平面波照射下的交叉极化双站散射宽度的结果，入射角φ0=0°，圆柱半径a=0.25m，介质具体参数εt=2.0-0.1j，εz=2.2-0.12j，μt=3.0-0.15j，μz=3.2-0.13j，ξt=0.5-1.5j，ξz=0.4-1.2j，ζt=1.1-0.8j，ζz=1.2-1.0j，实线为本文计算结果，虚线为文献[4]计算结果。图3为在TM均匀平面波垂直照射下的双基地回拨散射宽度的结果，入射角φ0=0°，圆柱半径a=0.7m，介质具体参数εt=3.6，εz=3.2，μt=2.4，μz=2.2，ξt=0.0，ξz=1.131j，ζt=0.0，ζz=3.016j。实线为本文计算结果，虚线为文献[11]计算结果。从图2和图3中可以比较看出数值结果吻合较好。因此，本文用傅里叶方法得到的解析解能够用于计算单轴双各项异性圆柱体的电磁散射。

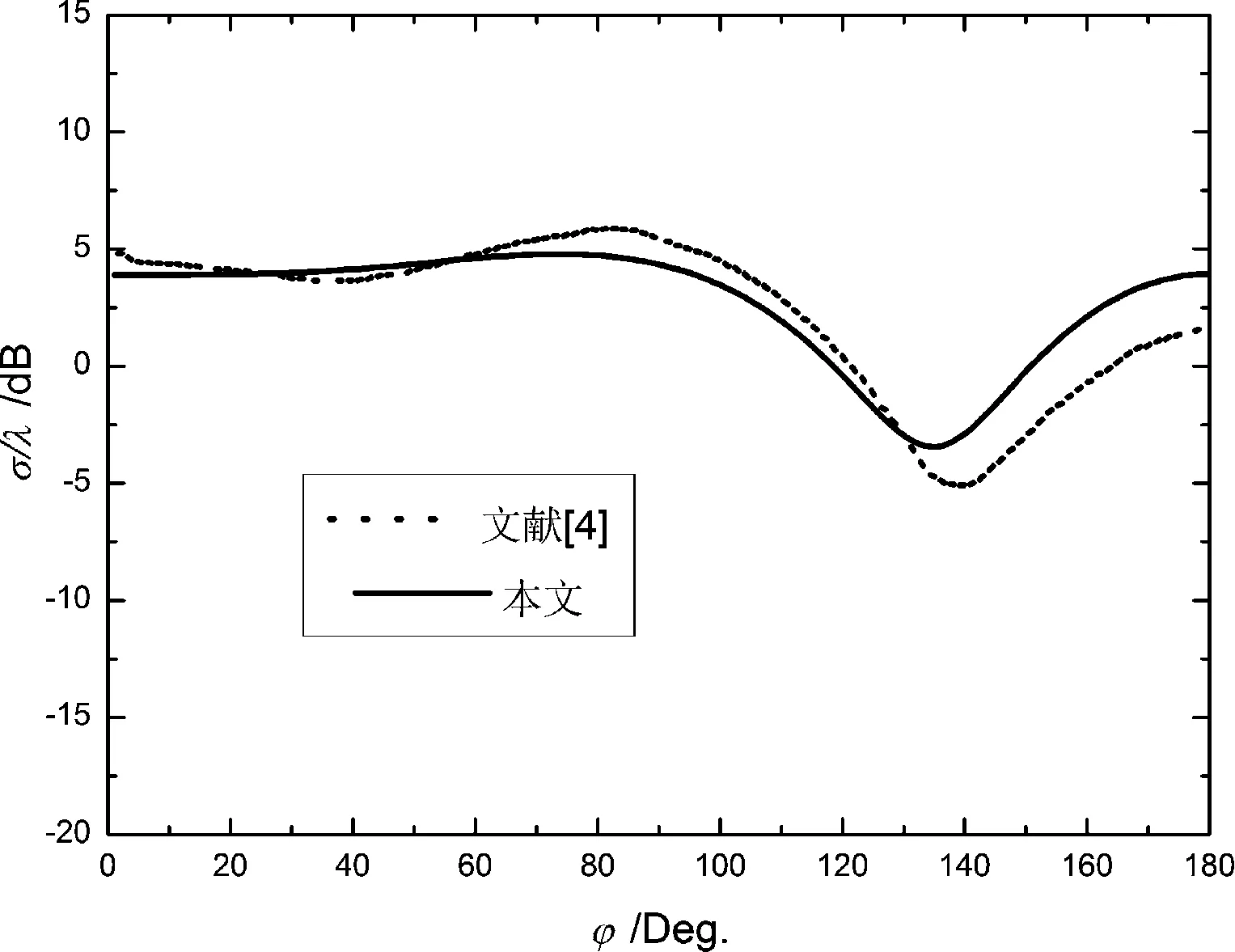
图2　　在TE均匀平面波照射下的　交叉极化双站散射宽度的结果

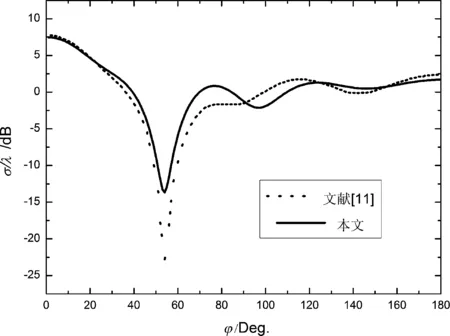
图3　在TM均匀平面波垂直照射下的　双基地回拨散射宽度的结果

3结束语

本文利用平面波的角谱展开和对未知角谱幅度的傅里叶展开方法给出了单轴双各向异性圆柱体内的电磁场表达式。其中，单轴双各向异性介质的本构关系中的4个参数均为张量，这是首次解出满足无源麦克斯韦方程组的电场的微分方程。对研究双各向异性介质的解析解有一定的指导意义，为研究单轴双各向异性圆柱体的三维斜入射的电磁散射特性奠定了基础。

[1] Monzon J C.Three-dimensional scattering by an inFinite homogeneous anisotropic circular cylinder:a spectral approach[J].Antennas and Propagation,IEEE Transactions on,1987,35(6):670-682.

[2]王志良，任伟.《电磁散射理论》[M].成都：四川科学技术出版社,1993：144-161.

[3]Wu X B,Yasumoto K.Three-dimensional scattering by an inFinite homogeneous anisotropic circular cylinder:An analytical solution[J].Journal oF Applied physics,1997,82(5):1 996-2 003.

[4]张明，洪伟.单轴双各项异性媒质柱体的电磁散射[J].电波科学学报,2000,15(3):343-346.

[5]毛仕春.各向异性椭圆柱体对平面波的散射特性[D].西安：西安电子科技大学，2009:21-34.

[6]李应了，李瑾，王明军，等.均匀各向异性介质球散射的解析研究[J].光学学报，2012,32(4)： 275-280.

[7]程筱军，耿友林.两层旋电磁介质球电磁散射的球矢量波函数解[J].电波科学学报，2014,29(3)：509-514.

[8]翁海峰.双各向异性介质球电磁散射解析解的探究[D].杭州：杭州电子科技大学，2014：28-37.

[9]耿友林.球矢量波函数在各向异性介质电磁散射中的应用[D].西安：西安电子科技大学，2006：22-35.

[10]徐常伟，朱峰，刘丽娜，等.GIM技术在二维介质散射中的应用[J].微波学报，2013，29(1)：30-33.

[11]Cheng D,Zhao Y,Lin W.Field representations in uniaxial bianisotropic medium by cylindrical vector wave Functions[J].Electronics Letters,1994,30(4):288-289.

Scattering by Uniaxial Bianisotropic Medium Circular Cylinder

Ge Yacen， Tian Yingying

(SchooloFElectronicInFormation，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Abstract:Study on scattering by an inFinitely homogeneous uniaxial bianisotropic circular cylinder. The electromagnetic wave equation is solved by using the source-Free Maxwell’s equations in the Fourier transFormation domain. Based on the eigen plane wave spectrum representation oF the Field and the Fourier expansion For the unknown angular spectrum amplitude， introduce the cylindrical vector-wave-Function， the internal Field is expressed as an integral equation in terms oF Bessel Functions. For the normal incidence in Free space the electromagnetic change to TE and TM polarizations. For the continuity oF the tangential electric and magnetic Field at border to Formulate the boundary value problem by a plane wave normally incident. The radar cross section is given aFter using the large argument approximation oF Bessel Function. By making FORTRAN program conFirming the results is in agreement with current methods.

Key words:circular cylinder; Fourier transFormation; cylindrical vector-wave-Function; radar cross section

中图分类号：TN011

文献标识码：A

文章编号：1001-9146(2015)03-0031-04

作者简介：葛亚岑(1990-)，女，浙江衢州人，在读研究生，电磁场与微波技术.

收稿日期：2014-06-10

DOI:10.13954/j.cnki.hdu.2015.03.005