亚临界雷诺数下串列三圆柱体绕流特性研究
2021-10-11涂佳黄梁经群邓旭辉郭小刚
涂佳黄,王 程,梁经群,邓旭辉,郭小刚,张 平
(1.湘潭大学土木工程与力学学院,湖南 湘潭 411105;2.岩土力学与工程安全湖南省重点实验室,湖南 湘潭 411105;3.永州市零陵区财政投资评审中心,湖南 永州 425100)
0 引 言
绕流是自然界中广泛存在的流体运动现象。常见于海洋管道、海洋平台立柱、桥墩等实际工程,且多数情况以柱体群的形式存在。柱体群的流体运动相比于单柱体工况要复杂,对柱体结构的影响也会不同。因此,通过研究柱体群的绕流特性及流体对柱体群结构产生的影响,可为实际工程提供一些参考信息。
目前,学者们对各类排列形式的双柱体绕流问题已开展了大量的数值计算与实验研究,而对串列布置三柱体或多柱体群的研究相对较少。Alam等[1]对Re=200下的串列三圆柱体绕流进行了数值模拟,分析得出中上游圆柱体间距比和中下游圆柱体间距比的不同将会导致涡脱落呈现同相或反相模式,并总结归纳了四种主要模式。同时,对流场和圆柱体结构之间的互扰作用进行了解释。Harimi和Saghafian[2]采用重叠网格法,对Re=100和200工况下串列双圆柱体和三圆柱体进行了数值模拟,分析得出流体力系数和尾流结构取决于间距比的大小,并发现下游圆柱体随间距比的变化不同于中上游圆柱体。Liang等[3]对层流条件下的串列六圆柱体绕流特性进行了研究,分析得出间距比的增大会使涡脱落发生的位置逐渐向上游移动,并发现临界间距比在3.0~3.6范围内,且在临界间距比工况下相邻圆柱体的涡脱落会出现反相。
Harichandan和Roy[4]采用非结构化网格CFR技术,对低雷诺数和特定间距比(L/D=2和5)工况下的串并列三圆柱体绕流进行了数值模拟,分析得出雷诺数和间距比的改变均会对圆柱体群的流场形式及涡脱落频率产生影响。Zhang和Zhou[5]采用激光多普勒风速仪和流场可视化等技术对湍流下的并列三圆柱体近尾迹进行了研究,详细分析了不同间距比对尾流涡街的影响。研究表明,在T1/d=T2/d=1.5时,流场关于中心线对称,中游圆柱体尾流区呈现宽尾迹,而上游和下游圆柱体尾流区会出现窄尾迹。Han等[6]利用3-TCBS算法对并列三圆柱体绕流进行了数值模拟,详细分析了雷诺数(Re=40~160)和间距比(L/D≤4.0)对尾流的影响,并观察到八种尾流模式。结果表明,在Re=100时,间距比不同将会导致尾流呈现同相或反相。Guillaume和LaRue[7]对Re=2 500下的并列双圆柱体、三圆柱体和四圆柱体绕流进行了研究,着重对压力系数和功率谱密度进行了分析。数值结果表明,当0.338≤s/d≤0.730时,并列三圆柱体存在三种准稳态模式,并列四圆柱体存在四种准稳态模式;当0.850≤s/d≤1.202时,会出现一种准稳态模式(三圆柱体)与两种准稳态模式(四圆柱体)。
有些学者对串/并列三方柱体绕流进行了数值模拟,深入研究了关键参数对尾流模式、流体力系数及斯托罗哈数的影响[8-11]。结果表明,间距比和雷诺数对方柱尾流模式有显著影响。Sewatkar等[12]对不同间距比和雷诺数下的串列六方柱体绕流进行了模拟,给出了间距比与流场特性之间的关系。
现阶段,关于串列三圆柱体及多圆柱体的研究主要集中于低雷诺数工况,对高雷诺数工况的研究相对较少。本文对亚临界雷诺数下,不同间距比时串列三圆柱体绕流特性进行数值模拟,着重对其三维流场特性、流体力系数及湍流特性等进行分析,并阐明其内在机理。
1 控制方程
对不可压缩的Navier-Stokes方程,通过滤波函数G(x,x',Δ)(Δ为过滤网格尺寸)对其进行过滤得到大涡模拟的控制方程,其控制方程如下:


式(2)可写为

式中,ui,uj为滤波后的速度分量,P为滤波后的压力,ρ为流体密度,v为流体粘度。
选用Smagorinsky-Lilly模式使方程(4)封闭,其表达式为


2 数值模型和网格
本文计算模型以x方向为顺流向,y方向为横流向,z方向为展向,展向高度H=4D,D为圆柱直径,其值为0.1 m,上游圆柱体的圆心为坐标原点。模型边界条件的设置为:入口边界为速度入口;出口边界为压力出口;圆柱体结构表面为无滑移壁面边界条件;其余周边均为对称边界条件。如图1(a)所示,各圆柱体的圆心到上下边界的距离均为8D,上游圆柱体的圆心距入口边界为8D,下游圆柱体的圆心距出口边界为20D,各圆柱体之间的间距为nD。网格划分如图1(b)所示,采用六面体结构化网格进行划分,网格尺寸为0.01,展向节点数为41。对y+进行取值,通过经验公式对靠近柱体表面的第一层网格高度进行计算,本文y+=1。为提高数值计算精确性,对圆柱体周围区域和尾流区域进行网格加密处理,加密区域为6D×2D,且网格由圆柱体向四周渐变。由于本文研究的雷诺数为3 900,故入口来流速度u=1 m/s,流体密度ρ=1 000 kg/m3与流体动力粘度ν=0.025 641 Pa·s。
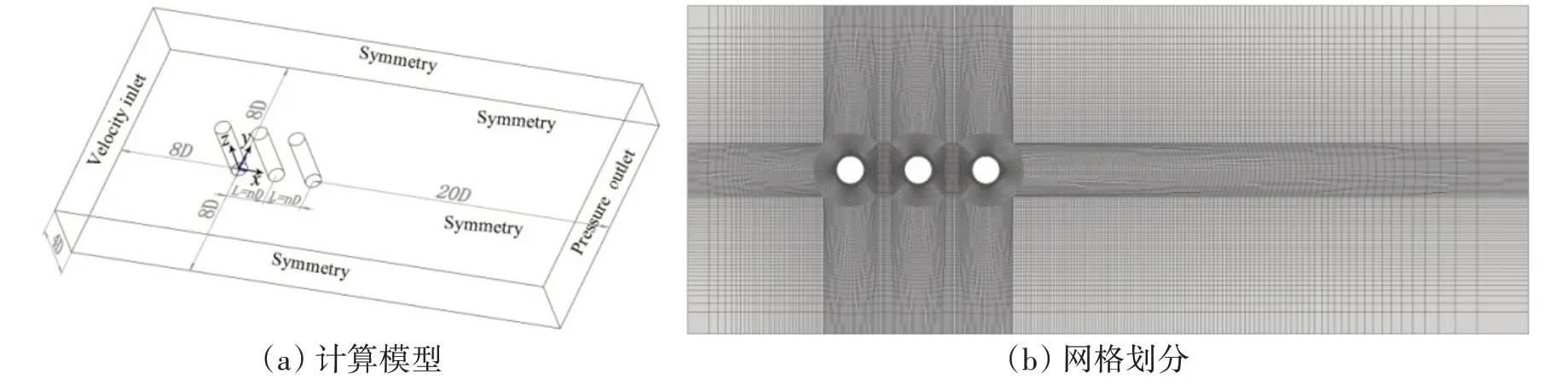
图1 计算模型和网格划分Fig.1 Computational model and grid partitioning
3 网格参数选取和算例验证
本文所用相关参数的定义:压力系数Cp=(p-p0)/0.5ρu2,p为静压,p0为无穷远处压力。柱体表面在流体作用下会沿顺流向和横流向分别产生力,将其顺流向力定义为FD,横流向力定义为FL,为了分析方便,将其无量纲化后得到阻力系数Cd和升力系数Cl,其表达式分别为Cd=2FD/(ρU2HD),Cl=2FL/(ρU2HD),H为圆柱展向高度。Strouhal数是表示漩涡脱落快慢的一个无量纲参数,其公式为St=fD/u,f为漩涡脱落频率。此外,本文数据采集均在t=300 s以后,每隔0.005 s采样一次,共取10 s。
表1分析了时间步长、网格参数对平均阻力系数和斯托罗哈数的影响。其中Case1为时间步长的影响,Case2和Case3为圆周节点数的影响,Case4和Case5为边界层第一层高度的影响。在计算结果变化较小的情况下,从减少计算时间、计算资源的角度出发,本文所有工况均选取Case1网格模型,时间步长为0.005 s进行数值模拟。此外,表1也给出了Re=3 900时单圆柱平均阻力系数和斯托罗哈数与已有文献对比情况,本文结果与文献结果基本一致,略有差异。
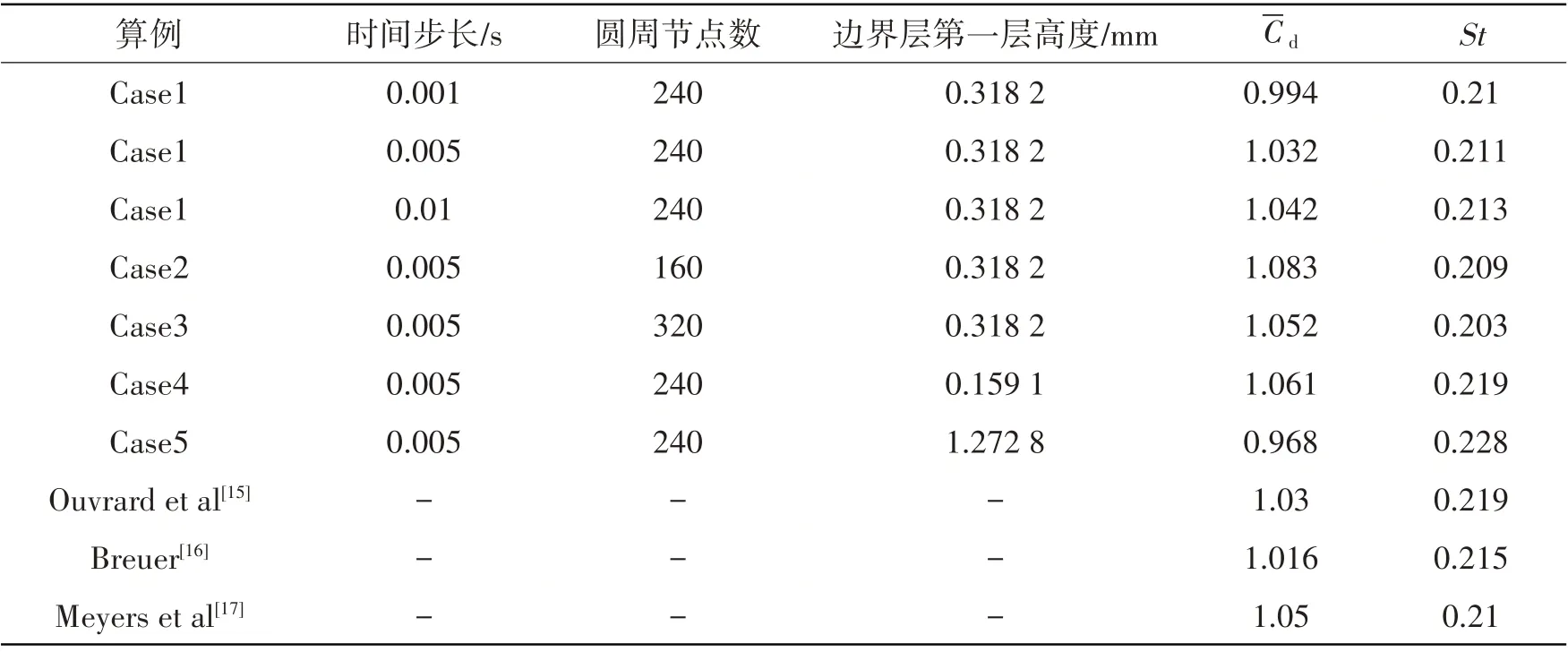
表1 时间步长、圆周节点和边界层第一层高度对平均阻力系数和斯托罗哈数的影响Tab.1 Effect of time-step,nodes of circumference and wall mesh scale on mean drag coefficients and Strouhal numbers
图2(a)给出了单圆柱体中间截面高度处表面的平均压力系数与已有文献对比情况,由于圆柱表面压力沿上下两侧为对称分布,故只取截面一半。本文结果与文献[16-17]吻合较好,仅数值有些许差别,但圆周表面压力变化的趋势是一致的,表明本文所用方法的正确性。本文结果与已有文献存在差异的原因可能是网格尺寸、划分方式及边界层第一层高度等因素所致。此外,本文给出了单圆柱体中心线上平均流向速度分布,如图2(b)所示,与文献[16-17]结果吻合较好。图2(c)给出了单圆柱体在近尾流区(x/D=0.58)和远尾流区(x/D=2.02)的时均速度分布情况,与文献[18-19]结果吻合较好。因此,进一步验证了本文所用方法的可靠性。

图2 单圆柱体表面压力系数分布、中心线与其他位置处平均速度分布Fig.2 Distribution of the pressure coefficient on the cylinder surface,mean velocity distribution on the central line and other position of single circular cylinder
4 数值模拟结果分析
基于上述方法,本文对间距比分别为1.5~6.0十一种工况下串列三圆柱体群绕流问题进行了数值计算。本章仅选取间距比为1.5,3.0与4.2三种代表性工况,对流场特性、平均压力系数、流体力系数和功率谱密度曲线(Power Spectrum Density,PSD)等方面进行分析。
4.1 三维流场特性
根据Q准则[20]给出了三种间距比工况下的瞬时三维涡量图。由图3可知,流体经过圆柱体群时会随着间距比的增大而展现出不同形态,从圆柱体上脱落的漩涡会随着流体的运动慢慢扩散。间距比的增大使得下游圆柱体对上游圆柱体的阻碍会越来越小,圆柱体之间的互扰效应也会逐渐减弱。为了能够更好地显示涡脱落随间距比的变化,根据Zhang等[21]提出的波纹状剪切层(Corrugated Shear Layer,CSL)和尾涡第一次卷起位置(First Roll Up,FRU)进行表示。如图所示,剪切层开始是均匀有序的,由于三维圆柱绕流存在一定的随机性使得剪切层后方会形成波纹状剪切层,下游圆柱体的阻碍会使得波纹状剪切层发生较大的变化,产生的区域也会扩大。根据FRU的位置可以看出间距比的影响,随间距比的增大,FRU分别会在下游圆柱、中游圆柱和上游圆柱产生,表明当超过临界间距比时,各圆柱体与单圆柱体类似,漩涡有规律地脱落。上游圆柱体的漩涡撞击到下游圆柱体并与其尾流融合在一起,从而使得下游圆柱体的涡街宽度扩大。

图3 不同间距比下,圆柱体三维涡量侧视图(Q=5)Fig.3 Three-dimensional vorticity side view of circular cylinder with different spacing ratios(Q=5)
图4~6分别给出了三个特殊间距比工况下沿展向方向不同高度处的时均流线图和时均压力分布情况。由图所示,圆柱体群上分离出来的漩涡会随着间距比及截面高度的变化而呈现出不同形态,对流场产生了不同程度的扰动,上游圆柱体对下游圆柱体的影响模式会发生变化,导致时均压力分布和数值发生明显变化,因而能够较好地解释圆柱体群结构在湍流作用下的三维效应。
当L/D=1.5时,由于圆柱体之间的间距较小,上游圆柱体生成的剪切层会附着在中游圆柱体表面,中游圆柱体的剪切层也会附着在下游圆柱体表面。涡脱落现象仅在下游圆柱体尾流区发生,如图4所示。在串列双圆柱体绕流问题研究时也有类似的发现,当小于临界间距比时,上游圆柱体的剪切层附着在下游圆柱体表面上,涡脱落只在下游圆柱体产生[22]。在来流作用下,上游圆柱体因正对来流其迎流面会形成正压区,而上中游两圆柱体之间的流体因受空间限制而无法充分发展,会在间隙区内形成负压区,楼小峰等[23]对圆柱体之间形成负压区也有类似的发现。由于中游圆柱体的阻挡作用,中下游圆柱体间隙区出现零压现象,故流场出现压力差。

图4 L/D=1.5时,时均流线图与时均压力随展向高度的变化Fig.4 Variation of the time average streamline and averaged pressure with axial height at L/D=1.5
随着间距比的增大(L/D=3.0),使得上游圆柱体的剪切层会卷起形成漩涡再附着在中游圆柱体表面,但中游圆柱体的剪切层不会再附着在下游圆柱体表面,而是形成漩涡撞击下游圆柱体。Harimi等[2]在研究串列三圆柱体时均流线图时也发现了类似现象。另一方面,中游圆柱体的迎流面因受间隙区漩涡的附着,导致其漩涡尺寸和涡街宽度均变小。同时,下游圆柱体对中游圆柱体的影响逐渐减弱,使得上中游圆柱体周围流场运动与串列双圆柱体工况类似。由图5可知,上游圆柱体迎流面仍然为正压区,上中游圆柱体之间的负压区范围变大,但压力值会有所减少,在下游圆柱体迎流面则会出现正压区。

图5 L/D=3.0时,时均流线图与时均压力随展向高度的变化Fig.5 Variation of the time average streamline and averaged pressure with axial height at L/D=3.0
随着间距比进一步增大,柱体之间的相互影响会慢慢减弱,各圆柱体尾流区均会出现涡脱落现象,相关研究中也有类似现象的报道[2-5],如图6所示。上方圆柱体脱落的漩涡会直接撞击到下方圆柱体,故上方圆柱体的尾流对下方圆柱体流场和漩涡的形成仍然有一定影响。由于各圆柱体尾流均能充分发展,使得圆柱体之间的间隙区域由负压区转变为正压区,且负压区只在涡脱落区域形成。另外,随着间隙区漩涡影响的消失,中游圆柱体后方的涡街宽度明显增大。

图6 L/D=4.2时,时均流线图与时均压力随展向高度的变化Fig.6 Variation of the time average streamline and averaged pressure with axial height at L/D=4.2
4.2 时均流速
为了分析不同间距比工况下,串列三圆柱体尾流区不同位置的流场特征,本节在Z/H=0.50高度平面流场中布置相应的监测线,见图7。

图7 不同间距比下,柱体后方监测线布置Fig.7 Monitoring line layout behind the cylinder with different spacing ratios
串列三圆柱体尾流区不同位置处的时均流速分布特性,与单圆柱工况的结果进行对比分析,如图8与图9所示,u、v分别代表顺流向与横流向的速度。

图8 监测I处,时均速度分布随间距比的变化Fig.8 Average velocity distribution varying with the spacing ratio at Position I
上游圆柱体和单圆柱体的近尾流区(x/D=0.58处)顺流向时均流速分布剖面均呈“U”型,如图8(a)所示。在-0.5<y/D<0.5区域,上游圆柱体近尾流区顺流时均流速显著下降,而在中下游圆柱体近尾流区顺流时均流速下降相对缓和,且速度剖面近似为“V”型,如图8(b)和8(c)所示。此外,在-2.0<y/D<-0.5或0.5<y/D<2.0区域,上游圆柱体近尾流区顺流向时均流速会略微增加,而中下游圆柱基本保持不变。由流场分布图可知,上游圆柱体会受到来流的冲击作用,使得其柱体周围流体扰动较大。特别是在靠近柱体的区域,由于剪切层的存在会使得时均流速略微增加。同时,上下剪切层包裹区域即为阻碍区域,故上游圆柱体近尾流区顺流向时均速度下降显著。当L/D≤3.0时,间隙区漩涡的存在对流体起到了一个屏蔽作用,使得流体冲击中游和下游圆柱体的程度大大减弱,柱体周围流体的扰动也较为轻微。当L/D=4.2时,间隙区漩涡消失,上方圆柱体的尾流成为下方圆柱体的主要影响因素,这是导致下游圆柱体近尾流区顺流向时均速度分布发生变化的原因之一。同时,中游圆柱体的尾流并未直接撞击下游圆柱体,而是从下游圆柱体侧上方尾流区流过,如图6(b)所示。
由图8(d)~(f)可知,串列三圆柱体近尾流区(x/D=0.58处)横流向流速分布均会在y/D=±0.5处有一个跳跃,如图4(b)所示,这是由于该位置处于剪切层范围内会使得流体产生剪切力,而剪切力的存在则会使流体产生一个速度梯度。此外,除上游圆柱体在L/D=3.0工况外,各圆柱体近尾流区横流向时均流速分布均关于y/D=0反对称,表明柱体漩涡脱落模式呈对称分布。然而,L/D=3.0工况下,上中游圆柱体间隙区的漩涡呈现非对称性,如图5(b)所示。另一方面,三圆柱体近尾流区横流向时均流速分布随间距比的增大会发生显著变化。上游圆柱体的时均流速幅值会随着间距比的增大而减弱,如图8(d)所示。这是由于间隙区的漩涡运动,会加剧流体的流动。当间距比超过一定数值后,间隙区漩涡会往下游传播。然而,随着间距比的增加,中游圆柱体近尾流区横流向流速幅值会增大,如图8(e)所示。这是因为中游圆柱体在小间距工况下,其近尾流区横流向时均流速会受间隙区漩涡与自身尾流涡脱落的共同影响,而间距比较大时,上游圆柱体的尾涡会直接撞击中游圆柱体。小间距比工况下,由于间隙区漩涡的影响较大,下游圆柱体的近尾流区横流向尾流时均流速变化趋势基本一致,且越靠近柱体时流速越大,如图8(f)所示。当L/D=4.2时,下游圆柱体的近尾流区横流向时均流速会受到中游圆柱体的尾流及自身涡脱落的影响,使得其变化较明显,与中游圆柱体类似。由此表明,间隙区漩涡的存在对下游圆柱体的尾流形态有较大影响。
随着监测位置远离柱体(x=0.5L),流场速度的分布曲线会发生明显变化,如图9所示。当L/D=1.5时,上游圆柱体尾流区顺流向时均流速分布曲线由“U”型向“V”型转变。随着间距比的增大,顺流向时均流速分布呈现“深V”型(L/D=3.0)与浅“V”型(L/D=4.2)。值得注意的是,除L/D=4.2工况外,其它工况的顺流向时均流速的最小值均为负。这是由于随着间距比的增大,远尾流区的流体受到扰动的程度会减弱。另外,当L/D≤3.0时,间隙区的中间流体的运动发生了转向,从而导致流速出现负值,如图4(b)和5(b)所示。中游圆柱体远尾流区顺流向时均流速分布与上游圆柱体类似。然而,下游圆柱体的尾流区不存在阻碍柱体,故其流速均为正。另一方面,当L/D=4.2时,各圆柱体远尾流区顺流向时均流速分布基本趋于一致。这是因为当间距比超过临界间距比时,上中游圆柱体之间的间隙区漩涡发展充分后会往下游传播,各圆柱体与单圆柱体工况类似。

图9 监测II处,时均速度分布随间距比的变化Fig.9 Average velocity distribution varying with the spacing ratio at Position II
由图9(d)~(f)可知,在L/D≤3.0时,上游圆柱体尾流区监测位置横流向时均速度会关于y/D=0反对称,而当L/D=4.2(即x/D=2.1)时,反对称分布不再明显。这是因为当L/D≤3.0时,监测位置处的漩涡呈对称分布。然而,当L/D=4.2时,该处尾流区的漩涡呈交替脱落,且会随着尾流逐渐扩散。此外,在L/D≤3.0工况下,上游圆柱体尾流区监测位置横流向时均流速其速度幅值较小。然而,当L/D=4.2时,时均速度较大且分布较为复杂,如图9(d)所示。这是因为当间距比较小时,监测位置处漩涡的出现导致流体运动主要以顺流向为主。同时,间隙区漩涡的存在使得该区域的流体运动比较紊乱。
间距比的变化对中游圆柱体尾流区监测位置横流向时均速度分布的影响较大,如图9(b)所示。监测位置横流向时均速度曲线由关于y/D=0非对称分布(L/D=1.5)逐渐转变为反对称分布(L/D=3.0,4.2)。这是因为中游圆柱体周围流场分布特性发生了改变所致,在L/D=1.5工况下,中游圆柱体会受到间隙区漩涡的影响,而L/D=3.0工况下则主要受到尾流的影响,如图4(b)和图5(b)所示。另一方面,不同间距比工况下,下游圆柱体尾流区监测位置横流向时均速度的分布曲线形状基本一致,且曲线均关于y/D=0反对称。在小间距工况下,下游圆柱体尾流区的漩涡强度较大,导致-1.0≤y/D≤1.4范围内横流向时均速度幅值较大。
为进一步解释流体与圆柱体结构群之间相互作用的内在机理,选取三种不同间距比工况下Z/H=0.5截面处的湍动能(Turbulent Kinetic Energy,TKE)分布特性进行分析,其中ETK=(u'2+v'2+w'2)/2U∞2。由图10(a)可知,小间距比工况下,ETK最大值主要分布在中下游圆柱体尾流区,上游圆柱体则接近于零。这主要是由于中下游圆柱体的存在抑制了上游圆柱体尾流的发展,并且上游圆柱体的剪切层附着在中游圆柱体上导致自身尾流区被屏蔽,如图4(b)所示,其顺流向速度也会发生突降,如图8(a)和9(a)所示。中游圆柱体因受到上游圆柱体的剪切层的干扰,其尾流流场会发生扰动,故导致ETK分布有所变化。另外,下游圆柱体尾流区ETK的分布显著增大,主要是因为下游圆柱体存在漩涡脱落。当L/D=3.0时,上中游圆柱体尾流区的ETK值依然较小,而下游圆柱的ETK分布的最大值位置会靠近柱体表面处,如图10(b)所示。主要是中游圆柱体脱落的漩涡会撞击到下游圆柱体表面,而上中游间隙区漩涡的存在则会减弱中游圆柱体的尾流强度,图8(b)中顺流向速度下降缓和也表明流体强度有所减弱。随着间距比增大至4.2(图10(c)),三柱体尾流区均出现较为明显的ETK分布区域。并且上游圆柱体与中下游圆柱体相比,其ETK最大值出现在涡脱落区域,这是因为漩涡脱落的产生导致流场发生较大扰动。

图10 不同间距比工况下柱体群湍动能分布Fig.10 Turbulent kinetic energy of three cylinders arranged in tandem with different spacing ratios
4.3 表面压力系数
图11给出了串列三圆柱体在五种间距比工况下,0.25H、0.5H和0.75H三个高度处截面平均压力沿圆周的分布特性。由图可知,圆柱体表面压力沿圆周为对称分布且三种截面高度处的压力分布较为类似,故本节仅主要以Z/H=0.5截面进行分析。


图11 圆柱体表面平均压力系数随间距比的变化Fig.11 Variation of the average pressure coefficient on the surface of the cylinders with spacing ratio
由图11(d)可知,上游圆柱体表面压力的分布随间距比的增大无明显变化,仅数值大小有所差异,且与单圆柱的压力分布类似。其正对来流处的平均压力值最大,之后随θ的增大逐渐减小,在θ=70°或290°附近压力达到最小值,对应于上游圆柱体剪切层分离的位置,然后随θ的增大先增大再趋于稳定。平均压力分布特性会在L/D=4.1~4.2工况下发生突变。
由图11(e)可知,中游圆柱体表面平均压力的分布随间距比的增大有明显变化。在L/D≤4.1,圆柱体表面压力均为负值,且沿圆周分布有两个成对称的峰值点,对应于上游圆柱体剪切层再附着在中游圆柱体表面的位置,其数值和再附着点的位置会随着间距比的增大发生变化,由θ=67.78°(L/D=1.5)变化到θ=64.84°(L/D=4.1)。圆柱表面压力分布在L/D=4.1~4.2发生突变,在峰值点处压力变为最小。此后与单圆柱压力分布类似,随间距比的变化不大,但数值偏低。
由图11(f)可知,下游圆柱体表面平均压力的分布只在L/D=1.5有两个成对称的峰值点,且圆柱体表面压力为负,表明中游圆柱体的剪切层只在此间距比下再附着在下游圆柱体表面,其θ=43°或317°。其余各工况的压力分布与单圆柱类似,在L/D≤4.1,压力系数随着间距比的增大而增大,在L/D=4.1~4.2范围内数值会突然下降,此后会有略微变化(L/D=6.0)。
4.4 流体力系数
图12(a)给出了各圆柱体的阻力系数平均值随间距比的变化情况。同时,与文献[24]的串列双圆柱体结果进行了对比分析,上游圆柱体的阻力系数平均值计算结果与Papaioannou等[24]所描述的结果非常吻合。另外,由于中游圆柱体同时受到上游圆柱体与下游圆柱体的影响,导致中游圆柱体的阻力系数平均值与文献[24]数值上存在一定的差异,但随间距比的变化趋势基本一致。
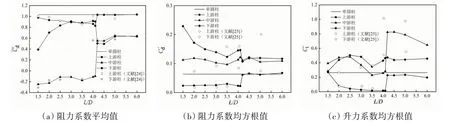
图12 串列三圆柱体表面流体力系数随间距比的变化Fig.12 Variation of fluid force coefficients of three cylinders arranged in tandem with different spacing ratios
对上游圆柱体来说,在小间距比工况下,阻力系数平均值比单圆柱体工况稍微偏低,并随着间距比的增大缓慢下降,当L/D=4.1时达到最小值。然而,当L/D=4.2时,上游圆柱体的阻力系数平均值突然增大并趋于稳定。对中游圆柱体来说,在L/D≤4.1范围内,其阻力系数平均值始终为负且随间距比的增大略微上升,在L/D=4.2工况下,其值会突变为正值。随着间距比的进一步增大,中游圆柱体的阻力系数平均值先上升再趋于稳定。上中游两圆柱体阻力系数平均值的变化趋势,可能是由于柱体之间的距离较小时,间隙区的流体会形成漩涡而产生吸力区,分别作用于上游圆柱体背流面和中游圆柱体迎流面,间距比的增大使得间隙区漩涡消失,该区域产生的吸力也会消失,如图4(b)和图6(b)所示。
对下游圆柱体来说,在L/D=1.5时,其迎流面受间隙流的影响产生了微弱的吸力,而背流面受涡脱落的影响产生了较强且相反的吸力,如图4(b)所示,故阻力系数值较低。当2.5≤L/D≤4.1时,随着间距比的增大,下游圆柱体迎流面的流场形式发生了改变,如图5(b)所示,其迎流面受中游圆柱体尾流的强烈冲击而形成正压区。同时,由于上中游圆柱体间隙区漩涡的影响,其阻力系数随间距比的增大无明显变化,故会先增大后基本平稳。当L/D>4.1时,间距比的增大使得上中游圆柱体间隙区的漩涡消除,如图6(b)所示,进而导致中游圆柱体的尾流强度变弱,加上间距的增加,下游圆柱体迎流面受到的尾流冲击更弱,故其阻力系数会突然下降。此后,随间距比的增大,圆柱体群的流场形式不再发生变化,中下游圆柱体的阻力系数趋于一致。
由图12(b)可知,当L/D≤4.1时,上游圆柱体的阻力系数均方根值会保持稳定,中游圆柱体的阻力系数均方根值变化微弱,下游圆柱体的阻力系数均方根值则是随间距比的增大而下降,并将上中游圆柱体与文献[25]串列双圆柱体进行了对比,其变化趋势类似。当L/D=4.1时,中游和下游圆柱体的阻力系数均方根值会上升,而当L/D=4.2时,除中游圆柱体外,上游和下游圆柱体的阻力系数均方根值均会发生突变。上游圆柱体的阻力系数均方根值突然增大并趋于单圆柱工况。然而,下游圆柱体的阻力系数均方根值的变化正好相反,会出现突降,最终逐渐趋于稳定。另外,上游圆柱体的均方根值均小于中游和下游圆柱体,这是因为上游圆柱体尾流的扰动会影响下游圆柱体阻力系数的波动。
串列三圆柱的升力系数均方根值随间距比的变化趋势与阻力系数均方根值基本一致,如图12(c)所示,并与文献[25]串列双圆柱体进行了对比,其变化趋势类似。在任意间距比下,上游圆柱体的升力系数均方根值均小于中游和下游圆柱体。当L/D≤4.1时,上游圆柱体升力系数均方根值随间距比的增大会逐渐下降,对中游和下游圆柱体而言,其值则会先增大后减小再增大。在L/D=4.2工况下,各圆柱体的升力系数波动均会增大,尤其是中游圆柱体的增幅最大,由图10(c)可知,湍动能分布的变化表示流场发生了较大扰动,进而导致流体力发生突变。随着间距比的增大,上游和下游圆柱体的升力系数均方根值会逐渐趋于稳定。值得注意的是,当间距比较大时,中游圆柱体的升力系数的波动会强于其他圆柱体。这是因为流场分布特性的改变,使得中游圆柱体的升力系数受到的干扰远大于其它圆柱体。
4.5 PSD曲线
图13分别给出了不同间距比下各圆柱体升力系数的PSD曲线,能够很好地对各圆柱体的涡脱落频率进行分析。由图可知,上游圆柱体在2.5≤L/D≤4.1时,其PSD曲线中存在多个频率成分,其余间距比工况只存在唯一的主频率。另外,上游圆柱体在存在多峰的工况下其谱峰值相对较小,表明流场非常紊乱,圆柱体之间的相互影响较强,涡脱落没有规律的产生和发展。值得注意的是,在大间距比工况下,下游圆柱体的PSD曲线不同于上中游圆柱体,会出现多个频率成分,此时流场和柱体之间的影响已逐渐减弱,表明峰值频率不仅与流场有关可能还与圆柱体本身的涡脱落相关。

图13 不同间距比时,三圆柱体升力系数PSD曲线的变化Fig.13 Power spectrum density(PSD)of lift coefficients on three cylinders at different spacing ratios
另一方面,串列三圆柱体的峰值频率(即涡脱落频率)均相同,相关文献中也报道了类似结论[3,8,10-11],且其数值会随间距的增大而增加。当L/D=1.5时,圆柱体的峰值频率最低,f=1.147 Hz,即斯托罗哈数为0.114 7。小间距下,圆柱体群类似于单圆柱体绕流,涡脱落只在下游圆柱体产生,如图3(a)所示。当2.5≤L/D≤4.1时,圆柱体峰值频率几乎恒定在某一数值,表明间距比的增大减弱了间隙流对圆柱体的影响,然而,中游圆柱体尾流对下游圆柱体漩涡的影响逐渐增强,如图3(b)所示,导致三圆柱体的峰值频率会增大。当L/D>4.1时,圆柱体的峰值频率先是突然增大随后逐渐稳定在2.13 Hz左右,即斯托罗哈数为0.213,表明此时上游圆柱体脱落的漩涡会随着流体的运动撞击到下游圆柱体并会影响其漩涡的发展,如图3(c)所示,导致三圆柱体的主峰值频率保持一致。
5 结 论
基于Flunet流体计算平台,本文对Re=3 900时串列三圆柱体群进行了数值模拟,然后对不同间距比工况下流场特性与柱体所受流体力进行了分析,并阐明其互扰效应机理。主要结论如下:
(1)串列三圆柱体结构群流场特性发生突变的范围L/D=4.1~4.2,导致其所受流体力会发生显著变化。
(2)上游圆柱体受到流体的冲击最大,其阻力系数平均值大于中下游圆柱体,而升阻力系数均方根值则相反。此外,尾流速度分布和表面压力分布等流场特性与单圆柱工况类似。
(3)中游圆柱体的流场特性最为复杂,小于临界间距比时,柱体迎背流面流场均为负压区,压力系数和阻力系数均为负值,且尾流宽度较窄。大于临界间距比时,流场特性和流体力系数均会发生突变。
(4)下游圆柱体的流场特性主要受中游圆柱体尾流的影响,大于临界间距比后,其流场特性、压力系数和流体力系数等均与中游圆柱体趋于一致。
(5)三圆柱体结构群的尾涡脱落会随间距比增大显著加快,泄涡频率会由1.147 Hz增大至2.130 Hz。
