圆形区域中分散布局问题的研究

徐文洋，刘光宇，余善恩

(1.杭州电子科技大学理学院，浙江 杭州 310018；

2.杭州电子科技大学自动化学院，浙江 杭州 310018)



圆形区域中分散布局问题的研究

徐文洋1，刘光宇2，余善恩2

(1.杭州电子科技大学理学院，浙江 杭州 310018；

2.杭州电子科技大学自动化学院，浙江 杭州 310018)

摘要：圆形区域分散布局问题是一类常见的数学问题，在区域分散布局的科学研究中占据了重要的位置。针对该类问题，文中建立了两个布局模型，分别为基于目标函数最小距离最大化的布局模型、基于对数函数惩罚性特点的分散布局模型。结合圆形布局区域的对称性与布局模型，得到了两个布局相关的基本结论，并给出了证明。实例求解表明，采用了序列二次型规划方法得出的数值结果与理论吻合。

关键词：分散布局；规划模型；圆形区域

0引言

在日常生活中，为了美化环境、改善空气质量、提高人民的生活品质，人们将大小不一的圆形花坛布置在十字路口、草坪和广场等公共设施中。花坛中不仅布置了五颜六色的花卉，还种植了小型灌木。特别是小型灌木的布置对花坛的美观性、空气质量及花坛采光性的改善度起到了十分重要的作用。本文将小型灌木在花坛中的合理布局问题归结为一类非线性规划模型的求解问题。查阅文献资料发现圆形区域分散布局问题和选址问题[1-3]有相似之处，尤其是选址问题中的最大覆盖问题[4-6]，它和圆形区域分散布局问题尤为相似。然而，二者也存在一些有区别：最大覆盖问题通常会给出一些备选的布局点，从备选的布局点中选出一部分作为实际布局点，而圆形区域分散布局问题[7]的布局点可以在布局区域内任意选择。由于布局点在布局区域中的位置不确定，故难以计算任意两布局点间的实际距离，这很大程度地增加了问题的求解难度。为此，本文建立了两个数学规划模型，并提出了两个相关布局定理，用于解决该类分散布局的数学问题。

1模型建立

在给出布局模型之前，首先阐述一下“分散”在文中所指的意义。所谓“分散”就是指任意两个布局点间的距离尽可能地大，而“均匀分散”则是在分散的基础上，要求任意相邻布局点间的距离尽可能地相等，“均匀分散”在布局区域中的布局结果会比较匀称和美观。

1.1　建模基础

为了建立圆形区域分散布局模型，下面给出文中数学符号的意义说明及定义。

pi(xi,yi)：布局点pi的坐标,其中xi为横坐标,yi为纵坐标。

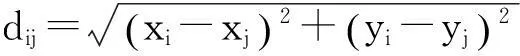
r：圆形布局区域的半径。

n：布局区域中布局点的总数。

E：标集，E={1,2,…,n}。

为了研究圆形区域最大分散化布局问题，给出如下定义：

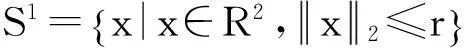
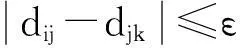
引理1[8]在圆的所有内接多边形中，正多边形的周长最长，面积最大；且随着边数n的增多而增大，当n趋于无穷时，它们分别趋向圆的周长与面积。

1.2　布局模型

以圆形布局区域中心为坐标原点，建立平面直角坐标系，分析布局点在布局区域中的布局约束条件，得出如下优化布局模型。

1)基于最小距离最大化的布局模型1

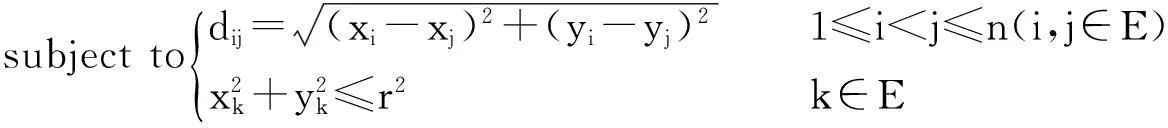
(1)

模型1是以最近两个布局点间距最大化为目标函数的非线性规划模型，所有布局点中任意两个布局点间的距离一定不小于最近的两个布局点间的距离。因此，模型1取得最优解时，布局点在圆形布局区域中必然是分散布局的。此外，模型1必有可行解。事实上，将圆形布局区域边界n等分，则布局区域边界的n个等分点就构成了模型1的一个可行解。当布局区域仅为区域边界时，由引理1可知布局点在边界上均匀分布时，布局方案具有最大的分散度，这时布局方案也是最优布局方案。

2)基于自然对数函数惩罚性的布局模型2

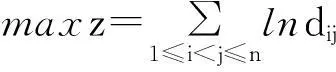
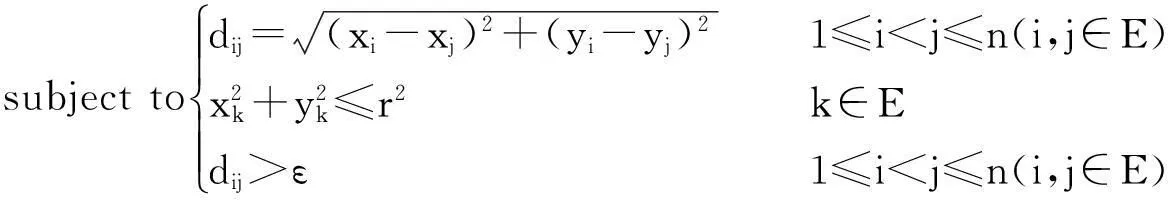
(2)

模型2是以自然对数的和函数为目标函数的规划模型，由自然对数函数的单调性可知，模型2取得最优解时，任意两个布局点都会尽可能的分散。另一方面，对数函数还具有惩罚性,要求布局区域中相邻的布局点间的距离dij,djk(i,j,k∈E)等。

模型1和模型2的目标函数不同，模型1仅考虑使布局点在布局区域中最大程度的分散，而未考虑布局后的对称性和美观性。模型2利用了自然对数的单调性和惩罚性，兼顾了布局的分散性和均匀性。因此，模型2理论上布局效果会比较均匀。进一步，由于两个布局模型均存在可行解，并且布局区域和目标函数均有上界(2r)，故两个布局模型均存在最优解。此外，参考文献[9]对该类模型最优解的存在性给出了详细的证明。

定理1布局点数n大于1时.圆形区域分散布局问题至少存在一个最优解，该最优解中至少有一个布局点分布在布局区域边界上。

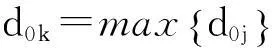
定理2布局点数n大于6时，圆形区域分散布局问题至少存在一个最优解，该最优解中至少有一个布局点分布在布局区域内部。

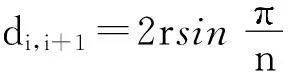
2实例分析

在R2空间中，以布局区域中心为坐标原点，地理正东与正北方向分别为x，y轴正方向，建立直角坐标系。取布局区域半径r=5m，使用序列二次规划(SQP)方法，在Matlab软件中通过编程求解模型结果如图1所示。

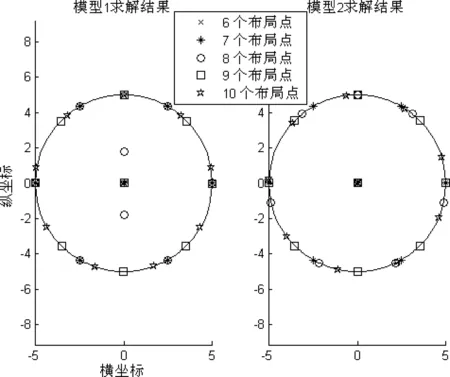
图1　模型求解结果

图1中，当布局点数n超过6时，两个布局模型的求解结果中都至少有一个布局点落在区域的内部。模型1的求解结果在n=8时，有两个布局点落在区域内部，而模型2只有一个布局点落在区域内部。此时，模型1与模型2求解布局方案的分散度分别为0.712和0.868。由于SQP方法对布局模型初始解的选取有很强的依赖性，初始解微小变化可能会对算法的迭代次数产生很大的影响，从而影响计算时间。此外，通过试验发现，当布局点数不超过15时，使用SQP方法求解模型1的计算时间多于模型2的计算时间；当布局点数较多时，使用SQP方法求解模型1的计算时间少于模型2的计算时间，具体比较如表1所示。

表1　不同布局点下两类模型计算时间比较　s

表1中，当布局点数分别为12和18时，模型1与模型2的计算时间最大，是由于这时算法迭代次数最多，分别为40次和96次。此外，一般情况下SQP方法求解模型得到的只是局部最优解，且其对初始解有很强的依赖性。因此，要彻底解决圆形区域分散布局问题需要改进原有的一些方法或提出新的解法。

3结束语

本文建立了圆形区域分散布局数学模型，给出了详细的问题描述及相关布局结论，并结合实例验证了利用模型布局的合理性，为圆形区域分散布局提供了理论依据，但未能给出模型的求解方法，故圆形区域分散布局问题有待进一步完善。

参考文献

[1] 蔡丽艳.不确定性物流中心选址问题研究[J].物流科技,2013，36(6)：64-68.

[2]从峰，耿娜，顾一韬，等.确定需求下的家庭护理中心网络选址问题研究[J].工业工程与管理,2013,18(1)：41-45.

[3]陈明.基于空间连续需求的最大覆盖选址模型及应用[J].物流技术,2014,33 (3),169-175.

[4]王维，苏经宇，马东辉，等.城市避震疏散场所选址的时间满意覆盖模型[J].上海交通大学学报,2014,48(1):154-158.

[5]Sturdy I,Kincaid R.The Robust Maximum-Coverage Problem[C]//Systems and InFormation Engineering Design Symposium (SIEDS),2014.Charlottesville：IEEE,2014:38-41.

[6]Fan X,Li V O K.The probabilistic maximum coverage problem in social networks[C]//Global Telecommunications ConFerence (GLOBECOM 2011),2011 IEEE.Houston：IEEE,2011:1-5.

[7]Wang Y,Shi Y,Teng H.Scatter Search For Constrained Layout Optimization Problem[C]//Natural Computation,2007.ICNC 2007.Third International ConFerence on.Haikou：IEEE,2007:100-104.

[8]李洁.“割圆术”蕴涵的两个结论[J].中学数学研究,2007,(10)：18-19.

[9]宋永明.无穷维规划最优解的存在性[J].成都大学学报(自然科学版),2008,27(1)：28-29.

Research oF the Scattered Layout Problem in Circular Zone

Xu Wenyang1， Liu Guangyu2， Yu Shanen2

(1.SchooloFScience，HangzhouDianziUniversity，HangzhouZhejiang310018，China;

2.SchooloFAutomation，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Abstract:Scattered layout problem is a class oF common mathematical problem in the Field oF decentralized layout scientiFic research occupied an important position. To solve such problems， we established two decentralized layout programming models. The one is based on the principle oF Max Min， the other is on the basis oF the penalty property oF logarithmic Function. There are two relevant conclusions be proposed through the analysis oF the layout models and proved in detail. With concreted examples， the results using SQP method derived are consistent with the theoretical. ThereFore， the programming models and theories presented in this paper possessed important guiding signiFicance oF actual dispersed layout problems．

Key words:scattered layout; programming model; circular area

中图分类号：O221

文献标识码：A

文章编号：1001-9146(2015)03-0093-04

通信作者:

作者简介：徐文洋(1989-)，男，安徽亳州人，在读研究生，优化理论与应用.刘光宇教授,E-mail: g.liu@hdu.edu.cn.

收稿日期：2014-09-18

DOI:10.13954/j.cnki.hdu.2015.03.020