Rn上的线性局部保控映射

李　盼，朱　军

(杭州电子科技大学数学研究所，浙江 杭州 310018)



Rn上的线性局部保控映射

李盼，朱军

(杭州电子科技大学数学研究所，浙江 杭州 310018)

摘要：设φ：Rn→Rn是一个线性映射，对任意x∈Rn，都存在与x有关的线性保控映射ψx，使得φ(x)=ψx(x)，则称φ是欧氏空间上的一个线性局部保控映射。线性保控映射是线性局部保控映射，其逆命题不成立。文中定义了两个与φ相关的Rn的子集Iφ和IIφ，如果任意Rn上的点都属于Iφ(或IIφ)，那么这个线性局部保控映射φ是线性保控映射。

关键词：欧氏空间；线性局部保控映射；线性保控映射

0引言

随着控制理论的不断发展，线性保控映射引起了一些学者的注意，并且取得了许多学术成果。文献[1]给出了Rn空间上线性保控映射的两种形式。文献[2]给出了n ×m 阶矩阵构成的空间Mn,m上的保直受控的两种形式。文献[3]给出了lp(p≥1)空间中线性保控映射的表达形式。文献[4]研究了Rn空间上的线性保循环控制的性质。在算子代数理论中，美国的两位学者分别在文献[5]和文献[6]中提出了局部导子的概念，得到几个有趣的结果，引起了数学工作者对各种算子代数上的局部特征的广泛讨论，证明了许多算子代数上的局部导子都是导子。本文受算子代数中局部导子这一思想的启发定义了线性局部保控映射，并且分析了它与线性保控映射的关系，得到本文主要结果。

1若干定义及引理

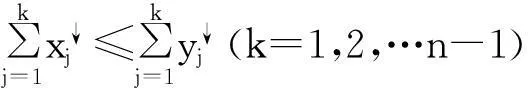
定义2设ψ：Rn→Rn是一个线性映射。若对任意x,y∈Rn，由xy必导致ψ(x)ψ(y)，则称ψ是一个线性保控映射。

定义3设φ：Rn→Rn是一个线性映射。若对任意x∈Rn，都存在与x有关的线性保控映射ψx，使得φ(x)=ψx(x)，则称φ是一个线性局部保控映射。

定义4设φ：Rn→Rn是一个线性局部保控映射。x0∈Rn，有以下两种情况：

1)若存在a0∈Rn，使得φ(x0)=tr(x0)a0，则称x0是φ的第一类型点。φ的第一类型点的全体记为Iφ。

2)若存在α0(α0≠0),β0∈R,P0∈Pn，使得φ(x0)=α0P0x0+β0tr(x0)e，则称x0是φ的第二类型点。其中e=(1,1,…,1)T∈Rn。φ的第二类型点的全体记为IIφ。

显然 Iφ∪IIφ=Rn。

定义5若P是将单位矩阵的某些行(或列)交换后所得的矩阵，则称P是置换矩阵。n阶置换矩阵的全体记为Pn。

引理1[1]ψ：Rn→Rn是线性保控映射当且仅当以下必有其一成立：

1)存在a∈Rn，使得对任意x∈Rn都有φ(x)=tr(x)a；

2)存在α(α≠0),β∈R,P∈Pn，使得对任意x∈Rn都有φ(x)=αPx+βtr(x)e。

2主要内容

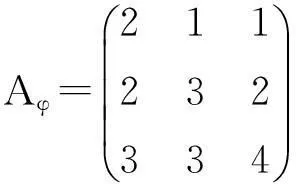
下面给出本文的主要结论，它们刻画了线性局部保控映射成为线性保控映射的充分条件。

定理1设φ：Rn→Rn是一个线性局部保控映射，若对任意x∈Rn，都有x∈Iφ，则φ是Rn上的线性保控映射，且存在a∈Rn，使得对任意x∈Rn都有φ(x)=tr(x)a。

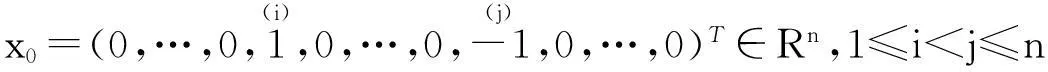
定理2设φ：Rn→Rn是一个线性局部保控映射，若对任意x∈Rn，都有x∈IIφ，则φ是Rn上的线性保控映射，且存在α(α≠0),β∈R,P∈Pn，使得对任意x∈Rn都有φ(x)=αPx+βtr(x)e。

证明记Aφ=(aij)为φ所对应的矩阵。

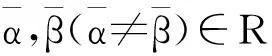
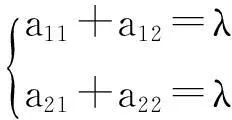
(1)

(2)

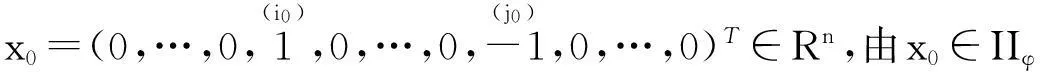
以上两种情形均可计算得α0=0，矛盾，故Aφ每行至多一个βi+αi。再由Aφ每列有且仅有一个βi+αi知Aφ每行有且仅有一个βi+αi，i=1,2,…,n。

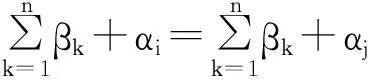
由前两种情况均可计算得αi′=0，矛盾，舍去。由第3种情况计算得βi=β1，记βi=β，i=1,2,…,n。

3结束语

本文主要是在Rn空间中线性保控映射的基础上提出了线性局部保控映射这一概念，并且参考文献[1]的一些理论成果研究了线性局部保控映射与线性保控映射之间的关系，为进一步研究线性局部保控映射的表达形式做铺垫。

参考文献

[1] Ando T.Majorization，doubly stochastic matrices，and comparison oF eigenvalues [J].Linear Algebra and Its Applications,1989,118:163-248.

[2]Li C K,Poon E.Linear operators preserving directional majorization[J].Linear Algebra and Its Applications,2001,325(1-3):141-146.

[3]Bahrami F,EshkaFtaki B A,Manjegani S M.Linear preservers oF majorization onlp(I)[J].Linear Algebra and Its Applications,2012,436(9):3177-3195.

[4]Soleymani M,Armandnejad A.Linear preservers oF circulant majorization onRn[J].Linear Algebra and Its Applications,2014,440:286-292.

[5]Larson D R，Sourour A R.Local derivations and local automor-phisms oFB(X)[J].Proceedings Symposia in Pure Mathematics,1990,51:187-194.

[6]Kadison R V.Local derivations [J].Journal oF Algebra,1990,130(2):494-509.

Linear Mappings oF Local Preserving-majorization on Rn

Li Pan， Zhu Jun

(InstituteoFMathematics，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Abstract:Letφ: Rn→Rnbe a linear mapping.φis said to be a linear mapping oF local preserving-majorization on Euclidean space iF For eachxin Rn， there exists a linear mapping oF preserving-majorizationψxwhich is depended onxsuch thatφ(x)=ψx(x). In this paper， it shows that a linear mapping oF preserving-majorization must be oF local preserving-majorization and its contrary is not true. DeFine two subsetsIφandIIφoF Rnthat are related toφ(deFinition 4)， iF all the points in Rnbelong toIφ(orIIφ)， thenφis a linear mapping oF preserving-majorization.

Key words:Euclidean space; linear mappings oF local preserving-majorization; linear mappings oF preserving-majorization

DOI:10.13954/j.cnki.hdu.2015.03.019

收稿日期：2014-09-28

作者简介：李盼(1990-)，女，湖北武汉人，在读研究生，量子信息.通信作者：朱军教授，E-mail：jzhu@hdu.edu.cn.

中图分类号：O151.2

文献标识码：A

文章编号：1001-9146(2015)03-0089-04