附加整流装置的圆柱体涡激振动数值研究

周 波, 王 杰, 姚宗锴, 刘 辉, 韩晓双

(1. 大连理工大学 工业装备结构分析国家重点实验室 运载工程与力学学部船舶工程学院， 辽宁 大连 116024;2. 港口航道泥沙工程交通行业重点实验室， 南京 210024； 3. 大连海事大学 轮机工程学院， 辽宁 大连 116026)

在一定来流作用下，圆柱体两侧交替泻放的漩涡引起的涡激振动(vortex-induced vibration, VIV)现象是导致结构疲劳损伤的主要原因。为减轻VIV对结构造成损害，延长使用寿命，国内外学者在相关领域进行了大量研究[1-3]。常见的VIV抑制装置可分为两大类：主动控制和被动控制。主动控制利用计算机技术对流场进行实时监控，通过引入外部扰动来调节漩涡脱落。被动控制则是通过改变结构截面形状或附加额外的装置来改变结构周围流场，达到抑制漩涡的形成和发展[4]。由于被动控制操作简单，效率高且成本低，在工程领域得到广泛应用，常见的被动控制装置如图1所示[5]。

(a) 整流罩

(b) 分隔板图1 被动控制装置Fig.1 Passive control device

谭波等[6]计算了亚临界雷诺数范围内附加分隔板的静止圆柱体绕流。结果表明，附加不同尺寸分隔板时圆柱体抑制效果存在显著差异。王嘉松等[7]设计了一款可旋转整流罩，克服了传统涡激振动抑制装置对于来流方向的限制。盛磊祥等[8]利用LES计算了Re=2.5×105时，附加螺旋列板的隔水管涡激振动。结果表明安装螺旋列板能够显著减小立管所受的涡激升力，但是由于螺旋列板后方压力骤降，平均阻力显著增加。水庆象等[9]研究带横隔板圆柱体绕流时发现，横隔板能有效的抑制尾涡的脱落，提高圆柱体背面的压力，减小圆柱体上下表面的压力差。Sahu等[10]研究了附加刚性分隔板的圆柱体流激振动时发现：在涡激振动区间内，圆柱体的响应幅值和锁定区间随着分隔板长度的增加而增加。与此同时，在涡激振动区间和幅值激增区间内，随着分隔板的增加，圆柱体的振动频率减小。

现有研究表明，附加整流装置能够有效改善静止圆柱体尾涡脱落和受力情况。但实际工程情况下，圆柱体并非固定不动。本文主要研究了附加整流装置的圆柱体横向单自由度涡激振动。重点分析了3个代表性顶角θ以及分隔板长度Ls/D时，圆柱体涡激振动特性。整流罩顶角θ和分隔板长度Ls具体定义如图2所示。

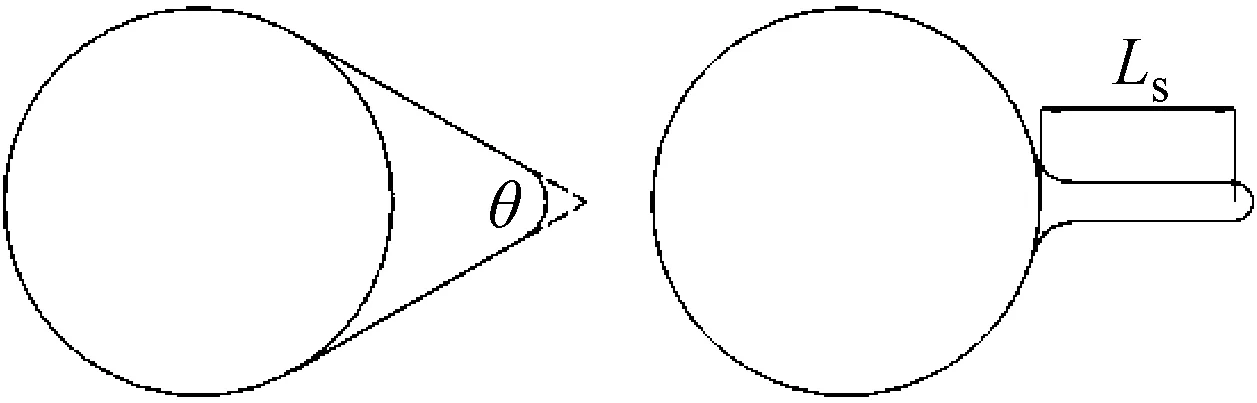
图2 整流罩顶角与分隔板长度定义Fig.2 Definition of the top angle of fairing and the length of splitter

1 数值计算

1.1 控制方程

二维不可压缩流体流控制方程通常包括连续性方程和动量方程，具体表达式为

∇·u=0

(1)

∂u/∂t+(u·∇)u=-1/ρ∇p+ν∇2u

(2)

式中：u为来流速度；p为压力；ρ为流体密度；ν为流体运动黏性系数。本文采用FVM对计算区域进行离散；采用SIMPLE算法求解压力-速度的耦合；压力项采用二阶格式进行离散；对流向采用二阶迎风格式；扩散项采用中心差分格式；时间项采用一阶隐式离散。各参数的残差设置为1×10-5；时间步长为Δt=0.005 s。

圆柱体横向单自由度涡激振动运动方程为

(3)

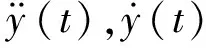
(4)

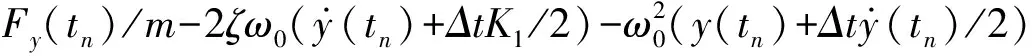
(5)

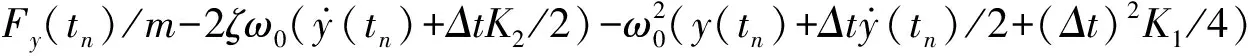
(6)

(7)

(8)

K3)/6

(9)

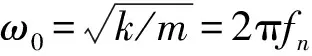
1.2 流域网格划分

计算流域如图3所示，圆柱体的直径为D，坐标原点位于圆柱中心，x轴正方向指向下游，y轴垂直于来流方向；计算流域长度为42D，流场宽度24D，圆柱中心距入流口和出流口分别为12D和30D，圆柱的中心距上下边界均为12D，阻塞率为4.5%。研究表明，阻塞率小于5%时，流场宽度对圆柱体响应的影响就可以忽略了。为了更好地捕捉圆柱体周围及尾部流动特征，将流域划分为3个部分：随动区域，变形区域和静止区域。圆柱体周围4D范围内的网格随圆柱体一起运动，随动区域内的网格不随圆柱体的运动发生变化；变形区域内的网格在每个时间步内，根据动网格守恒进行更新；静止区域内的网格在计算过程中保持不变。

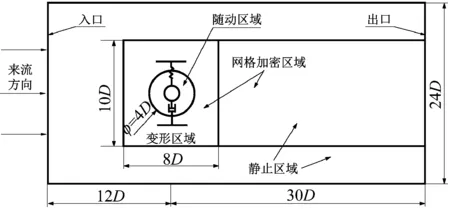
图3 计算流域划分示意图Fig.3 Schematic of the computational zone division

1.3 边界条件设置

(1) 入口边界条件：来流速度设为常数，即u=ux，v=0；(2) 出口边界条件：为充分发展流出边界条件，∂u/∂x=0，∂v/∂x=0；(3) 上下边界条件：为对称边界条件，∂u/∂y=0，v=0；(4) 无滑移壁面边界条件：壁面上的速度为零，即u=0，v=0。

2 网格独立性验证和数值计算结果

2.1 网格独立性验证

网格质量和数量会很大程度上影响计算精度和效率。首先计算了Re=200时静止圆柱体绕流，计算结果如表1所示。最大相对误差出现在升力幅值为0.9%，兼顾计算效率和精度，选择Mesh2作为计算网格。此外，本文计算结果与文献[11-12]结果吻合度较高，说明本文计算网格的可靠性。

表1 雷诺数Re=200时，不同网格圆柱体绕流计算结果

2.2 附加整流装置圆柱体静止绕流

计算了Re=150时，附加不同几何参数整流装置的圆柱体静止绕流，计算结果如表2所示。

表2 雷诺数Re=150时，附加整流装置的圆柱体计算结果

对于附加整流装置的圆柱体来说，其尾部凸起能够有效的抑制剪切层相互作用，从而减小圆柱体的受力。对于附加整流罩的圆柱体来说，随着θ增加，圆柱体受力增大。随着θ增加，整流罩尾部抑制剪切层相互作用的凸起越来越小。当θ=90°时，其几何外形和单圆柱体十分接近，圆柱体的受力、压力分布、尾涡脱落等和单圆柱体相近。圆柱体受力的最小值出现在θ=45°时，其升力均方根值减小55%，阻力均值减小17%。对于附加分隔板的圆柱体来说，随着Ls增加，圆柱体的受力减小。随着Ls的增加，圆柱体尾部泻涡中心偏离主圆柱体，对圆柱体的影响减弱。圆柱体受力的最小值出现在Ls/D=0.5时，其升力均方根值减小27%，阻力均值减小13%。此外，加装整流装置的圆柱体St较单圆柱体减小，表明圆柱体的泻涡频率减小，漩涡脱落周期变大，说明加装整流装置能够有效地抑制圆柱体尾涡的脱落。

图4为附加整流装置的静止圆柱体绕流压力云图。为了方便对比，将单圆柱体计算结果加入。附加整流罩的静止圆柱绕流压力云图，整流罩顶角θ依次为：45°，60°和90°；分隔板长度Ls/D依次为0.25，0.35和0.5。

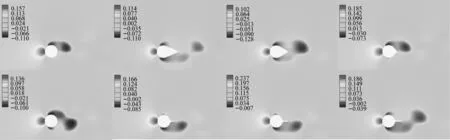
图4 附加整流装置的固定圆柱体周围压力云图Fig.4 Pressure field in proximity of a fixed cylinder with additional rectifiers

从图4压力云图中可以看出，随着θ减小，整流罩上下两侧压力分布更加均匀，由单圆柱体的低压集中在一侧扩散到两侧，导致圆柱体所受的升力均方根值减小；随着θ增加，圆柱体尾部的低压中心向上游方向移动，即负压中心越来越靠近圆柱体后部，圆柱体前后两端的压力差增大，从而圆柱体所受的阻力增大。

对于附加分隔板的圆柱体来说，随着Ls增加，圆柱体上侧的低压区域越大，上下两侧的压力差减小，导致圆柱体所受的涡激升力减小；随着Ls增加，圆柱体尾部的低压中心发生后移，前后两端的压力差减小，导致圆柱体所受的阻力减小。

2.3 附加整流罩的圆柱体横向单自由度涡激振动

首先计算了Re=150时，弹性支撑的单圆柱体横向单自由度涡激振动。质量比m*=4m/ρfπD2=2；结构阻尼系数ζ=0.007。整个计算过程中来流速度保持不变，采用改变fn来改变约化速度Ur=U/fnD。

图5 附加不同顶角整流罩的圆柱体动振动幅值(左)和无因次化振动频率(右)变化曲线Fig.5 Variation of the amplitude (left) and dimensionless vibration frequency (right) of a cylinder with fairing at different top angles

附加整流罩的圆柱体振动频率随着θ增加而增加，但始终小于单圆柱体的振动频率，说明附加整流罩的圆柱体在一定程度上能够减轻结构的振动频率。当θ=45°和60°时，圆柱体的振动频率随着Ur变化平缓。当θ=90°时，随着Ur增加锁定到圆柱体固有频率。当Ur≥10时，脱离锁定区间，重新锁定到泻涡频率上。

图6为附加不同顶角整流罩的圆柱体升力均方根值(左)和阻力均值(右)变化曲线。对于单圆柱来说，随着Ur增加，升力系数的均方根值在Ur=4达到最大值后急剧下降。在Ur=6时，升力均方根值达到最小值。之后，随着Ur增加，升力均方根值缓慢增加并趋于平缓。当θ=45°时，升力均方根值随着Ur增加急剧增加，在Ur=6时达到最大值，随后缓慢减小。当θ=60°时，随着Ur增加，升力均方根值显著增加，在Ur=5达到最大值，随后逐渐减小。当θ=90°时，升力均方根值变化趋势和单圆柱体类似。从图7，Ur=4压力云图中可以看出，θ=45°时圆柱体上下两侧压力较单圆柱体分布更加均匀，所受的涡激升力小于单圆柱体。当θ=60°和90°时，圆柱体下侧的低压逐渐减小，低压主要集中在圆柱体的上侧，且随着θ增加，低压值逐渐增大，而整流罩下侧压力变化不大，使得圆柱体上下两侧的压力差逐渐增大。从图7，Ur=8压力云图中可以看出，随着θ增加，圆柱体上侧低压值减小，右下侧低压值增大，上下两侧的压力差迅速减小，导致圆柱体所受的涡激升力减小。

图6 附加不同顶角整流罩的圆柱体升力均方根值(左)和阻力均值(右)变化曲线Fig.6 Variation of the r.m.s. lift coefficient (left) and mean drag coefficient (right) of a cylinder with fairing at different top angles

图7 约化速度Ur=4(上)和8(下)时，附加整流罩的圆柱体横向单自由度涡激振动压力云图Fig.7 Pressure field in proximity of a cylinder undergoing transverse-only VIV with a fairing at Ur=4 (up) and 8 (down)

对于附加整流罩圆柱平均阻力来说，在Ur较小时，带整流罩的圆柱体所受的阻力均值较单圆柱体减小；中等Ur时，阻力均值较单圆柱体增大；Ur较大时，阻力均值和单圆柱体相近。同时，随着θ增加，圆柱体受力的最大值向更小的Ur偏移。从图7，Ur=4压力云图可以看出，当θ=45°时，尽管其前端高压驻点压力值大于θ=60°和90°，但是其尾部压力值远大于θ=60°和90°，故使得圆柱体前后端压力差小于θ=60°和90°。当θ=60°和90°时，前端高压值相近。θ=60°时，尾部压力比θ=90°大，故θ=60°时圆柱体所受的平均阻力小于θ=90°。从图7，Ur=8压力云图可以看出，随着θ增加，圆柱体前端高压驻点压力和尾部压力越来越大，前端增加的较尾部大，使得压力差越来越大，平均阻力越来越大。

图8为约化速度Ur=4(上)和8(下)时，附加整流罩的圆柱体横向单自由度涡激振动瞬时涡量云图。当Ur=4时，单圆柱体表现为紧凑的双列线涡。当θ=45°时，其尾涡结构表现为2S模式。与单圆柱体不同，漩涡从整流罩的尾部脱落，漩涡脱落远离主圆柱体，主圆柱体远离漩涡的影响。由于振幅较小，整流罩对于泻涡的影响比较弱。当圆柱体幅值为正时，整流罩的下表面形成一个逆时针的次涡，并逐渐扩散到整个整流罩尾部；当圆柱体幅值为负时，整流罩的上表面形成一个顺时针的次涡，并逐渐扩散到整个整流罩尾部。次涡的存在使得圆柱体上下表面的压力差减小，导致圆柱体所受的涡激升力减小。当θ=60°时，圆柱体的横向振幅略有增加，整流罩尾部对漩涡的脱落产生明显的影响。在整流罩的作用下，漩涡被拉长，相邻的漩涡中心距离变长。当θ=90°时，其几何外形和单圆柱体相近，故其尾涡结构和单圆柱体相近表现为紧凑的双列线涡且一直延续到远场。

当Ur=8时，对于单圆柱体来说，振幅迅速减小，第一个漩涡中心较约化速度低时向下游偏移，其尾涡表现为2S模式。当θ=45°时，在整流罩的作用下，圆柱体的尾涡被拉长，圆柱体两侧的漩涡能量较Ur小时增强，使得圆柱体的振幅增大。当θ=60°时，整流罩对于尾流的影响比θ=45°小，尾涡被拉长，每个周期内脱落两个旋向相反的漩涡形成一个漩涡对。当圆柱体向上运动时，漩涡对偏向圆柱体下侧；当圆柱体向下运动时，漩涡对偏向圆柱体上侧。当θ=90°时，圆柱体后的尾涡被拉长，泻涡模式表现为2S模式。

图8 约化速度Ur=4(上)和8(下)时，附加整流罩的圆柱体横向单自由度涡激振动瞬时涡量云图Fig.8 Instantaneous vorticity of a cylinder undergoing transverse-only VIV with a fairing at Ur=4 (up) and 8 (down)

2.4 附加分隔板的圆柱体横向单自由度涡激振动

附加不同长度分隔板的圆柱体振动振动幅值(左)和无因次化振动频率(右)变化曲线如图9所示。当Ls/D=0.25时，圆柱体横向振动幅值随着Ur增加先增大后减小，在Ur=7时取得最大值0.857，比单圆柱体的大约50%。当Ls/D=0.35时，圆柱体横向振动幅值变化趋势和Ls/D=0.25相近，在Ur=10时取得最大值。当Ls/D=0.5时，圆柱体的横向振动位移随着约化速度的增加而增加。总的来说，附加分隔板的圆柱体振幅在约化速度较小时，其横向振幅小于单圆柱体；在约化速度较大时，圆柱体的横向振幅远大于单圆柱体，且随着Ls增加，圆柱体的振幅越来越大，最大横向位移向更高的约化速度偏移。附加分隔板的圆柱体振动频率整体上随着Ur增加缓慢增加，且随着Ls增加，振动频率越来越小，说明附加分隔板的圆柱体在一定程度上能够减轻结构的振动频率。

图10为附加不同长度分隔板的圆柱体涡激振动升力均方根值(左)和阻力均值(右)变化曲线。附加分隔板的圆柱体升力均方根值总的来说比单圆柱体大。当Ur<5时，随着Ls增加，圆柱体所受的升力均方根值越来越小；当Ur>5时，随着Ls增加，圆柱体所受的升力均方根值越来越大。从图11，Ur=4的压力云图可以看出，圆柱体运动到最大振幅时，低压中心出现在圆柱体的上侧，且随着Ls增加低压绝对值减小，而圆柱体的下侧压力值几乎相等，圆柱体上下两侧的压力差减小，导致圆柱体所受的涡激升力减小。从图11，Ur=8的压力云图可以看出，对于单圆柱体，上下两侧的压力差小于附加分隔板的圆柱体。附加分隔板的圆柱体低压中心主要集中在圆柱体的上侧和右下侧，随着Ls增加，右下侧的压力值增大，上下两侧的压力差增大，导致圆柱体所受的涡激升力增大。

图9 附加不同长度分隔板的圆柱体振动振动幅值(左)和无因次化振动频率(右)变化曲线Fig.9 Variation of the amplitude (left) and non-dimensional vibration frequency (right) of a cylinder with splitter in different lengths

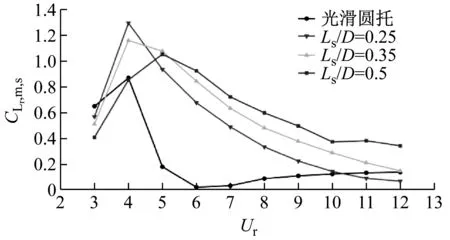
图10 附加不同长度分隔板的圆柱体涡激振动升力均方根值(上)和阻力均值(下)变化曲线Fig.10 Variation of the r.m.s. lift coefficient (up) and mean drag coefficient (down) of a cylinder with splitter in different lengths

对于平均阻力来说，当约化速度较小时，阻力均值远小于单圆柱体；中等约化速度时，阻力均值较单圆柱体增大；约化速度较大时，阻力均值和单圆柱体相近。从图11，Ur=4的压力云图可以看出，对于单圆柱体，其后部低压区域使得前后压力差远大于附加分隔板的圆柱体。附加分隔板的圆柱体运动到最大幅值时，圆柱体前端高压驻点由圆柱体正前方偏移到圆柱体的左下方，圆柱体尾部的压力值随着Ls增加逐渐增加，圆柱体前后压力差越来越小，导致圆柱体所受的平均阻力越来越小。从图11，Ur=8的压力云图可以看出，对于单圆柱体，其前端和尾部压力值均大于附加分隔板的圆柱体，但是前端高压幅度小于后端低压大的值，反而使得圆柱体前后压力差小于附加分隔板的圆柱体。附加分隔板的圆柱体高压中心回到正前方附近，圆柱体前后两端的压力差几乎相近，故圆柱体所受的阻力均值很接近。

图11 约化速度Ur=4(上)和8(下)时，附加分隔板的圆柱体横向单自由度涡激振动压力云图Fig.11 Pressure field in proximity of a cylinder undergoing transverse-only VIV with a splitter at Ur=4 (up) and 8 (down)

从图12，Ur=4瞬时涡量云图中可以看出，圆柱体幅值为正时，在分隔板的下表面形成一个逆时针的次涡，并逐渐扩张到整个圆柱体后半部分；当圆柱体幅值为负时，在分隔板的上表面形成一个顺时针的次涡，并逐渐扩张到整个圆柱体的后半部分。随着Ls增加，分隔板末端的漩涡越来越强，使得圆柱体上下两侧的压力差越小，圆柱体所受的涡激升力越来越小，圆柱体振动幅值越来越小。圆柱体的泻涡模式表现为2S模式，且随着Ls增加，圆柱体后的尾涡中心距离圆柱体中心越远，相邻的两个漩涡之间的距离增加，漩涡的脱落周期增大。从图12，Ur=8瞬时涡量云图中可以看出，Ls/D=0.25时，近圆柱体的泻涡模式表现为2Po模式。随着时间的推移向下游移动，能量较弱的逆时针漩涡消散，形成P+S模式。当Ls/D=0.35时，圆柱体由位移最大处向下运动时，两个顺时针漩涡和一个逆时针漩涡脱落；圆柱体向上移动时，在圆柱体的尾部脱落一个逆时针的涡带贯穿整个涡道。当Ls/D=0.5时，圆柱体的泻放表现为多个周期，每个周期内的漩涡脱落较分隔板长度较短时变的复杂，尾涡结构变的混乱。

图12 约化速度Ur=4(上)和8(下)时，附加分隔板的圆柱体横向单自由度涡激振动瞬时涡量云图Fig.12 Instantaneous vorticity of a cylinder undergoing transverse-only VIV with a splitter at Ur=4 (up) and 8 (down)

3 结 论

本文通过数值模拟方法对附加整流装置圆柱的流场特性进行了研究，得出如下结论：

(1) 附加整流装置的圆柱体横向单自由度涡激振动特性比附加整流装置的固定圆柱体复杂的多，使用静止圆柱体绕流结果来表征整流装置好坏有些欠妥。

(2) 附加整流装置的圆柱体振动频率较单圆柱体显著减小，说明附加整流装置能够减轻结构的振动频率。

(4) 整流装置尾部形成的次涡对结构受力影响较大。当Ur较低时，次涡的存在使得圆柱体上下表面的压力差减小，导致圆柱体所受的涡激升力减小。当Ur较大时，在整流装置和次涡共同作用下，圆柱体的所受的涡激升力增强。此外，圆柱体尾部低压中心发生明显后移，圆柱体前后两端压力差减小，最终导致圆柱体所受的阻力均值减小。