二维模糊系统的H∞性能分析

彭大蒙，周绍生

(杭州电子科技大学自动化学院，浙江 杭州 310018)



二维模糊系统的H∞性能分析

彭大蒙，周绍生

(杭州电子科技大学自动化学院，浙江 杭州 310018)

摘要：主要研究了一类基于T-S模型的带有参数不确定性的二维模糊系统的H∞性能分析问题。二维系统采用二维系统的FM模型，假定系统参数的不确定性具有线性分式结构，利用基依赖的Lyapunov函数结合不等式变换技巧，建立了满足给定性能指标的系统渐近稳定的充分条件。最后通过仿真实验验证了结果的有效性。

关键词：T-S模型；二维系统；参数不确定；H∞

0引言

二维系统的控制和信号处理一直是研究的热点，Hinamoto利用Lyapunov函数方法研究了二维系统的稳定性[1]，Du和Xie等人利用Riccati不等式方法和线性矩阵不等式研究了二维离散系统的H∞滤波问题[2]，并研究了满足给定性能指标的输出反馈控制器的设计问题[3]。当系统中存在不确定性和干扰时，H∞范数的性能指标给系统分析带来很大的便利。系统建模一直是非线性系统研究中的一个难点问题，应用T-S模糊模型可以很好地解决这一难题。这些年来，T-S模糊模型和H∞理论在二维系统的研究中得到了大量的应用[4-6]，文献[7]研究了基于T-S模型的二维系统的稳定性分析和镇定问题。文献[8]研究了带不确定性的离散模糊系统的H∞控制问题，采用基依赖的Lyapunov函数相比公共Lyapunov函数方法得到的稳定性条件具有较小的保守性，引入了一个辅助矩阵实现了矩阵之间的解耦，从而通过求解线性不等式得到所设计系统的状态反馈控制器。受此启发，本文主要研究一类基于T-S模型的二维不确定系统在有扰动存在时的H∞性能分析问题，假定系统带有线性分式不确定性，利用基依赖的Lyapunov函数结合不等式变换技巧，以线性矩阵不等式形式给出了系统稳定的充分条件。

1系统描述

考虑如下IF-Then规则描述的基于第二类 FM 模型的二维模糊系统：

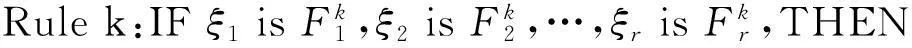
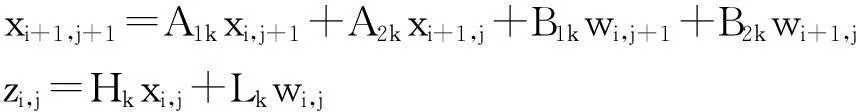
(1)

(2)

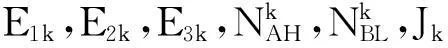
上述模糊系统可重新表示为：

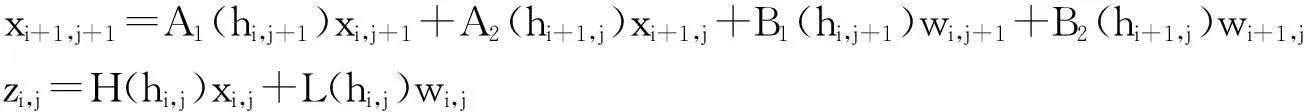
(3)

假设存在正整数T1和T2，使得边界满足下面给定条件：

(4)

定义Xr={sup‖x(i,j)‖i+j=r}，系统的稳定性可定义如下。

2主要结果

首先考虑参数确定的系统，即当不确定矩阵Fk=0时，系统描述为：

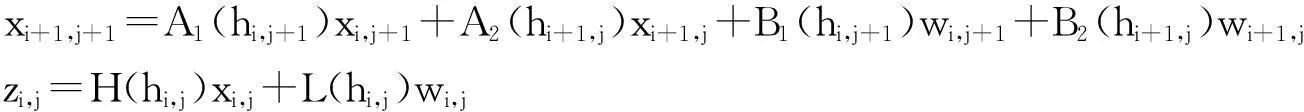
(5)

(6)

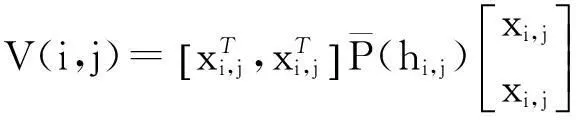
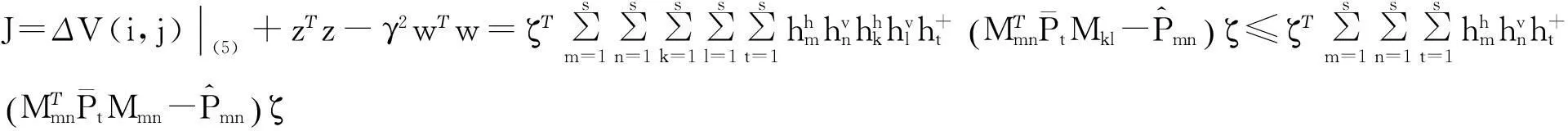
得到定义中给出的H∞性能指标成立，定理1得证。

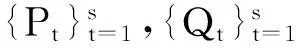
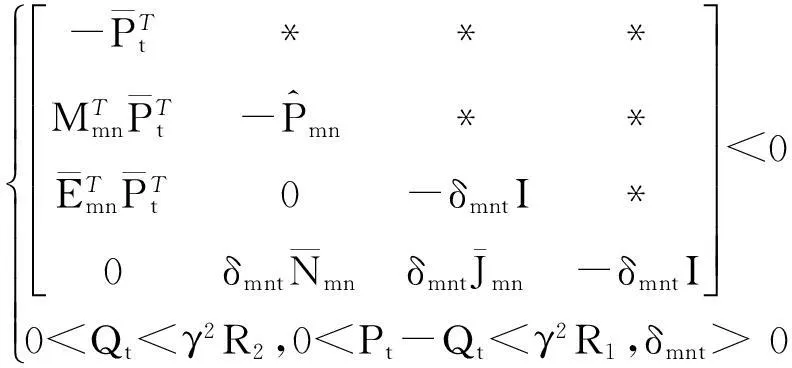
(7)

根据文献[9]中的线性分式结构不确定性的不等式定理可以得到不等式(7)成立，定理2得证。

3数值实例

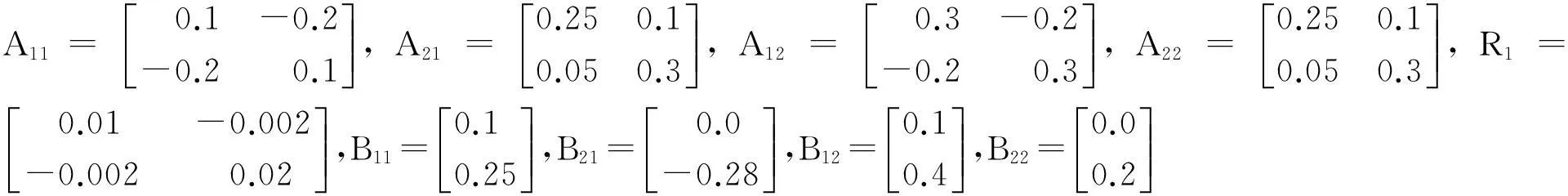
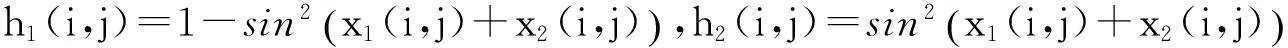
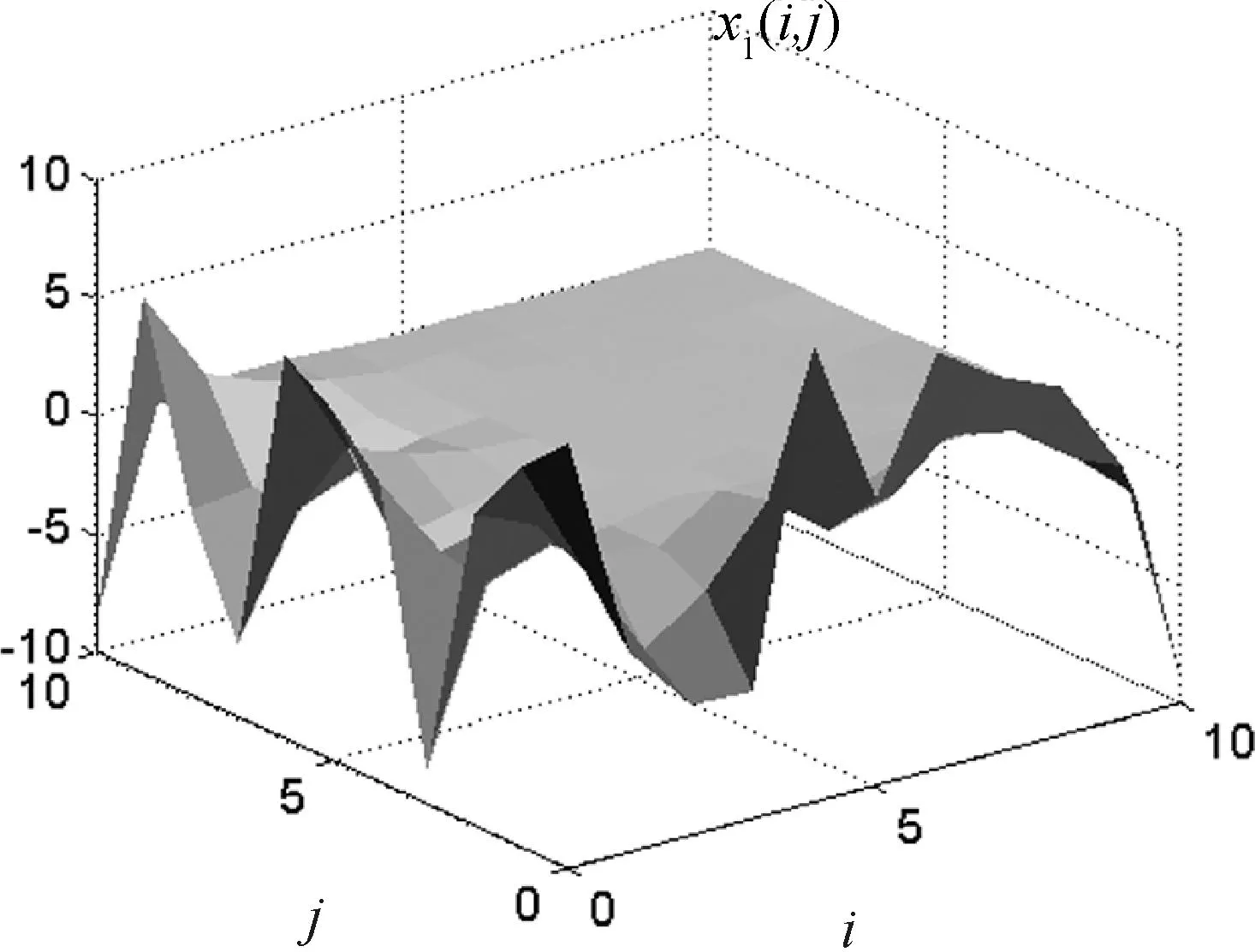
图1　系统状态响应x1(i,j)

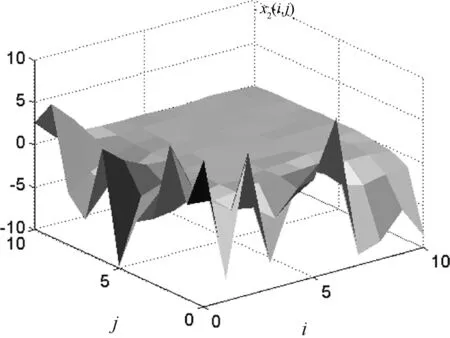
图2　系统状态响应x2(i,j)

4结束语

本文以矩阵不等式的形式给出了带有输入干扰和系统参数不确定性的二维系统的渐近稳定且具有抗干扰的H∞性能指标的充分条件。相比于公共Lyapunov函数方法，本文采用基依赖的Lyapunov函数方法得到的结果具有较小的保守性。通过仿真例子验证了设计方法的有效性。

参考文献

[1] Hinamoto T.Stability oF 2-D discrete systems described by the Fornasini-Marchesini second model[J].Circuits and Systems I: Fundamental Theory and Applications,IEEE Transactions on,1997,44(3):254-257.

[2]Du C,Xie L,Soh Y C.H∞Filtering oF 2-D discrete systems[J].Signal Processing,IEEE Transactions on,2000,48(6):1 760-1 768.

[3]Xie L,Du C,Soh Y C,et al.H∞and robust control oF 2-D systems in FM second model[J].Multidimensional Systems and Signal Processing,2002,13(3):265-287.

[4]Li L,Wang W.Fuzzy modeling and H∞control For general 2D nonlinear systems[J].Fuzzy sets and systems,2012,207:1-26.

[5]Duan Z,Xiang Z,Reza Karimi H.Stability and l1-gain analysis For positive 2D TS Fuzzy state-delayed systems in the second FM model[J].Neurocomputing,2014，142(22)：209-215.

[6]Boukili B,Hmamed A,Benzaouia A,et al.H∞Filtering oF Two-Dimensional TS Fuzzy systems[J].Circuits,Systems,and Signal Processing,2014,33(6):1 737-1 761.

[7]Chen X,Lam J,Gao H,et al.Stability analysis and control design For 2-D Fuzzy systems via basis-dependent Lyapunov Functions[J].Multidimensional Systems and Signal Processing,2013,24(3):395-415.

[8]Zhou S,Feng G,Lam J,et al.Robust H∞control For discrete-time Fuzzy systems via basis-dependent Lyapunov Functions[J].InFormation Sciences,2005,174(3):197-217.

[9]Chang X H.Robust nonFragile Filtering oF Fuzzy systems with linear Fractional parametric uncertainties[J].Fuzzy Systems,IEEE Transactions on,2012,20(6):1 001-1 011.

H∞PerFormance Analysis For 2-D Fuzzy Systems

Peng Dameng， Zhou Shaosheng

(SchooloFAutomation，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Abstract:This paper deals with H∞perFormance analysis For two-dimensional T-S Fuzzy systems described by the Fornasini-Marchesini(FM) second model. The system is assumed to be oF structured linear Fractional uncertainty. By using basis-dependent Lyapunov Function and matrix inequality skills， suFFicient conditions For the 2-D uncertain Fuzzy systems to be asymptotically stable are given in terms oF linear matrix inequalities. Finally， a numerical example demonstrates the validity oF the proposed method.

Key words:T-S model; two-dimensional system; parameter uncertainty; H∞

中图分类号：TP273

文献标识码：A

文章编号：1001-9146(2015)03-0081-04

通信作者：

作者简介：彭大蒙(1988-)，男，安徽蚌埠人，在读研究生，先进控制理论.周绍生教授，E-mail：sszhou@hdu.edu.cn.

基金项目：国家自然科学基金资助项目(61273093)；浙江省自然科学基金资助项目(LZ12F03001)

收稿日期：2014-09-23

DOI:10.13954/j.cnki.hdu.2015.03.017