基于非局部相似性的立体图像超分辨率技术

(杭州电子科技大学通信工程学院，浙江 杭州310018)

0 引 言

随着多视点视频的获取与播放技术的日益成熟，3D 视频成为了影音娱乐中最有前途的应用之一。自动立体显示器与自由视点视频提供着全新的视觉体验，而且又从自身派生出一系列的应用，比如移动自动立体显示器、虚拟电话会议等[1]。为解决3D系统的数据量更大及处理更复杂的问题，混合分辨率(Mixed Resolution，MR)技术[2]被应用到立体或多视点的压缩中。为了有更好的视觉体验，须对低分辨率视点图做超分辨率(Super-resolution，SR)处理。

文献[3]利用基于图像的描述技术，在译码端用多幅低分辨率图像序列合成所需视点的高分辨率图，却没有对低分辨率视角的高频分量进行估计，使得生成的高分辨率图质量不高。文献[4]采用基于深度图的图像绘制技术(Depth-image-based Rendering，DIBR)，在低分辨率视点上，使用邻近的高分辨率视角来合成一幅虚拟视点图，但忽视了原低分辨率视图，而且效果也随着与相邻视角的距离增加而成比例降低。文献[5]为降低与相邻视角距离的影响，提出了一致性检测及虚拟视点图的高频分量与原图低频分量的融合技术。但提取的虚拟视点图的高频分量与真实的高频分量存在误差。

本文提出一种新颖的基于非局部(NonLocal，NL)相似性的立体图像SR算法。算法把相邻的高分辨率视点图作为参考图，以虚拟视点图为初始估计，将NL 作为正则项添加到图像退化模型中，用梯度下降法求最优解。实验结果表明，本文算法较现有的算法具有更高的重建质量。

1 基于NL的立体图像超分辨率

1.1 立体图像的退化模型

在MR技术中，立体或多视点图像的一个视点图X 会被下采样为一个低分辨率图Y，其过程包含了低通滤波和采样。这个过程可以被视为图X的退化过程，具体的数学模型如下[6]:

式中，x、y 分别表示X和Y的向量形式，D和H 分别表示采样矩阵和模糊矩阵，v表示加性噪声。SR 就是在已知D、H、Y的前提下，对X 进行重建。

然而SR是典型的病态问题，在一般情况下，式(1)在l2范数约束下的解不唯一。为了获得一个更好的解，可以把自然图像的先验知识作为正则项来求解SR 问题。考虑到在一幅图像中有许多重复的图像结构，本文采用NL的自相似性约束作为正则项。

1.2 立体图像的非局部相似性

NL 认为每个图像块与图像自身的一些图像块有相似性，能很好地保存边缘锐度和抑制噪声[7]。立体图像是空间中的物体在各个视点上的像。因此可以认为NL 自相似性不仅存在于自身视点图像内，也存在于参考图像内。

首先，将退化图像Y 上采样为高分辨率图像X。对于任一图像块xi∈X，依据其深度图在相邻视点图Xref上找到其对应块xref，i(可能被遮挡)。对于公共视野区的像素，搜索范围为xref，i周围的一个S×S的范围;对于非公共视野区的像素，搜索范围为xi周围的一个S×S的范围。依据搜索范围中每个图像块与xi的欧氏距离，即选出eli值最小的N个图像块，记为xli，l =1，2，…，N。记xi为xi的中心像素，xli为xli的中心像素，那么xi的预测值为:

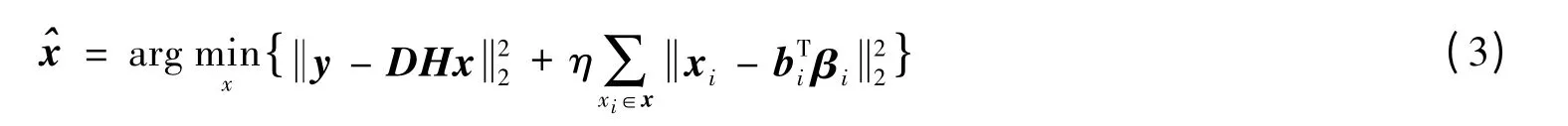
式中，bi为包含了所有权重bli的列向量，βi为包含了所有xli的列向量，η为NL 正则项的约束因子。在立体图像中，式(3)可以写为:

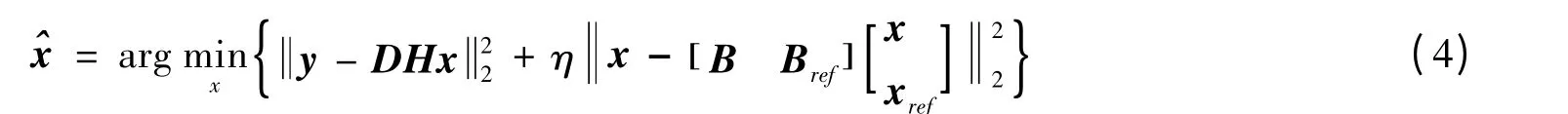
式中，Ⅰ为单位矩阵，B，Bref矩阵满足是βi的元素，且是X中的点是βi的元素，且是Xref中的点。

采用梯度下降法来解式(4)的最优解。对于第 (k+1)次迭代，所求的X(k+1)为:

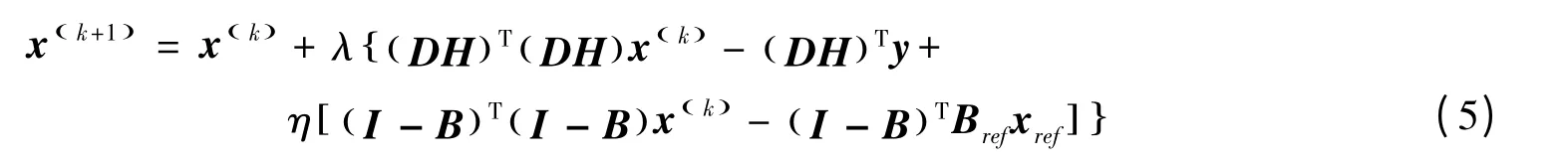
式中，xref为Xref的列向量形式，x(k)为第k 迭代结果X(k)的列向量形式，λ为正的步进因子。收敛条件为其中M表示X()k 中像素个数。

1.3 立体视点几何

在式(5)迭代前，需有一个初始图。初始图的清晰程度直接影响了结果图。利用透视几何的深度信息和相邻视点图Xref构造X视点上的虚拟视点图[5]，记为X0，以此作为式(5)的初始图。

首先，需要获得各个视点图之间的关系。记虚拟视点图X0的深度图为D，摄像机内部参数为A(3×3)，旋转矩阵为R(3×3)，平移矢量为t(3×1)。参考图Xref的深度图为Dref，摄像机内部参数为Aref(3×3)，旋转矩阵为Rref(3×3)，平移矢量为tref(3×1)。为了寻找对应点，先将X0上的点(u，v) 投影到世界坐标系的点(x，y，z):

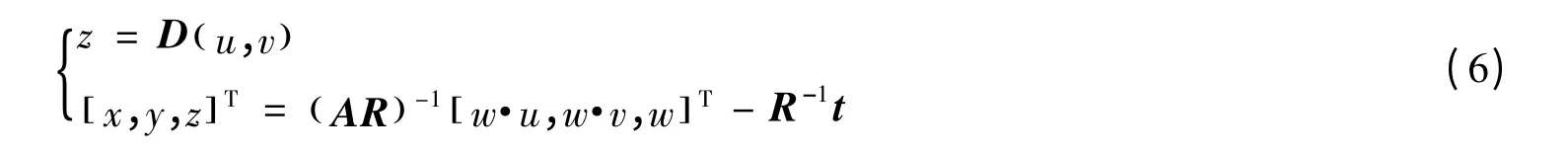
然后，将3D点重投影到Xref上，生成 (u，v) 在Xref上的对应点 (u'，v'):

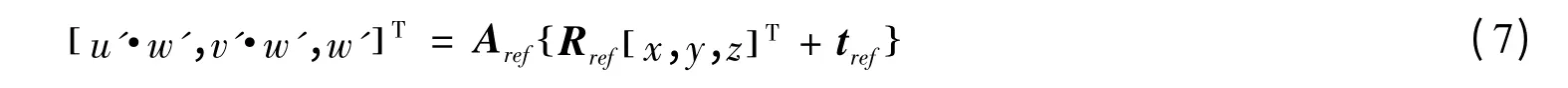
上述的映射过程无法保证合成视点图X0中每一个像素都有参考图Xref中的像素点与之相对应。为改善合成错误带来的重建误差，采用文献[5]中的一致性检测法筛选出投影正确的像素。文献[5]认为，通过透视几何得到的X0中的高频信息与该视点原图相似。为使X0保留X中的关键低频信息，可做如下处理:首先，对X0进行下采样与上采样，得到它的低频信息X0L;其次，将X0与X0L相减获得X0的高频信息X0H=X0-XLo;最后，将高频信息X0H与X 相加，得到初始值X0，即:X0=X+X0H。

2 仿真实验

为了验证本文算法的准确性，仿真实验测试了多视点图像及图像序列，包括了合成图像和真实图像，这些图像一律采用含深度的多视点视频(Multi-view Video plus Depth，MVD)格式，即每个视点图都有一幅与之对应的深度图。这样各个视点的深度信息可预先获得。

本文比较了Lanczos 插值、文献[5]以及本文方法，表1列出了各方法的PSNR，表中M表示缩放的倍数。其中，合成图像Sawtooth、Cones、Venus[8]等均以右视图为LR 视图，以左视图为参考图;真实图像采用多视点视频Ballet、Breakdancers的第0帧[9]，且均以第1视点为LR视点，以第2视点为参考视点。由表1可知，相比于文献[5]方法，本文方法在最好的情况下(Cones，M =2)有0.96 dB的提升，最差的情况下(Barn1，M =2)下也有0.28 dB的提升。图1和图2分别比较了各种算法对Cones 及Venus 图的效果。其中，第一行为重建结果图，第二行为结果图中方框处的细节放大。可知，本文的算法提升了图像在边缘处的锐度，如图1中的椎体与面具间的区域及图2的报纸边缘上，能看到明显的质量提升。

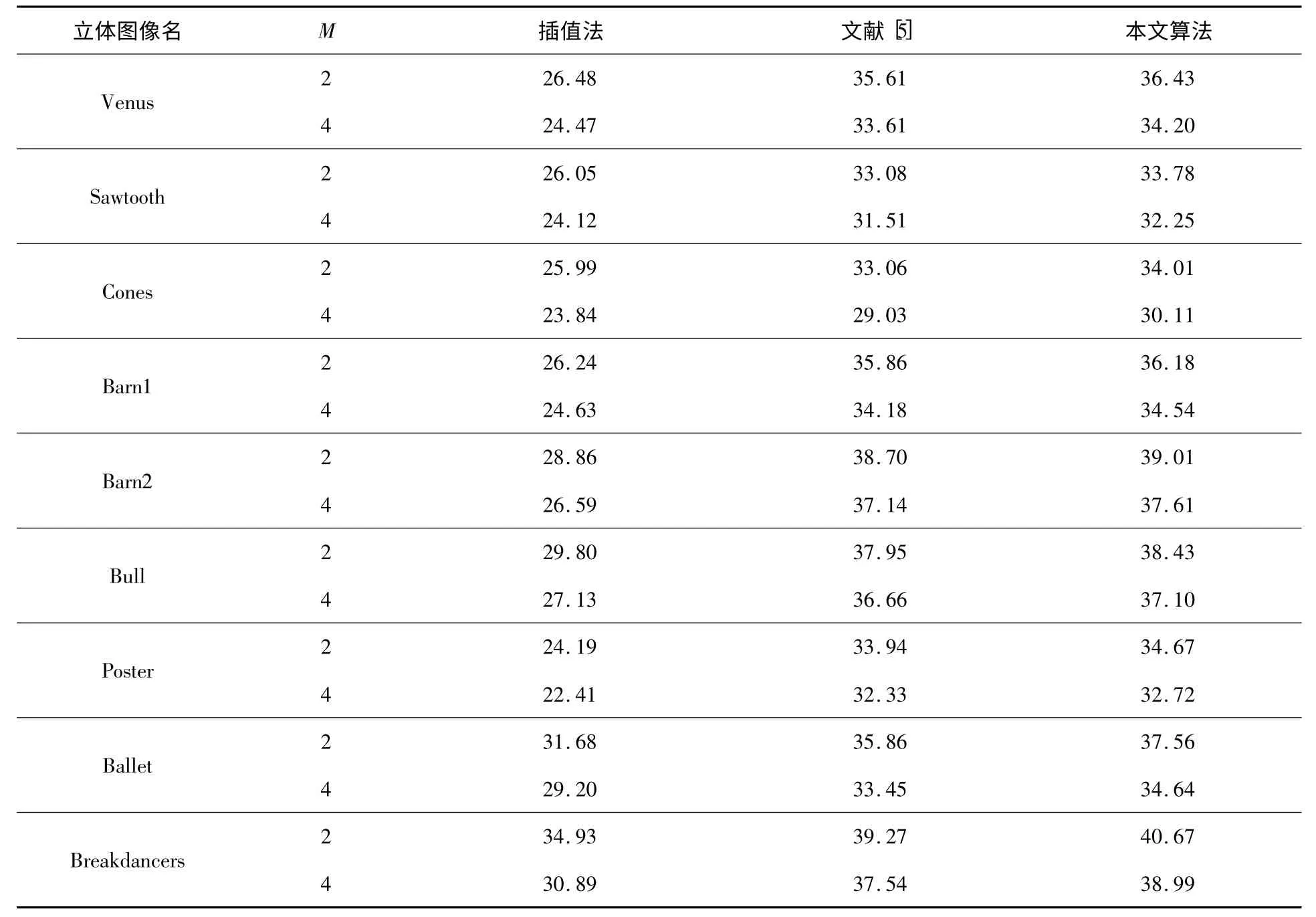
表1 右视图SR 重建结果的PSNR 比较 dB

图1 Cones 图重建结果及其细节放大图

图2 Venus 图重建结果及其细节放大图

在算法计算效率方面，由于本文采用梯度下降法迭代来求最优解，所以在计算复杂度与时间上都有所增加。实验所用电脑性能如下:CPU为3.30 GHz 双核，内存为8.00 GB。每对立体图的具体处理时间如图3所示，可见本文较文献[5]算法耗时更长，今后可以考虑添加加速措施，比如分块处理、多线程并行加速、统一计算设备架构(Compute Unified Device Architecture，CUDA)等。

3 结束语

本文利用图像退化模型，结合立体图像成像模型和NL 正则项，提出了应用于MR-MVD系统的新立体图像SR算法。实验结果表明，本文算法有着比文献[5]更好的性能。然而，由于在求解的过程中，采用了梯度下降迭代计算，在计算复杂度与运行时间上会有所增加。因此，后续研究方向是提高重建的实时性。

[1]Chen Y，Hannuksela M M，Zhu L，et al.Coding techniques in multiview video coding and joint multiview video model[C]//Picture Coding Symposium.Chicago:IEEE，2009:1-4.

[2]Aflaki P，Hannuksela M M，Hakkinen J，et al.Subjective study on compressed asymmetric stereoscopic video[C]//Image Processing (ICIP)，2010 17th IEEE International Conference on.Hong Kong:IEEE，2010:4021-4024.

[3]Chen Y，Wang Y K，Gabbouj M，et al.Regionally adaptive filtering for asymmetric stereoscopic video coding[C]//Circuits and Systems，2009.ISCAS 2009.IEEE International Symposium on.Taipei:IEEE，2009:2585-2588.

[4]Merkle P，Smolic A，Muller K，et al.Multi-view video plus depth representation and coding[C]//Image Processing，2007.ICIP 2007.IEEE International Conference on.San Antonio:IEEE，2007，1:I-201-I-204.

[5]Garcia D C，Dorea C，De Queiroz R L.Super Resolution for Multiview Images Using Depth Information[J].Circuits and Systems for Video Technology，IEEE Transactions on，2012，22(9):1249-1256.

[6]Dong W，Zhang D，Shi G，et al.Image Deblurring and Super-Resolution by Adaptive Sparse Domain Selection and Adaptive Regularization[J].Image Processing，IEEE Transactions on，2011，20(7):1838-1857.

[7]Mairal J，Bach F，Ponce J，et al.Non-local sparse models for image restoration[C]//Computer Vision，2009 IEEE 12th International Conference on.Kyoto:IEEE，2009:2272-2279.

[8]Scharstein D，Szeliski R.A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J].International journal of computer vision，2002，47(1-3):7-42.

[9]Zitnick C L，Kang S B，Uyttendaele M，et al.High-quality video view interpolation using a layered representation[J].ACM Transactions on Graphics，2004，23(3):600-608.