超声悬浮过程中圆柱体的旋转运动机理研究∗
2017-08-07秦修培耿德路洪振宇魏炳波
秦修培 耿德路 洪振宇 魏炳波
(西北工业大学应用物理系,西安 710072)
超声悬浮过程中圆柱体的旋转运动机理研究∗
秦修培 耿德路 洪振宇 魏炳波†
(西北工业大学应用物理系,西安 710072)
(2017年1月21日收到;2017年4月10日收到修改稿)
研究了圆柱体在超声悬浮过程中的旋转运动机理.实验发现:悬浮圆柱体的密度和长径比越小,转动惯量越小,其稳态旋转的转速越大;反射端在水平方向的偏移会产生回复力矩,使圆柱体停止旋转,且圆柱体静止时的轴线方向与反射端偏移方向垂直;在圆柱体两端加入适当的外界干扰可以主动抑制其旋转.计算表明,悬浮圆柱体的旋转起源于其质心偏移产生的力矩,而反射端位置的偏移以及发射端的倾斜均会抑制圆柱体的旋转.
超声悬浮,有限元方法,圆柱体,旋转
1 引 言
超声悬浮是一种重要的无容器处理技术[1,2],其原理是利用强声场的非线性效应产生的声辐射力抵消重力以实现物体的悬浮,可以避免样品与其他物体的接触,有效地满足某些科学研究过程中对无容器、超洁净环境的需求,已在分析化学[3,4]、生物医学[5,6]、材料加工制备[7,8]以及液滴动力学[9−11]等方面得到了广泛应用.近年来,超声悬浮条件下物体的动力学过程引起了研究者们的广泛兴趣,在超声悬浮实验过程中可以观察到悬浮物体的振荡[12,13]和旋转运动.其中,悬浮物体的振荡和稳定性问题已经在实验以及计算方面得到了较为系统的研究[14−17],然而关于其旋转运动的机理却鲜有报道,这种悬浮不稳定性给实验过程中样品的定位和探测带来困难,甚至导致实验失败.因此,探索超声悬浮条件下物体旋转运动的机理并实现对其旋转的主动控制具有重要意义.
实验系统的非严格轴对称性、悬浮物体的振荡以及声流[18]均有可能成为样品旋转的原因,但是实验上很难对这些因素一一进行分析.随着计算科学领域的发展,仿真模拟提供了一种有效的手段.与其他方法相比,有限元法可以将复杂的几何体简化,并且不考虑整个定义域的复杂边界条件,已在声学模拟方面得到了广泛应用[19−21].本文首先对不同材料的圆柱体在超声悬浮过程中的转速进行实验测定,提出了三种可能产生合力矩的原因;然后应用有限元法建立模型,对其进行模拟和分析,探讨了不同条件下圆柱体在旋转过程中的受力情况,并进行了相关的实验验证;最后提出了一种主动抑制旋转的便捷途径.
2 实验技术与模拟方法
2.1 超声悬浮实验
圆柱体旋转运动机理的实验研究在单轴式超声悬浮装置上进行,该装置主要包括超声电源、压电陶瓷换能器、发射端和反射端,如图1(a)所示,超声波的频率为22 kHz.调节发射端与反射端的间距,使装置达到三个波节的谐振状态,将聚甲基丙烯酸甲酯(polymethylmethacrylate,PMMA)有机玻璃棒、铝棒和铁棒分别置于中间波节的悬浮位置进行实验,圆柱棒悬浮时轴线沿水平方向,转轴沿竖直方向且通过其质心.实验过程中采用Nikon BM-5相机拍摄圆柱体的运动状态,采用MONARCH ACT-3X型转速表测定圆柱体的转速.
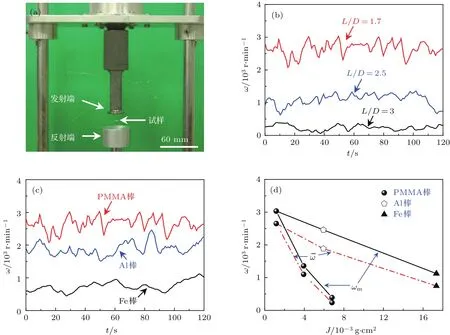
图1 (网刊彩色)超声悬浮状态下Φ3 mm圆柱体的旋转运动规律 (a)超声悬浮装置图;(b)不同长径比的PMMA圆柱体转速随时间的变化;(c)不同材料的圆柱体转速随时间的变化;(d)圆柱体转速与转动惯量的关系Fig.1.(color online)Rotation characteristics of ultrasonically levitated cylinder with 3 mm diameter:(a)Experimental setup for ultrasonic levitation;(b)rotation speeds of the PMMA cylinders with di ff erent length-to-diameter ratios;(c)rotation speeds of the cylinders with di ff erent materials;(d)rotation speeds of the cylinders versus rotational inertia.
2.2 数值模拟方法
本文采用基于有限元法的COMSOL Multiphysics 5.2a仿真模拟软件,利用压力声学模块建立模型,进而对圆柱体的旋转运动机理进行模拟研究.模型如图2所示,图2(a)为整体的三维模型示意图,图2(b)为通过圆柱体轴线的x-z截面上的模型示意图.其中,发射端的半径为12.5 mm,反射端的半径为20 mm,曲率半径为40 mm,圆柱体长度为5 mm,底面半径为1.5 mm,且其轴线与z轴垂直,圆柱体的边界设置为硬声场边界,计算中所使用的声波在空气中的传播速度c0为340 m/s,空气的密度ρ0为1.21 kg/m3,忽略媒质气体的黏滞性.利用此模型可以直接得出求解域中各点的声压p和流体质点速度u.
圆柱体旋转时转轴l通过圆柱体的质心且平行于z轴,对于圆柱体表面上任意一点A,该点处有一面元dS,那么作用在该面元上的声辐射力dF可表示为[22]

圆柱体在此处受到的关于转轴l的力矩dM可以表示为
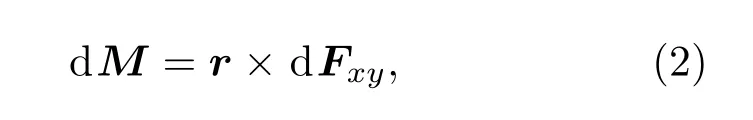
其中r为点A到转轴l的距离矢量,dFxy为dF在x-y平面内的分量,对dM在整个圆柱体表面进行积分就可以得到总的关于转轴l的合力矩M,计算过程中规定逆时针为旋转正方向.另外,根据Gor’kov的理论[23],在理想流体中,可以定义一个与悬浮样品无关的声辐射力的时间平均势

已知声压p和流体质点速度u可以直接计算得到˜U,利用上述模型可以研究圆柱体在超声悬浮过程中的旋转运动机理.

图2 (网刊彩色)数值计算模型示意图 (a)三维图;(b)截面图Fig.2.(color online)Schematic of numerical simulation model:(a)Three-dimensional diagram;(b)sectional diagram.
3 结果与讨论
3.1 超声悬浮状态下圆柱体旋转规律
直径D为3 mm的圆柱体被置于悬浮节点之后开始加速旋转,由于受到空气阻力的作用,其转速在一段时间之后趋于稳定,稳定后的旋转方向由初始旋转方向决定,此时对其转速进行测定,结果如图1(b)和图1(c)所示.图1(b)给出了不同长度L的PMMA有机玻璃棒转速随时间的变化,结合图1(d),可以看出圆柱体长径比L/D越大,转动惯量越大,转速越低.图1(c)给出了长度为5 mm的不同材料的圆柱体转速随时间的变化,密度最小的PMMA棒转速较高,而密度最大的Fe棒转速相对较低.这是因为三种圆柱体的形状和尺寸均相同,受到的声辐射力和空气阻力相似,在相同的实验条件下,转动惯量越大,其转速越低,如图1(d)所示,其中¯ω和ωm分别代表圆柱体的平均转速和最大转速.从图1(d)还可以看出,由于不同材料且不同长径比的圆柱体与空气的摩擦阻力矩各不相同,其转速与转动惯量的关系并非是单调的.
圆柱体旋转的根本原因是其所受到的合力矩不为零.在理想的实验环境中,整个体系关于悬浮圆柱体的轴线是对称的,在这种情况下,圆柱体轴线两侧的声压分布是对称的,声辐射力在圆柱体上产生的合力矩为零.而在实际的实验过程中,悬浮圆柱体的振荡以及发射端与反射端相对位置的微小变化都会破坏整个声场分布的对称性,进而影响圆柱体的运动状态.基于以上分析,本文从以下三方面来探讨悬浮圆柱体合力矩不为零的原因.
3.2 旋转运动起源于圆柱体质心偏移
首先我们讨论悬浮圆柱体质心偏移对其所受合力矩的影响,对模型进行如下设定:发射端与反射端同轴,悬浮圆柱体的质心沿着y轴正方向偏移1 mm,沿着x轴正方向从0 mm逐渐偏移到1 mm,计算结果如图3所示.
未放置圆柱体时,时间平均势关于发射端与反射端的轴线对称分布,如图3(a)所示.将圆柱体放置于中间的悬浮节点,并使其质心沿着x轴和y轴正方向均偏移1 mm,重新计算总声压场的分布,如图3(b)所示,可以很明显地看出,通过圆柱体轴线的x-y截面上的声压已不再对称分布.图3(c)为圆柱体质心沿着y轴正方向偏移1 mm,沿着x轴正方向从0 mm逐渐偏移到1 mm时所受到的合力矩的变化,随着偏移程度的增大,圆柱体受到的合力矩逐渐增大,这说明圆柱体质心位置的偏移会产生一个驱动其旋转的合力矩.
3.3 反射端偏移抑制旋转运动
由于实验装置存在系统误差,发射端与反射端有可能不同轴,在这种情况下,悬浮圆柱体的受力同样会发生变化.基于此,对模型进行如下设定:发射端与反射端相互平行,且反射端的轴线相对发射端向x轴正方向分别偏移δx=1,2和3 mm.
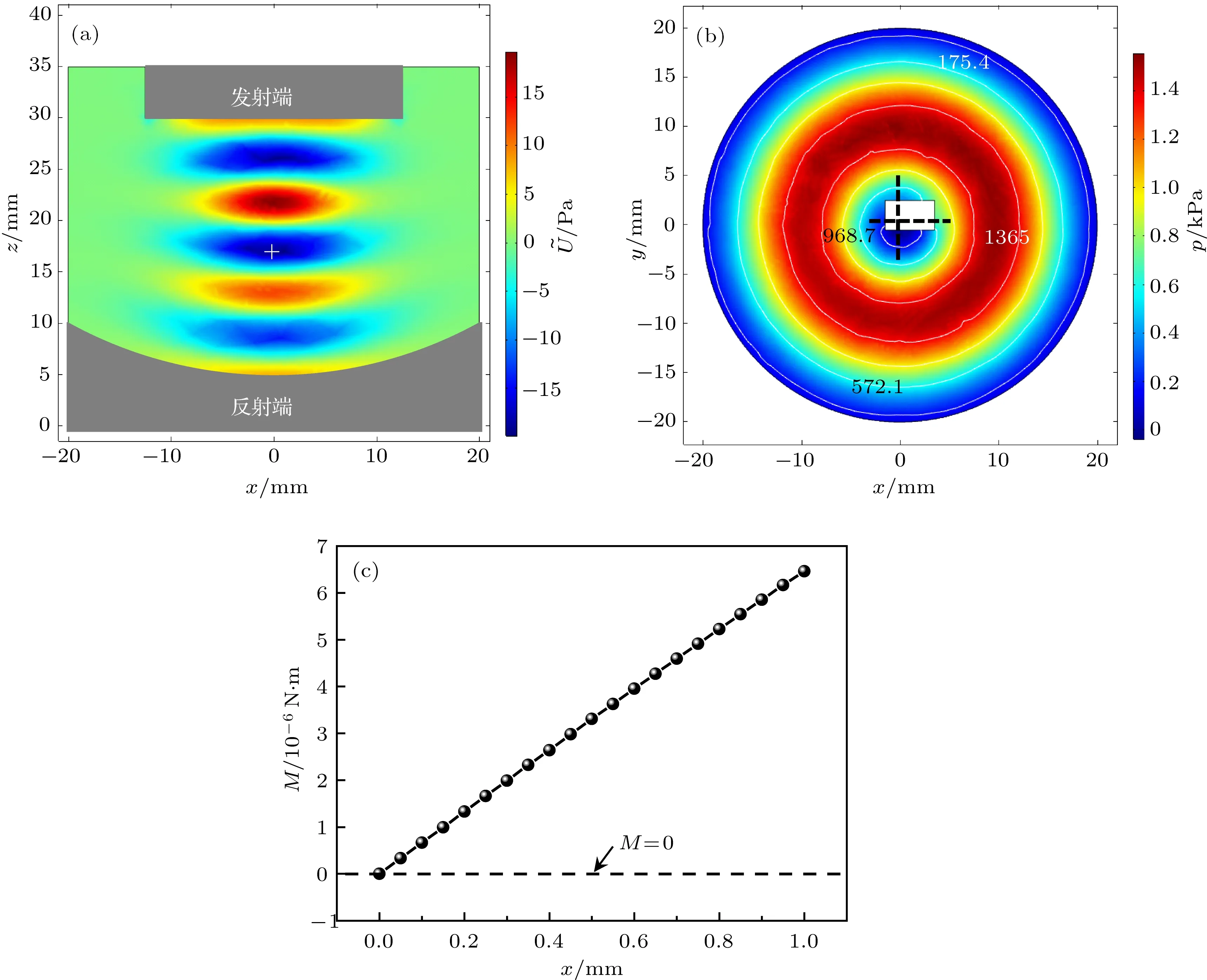
图3 (网刊彩色)悬浮圆柱体质心偏移时的声场分布及其受力情况 (a)未放置圆柱体时的时间平均势分布;(b)声压在通过圆柱体轴线的x-y截面上的分布;(c)圆柱体在不同位置受到的力矩Fig.3.(color online)Distribution of acoustic pressure fi eld and force situation around a levitated cylinder with mass center deviation:(a)Distribution of the time-average potential without cylinder;(b)distribution of acoustic pressure fi eld in the x-y section across the cylinder axis;(c)torque acting on the cylinder in di ff erent positions.
反射端偏移时,悬浮节点的位置也会发生偏移,如图4(a)所示.将圆柱体放置于中间的悬浮节点,并使其轴线与x轴正方向的夹角φ从−π/2逐渐变化到π,重新计算声场分布.图4(b)给出了当圆柱体的轴线与x轴正方向的夹角为π/6时,总声压场在通过圆柱体轴线的x-y截面上的分布图,可以很直观地看出圆柱体轴线两侧的声压场分布明显不同,那么它此时受到的合力矩有可能不为零.
图4(c)给出了当反射端偏移的程度不同时,圆柱体在不同位置所受到的力矩.从图4(c)可以看出:夹角φ为零即圆柱体的轴线与x轴平行时,合力矩M=0,而且此时若φ有微小的变化,圆柱体在合力矩的作用下会偏离平衡位置,表明此时圆柱体处于一个不稳定的平衡状态;夹角φ为π/2即圆柱体的轴线与x轴垂直时,合力矩M=0,与φ=0时不同,此刻若φ有微小的变化,圆柱体在合力矩的作用下会回复到平衡位置,此时圆柱体处于一个稳定的平衡状态.从图4(c)还可以得出,当圆柱体处于稳定的平衡状态时,反射端的偏移程度越大,圆柱体偏离平衡状态后受到的回复力矩越大,即越难以转动.
以直径为3 mm、长度为5 mm的PMMA圆柱体为例,平移反射端进行超声悬浮实验.图5给出了三种不同条件下悬浮圆柱体的运动状态.图5(a)表示反射端与发射端同轴时圆柱体处于旋转运动状态.一旦反射端发生偏移,圆柱体的运动状态随之改变,如图5(b)和图5(c)所示,当反射端沿着不同方向偏移3 mm时,圆柱体最终处于静止状态,图中虚线箭头方向代表反射端的偏移方向.可以看出,圆柱体静止时,其轴线与反射端的平移方向相互垂直,这说明图4(c)的计算结果是合理的.

图4 (网刊彩色)反射端位置偏移时的声场分布和悬浮圆柱体的受力情况 (a)未放置圆柱体时的时间平均势分布;(b)声压在通过圆柱体轴线的x-y截面上的分布;(c)圆柱体在不同位置受到的力矩Fig.4.(color online)Distribution of acoustic pressure fi eld and force situation around a levitated cylinder with a deviating re fl ector:(a)Distribution of the time-average potential without cylinder;(b)distribution of acoustic pressure fi eld in the x-y section across the cylinder axis;(c)torque acting on the cylinder in di ff erent positions.

图5 (网刊彩色)反射端位置偏移时圆柱体的运动状态 (a)未发生偏移;(b),(c)沿着箭头方向偏移3 mmFig.5.(color online)Motion state of cylinder as the re fl ector deviates:(a)Not deviate;(b)and(c)deviate along the arrow direction with 3 mm.
3.4 发射端倾斜抑制旋转运动
发射端与反射端不同轴的情况还有另外一种即发射端与反射端的端面相互不平行,为了研究在此条件下悬浮圆柱体的受力情况,对模型进行如下设定:反射端位置不变,仅改变发射端的倾斜角ψ,即其端面与x-y平面的夹角,ψ分别取π/180,π/90和π/60,计算结果如图6所示.我们将图6(a)和(b)与图4(a)和(b)相比较可以看出,这两种情况下悬浮节点位置均会发生偏移,且放置圆柱体之后,其轴线两侧的声压场分布也不对称.根据3.3节的讨论,可以推测此时圆柱体受到的合力矩也不为零.
图6(c)给出了当发射端倾斜程度不同时,圆柱体在不同位置所受到的力矩.与图4(c)相比,二者的变化规律类似,都存在两种合力矩为零的情况.当φ=0,即圆柱体轴线与发射端轴线和反射端轴线处于同一平面内时,圆柱体处于不稳定的平衡状态;φ=π/2,即圆柱体轴线与发射端轴线和反射端轴线确定的平面垂直时,圆柱体处于稳定的平衡状态.同样以PMMA圆柱体为例进行了实验验证,但是圆柱体最终未能静止在稳定的平衡状态,这可能是由于发射端倾斜时,圆柱体受到的合力矩较小,数量级在10−9N·m,与3.2节和3.3节两种情况中的10−6N·m相比,差距很大.而在实际的实验过程中,圆柱体的质心不可避免地会偏离势阱位置,由此在圆柱体上产生的合力矩远大于发射端倾斜时所产生的合力矩,这将对图6(c)的实验验证造成很大的影响.但是从图4(c)和图6(c)可以看出,两种情况下圆柱体受到的合力矩的变化趋势是一致的,根据3.3中的实验验证,我们有理由预测在没有其他因素的干扰下,仅改变发射端倾斜角时,圆柱体最终会静止在稳定的平衡状态.
3.5 主动抑制圆柱体旋转的便捷途径
以上讨论了圆柱体所受合力矩不为零的三种可能,那么如何在发射端与反射端同轴且圆柱体质心不发生偏移的情况下主动抑制圆柱体的旋转?根据前面的讨论,声场的分布对悬浮圆柱体所受到的合力矩有着重要影响.在实验过程中可以人为地引入外界物体来改变声场的分布,基于此,设计了如下实验:调节反射端的位置,使其与发射端同轴,在悬浮圆柱体的两端对称地放置两个陶瓷圆柱体,陶瓷圆柱体轴线与x轴平行,这种情况下圆柱体将不再旋转,而是最终处于静止状态,并且与两个陶瓷圆柱体同轴,如图7(a)所示.

图7 (网刊彩色)施加外界干扰对悬浮圆柱体旋转的影响 (a)圆柱体的运动状态;(b)圆柱体在不同位置受到的力矩Fig.7.(color online)E ff ect of external disturbance on the rotation state of levitated cylinder:(a)Motion state of cylinder;(b)torque acting on the cylinder in di ff erent positions.
为了对上述实验现象进行分析,利用有限元法进行了模拟.图7(b)给出了圆柱体与x轴正方向的夹角φ从−π/2逐渐变化到π时,其所受到的合力矩的变化趋势.与图4(c)和图6(c)相比,图7(b)中也存在两种合力矩为零的情况,不同的是,圆柱体在φ=0时处于稳定的平衡状态,而在φ=π/2时处于不稳定的平衡状态,这与上述实验现象是符合的.
4 结 论
本文研究了超声悬浮过程中圆柱体的旋转运动机理,所得结论如下.
1)实验发现,超声悬浮过程中圆柱体的旋转速度与其密度和长径比有关,密度和长径比越小,转动惯量越小,其稳态旋转的转速越大.计算表明,圆柱体质心位置的偏移会产生驱动其旋转的合力矩,且偏移程度越大,所受到的合力矩越大.
2)发射端与反射端之间不同轴会在圆柱体上产生合力矩.计算和实验发现,若对反射端进行平移,圆柱体最终会静止在稳定的平衡位置,且其静止时的轴线方向与反射端平移方向垂直.与反射端平移相比,发射端倾斜产生的合力矩较弱,在其作用下同样会使圆柱体最终静止在稳定的平衡位置,且圆柱体轴线与发射端轴线和反射端轴线确定的平面垂直.
3)在悬浮圆柱体两端对称的放置两个位置固定的圆柱体进行干扰,可以抑制其旋转,圆柱体最终静止在平衡位置,并且与两个干扰圆柱体同轴.利用有限元方法进行了模拟,模拟结果与实验现象相符合.
感谢吴宇昊和杨尚京等同事在实验和分析过程中给予的有益帮助.
[1]Brandt E H 2001 Nature 413 474
[2]Xie W J,Cao C D,Wei B B 1999 Acta Phys.Sin.48 250(in Chinese)[解文军,曹崇德,魏炳波 1999物理学报48 250]
[3]Brotton S J,Kaiser R I 2013 Rev.Sci.Instrum.84 055114
[4]Chainani E T,Ngo K T,Scheeline A 2013 Anal.Chem.85 2500
[5]Benmore C J,Weber J K R 2011 Phys.Rev.X 1 011004
[6]Puskar L,Tuckermann R,Frosch T,Popp J,Ly V,Mc-Naughton D,Wood B R 2007 Lab Chip 7 1125
[7]Radnik J,Bentrup U,Leiterer J,Brückner A,Emmerling F 2011 Chem.Mater.23 5425
[8]Wolf S E,Leiterer J,Kappl M,Emmerling F,Tremel W 2008 J.Am.Chem.Soc.130 12342
[9]Yan Z L,Xie W J,Shen C L,Wei B B 2011 Acta Phys.Sin.60 064302(in Chinese)[鄢振麟,解文军,沈昌乐,魏炳波2011物理学报60 064302]
[10]Saha A,Basu S,Suryanarayana C,Kumar R 2010 Int.J.Heat Mass Transfer 53 5663
[11]Shao X P,Xie W J 2012 Acta Phys.Sin.61 134302(in Chinese)[邵学鹏,解文军 2012物理学报 61 134302]
[12]Rudnick J,Barmatz M 1990 J.Acoust.Soc.Am.87 81
[13]Baer S,Andrade M A B,Esen C,Adamowski J C,Schweiger G,Ostendorf A 2011 Rev.Sci.Instrum.82 105111
[14]Barrios G,Rechtman R 2008 J.Fluid Mech.596 191
[15]Foresti D,Nabavi M,Poulikakos D 2012 J.Fluid Mech.709 581
[16]Pérez N,Andrade M A B,Canetti R,Adamowski J C 2014 J.Appl.Phys.116 184903
[17]Andrade M A B,Pérez N,Adamowski J C 2014 J.Acoust.Soc.Am.136 1518
[18]Trinh E H,Robey J L 1994 Phys.Fluids 6 3567
[19]Hong Z Y,Lü P,Geng D L,Zhai W,Yan N,Wei B 2014 Rev.Sci.Instrum.85 104904
[20]Andrade M A B,Bernassau A L,Adamowski J C 2016 Appl.Phys.Lett.109 044101
[21]Hong Z Y,Zhang J,Drinkwater B W 2015 Phys.Rev.Lett.114 214301
[22]Lee C P,Wang T G 1993 J.Acoust.Soc.Am.94 1099
[23]Gor’kov L P 1962 Sov.Phys.Dokl.6 773
PACS:43.25.Uv,43.25.Qp,47.11.Fg,06.30.GvDOI:10.7498/aps.66.124301
Rotation mechanism of ultrasonically levitated cylinders∗
Qin Xiu-PeiGeng De-Lu Hong Zhen-Yu Wei Bing-Bo†
(Department of Applied Physics,Northwestern Polytechnical University,Xi’an 710072,China)
21 January 2017;revised manuscript
10 April 2017)
The rotation of levitated object in the ultrasonic levitation experiment is a common phenomenon.This instability may give rise to many difficulties in locating and detecting the levitated object and even cause the experiment to fail.However,the relevant research of the rotation mechanism of levitated object is seldom carried out.In this work,the rotation mechanism of cylinder in a single-axis ultrasonic levitator is investigated experimentally and theoretically.In the ultrasonic levitation experiment,the cylinder begins to rotate about an axis along the vertical direction as it is levitated at the node between the emitter and re fl ector.The rotation speed of cylinder tends to a stable value due to the e ff ect of the air resistance,and the fi nal rotation direction is determined by its initial rotation state.Experimental results demonstrate that the rotation speed increases with the decreases of density and length-to-diameter ratio of the cylinder.In order to analyze the rotation mechanism,the fi nite element method is used to calculate the distribution of acoustic pressure fi eld and the torque acting on the cylinder for each of three di ff erent cases.Numerical results reveal that the position o ff sets of the cylinder and the re fl ector as well as the tilt of the emitter can all result in the nonaxisymmetrical distribution of acoustic pressure fi eld.Hence,a nonzero torque acting on the cylinder may be generated and the rotation state of the levitated cylinder is subsequently a ff ected.The position o ff set of the cylinder can produce a torque driving itself to rotate and the torque increases with the increase of the deviation degree.A restoring torque suppressing the rotation of cylinder can be generated by deviating the re fl ector from the horizontal direction.The cylinder eventually keeps stationary state with its axis perpendicular to the o ff set direction of the re fl ector,showing good accordance with the experimental results.In addition,it is predicted that tilting the emitter can also o ff er a restoring torque which makes cylinder eventually static with its axis perpendicular to the plane through the axes of the emitter and the re fl ector.However,this restoring torque is approximately three orders of magnitude smaller than that generated by deviating the re fl ector.In the end,both experimental results and numerical simulations show that the rotation of the cylinder can be e ff ectively suppressed under the disturbance of two fi xed cylinders when the emitter and the re fl ector are coaxial.The cylinder eventually stays still and keeps coaxial with the two fi xed cylinders.
ultrasonic levitation, fi nite element method,cylinder,rotation
10.7498/aps.66.124301
∗国家自然科学基金(批准号:51327901,51501153)资助的课题.
†通信作者.E-mail:bbwei@nwpu.edu.cn
©2017中国物理学会Chinese Physical Society http://wulixb.iphy.ac.cn
*Project supported by the National Natural Science Foundation of China(Grant Nos.51327901,51501153).
†Corresponding author.E-mail:bbwei@nwpu.edu.cn
