含集中参数弹性梁振动特性解析与实验识别*

2015-01-12王壮,洪明,许俊臣等

振动、测试与诊断 2015年4期

王壮1，2，洪明2，许俊臣2，崔洪宇2

（1.中国舰船研究设计中心武汉，430064）（2.大连理工大学船舶工程学院大连，116024）

基于Laplace变换推导出含集中质量与集中刚度弹性梁的振型函数和典型边界条件对应的频率方程，针对有一个集中质量与一个集中刚度的悬臂梁，求解出其固有特性，并利用基于自然激励技术（natural excitation technique，简称NEx T）的特征系统实现算法（eigensystem realization algorithm，简称ERA），即NEx T-ERA法对相应结构系统进行了模态识别。通过对比解析结果和实验结果，分别讨论了集中质量与集中刚度大小变化和位置变化时对梁振动特性的影响，得出了集中质量和集中刚度在悬臂梁上位置和大小变化时，悬臂梁固有频率的相应变化规律，为工程中具有集中质量和集中刚度等直弹性梁的振动分析方法和集中参数布置设计提供了参考。

弹性梁；集中质量；集中刚度；自然激励技术的特征系统实现算法（NEx T-ERA）；模态识别

引言

工程中一些结构可以简化成具有集中质量和集中刚度的等直弹性梁，设计中布置集中质量和集中刚度，追求优良的振动特性是非常有意义的。

具有集中质量与集中刚度的弹性梁的固有振动特性引起了国内外学者的研究兴趣［1-2］。Rossit等［3］用解析法推导出了悬臂梁自由端含有一个弹性支撑质量情况下的频率方程。Banerjee［4］采用动刚度法分析了相同问题。Chang［5］考虑了集中质量转动惯性的影响，分析了含有一个集中质量简支梁的振动特性。Low［6］采用特征分析法和Rayleigh法对比分析了仅含有集中质量的欧拉梁的固有频率。对同样的模型，Low［7］用Laplace变换的方法推导出了频率方程，并编写了计算程序。夏季等［8］采用Laplace变换推导出同时含有任意多个集中质量和集中刚度的弹性梁的振动特性的解析表达式，但表达式较为复杂，只适用于计算含有少量集中参数的情况。彭献等［9］在Low的基础上采用符号运算，推导出了便于计算的频率方程解析表达式，可计算含有集中质量较多情况下的频率方程，但未考虑含有集中刚度的情况。Wu等［10］采用解析和数值分析相结合的方法求出了含有任意集中质量和集中刚度的欧拉梁的固有频率和振型。Li等［11］用Ritz法求解了梁两自由端含有集中质量和弹性支撑的柔性梁的固有特性。以上研究只针对固有特性的求解，没有探讨集中质量和集中刚度大小或者位置布放对梁振动特性的影响，而这个研究认识对指导工程中相应结构减振是非常有必要的。

笔者基于Laplace变换的方法，针对典型边界条件，推导了含有任意集中质量与集中刚度的弹性梁弯曲振动的固有频率及振型的解析表达式。采用NEx T-ERA法［12］对含有集中参数的梁结构进行了模态识别实验，理论解析结果和实验结果吻合较好。利用验证的理论算法系统地讨论了集中质量和集中刚度的大小以及它们在梁上位置的改变对悬臂梁固有特性的影响，为工程中具有集中质量和集中刚度的等直梁提供了振动分析方法。

1 振型函数及频率方程推导

对于均匀等直弹性梁，其结构质量与刚度分布是均匀连续的。如果梁上含有集中质量与集中刚度，那么其系统质量与刚度在某一点会产生集中突变，此时可利用δ函数来描述集中质量与集中刚度对均匀梁的振动微分方程的影响，由于方程中δ函数的存在，求解将变得复杂。

1.1 采用δ函数描述集中质量与刚度的梁固有振型函数推导

图1所示为含有r个集中质量和s个线弹簧的

等直弹性梁，其自由振动微分方程为

图1 含集中质量与集中刚度弹性梁示意图Fig.1 Elastic beam with lumped masses and springs

其中：前两项为均匀直梁的弹性与惯性项；后两项为集中质量和集中刚度的影响项。

设解为w（x¯，t）=Y（x）sinωt，采用无量纲形

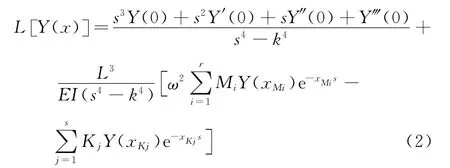
对式（2）作拉普拉斯逆变换，得到振型函数表达式为

其中：

其中：H（x）为单位阶跃函数。

为推导简便，作如下形式的符号代换，令式（3）中

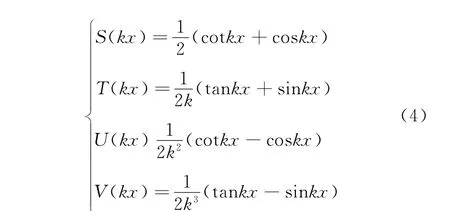
则满足以下导数关系

1.2 集中质量和弹簧在梁中位置时梁的频率方程

为得到频率方程，考虑梁上含有一个集中质量和一个集中刚度并位于梁中的简单情况，即式（6）中r=1，s=1，xM1=0.5和xK1=0.5，下面分别推导悬臂梁和简支梁振动的频率方程。

悬臂梁的边界条件为Y（0）=Y＇（0）=0，Y″（1）=Y‴（1）=0，将xM1和xK1分别代入振型函数式（6）的对应阶导函数式，令x=1，整理可得

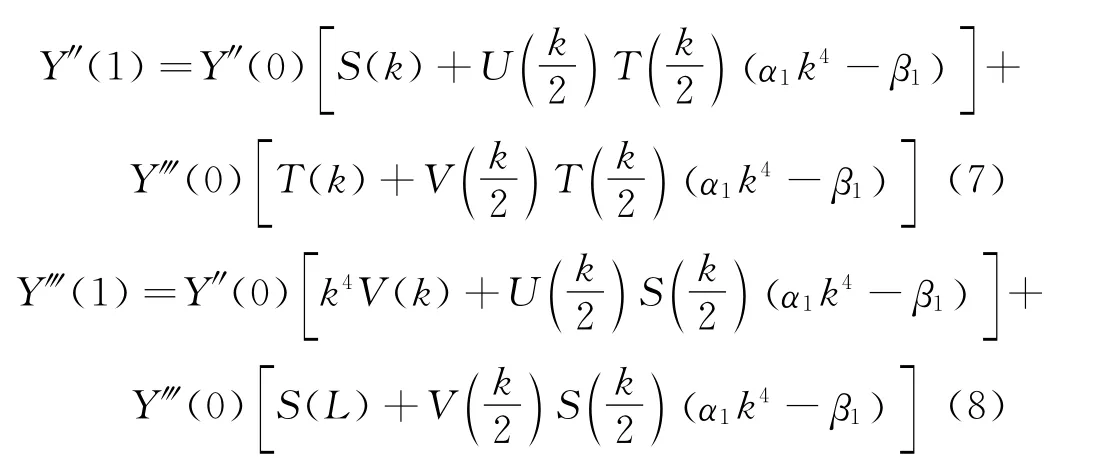
其中：

根据边界条件，式（7）和式（8）可以写成矩阵形式

由此得到相应的频率方程

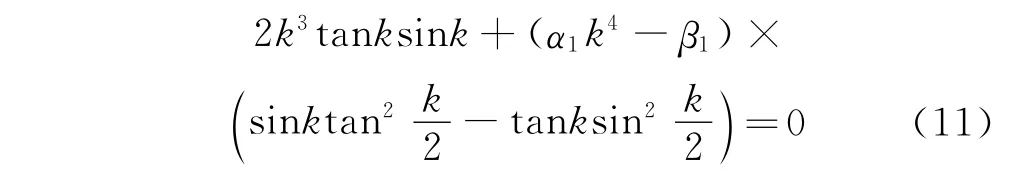
同上推导，即可得出其他简单边界条件的频率方程，这里不再赘述。

1.3 集中质量和弹簧在任意位置时梁的频率方程

在任意位置处含有一个质量和一个集中刚度的悬臂梁如图2所示。

同理可得简支梁的频率方程为

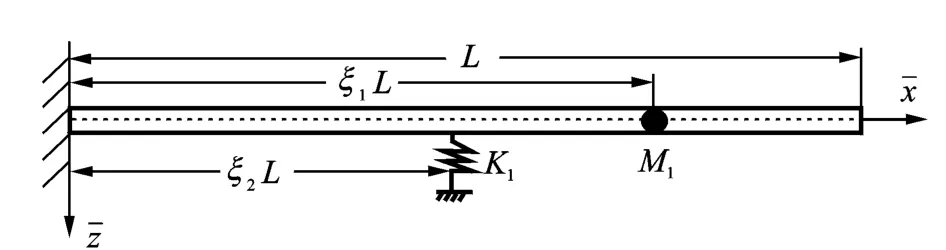
图2 集中质量与集中刚度位于梁任意位置示意图Fig.2 Beam with lumped masses and springs in random position

根据式（6）及悬臂梁的边界条件得振型函数为

其中：

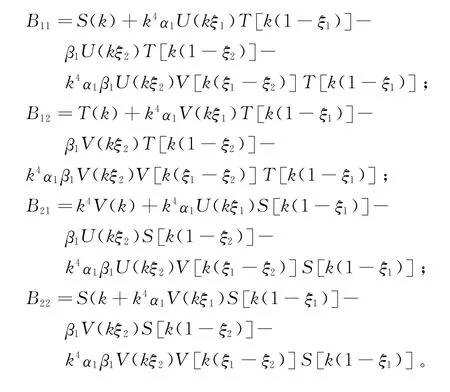
当ξ1＞ξ2时，得到频率方程

其中：

当ξ1＜ξ2，则有

2 模态参数识别方法

采用基于自然激励技术的特征系统实现算法（NEx T-ERA）对梁模态进行识别。

2.1 自然激励技术

自然激励技术针对平稳白噪声激励下的线性系统，结构上两点响应信号的互相关或自相关函数与脉冲响应函数具有相近的表达式［13］。因此可应用互相关或自相关函数代替脉冲响应函数数据。

假设一个N自由度的线性系统，若在系统的第l阶上作用一个稳态的纯白噪声激励信号fl（t），则在结构上第n阶和第p阶的响应信号xnl（t）和xpl（t）的互相关函数［14］为

其中：ψnr为第r阶模态振型的第n阶成分；λr为第r阶特征值；apr为一常量。

根据模态理论，若在系统的第p阶自由度上作用一个脉冲激励力，那么在系统的第n阶自由度处的脉冲响应为

其中：bpr为第r阶模态的参与因子。

比较式（15）和式（16），发现二者形式相同，仅差两个常数项apr和bpr。应用NEx T-ERA方法识别系统模态时，可用互相关函数代替脉冲响应函数。

2.2 特征系统实现算法

特征系统实现算法利用结构的脉冲响应函数矩阵构建广义Hankel矩阵，对其进行奇异值分解得到系统的最小实现，以此识别系统的模态参数［15］。

对N自由度的线性系统，其离散时间的系统状态空间方程在tk+1时刻表示为

其中：k为离散时间步；x（k）为状态向量；u（k）= u（ kΔt）为输入向量；y（k）=y（ kΔt）为输出向量；A，B和C分别为系统矩阵、输入矩阵和输出矩阵。

假设系统在S个自由度上有脉冲输入，在M个自由度上有传感器输出，则ERA算法的数学模型为

设已经得到脉冲响应矩阵h（k），构造广义Hankel矩阵

其中：P=［C CA…CAα-1］T为αM×2N阶可观矩阵；Q=［B AB…Aβ-1B］为2N×βS阶可控矩阵；α和β分别为可观指数和可控指数。

当k=1时，对H（0）进行奇异值分解，得

将式（18）代入式（19）中，整理可得

其中：Σ=［Σn0］为2N×2N阶矩阵。0 0同理，当k=2时，有

设两个辅助矩阵

其中：IM和0M，IS和0S分别为M阶和S阶单位阵和零矩阵。

得到系统的最小实现为

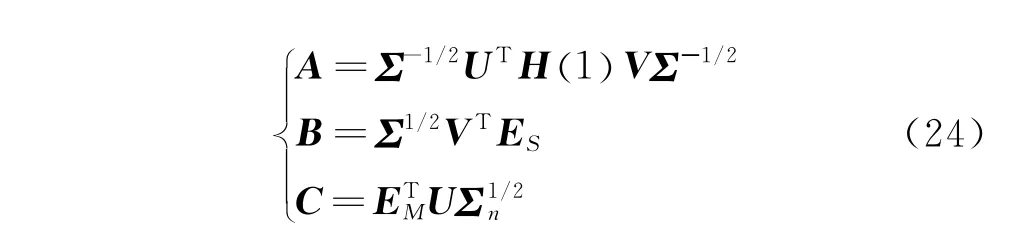
对于离散时间系统，设系统矩阵A的特征值矩阵为Z，特征向量矩阵为ψ，对A做特征值分解，得

对于连续时间系统，Ac的特征向量与A的特征向量相同，特征值满足

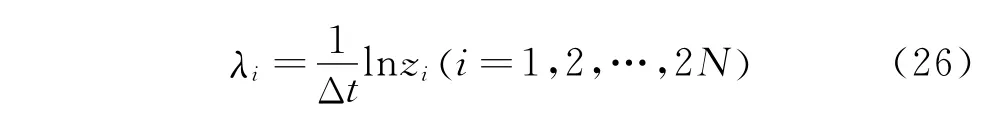
其中：zi为特征值矩阵Z的对角元素；λi为Ac的特征值。

根据模态理论，系统的模态频率、阻尼比和振型为

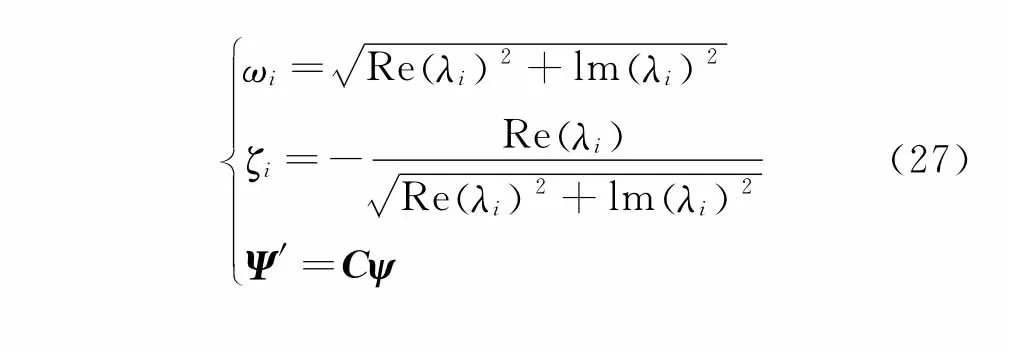
3 数值算例及模态实验

3.1 集中质量和集中刚度大小对固有频率的影响

表1 梁各项参数Tab.1 Material properties of the beam

表2 3种集中质量和弹簧参数Tab.2 Properties of the masses and springs

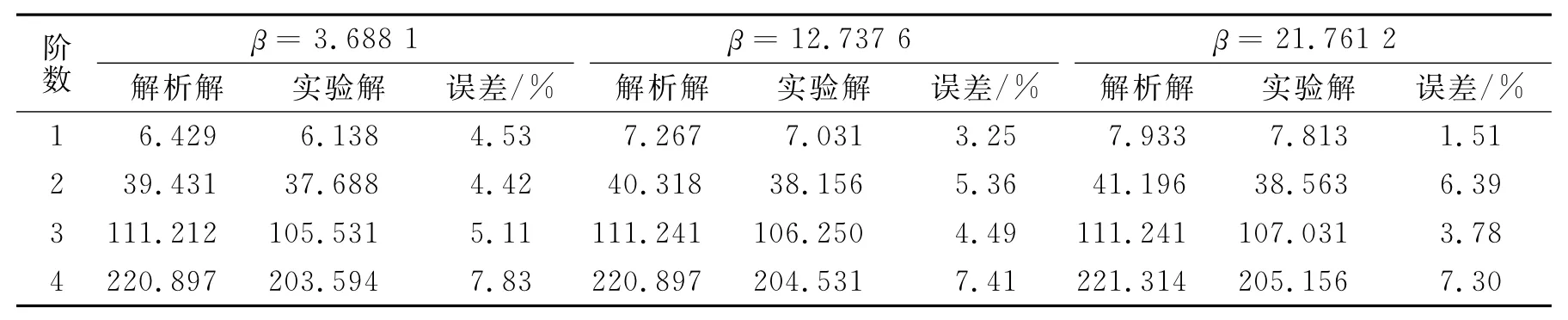
表3 α=0.075 68和β取不同值时的前4阶固有频率ωiTab.3 The first four natural frequenciesωiwhenα=0.075 68，βhas different values Hz

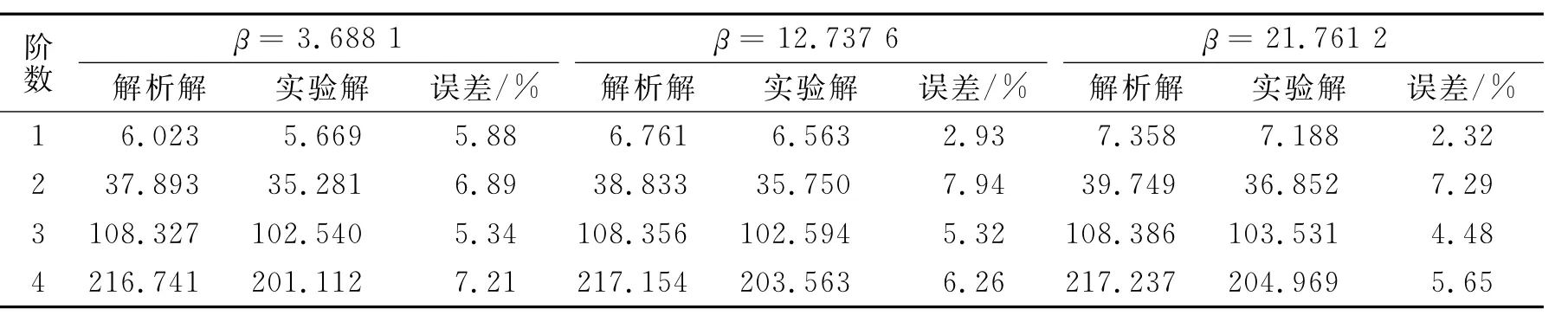
表4 α=0.123 39和β取不同值时的前4阶固有频率ωiTab.4 The first four natural frequenciesωiwhenα=0.123 39，βhas different values Hz

表5 α=0.185 09和β取不同值时的前4阶固有频率ωiTab.5 The first four natural frequenciesωiwhenα=0.185 09，βhas different values Hz

实验时弹簧两端设计有固定装置，可以安装在悬臂梁任意位置处，质量块可用磁座吸附在梁上不同位置。在接近悬臂梁固定端处施加白噪声激励，梁上布置有传感器可测得各点的加速度响应值。实验仪器及模型示意图如图3，4所示。

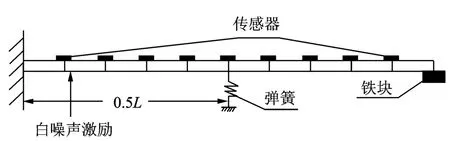
图3 实验模型示意图Fig.3 The experimental model

图4 实验现场Fig.4 Testing ground

分析表3～5可以看出，随着β值的增大，各阶固有频率ωi逐渐增大，即在集中质量和集中刚度位置不变的前提下，若保持集中质量大小不变，当弹簧刚度增加时，各阶固有频率增大。对比分析表3～5，随着α值的增大，各阶固有频率ωi逐渐减小，即当弹簧刚度保持不变而集中质量增大时，各阶固有频率呈减小趋势。通常对于一个单自由度系统，其固有频率与系统刚度成正比，与系统质量成反比。可见，对含有一个集中质量和一个集中刚度的悬臂梁结构，其固有频率变化仍符合这一规律。

将实验结果与理论解对比，很好地验证了这一规律。根据式（12）计算可得悬臂梁在r=1，s=1，xM1=1和xK1=1/2时振型为

在α=0.123 39和β=21.761 2时，梁前4阶模态振型如图5所示。实验识别得到的模态振型如图6所示。对比解析结果与实验结果，二者十分吻合。

图5 解析计算得悬臂梁前4阶模态振型Fig.5 The analytical first four mode shapes

图6 实验识别得悬臂梁前4阶模态振型Fig.6 The first four mode shapes obtained from experiment

3.2 集中质量和集中刚度位置对固有频率的影响

为了探讨集中刚度在梁上位置变化时对梁固有频率的影响，在悬臂梁自由端固定一集中质量，令式（13），（14）中ξ1=1，集中质量系数α1=0.123 39，集中刚度系数β1=21.761 2，当弹簧在梁上的位置为ξ2=0.1，0.2，…，0.9时，分别用本解析方法和实验识别得到了梁的前4阶固有频率。为便于分析，以集中刚度在梁上的相对位置ξ2为横坐标，以解析和实验得到的每一阶固有频率ωi（i=1，2，3，4）为纵坐标，得到ωi的变化曲线如图7所示。其中，图左侧为解析解纵坐标，右侧为实验值纵坐标。

同理，探讨集中质量在梁上位置变化时对梁固有频率的影响。将弹簧固定在梁中，当ξ2=0.5时，令集中质量在梁上移动，取ξ1=0.1，0.2，…，0.9时，通过本解析法和实验得到的各阶固有频率ωi（i=1，2，3，4）随集中质量在梁上相对位置ξ1的变化规律如图8所示。

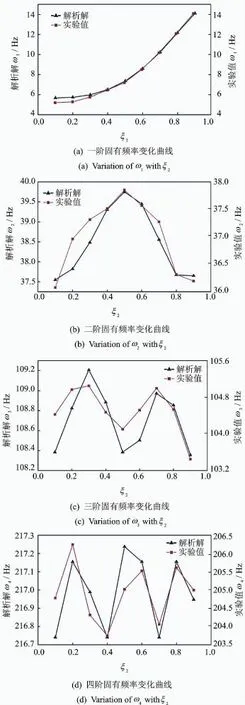
图7 前四阶固有频率随集中刚度位置的变化曲线Fig.7 The variation of the first four natural frequencies with the spring in different positions

图8 前四阶固有频率随集中质量位置的变化曲线Fig.8 The variation of the first four natural frequencies with the mass in different positions

图9 移动弹簧对梁模态刚度的影响Fig.9 The modal stiffness when the spring is in different positions

对集中质量的位置而言，它对固有频率的影响和集中刚度相反。如图10所示，对于一阶模态，当集中质量从固定端向自由端移动时，使梁的振动惯性越来越大，导致梁的一阶模态质量M1越来越大，因而其一阶固有频率ω1逐渐减小，而二阶固有频率ω2先减小后增大。

图10 移动质量对梁模态质量的影响Fig.10 The modal mass when the mass is in different positions

对比实验结果和解析解，实验得到的各阶固有频率的变化趋势和解析结果完全吻合，进一步验证了本研究结论的正确性。

4 结束语

工程中一些结构可以简化成具有集中质量和集中刚度的等直弹性梁，针对这一模型，通过解析方法得出了其在不同边界条件下的固有频率方程和振型函数。通过数值算例求得了含有不同大小集中质量和集中刚度悬臂梁的固有特性解析解，并用NEx TERA法对实际悬臂梁结构的模态进行识别。

将解析结果和实验结果进行了对比，实验结果和解析结构互相吻合，验证了本解析方法的正确性和模态识别方法的有效性。讨论了集中质量和集中刚度大小变化以及它们在梁上的位置变化时对梁固有频率的影响，为工程中具有集中质量和集中刚度的等直弹性梁的振动分析方法和集中参数布置设计提供了参考。

［1］ Gurgoze M.On the eigenfrequencies of a cantilever beam with attached tip mass and a spring-mass system ［J］.Journal of Sound and Vibration，1996，190：149-162.

［2］Lin H Y，Tsai Y C.Free vibration analysis of a uniform multi-span beam carrying multiple spring-mass systems［J］.Journal of Sound and Vibration，2007，302：442-456.

［3］ Rossit C A，Laura P A A.Free vibrations of a cantilever beam with a spring-mass system attached to the free end［J］.Ocean Engineering，2001，28：933-939.

［4］ Banerjee J R.Free vibration of beams carrying springmass systems-A dynamic stiffness approach［J］.Computers and Structures，2012，21-26：104-105.

［5］ Chang C H.Free vibration of a simply supported beam carrying A rigid mass at the middle［J］.Journal of Sound and Vibration，2000，237：733-744.

［6］ Low K H.Frequencies of beams carrying multiple masses：rayleigh estimation versus eigen-analysis solutions［J］.Journal of Sound and Vibration，2003，268：843-853.

［7］ Low K H.On the methods to derive frequency equations of beams carrying multiple masses［J］.International Journal of Mechanical Sciences，2001，43：871-881.

［8］夏季，朱目成，马德毅，带集中质量和弹性支承梁的横向固有振动分析［J］.西南工学院学报，1999，14：1-4.Xia Ji，Zhu Mucheng，Ma Deyi，Analysis of lateral natural vibration of beams with lumped masses and elastic supports［J］.Journal of Southwest Institute of Technology，1999，14：1-4.（in Chinese）

［9］彭献，彭凡，带集中质量的梁弯曲振动特性新的解析表达式［J］.湖南大学学报，2002，29：44-48.Peng Xian，Peng Fan，New analytical expressions of lateral vibration characteristics of a beam with lumped masses［J］.Journal of Hunan University，2002，29：44-48.（in Chinese）

［10］Wu J S，Chou H M.Free vibration analysis of a cantilever beam carrying any number of elastically mounted point masses with the analytical and numerical combined method［J］.Journal of Sound and Vibration，1998，213：317-332.

［11］Li Jun，Liu Chusheng，Li Feng，et al，Modal analysis of a flexible beam attaching multiple absorbers［J］.Applied Mechanics and Materials，2012，226-228：154-157.

［12］孙熙平，王元战，赵炳皓，环境激励下高桩码头物理模型模态实验［J］.振动、测试与诊断，2013，33（2）：263-268.Sun Xiping，Wang Yuanzhan，Zhao Binghao，Modal experiment of physical model for high-piled wharf under ambient excitation［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2013，33（2）：263-268.（in Chinese）

［13］蒋建国，李勤.大型船闸人字闸门工作模态试验分析［J］.振动、测试与诊断，2008，28（4）：390-394.Jiang Jianguo，Li Qin.Operation modal analysis on miter gates of large lock［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2008，28（4）：390-394.（in Chinese）

［14］Xu Junchen，Hong Ming，Cui Hongyu.The Contrast experimental study on operational modal analysis of ship structural model［J］.Applied Mechanics and Materials，2012，226-228：241-246.

［15］Mohanty P，Rixen D J.Modified ERA method for operational modal analysis in the presence of harmonic excitations［J］.Mechanical Systems and Signal Processing，2006，20：114-130.