多自由度超声电机优化设计及在x-y平台的应用*

2015-01-12吴文才刘卫东南京航空航天大学机械结构力学及控制国家重点实验室南京210016

振动、测试与诊断 2015年4期

朱华，吴文才，刘卫东，潘松（南京航空航天大学机械结构力学及控制国家重点实验室南京，210016）

朱华，吴文才，刘卫东，潘松
（南京航空航天大学机械结构力学及控制国家重点实验室南京，210016）

为了探索和快速实现多自由度超声电机的设计及应用，提出一种锥型结构的多自由度超声电机。该电机定子采用单足驱动方式，利用四分区的叠层压电陶瓷作为激励元件，分析其产生两维直线运动的驱动机理。利用有限元软件ANSYS对电机建立参数化模型，并导入到多学科优化软件Optimus中进行全局优化求解。优化结果表明，电机多个设计目标都得以实现，最后制作实验样机并成功应用在x-y平台上。

超声电机；多自由度；优化设计；Optimus；x-y平台

引言

多自由度超声电机作为超声电机的一个分支，是在单自由度超声电机的基础上发展起来的一种新型电机。自20世纪90年代开始成为新型超声电机的研究热点，已有各种形式的电机结构被不断研发出来，如国内学者提出的圆柱-球体多自由度超声电机［1］、四定子多自由度超声电机［2］、方尖塔型二自由度超声电机［3］。日本学者提出的多自由度球面超声电机模组［4］，立陶宛学者提出的4个纵振振子组成的二自由度超声电机定子［5］，而后又发展出更紧凑的单定子型结构［6］。

目前，单自由度超声电机在一维旋转及直线运动领域的应用相对较成熟。随着科技的发展，精密装置对驱动的要求越来越高，若每个自由度的运动都由一台单自由度电机来完成，这必然造成机构复杂、体积庞大、动态性能差等不利因素。因而，研制出性能良好、功能齐全的单一电机来完成多个自由度的驱动输出显得尤为迫切。

在直线平台领域，常见的两自由度x-y平台多为采用两台电机分别驱动负载沿x向导轨和y向导轨运动［7］，或是两台电机分别驱动平行滑块作水平运动，再通过连杆带动中间头作平面轨迹运动［8］。由于两台电机分别驱动，难以做到实时联动定位，尤其是传动机构的限制，难以向微型化方面发展。

针对上述存在的不足，笔者在研究锥形多自由度超声电机定子结构的基础上，将其结构参数作了系统的仿真及参数优化［9］，加工出实验样机，采用有别于传统的电机定子固定的夹持方式［10］，让平板（动子）固定不动，而电机定子支撑板与两维导轨连接在一起，实现电机定子在x-y平台上的自由运动。

本研究方法相比于传统超声电机驱动方式，行程得到有效拓展，活动更加灵活自如，克服了传动机构的死角限制，方便驱动控制实现实时联动定位，简化驱动电路设计，以更小的体积实现传统平台的二维驱动功能。

1 电机工作原理

1.1 结构模型及驱动原理

图1为多自由度超声电机定子结构简图。定子由锥型头、支撑板、叠层压电陶瓷、下配重及预紧螺栓组成。其中：叠层压电陶瓷采用四分区结构沿z轴厚度方向极化，电机定子的工作模态为空间上两个正交的二阶弯振模态及一阶纵振模态，当同时激励出电机定子在x-z平面的弯振模态B2-x与沿z轴的纵振模态L1-z，可驱动压在其上的平板动子沿x轴方向作直线运动，如图2所示。同理，当同时激励出电机定子在y-z平面的二阶弯振模态B2-y与沿z轴的纵振模态L1-z，可驱动压在其上的平板动子沿y轴方向作直线运动。

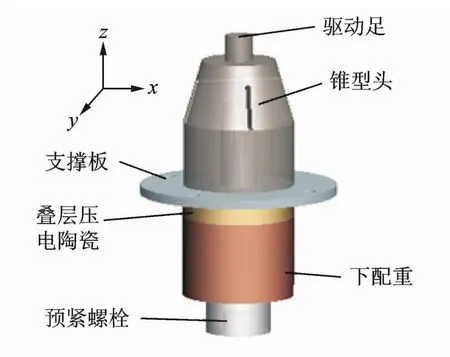
图1 电机结构简图Fig.1 The structure of motor diagram

图2 定子在x-z平面的工作模态Fig.2 The working mode of stator in x-z plane

1.2 陶瓷片结构及对激励信号的要求

叠层压电陶瓷整体尺寸外径×内径×厚度为12 mm×5.5 mm×2.5 mm，实物如图3（a）所示，电气特性如图3（b）所示。4个正极分区分别接正弦激励信号，负极端接信号的地极。

图3 叠层压电陶瓷及其电气特性Fig.3 Laminated piezoelectric ceramics and its electrical properties

假设叠层压电陶瓷片各电极分区分别以A，B，C，D作标记。当对A，B及C，D分别加sinωt，sinωt，cosωt，cosωt正弦信号激励时，可激发出驱动足沿x-z平面逆时针方向椭圆运动轨迹，进而驱动电机定子沿x轴负方向运动，如图4（a）所示。切换A，B及C，D所加正弦信号相位差，可驱动电机定子沿x轴正方向运动，如图4（b）所示。当对A，D 及B，C分别加sinωt，sinωt，cosωt，cosωt正弦信号激励时，可激发出驱动足沿y-z平面逆时针方向椭圆运动轨迹，进而驱动电机定子沿y轴负方向运动，如图4（c）所示。切换A，D及B，C所加正弦信号相位差，可驱动电机定子沿y轴正方向运动，如图4（d）所示。

图4 叠层压电陶瓷的不同激励方式Fig.4 Stacked piezoelectric ceramics with different incentives

2 多自由超声电机有限元模型

在ANSYS13.0软件中建立起多自由度超声电机的1/4映射网格模型，如图5所示。利用APDL语言对定子各个尺寸作全参数化设计，如图6所示。考虑到定子的散热、耐磨性、支撑刚度、加工难易性及选择合适驱动频率段的要求，锥型头及下配重材料选择磷青铜，支撑板材料选择45号钢，预紧螺栓选择M4内六角，材料为304不锈钢，叠层陶瓷片材料为PZT-8。在ANSYS仿真模型中，锥型头、下配重、支撑板及预紧螺栓选用Solid45单元；叠层陶瓷片选择Solid5压电单元。

图5 定子1/4映射网格模型Fig.5 The 1/4 mapped mesh modal of stator

图6 定子参数化模型Fig.6 The parameterized model of stator

由于陶瓷片的尺寸制约着定子整体的结构尺寸，因而定子全参数化设计是以陶瓷片的尺寸为基准，进而构建定子整个结构尺寸参数。由前面对陶瓷片的说明可知，陶瓷片外径R4=6、内径R5= 2.75及厚度H4=2.5固定不变；M4内六角螺栓尺寸R1=1.5，R2=3.5，R3=2，H1=2，H2=2固定不变，而螺栓长度为H3，H4，H5，H6之和。考虑到映射分网的方便，锥面W1为方槽；尺寸R8=1.5固定不变；支撑板安装孔径W2=0.8也不变。实际参数优化尺寸总共11个，分别为H3，H5，H6，H10，R9，W1，H7，H8，H9，R7，W4。

3 Optimus集成优化

Optimus是Noesis Solution公司开发的过程集成和多学科协同优化设计软件，能集成ANSYS仿真工具，实现仿真流程自动化。Optimus允许用户以图形化的方式建立工作流，并在工作流中定义输入文件、输出文件、输入参数、输出参数、所需调用的分析工具及各控件在流程中的逻辑关系。

Optimus软件平台中，集成了多种全局优化算法，如Self-Adaptive Evolution（可进化自适应遗传算法）、Differential Evolution（差分进化算法）、simulated annealing（模拟退火算法）等［11］。全局优化算法能够同时考察设计空间中的参数变量，相比局部优化算法更易达到全局最优解。因此，多自由度超声电机优化设计选择的是Optimus的全局优化算法。

3.1 参数变量及变化范围的定义

考虑到电机合适的工作频率范围、机加工及装配的可行性、ANSYS映射分网的完整性，拟定图6中各设计变量的初值及连续变化范围如表1所示。

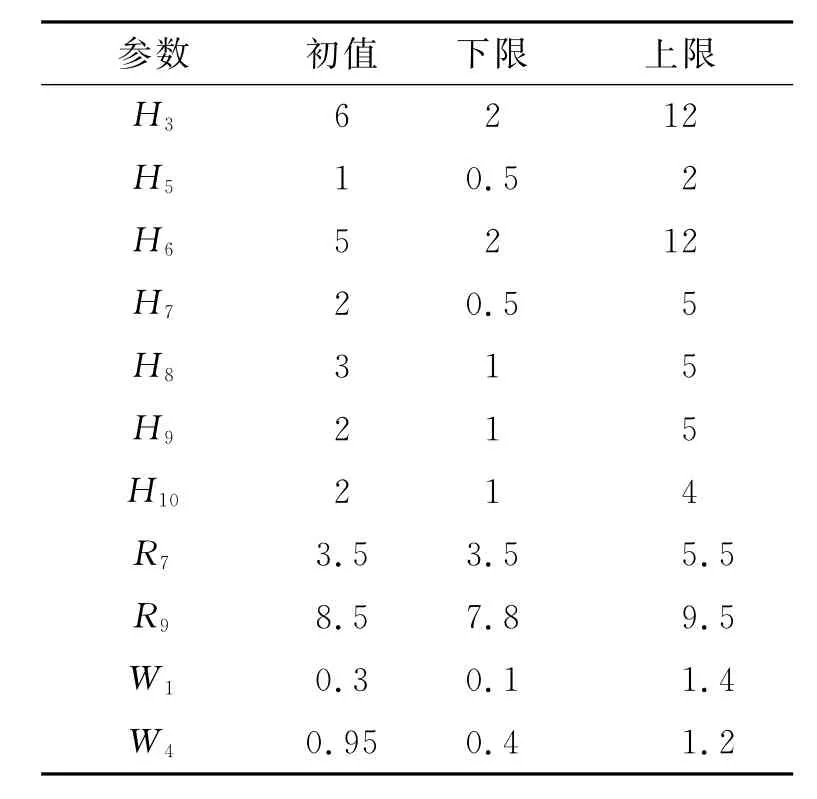
表1 优化变量初始尺寸及上下限Fig.1 The initial size of optimization variables and its limits mm

3.2 目标函数定义及优化方法选择

由于多自由度超声电机二阶弯振模态在x-z平面与y-z平面的空间对称性，可以简化为x-z平面的参数优化为主，兼顾y-z平面优化输出。提取出x-z平面二阶弯振B2-x的振型曲线及沿z轴一阶纵振L1-z振型曲线，如图7所示。作为电机优化迭代过程中模态识别的参考振型，并利用模态置信准则MAC法［12］，在Optimus自动寻优中准确的识别出L1-z及B2-x振型。具体的参数优化过程以下面8个子目标函数分别加以说明。

图7 电机关键位置及振型Fig.7 The modal shape with key position

1）电机的二阶弯振模态B2-x，B2-y的工作频率与一阶纵振模态L1-z的工作频率应尽可能接近，令FRE-MAX，FRE-MIN分别为B2-x，B2-y，L1-z中的最大值与最小值，其子目标函数为

2）电机较小工作模态频率FRE-MIN应远离前一干扰模态频率FRE-FRONT，其子目标函数为

3）电机较大工作模态频率FRE-MAX应远离后一干扰模态频率FRE-REAR，其子目标函数为

4）电机支撑板的中心位置loc-suspend应与二阶弯振中间节点LOC-UX1-ZERO及一阶纵振节点LOC-UZ-ZERO尽量接近，以减少电机工作时支撑处的能量损失，提高效率。其子目标函数为

5）电机的陶瓷片加载正弦电压信号作谐响应时，驱动足沿x轴方向的振幅HAR-UX及沿z轴方向的振幅HAR-UZ都应尽可能大，其子目标函数为

7）陶瓷片的中心PZT/2应与一阶纵振的节点LOC-UZ-ZERO尽量靠近，以有效激发纵向振动模态，其子目标函数为

6）在子目标（5）中要求驱动足沿两个方向振幅尽都可能大的同时，两者振幅比例应趋于相等，即各自所占分量都趋于0.5，其子目标函数为

8）陶瓷片的中心PZT/2应与二阶弯振的波峰LOC-UX2-PEAK尽量靠近，以有效激发二阶弯振模态，其子目标函数为

上述8个函数为多目标优化的子函数，最终优化的目的是要使驱动足在x轴方向及z轴方向的振幅达到最大。

采用主要目标法［13］，即抓住主要目标，兼顾其他要求。笔者选择f5作为主要目标函数，其他7个子目标函数分别给予一定的取值范围，使其转化为新的约束条件，如式（9）所示。通过实践发现，该方法可操作性强，易于导入Optimus软件中自动寻优，有效找出全局最优解。

3.3 优化流程图

利用ANSYS编写的APDL语言建立输入文件76-new-15-UTF.txt及输出文件OPTOUT0611.TXT。在Optimus工作流中，输入参数存放在Input Array1数组控件中，并建立相关监测量如陶瓷片的中心位置PZT/2、支撑板的中心位置loc-suspend等。Optimus通过相应优化算法来不停地调用输入文件，并在输出文件中导出所需监测量与8个子目标函数优化结果，整个优化流程如图8所示。

3.4 优化方法及结果讨论

在Optimus中选择全局优化算法Self-Adaptive Evolution进行迭代计算。在遗传算法中，输入设计参数数量N=11，种群大小为N的4～5倍，笔者将种群大小设置为50，设置最大迭代数量为30，则优化的计算总次数为1 500次。

在寻求主要目标函数f5最大同时应兼顾其余7个子目标约束函数f1，f2，f3，f5，f6，f7，f8，折中选择第1 207次计算数据作为本次优化的寻优结果，其尺寸参数优化结果与圆整值如表2所示。对电机在优化前与优化后8个子目标函数的提取结果作对比，如表3所示。其中，优化前提取结果是指在表1的输入尺寸下，在Optimus作一次单点运算（Nominal）所提取结果。

表2 输入参数优化结果及圆整值Tab.2 The input data derived from Optimization and rounding number mm

表3 各子目标函数优化前后结果对比Tab.3 Each sub-objective results were present before or after optimization

图8 Optimus中整体流程图Fig.8 The flow char in Optimus

从表3的优化前与优化后的数据结果对比可知，电机驱动足沿x轴方向与z轴方向的振幅之和f5明显增大了一个数量级，且沿x轴方向与沿z轴方向所占分量值f6接近0.5，达到了主要设计目标。电机支撑板的中心位置与二阶弯振中间节点及一阶纵振节点位置的重合度指标f4比优化前降低了两个数量级，几乎趋近于0，有利于电机应用于x-y平台减少能量耗散及降低对平台的干扰。同时工作频率与前后干扰频率差f2，f3最小达到8 k Hz以上，有效防止电机加正弦信号激励及调频调速时把不期望的干扰模态激发出来，不利于电机的夹持，严重时会产生较大的噪声干扰。在保证实际应用需求的前提下，子目标函数f1，f7，f8变化不大，可以作为次要目标考虑。总体而言，优化后电机各项性能得到显著提高，验证了模型的正确性及算法的可靠性。

4 样机制作和x-y平台应用

4.1 实验样机制作及实验

加工制作的电机实物如图9所示。利用德国Polytec公司的PVS-300F多谱勒激光测振仪对电机定子进行扫频测振实验，测得电机横向频响曲线及纵向频响曲线，如图10，11所示。与仿真计算结果进行对比，如表4所示。可以看出，仿真计算频率与实际加工样机测振频率比较接近，在二阶弯振处存在最大误差，达到400 Hz左右，这与电机加工装配和仿真计算两方面都存在误差有关。

图9 电机实物图Fig.9 The photos of motor

表4 电机扫频测试与仿真对比Tab.4 The frequency in sweep experiment and simulation

图10 x向二阶弯振频响曲线Fig.10 The curve of second lateral vibration in x axis

图11 z向一阶纵振频响曲线Fig.11 The curve of first longitudinal vibration in z axis

4.2 x-y平台及性能测试

将制作的实验样机装配到x-y工作平台上，如图12所示。传统多自由度超声电机的工作模式是定子固定不动，而动子如直线导轨、旋转球等往复移动或转动。本工作台中电机工作方式与之相反，把多自由度超声电机定子通过支撑板装配在两自由度导轨上，而下面的氧化锆摩板固定不动，当对定子陶瓷片各分区分别施加正余弦信号激励时，驱动足产生椭圆轨迹，依靠氧化锆平板对定子的反作用力驱动其实现沿x轴方向或y轴方向作两自由度直线运动。

图12 x-y工作平台Fig.12 The photos of x-y platform

4.3 电机在x-y平台上性能测试

图13为平台上电机沿x轴向及y轴向运动性能测试方案。其中，电机空载线速度v是以测试电机来回跑10趟所需时间换算得出。加负载时，由于线速度较慢及同向负载影响，以电机带负载走一趟所需时间换算出线速度。平台中电机x轴向行程S1=58 mm，y轴向行程S2=60.5 mm。当驱动电路给予电机合适的激励频率f（65～70 k Hz）、激励电压（峰峰值35～50 V），测出电机速度v及负载物重G如表5所示。表5中负载G为0 N对应空载线速度v最大值，随着负载G逐渐增大，线速度v趋于0。

表5 x-y平台电机测试结果Tab.5 The experiment results of x-y platform

5 结束语

针对多自由度超声电机的结构优化问题，从驱动机制和参数优化模型方面作了系统阐述。在Optimus中应用遗传算法对如何提高电机驱动足振幅、减少电机工作时能量耗散、降低对支撑系统干扰及减小激励频率干扰进行了研究，得到的优化结果验证了算法的可靠性。加工出的实验样机创新性地将多自由度超声电机成功应用于两自由度的x-y工作平台上，为多自由度超声电机向实际应用方面迈出了一步，并为下一阶段的x-y平台行走轨迹控制打下基础。

［1］ Zhao Chunsheng，Li Zhirong，Huang Weiqing.Optimal design on stator of cylinder-sphere 3-DOF ultrasonic motor using structural dynamics method［C］∥Ultrasonics Symposium，2004 IEEE.Nanjing：IEEE，2004，3：2259-2262.

［2］傅平，郭吉丰，沈润杰，等.二自由度行波型超声波电机的驱动和运动姿态控制［J］.电工技术学报，2008，23（2）：25-30.Fu Ping，Guo Jifeng，Shen Runjie，et al.Driving circuit and position control system of two degree-of-freedom spherical traveling-wave type ultrasonic motor ［J］.Transactions of China Electrotechnical Society，2008，23（2）：25-30.（in Chinese）

［3］金家楣，张建辉，赵淳生.新型方尖塔形定子二自由度超声电机的结构设计、驱动机理与性能研究［J］.振动与冲击，2009，28（12）：63-67.Jin Jiamei，Zhang Jianhui，Zhao Chunsheng.Research on construction，principle，and performances of a novel two-degrees of freedom ultrasonic motor with an obelisk stator［J］.Journal of Vibration and Shock，2009，28（12）：63-67.（in Chinese）

［4］ Mashimo T，Awaga K，Toyama S.Development of a spherical ultrasonic motor with an attitude sensing system using optical fibers［C］∥Robotics and Automation，2007 IEEE International Conference on.Roma，Italy：IEEE，2007：4466-4471.

［5］ Vasiljev P，Borodinas S，Yoon S J，et al.The actuator for micro moving of a body in a plane［J］.Materials Chemistry and Physics，2005，91（1）：237-242.

［6］ Vasiljev P，Borodinas S，Mazeika D，et al.Investigation of the multipurpose piezoelectric actuator［C］∥Proceedings of the Second International Workshop on Piezoelectric Materials and Applications in Actuators.Paderborn：Heinz Nixdorf Institute，2006：339-408.

［7］张健滔，朱华，赵淳生.杆式超声电机在精密平台上的应用［J］.中国机械工程，2011，15（22）：1842-1846.Zhang Jiantao，Zhu Hua，Zhao Chunsheng.Precision positioning stage using rod shape rotary ultrasonic motors［J］.China Mechanical Engineering，2011，15（22）：1842-1846.（in Chinese）

［8］ Sun Shuwen，Wu Na，Zheng Gang，et al.Research and implementation on control technology of plane two-DOF dual-truck parallel mechanism［C］∥Mechatronics and Automation（ICMA），2011 International Conference on.Beijing：IEEE，2011：1682-1687.

［9］时运来，赵淳生.蝶形直线超声电机优化设计［J］.振动、测试与诊断，2012，32（6）：883-891.Shi Yunlai，Zhao Chunsheng.Application of response surface methodology for optimization of butterflyshaped linear ultrasonic motor［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（6）：883-891.（in Chinese）

［10］姚志远，赵妹淳，江超，等.扇形直线超声电机的结构设计［J］.振动、测试与诊断，2013，33（1）：40-43.Yao Zhiyuan，Zhao Meichun，Jiang Chao，et al.Structural design on linear ultrasonic motor with fanshaped stator［J］.Journal of Vibration，Measurement ＆amp；Diagnosis，2013，33（1）：40-43.（in Chinese）

［11］王雪梅，王义和.模拟退火算法与遗传算法的结合［J］.计算机学报，1997，20（4）：381-384.Wang Xuemei，Wang Yihe.The combination of simulated annealing and genetic algorithms［J］.Journal of Chinese Computers，1997，20（4）：381-384.（in Chinese）

［12］Allemang R J，Brown D L.A correlation coefficient for modal vector analysis［C］∥Proceedings of the 1st International Modal Analysis Conference.Orlando：［s.n.］，1982：110-116.

［13］王国强，赵凯军，崔国华.机械优化设计［M］.北京：机械工业出版社，2009：160-180.