超声导波相移追踪的回波辨识方法*

2015-01-12刘小峰付立斌重庆大学机械传动国家重点实验室重庆400044

振动、测试与诊断 2015年4期

柏林，刘小峰，付立斌（重庆大学机械传动国家重点实验室重庆，400044）

超声导波相移追踪的回波辨识方法*

柏林，刘小峰，付立斌
（重庆大学机械传动国家重点实验室重庆，400044）

超声导波的多模式和频散特性使得其回波分析与定位异常复杂，在导波传播的模型解析的基础上，提出了一种基于频率相位追踪的回波辨识方法。首先，选取指定模式的直接散射信号的频域相位作为参考相位，将被分析信号各个波包的频域相位用参考相位进行归一化处理，得到各个波包相对参考波包传播距离的归一化阶次；然后，结合回波信号的传播路径分析，达到对各个波包定位辨识的目的。数值仿真和实验也验证了该方法的可行性和有效性。

超声导波；频散特性；相移追踪；回波辨识

引言

由于超声导波具有检测效率高、速度快、衰减小和可长距离传播等优点，在国内外无损检测和结构健康监测方面得到了广泛的应用［1］。超声导波是由合适的换能器在结构的某一位置上激发的能量短脉冲入射信号。超声导波的多模式和频散特性使信号波包的形状随着传播距离的变化而变化，峰值幅度随传播距离的增加而减小，信号信噪比降低，增加了信号特征的提取与辨识难度［2］。针对Lamb信号处理的复杂性，许多信号处理方法如短时傅里叶变换［3］、小波变换［4］、希尔伯特-黄变换［5］、自适应匹配法［6］和时频相关分析方法［7］等都被应用于Lamb波信号特征的提取。必须指出的是，这些传统方法的应用除了未充分考虑Lamb的频散效应外，还必须依据可靠的基准信号，对波包进行分析与识别。然而，这种基准信号参考法容易受外界条件变化的影响，造成波包辨识的误差。为了减少对基准信号的依赖性，文献［8-9］利用声互易性原理，提出了时间反转法实现Lamb波的空间聚焦和时间压缩。这种方法不需要参考基准，但只适用于单模式波包分析。

1 Lamb波传播的模型解析

应力波在传播过程中会受频散效应的影响，导致波包形状时频空间的扩展变形。为了更好地研究这种散射特性，有必要对Lamb波在波导中的传播特性进行模型解析。假设激励信号g（t）沿着波导传播到达距离激励点x处时的导波信号为

其中：t为时间；cp为该模态导波的相速度。在频域上，该导波信号表示为

其中：Sx（ω）为sx（t）的傅里叶变换；G（ω）为g（t）的傅里叶变换；k（ω）=ω/cp为与各模式波的频散特性相对应的频率波数曲线。

由式（2）可知，当激励信号传播到x位置时，G（ω）将产生e-jk（ω）x的相移。一般情况下，导波信号在介质中传播时的反射与透射系数受频率影响不大，可看作与频率无关的常数。实标波包在传播距离x后可表示为

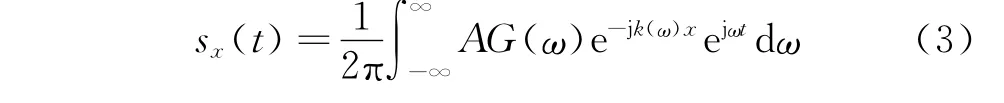
其中：A为与ω频率无关的衰减系数。

式（3）表明，传感器接受的波包形状取决于波数频率曲线k（ω）及传播距离x。当导波模式不同时，k（ω）的形式也不同。激励信号选择为式（4）中Gabor脉冲

其中：参数ξ/2π和σ分别为频率中心和时宽。

试验过程中，在掘进机左右两端和前端布置挡板，试验过程中，掘进机平台不动，通过移动挡板模拟掘进机在巷道中偏航位移和车前距的变化。车前距通过2个激光传感器平均值获得，偏航位移通过2个超声传感器测距差值绝对值除以2获得，得出车前距和偏航位移测试结果见表3和表4，车前距的测试误差为0.006 m，偏航位移测试误差为0.024 m。

g（σ，ξ）（t）的傅里叶变换为

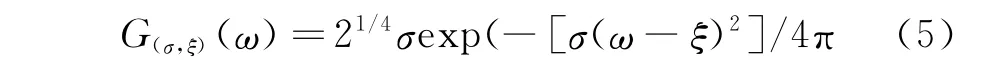
波数频率曲线在中心频率处采用泰勒公式进行高阶多项式展开，一般情况下，k（ω）二阶多项式足以表示模式波的频散特性。

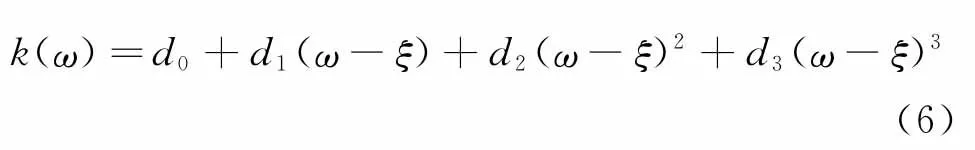
实标导波检测中，波导存在裂纹或一些不连续问题，除了频散特性引起的相移外，波包的频率相位还会发生额外偏移，且实标传感器测得的信号包含经由不同路径传播不同距离的多个频散波包。传感

器测得的波包表示为

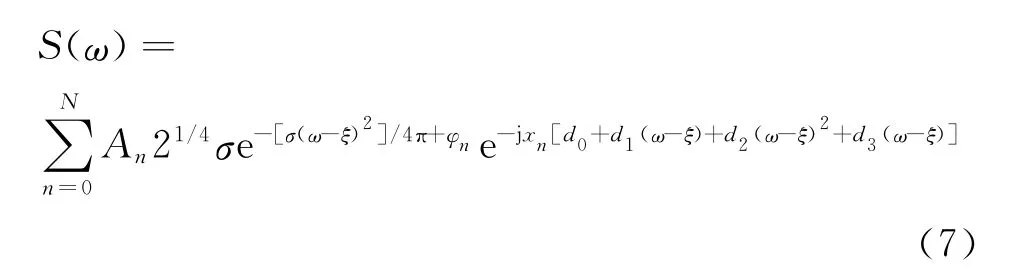
其中：ejφ为额外的相移；xn为激励波包沿第n条路径传播的距离；An为第n条路径的波包衰减系数。

假如导波从激振器激直接传播至距离x0处的传感器的过程中没有任何结构反射，则该波包可表示为

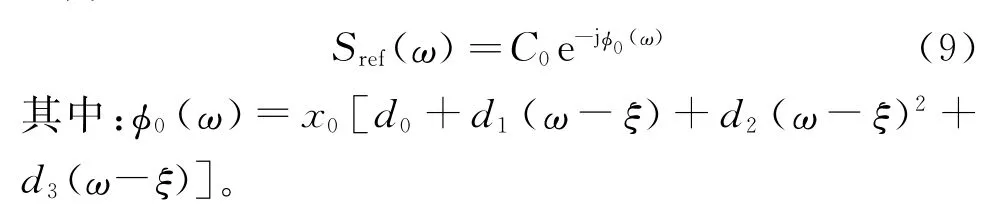
设ordern=xn/x0，则φn（ω）=ordernφ0（ω），则式（8）可以表示为

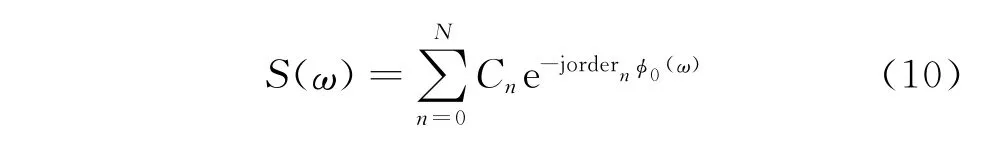
从式（10）可知，ordern与波包传播距离xn之间有着一一对应关系。笔者引入了旋转机械中的阶次理论求解每个波包在波导传播的实标距离xn。阶次追踪技术是针对旋转机械转速变化过程中非平稳信号提出的等角度采样归一化转频的信号分析方法［10-11］。其主旨是通过信号处理算法将等时间间隔采样信号转化为等角度采样信号，将与转轴速度密切相关的旋转部件振动和噪声归一化为转频的谐波分量，避免转速变化带来的频率模糊问题。超声导波的波数曲线随频率变化的非平稳特性类似于旋转机械振动信号随转速的变化的非平稳特性。因此，如果将特定模式的直接散射波的相位作为参考，由于同模式的波包的频域相位与参考相位具有严格的线性关系，只要求解出与其相对参考相位的归一化阶次，结合参考波包的实标传播距离，就可获得每个波包的实标传播距离，而与参考波包不同模式的波包将会作为噪声排除。也就是说，只要将指定模态的φ0（ω）作为参考相位，在没有基准信号的情况下，也可以对各个波包进行模式识别及定位分析。

2 数值仿真

为了验证本研究方法的可行性，用数值模拟的方法进行验证。采用ABAQUS/Explicit瞬态动力分析方法对铝梁中超声Lamb波传播进行数值模拟。铝梁模型长为2 000 mm，宽为40 mm，厚为1 mm，铝梁模型尺寸如图1所示。网格类型采用CPE4R单元。采用式（4）中的Gabor脉冲，在距离铝梁左端350 mm处垂直施加瞬时压力来模拟入射S0模式纵波。其中：σ=5×10-6；ξ=2π×140 k Hz；时间中心在15μs处。S0模式波在激励信号中心频率处的群速度为2.583 mm/s。模型在传感器位置1处接收参考波包，在传感器位置2处接收分析波包。

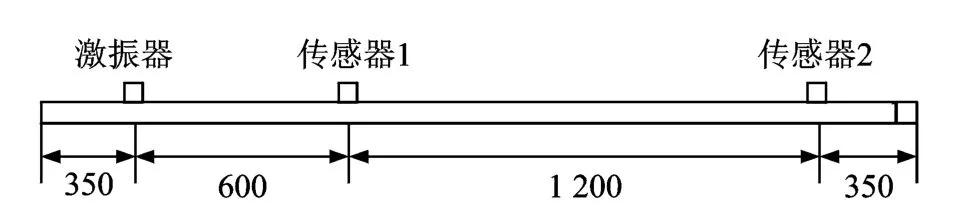
图1 仿真模型原理示意图（单位：mm）Fig.1 Schematic of simulation model（unit：mm）

传感器1处的参考波包采集时间设置为0.4 ms，图2为参考波包Sref（t）的时域波形，其包络峰值时间点约为240μs。如按传统波包传播距离计算方法，传感器1与激振器的距离为2.583 mm/μs×（240μs-15μs）=581 mm，与实标传感器1的位置（600 mm）相差19 mm。

传感器2处接收的单个分析波包的采集时间设置为0.9 ms，其时域波形及频谱如图3所示。被分析波包的包络峰值时间点约为687μs，按照传统方法估算传感器2与激发点的距离为1 736 mm。这与实标传感器2的位置（1 800 mm）相差64 mm。可见，由于超声导波的频散特性，按照传统峰值估计方法计算出的波包传播距离的误差会随着导波传播距离的增加而变大。

图2 距离激振器600 mm处采集到的参考信号Fig.2 Referenced signal at 600 mm captured away from the actuator

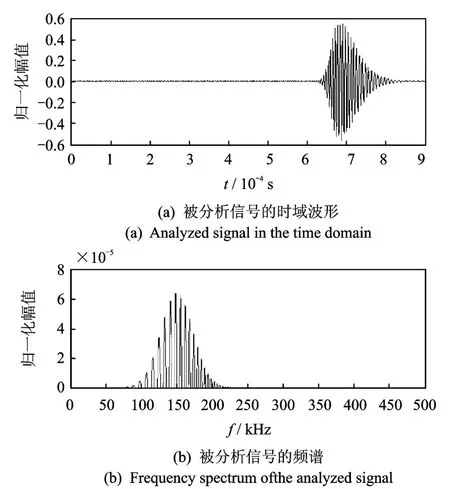
图3 距离激振器1 800 mm处采集的信号Fig.3 Analyzed signal captured at 1 800 mm away from the actuator

采用笔者提出的方法，对图（2）中参考信号的傅里叶变换采用希尔伯特-黄变换求解相位的方法，得到其频域相位为

其中：H Sref（ω［］）为Sref（ω）的希尔伯特-黄变换。

参考波包的频域相位去卷叠处理后如图4所示，参考波包的频域相位随着频率的增加而成曲线变化。这种曲线变化关系造成了波包的时域扩展的散射特性。图4中的相位特性曲线满足光滑连续的条件，对其进行分段处理，在分段的小范围内用φi（f）=aif2+bif+ci的二次多项式进行曲线相位拟合。根据拟合曲线来计算等相位频率点Fn

其中：Δθ为等角度增量。

如图5所示，根据等相位频率点Fn对图3（b）中的被分析信号傅里叶变换进行插值，实现频域信号的等角度插值重采样，得到阶比采样的角域离散转角序列S（Fn）。利用离散转角序列S（Fn）即可通过傅里叶变换获得被分析信号的阶次谱，如图6所示。

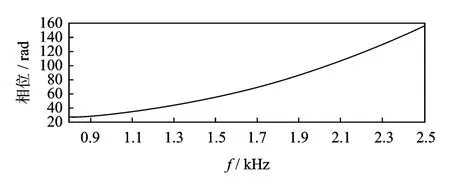
图4 展开后的相位特性Fig.4 Unwrapped phase

图5 重新采样的频谱Fig.5 Resampled frequency spectrum

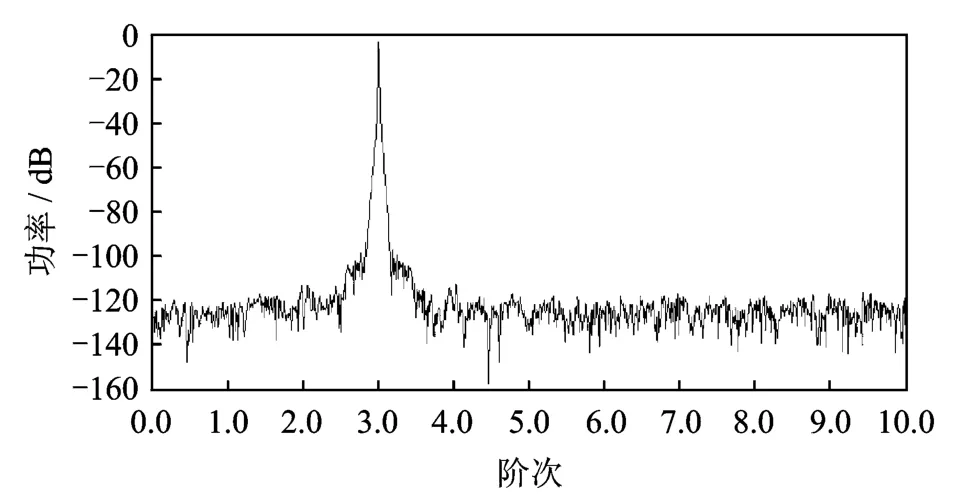
图6 被分析信号的阶次谱Fig.6 Order spectrum of the analyzed signal

从图6中可以看出，在阶次3处有明显的峰值。根据提出的相移阶次追踪原理，第3阶次表示被分析信号的频域相位对参考波包频域相位的归一化频率为3。根据式（10）中相位变化与阶次的关系，结合参考波包的实标传播距离为600 mm，图3被分析波包的实标传播距离为3×600 mm=1 800 mm，正好对应着获得被分析波包的传感器2距离激发点的实标距离。可见，笔者提出的方法比传统的峰值估计定位方法更能准确地进行自参考的散射导波传播距离的估计。

3 实验验证

实验采用铝板模型，其二维几何构型及传感器布局示意图如图7所示。采用Standford Research DS345信号发生器产生Gabor脉冲，信号经由Krohn Hite model 7500信号放大器放大后对铝板进行激发。由激光多普勒测振仪采集的电压信号输入到Tektronix TDS420A示波器后，进入计算机进行显示与处理，采样频率为10 MHz。由于在140 k Hz×1 mm频率下有A0和S0两种模式波，其中S0模式波具有非常小的面外位移量，且其在传播过程中衰减很快，因此测试系统主要检测到的是A0模式的Lamb波。A0模式传播群速度为2 069 m/s。

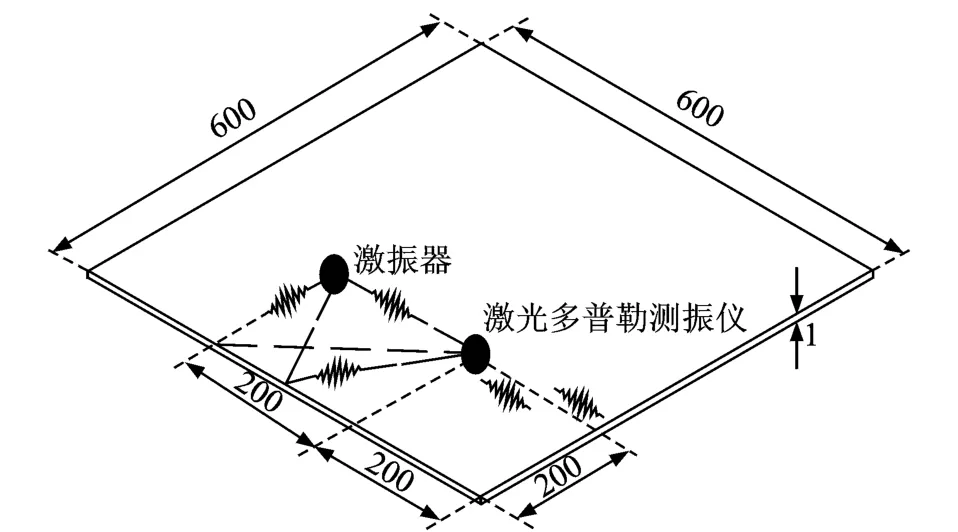
图7 铝板几何构型及传感器布局示意图（单位：mm）Fig.7 Geometry and actuator/sensor layout of the aluminum plate（unit：mm）

根据激光测振仪测得采样时间为350μs的时域信号如图8所示。可见，采集信号中边缘的回波和噪声干扰使波包的辨识异常复杂。采用本研究方法，把第1个波包（从激励点直接传播到测振点的第1个直接散射波）作为参考波包。由A0波的传播速度可知，该直接散射波包传播至测振点的理论时间约为112μs，与采集的分析信号中第1个波包的包络峰值点109μs有差距。参考波包的采集时间设置为150μs。图8中，由于边界反射波包幅值衰减快，加上强干扰噪声及频散现象的影响，很难辨识出在200μs～280μs之间波包数量及各自到达时间点。

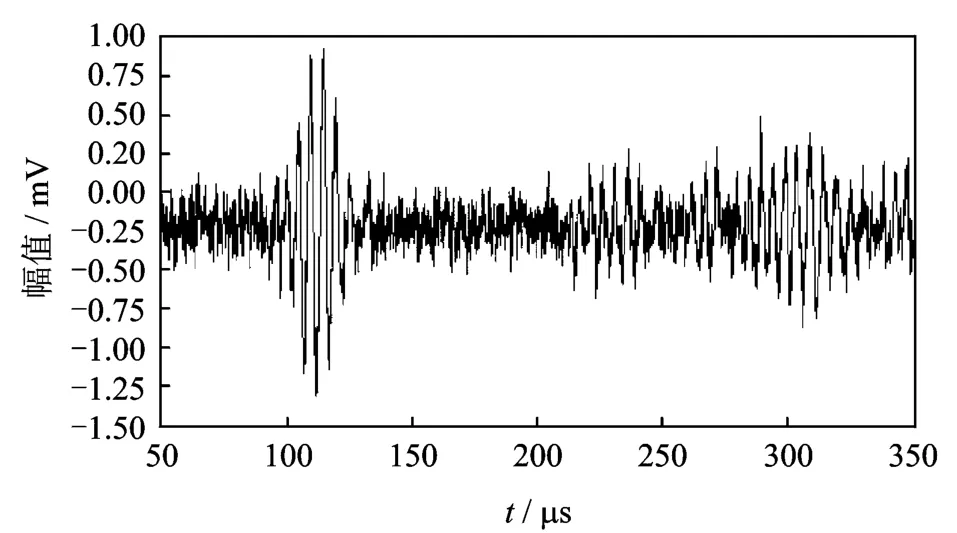
图8 实验产生的传感器信号Fig.8 Resulting sensor signal in the experiment

图9 处理后传感器信号的阶次频谱Fig.9 Order spectrum of the processed sensor signal

4 结束语

提出自参考的Lamb回波辨识方法，采用相移追踪的方法，能够有效地对复杂导波信号中的各个回波进行定位分析。仿真和实验表明，该方法除了有较好的抗干扰性能外，在强散射情况下，也能对各波包传播距离进行准确估计。在波包模式识别方面，只要选择不同模式的参考波包，其他模式的波包在分析中就会当做是噪声被排除开来，因此该方法可有效地进行波包模式的识别。由于模式波包在发生模式转换时，其频域相位与散射曲线之间不再具有严格的线性关系，因此该方法不适用于模式转换波包的识别。另外，该方法的准确性很大程度上决定于直接传播信号的频域参考相位的提取。能否准确提取参考相位，将直接影响后续的波包定位精度。尽管该方法还有许多待改进之处，但作为一种自参考无基准波包识别方法，将为无损检测和结构健康检测提供新的工具，具有较好的应用前景。

［1］袁慎芳.结构健康监控［M］.北京：国防工业出版社，2007：78-82.

［2］ Raghavan A，Cesnik C E S.Review of guided-wave structural health monitoring［J］.Shock and Vibration Digest，2007，39（2）：91-114.

［3］ Hong J C，Sun K H，Kim Y Y.Dispersion-based short-time Fourier transform applied to dispersive wave analysis［J］.Journal of the Acoustical Society of America，2005，117（5）：2949-2960.

［4］ Paget R P，Sorrivi E，di Scalea F L，et al.Waveletbased outlier analysis for guided wave structural monitoring：application to multi-wire strands［J］.Journal of Sound and Vibration，2007，37（1-2）：52-68.

［5］张海燕，于建波，孙修立，等.HHT在Lamb波检测信号分析中的应用［J］.振动、测试与诊断，2010，30（3）：223-226.Zhang Haiyan，Yu Jianbo，Sun Xiuli，et al.Analysis of Lamb wave signal using Hilbert-Huang transform ［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2010，30（3）：223-226.（in Chinese）

［6］ Li Fucai，Su Zhongqing，Ye Lin，et al.A correlation filtering-based matching pursuit（CF-MP）for damage identification using Lamb waves［J］.Smart Materiel and Structure，2006，15（6）：1585-1594.

［7］ Raghavan A，Cesnik C E S.Guided-wave signal processing using chirplet matching pursuits and mode correlation for structural health monitoring［J］.Smart Materials and Structures，2007，16（2）：355-366.

［8］ Park H W，Sohn H，Kincho H L，et al.Time reversal active sensing for health monitoring of composite plate［J］.Journal of Sound and Vibration，2007，32（1-2）：50-66.

［9］ Gangadharan R，Murthy C R L，Gopalakrishnan S，et al.Time reversal technique for health monitoring of metallic structure using Lamb waves［J］.Ultrasonics，2009，49（8）：696-705.

［10］Brandt A，Lago T，Ahlin K，et al.Main principles and limitations of current order tracking methods［J］.Journal of Sound and Vibration，2005，39（3）：19-22.

［11］Liu Xiaofeng，Bo Lin，Veidt M.Tonality evaluation of wind turbine noise by filter-segmentation［J］.Measurement，2012，45（4）：711-718.