固液界面动电效应的研究进展*

郭万林，费雯雯

◀专家论坛▶

固液界面动电效应的研究进展*

郭万林1，2，费雯雯1，2

（1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016）
（2.南京航空航天大学纳智能材料器件教育部重点实验室 南京，210016）

动电效应是1807年以来发现的发生在固液界面的一系列流动生电或电致流体运动的现象的总称。该效应广泛地应用于工业生产、物质的分离、提纯、检测和水净化等。动电效应的本质来源于界面双电层的作用。笔者回顾了动电效应的历史发展，介绍了双电层的物理模型，对几种重要的动电现象进行理论分析综述，并结合笔者研究团队在石墨烯中发现的新的动电效应做了分析展望。

动电效应；固液界面；双电层；石墨烯

引 言

动电效应在科学研究和工业生产过程中被广泛应用于物质的检测与分析。微纳体系中的一些动电现象为新型传感和能量转换提供可能。笔者首先回顾了动电效应的发现历史，对其物理本质——双电层进行介绍；然后，对几种重要的动电现象在微纳尺度进行了理论分析，结合笔者研究团队在石墨烯中发现的新的动电效应，阐明了其与传统动电现象的差异；最后，总结及展望动电效应的实际应用。

1 历史发现

动电现象，又称电动现象。它的发现可以追溯到19世纪初期。1807年，Ferdinand Friedrich Reuss在莫斯科进行了两项实验：a.在一个装有水的U型管内放置黏土塞，对水通直流电，一端U型管内的液面会上升；b.在黏土上方放入石英砂，再施加直流电场时发现黏土粒子在砂层里面定向移动。Reuss的这两个实验现象即目前所熟知的电渗效应（electro-osmosis）和电泳现象（electro-phoresis）［1］。在此之后，许多科学家如Wiedemann［2］和Wall等［3］对Reuss发现的电动行为尤其是电渗效应进行了大量的定量研究。1859年，Quincke［4］在研究电渗效应的同时发现了电渗的逆效应。他用管子抽取水的过程中，在管子的两端测到电势差，这意味着流动电位（streaming potential）现象的发现。Quincke还研究了一系列参数对流动电位的影响，发现流动电压与横截面积无关，与两端压强差线性相关，并且加入盐溶液会降低流动电压等。他假设材料的表面带电，并且外层分布着空间电荷，符号与带电表面相反，以此来定性解释电渗效应和流动电位的实验现象。1879年，Helmholtz［5］用双电层理论定量分析了动电现象，并将动电传递的电参数与流参数联系起来。另一种经典的动电现象为沉降电位（sedimentation potential），于1880年由Ernst Dorn发现。他在一个装有水的垂直玻璃管中洗涤沙粒，随着沙粒的沉降，埋置在玻璃管两端内的电极具有电势差［6］。

除了电泳、电渗、流动电位和沉降电位这4种经典的动电现象以外，科学家们又相继发现了一些新的动电效应。1933年，Debye［7］发表了一篇论文预测置于高频声场中的电解液，由于阴阳离子质量和摩擦因数的差异导致不同的位移振幅，从而会产生交变的电场，即离子振动电位（ion vibration potential）。当时这样的实验不太容易实现，直到Rutgers［8］指出碘化银溶胶体系中该德拜效应可能会较为显著。Rutgers随后成功地在三硫化二砷溶胶中实现了德拜效应［9］，并称之为超声振动电位（supersonic vibration potential）。现在这种基于电-声的动电效应常被用来测量电泳淌度和粒径。1947年，Boris Vladimirovitch Derjaguin课题组理论预测并在实验上验证了扩散电泳（diffusiophoresis）的现象［10］。扩散电泳即指胶体粒子在电解液浓度梯度下自发的运动。与之相对应的逆效应为毛细渗透（capillary osmosis）［11］。2014年，本课题组研究发现石墨烯与流体界面耦合产生新的动电效应：拽势（drawing potential）［12］和波动势（waving potential）［13］，并从理论上分析阐明了该动电机制。

2 动电现象的双电层理论

2.1 界面电荷来源

1884年，Svante August Arrhenius提出电解质解离的概念，但未受到广泛关注。1886年，Jacobus van＇t Hoff研究氯化钠溶液渗透压时发现，其数值是非解离氯化钠盐的两倍，至此，电解质解离的概念才被接受。目前，界面电荷来源大致分以下4类：

1）电离作用。固体表面功能团在溶液中发生电离，使固体表面带电。例如，固体表面含有酸、碱基团，在溶液中发生电离，表面带负或正电荷。

2）离子晶体不对称电离。例如，碘化银晶体在水中溶解，Ag+相较于I-会优先电离，使得其表面带负电。

3）离子交换作用。例如，当玻璃与CaCl2水溶液接触时，玻璃中硅酸钠的钠离子可被钙离子取代，使得玻璃表面带正电。

4）离子吸附作用。在一般情况下，固体物质在溶液中选择性地优先吸附某种离子（包括一些分子），与组成成分性质越相似的离子越易吸附。若固体表面吸附的是正离子，则该表面带正电，反之带负电。

2.2 双电层理论模型

2.2.1 Helmholtz双电层模型

目前一般认为，最原始的双电层概念于1853年由Helmholtz提出［14-15］，也有学者认为Helmholtz是基于Quincke的双电层思想［3］。但无论是Helmholtz还是Quincke，他们的双电层都是简单的平板电容模型。图1为Helmholtz的双电层平板电容模型示意图。图中：正、负电荷整齐地排列在界面层的两侧；φ0为固体表面电势，在平板电容器内电势φ直线下降，两层间的距离很小，与1个分子的直径相当。有外加电场作用时，带电质点和溶液中的反粒子分别向相反电极移动，产生电动现象。平板双电层理论虽然能解释一些电动现象，对早期的研究起了一定的作用，但却存在许多问题，如不能解释带电表面与溶液发生相对运动时移动边界与液体内部的电势差（ζ电势，又称电动电势）。

图1 Helmholtz双电层平板电容模型Fig.1 The Helmholtz double layer model

2.2.2 Gouy-Chapman扩散双电层模型

1910年左右，Gouy［16-17］和Chapman［18］先后提出了扩散双电层理论。他们认为靠近固体表面的反粒子不是整齐地排列在一个平面上，而是呈扩散状态分布在溶液中。这是因为反离子同时受到两个相反方向的作用力：静电引力与热运动的扩散作用。前者使其趋于靠近固体表面，后者使其趋于均匀分布在溶液中。这两种相互作用平衡后，反离子呈扩散状态分布，服从玻尔兹曼分布定律。距离固体表面反离子浓度越高，随距离增大，离子浓度逐渐下降。其模型如图2所示，固体表面带正电荷，吸引溶液中的反号离子。距表面一定距离处的电势与表面电势的关系用玻尔兹曼定律描述为

其中：κ的倒数具有双电层厚度的意义。

扩散层中的电势随距离增加而指数下降，下降的快慢取决于κ的大小。当离开固体表面足够远时，溶液中正负离子所带电量大小相等、符号相反，过剩的反离子浓度为零，此处对应的电势也为零。κ可以表示为

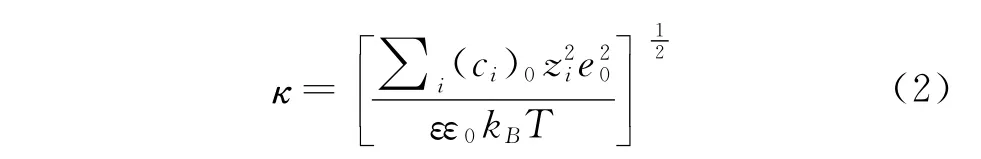
其中：（Ci）0为第i种离子的浓度；Zi为该离子对应的价态；e0为元电荷所带电量；ε为溶液的相对介电常数；ε0为真空中的介电常数；kB为波尔兹曼常数；T为绝对温度；k-1为具有长度的量纲，称为德拜长度。

Gouy-Chapman扩散双电层模型正确反映了反离子在溶液中扩散分布情况及电势变化，但没有考虑反离子的吸附作用。

图2 Gouy-Chapman扩散双电层模型Fig.2 The Gouy-Chapman diffuse model of the double layer

2.2.3 Stern双电层模型

1924年，Stern［19］提出了一种更加接近实际的双电层模型。他认为离子是有一定大小的，且离子与固体表面除了静电作用外，还有范德华吸引力。因此在靠近表面1～2个分子层厚的区域内，反离子由于受到强烈的吸引，会牢固地结合在表面，形成紧密的吸附层，称为Stern层或固定吸附层。其余反离子扩散地分布在溶液中，构成双电层的扩散部分。Stern层内电位是线性下降的（类似图1），而扩散层的电势则按指数形式降低（见图2）。

2.2.4 Grahame模型

1947年，Grahame［20］进一步发展了Stern模型：认为一些离子或中性物质如溶剂分子能进入到Stern层，而在固体表面吸附的为去溶剂化的离子，因此将Stern模型中的电层分为3层：内Helmholtz层（IHP）、外Helmholtz层（OHP）以及扩散层，如图3所示［20］。内Helmholtz层结构与Stern层一致，即由去溶剂化的离子构成，且内Helmholtz面穿过去溶剂化的离子中心；外Helmholtz层由一些溶剂化离子构成，且外Helmholtz面穿过这些溶剂化离子中心。在外Helmholtz层之外为扩散层。内Helmholtz层的电位呈线性下降，外Helmholtz层连同扩散层，其电位随距离按指数关系下降。Grahame的模型明确指出内Helmholtz面为Stern面（对应电势φσ），动电过程中滑动面为外Helmholtz面（对应zeta电势，ζ电势）。ζ电势的大小，反应胶粒表面的带电程度。ζ电势越高，带电越多，其滑动面与溶液之间电势差越大，扩散层越厚。当溶液中电解质浓度增加时，介质中反离子浓度增大，扩散层变薄，把更多的反粒子挤进滑动面内，使ζ电势在数值上变小。当电解质浓度足够大，可使ζ电势为零。

Grahame发展的Stern模型已较为成熟，使用广泛，能很好地解释各种动电现象，但对于双电层模型本身，仍然有一些新的观点提出。20世纪五六十年代，Bockris基于水分子的考虑对双电层模型进行了大量的研究工作，认为固体在水溶液界面处有极性水分子的参与［21］，并且发现水分子的存在对双电层的电容值有一定影响［22］。1963年，Bockris等［23］提出了考虑界面水分子结构的双电层模型（BDM模型），如图4所示［23］。在金属与水溶液界面处，内Helmholtz层由定向的水分子以及特性吸附的阴离子构成，外Helmholtz层（即图4中的Gouy面）由杂乱的水分子及水合阳离子构成，最外层为扩散层。现在，这种双电层模型也经常被使用。

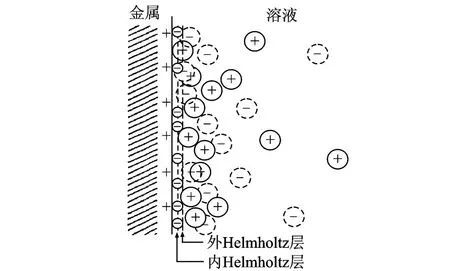
图3 Grahame模型Fig.3 The Grahame model

图4 BDM双电层模型Fig.4 The BDM model of the double layer

3 动电现象的分类及应用

动电现象自发现至今已有两百多年，在物理模型及数学公式的推导上取得了许多成果。Helmholtz［5］最早于1879年推导出了电渗流的数学表达式，但没有考虑溶液的介电常数。Smoluchowski［24］在1903年修正了Helmholtz的方程，即后来的Helmholtz-Smoluchowski公式。电泳、沉降电位、流动电势等动电现象的理论公式都是基于Helmholtz-Smoluchowski公式推演而来；但由于双电层是有厚度的，在微纳通道中还要考虑尺寸效应、溶液在受限环境中电导不同于体相溶液［25］、表面电荷密度的变化等。因此，在大多数情况下简单的公式无法完全描述微纳尺度的动电现象。在电动现象的应用方面，可以用于研究双电层的性质，根据理论公式推导出固液界面的ζ电势。流动电势、波动势及拽势等动电转换形式还可以应用于能量收集，尤其在微纳通道中具有较好的性能。

3.1 电泳和电渗

在外加电场作用下，离子或荷电粒子在分散介质中定向移动的现象，称为电泳。利用电泳现象可以测出粒子的ζ电势，反映粒子在溶液中的双电层性质。实验中通过测出一定时间内溶液界面移动距离，求得粒子的电泳速度，由电泳速度可以得出粒子的ζ势。介质中的粒子可以当成球形质点，当粒子半径较大，而双电层厚度较小，即κα≫1时，质点表面可以当成平面处理，此时可用Helmholtz-Smoluchowski公式描述电泳迁移率与ζ电势的关系

其中：ν为电泳速度；E为电场强度；μ为粒子的电迁移率，表示单位电场强度下的电泳速度；εr为介质的相对介电常数；ε0为真空介电常数；ζ表示zeta电位；η为介质的黏度。

当球形粒子半径较小，而双电层的厚度k-1较大，κα≪1，用Hückel-Onsager公式来描述电迁移率与ζ的关系

在水溶液中，一般很难满足κα≪1，通常水溶液中使用Smoluchowski公式。在一些非水系的溶液中，电解质浓度可降至极低，满足Hückel公式。

目前，毛细管中的电泳技术广泛应用于物质的高灵敏度检测及高效、快速分离。主要包括无机离子、糖类、氨基酸、蛋白质、DNA、环境样品、药物和食品等的分离分析［26-28］。其分离过程是基于样品中组分之间的淌度或分配系数的差异。混合物在电场条件下发生迁移过程中，各组分因自身性质不同，迁移速度不同，形成快慢不同的区带。时间越长，区带越小，数目越多，距离越开，即分离越好。各组分按其速度大小依次流出毛细管到达检测端，可以得到按时间分布的电泳谱图。在该电泳过程中，还伴随着溶液的电渗过程。当毛细管两端施加一定的电压后，荷电离子或粒子朝与电荷极性相反的电极方向移动。而毛细管内壁与溶液界面处形成双电层，双电层中的离子受电场作用会发生迁移，由于黏滞性的影响使得中性分子也跟着一起运动、迁移，形成电渗流。电渗流的流速特点是：管壁附近的流体流速最慢，远离壁面处流速快。流体截面流型为稳定的塞型状，而沿流道方向上均匀流动，即沿流道方向速度梯度为零。电渗流的表达式为

其中：QEO为电渗流流量；I为施加电场后的电流；KL为溶液的电导。

在一些纳米毛细管中，由于两边壁面双电层的重叠，式（6）［3］不再适用，而是与溶液中电势分布有关［29］。电渗流流速一般比电泳速度快5～7倍，因此毛细管电泳利用电渗流可将粒子朝特定方向推动。离子或荷电粒子的实际迁移速度是电泳和电渗流速度的矢量和。分散相粒子在重力场或离心力场的作用下迅速移动，在移动方向的两端产生电势差，即为沉降电位。沉降电位是电泳现象的反过程，理论公式可由Smoluchowski公式推导。

3.2 流动电势

3.2.1 流动电势的理论模型及数学表达

溶液在外力驱动下通过表面带电的毛细管壁或者多孔结构在两端会产生电势差，称为流动电势（流动电流）。其原理是流体受外力驱动，溶液与管壁间形成的双电层发生剪切运动，导致扩散层中的净电荷随着流动在某一端堆积，形成流动电流Istr并在两端产生电势差。该电势差形成的电场会使离子发生移动，产生一个反向电流Ic。稳定阶段，Istr= Ic，在外电路中测得的总电流为零。流动电流Istr可表示为移动电荷在单位时间内的积分，在不同的边界条件下有不同的表达式。

1）当κα≫1时，α表示毛细管半径（即管径恒大于双电层的扩散长度），可以运用Helmholtz-Smoluchowski方程，流动电流Istr表示为

其中：εr为液体的相对介电常数；ε0为真空介电常数；ζ为zeta电位；ΔP为两端压强差；η为液体黏度；Ac为管的横截面积；L为管长。

只要满足κα≫1，该式在多孔体系中也适用；但多孔介质不能简单近似为单管模型，因此管的横截面积Ac和管长L不易等效。在高浓度溶液中，双电层的厚度较小，不考虑双电层引起的表面电导对总电导的贡献时，实验上可以通过测体相溶液电导率，以及浸润溶液后多孔介质的电阻R∞，近似表达Ac/L［30］为

2）当κα值不大，如κα≈1～10，且ζ电势不高时，考虑曲率半径的效应，式（3）中将引入修正项，表示为

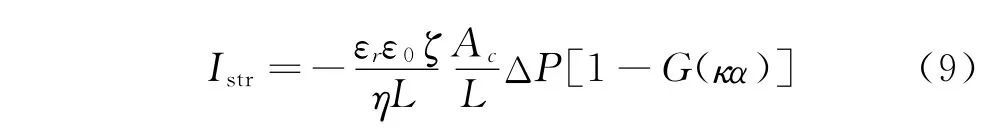
低浓度溶液中，当扩散层的厚度较大、表面电导Kσ对总电导贡献不能忽略时，Ustr表示为

对于狭缝状及管状的毛细通道，G（κα）有不同的表达，详见文献［31-32］。

3）当κα值很小，即双电层发生交叠，此时对应的溶液浓度较低，ζ势较高，Istr无法用简单的公式描述，只能采用数值方法。

在κα≫1条件下，流动电压可以通过公式描述。当不考虑双电层的表面电导对溶液总电导贡献时（如高浓度溶液中），Ustr表示为

3.2.2 微纳通道中的流动电势及应用

流动电势的研究涉及了众多的材料体系及结构。结构上包括平板表面、多孔介质以及柱形或矩形毛细微管等，研究者们发展了大量的理论模型来研究各结构及尺寸对流动电势产生的影响，其中微纳通道尤为复杂。研究的材料大部分为绝缘体，包括有机聚合物（如蚕丝、亚麻）和无机非金属化合物（如玻璃）等。在一些半导体和金属中也可以产生流动电势，并用来研究固液界面的双电层性质。Spanos等通过对半导体型的二氧化钛微球堆积的多孔介质测溶液的流动电位，计算出二氧化钛微球的ζ电势［33］。Giesbers等［34］用流动电势的方法测了金膜在溶液中的ζ电势以及双电层随溶液p H值的变化。液体在固体表面发生相对流动产生电势的现象，不仅用来表征固体与溶液界面的性质，测固体表面的ζ电势，还被应用于能量收集。单个微通道在1 k Pa压差下，产生的典型的流动电流值在纳安级。2003年，Yang等［35］首次提出了集成多个平行的微通道的理论模型，可以显著提高流动电流值。实验上实现了在60％孔隙率的多孔二氧化硅中在纯水或者低离子浓度的自来水条件下分别产生760 n A和1 500 n A的电流（单位压强产生的电流值达到0.5μA/k Pa）。van der Heyden等［36］报道溶液通过单个尺寸为4.5 mm长，500 nm高，50μm宽的矩形纳米通道时，在几百k Pa的压强差下可以产生高达4 V的开路电压。外接电路的最大输出功率可达到240 p W。Lu等［37］用含多个纳米孔阵列的氧化铝薄膜可以获得18 m W的输出功率，该输出功率足以驱动一些电子器件。能量转换过程中一个重要的评价指标为转换效率，Yang的实验中水静压力转换为流动电流的能量转换效率只有0.01％，van der Heyden实验中效率提高到3％。

图5 动电能量转换与浓度、尺寸、表面电荷密度的关系Fig.5 The relationship between the energy conversion efficiency and parameters of concentration，radius and surface charge

Daiguji等［38］通过理论计算表明当溶液浓度足够低，纳米通道的尺寸小于溶液德拜长度时，为了平衡表面电荷，在通道中溶液只带单种电荷，成为单极性液体。此时，可以产生大的电流和电压，提高转换效率。通过这种方式，选择特定浓度的溶液及通道尺寸，理论计算基于静水压转换为电能的效率能达到12％［39］。图5为流动电势能量转换效率与溶液浓度以及与腔道尺寸的关系［37］。一般来说流动电流、电势及效率随着浓度的增大而降低。在一些理论研究中也可以看到流动电流随浓度增大而增大的现象，如图6所示［40］。Dekker小组［40］通过理论计算表明，流动电流与浓度的关系分为3种情形：a.表面电荷σ一定，电势随浓度增高而降低；b.表面电荷不恒定（即有化学平衡参与），流动电势趋于随浓度增高而降低；c.ζ电势一定，流动电流随浓度增高而增高。但在实际的实验体系中只存在前两种情况：表面电荷恒定，或者表面电荷随溶液浓度变化而发生变化。情形（c）中ζ电势随溶液浓度受双电层厚度的影响不会恒定。效率随着表面电荷密度的增高而增高，与腔道尺寸的关系是非线性的。这是因为小腔道中双电层发生交叠，对运动的流体产生额外的排斥力，且当尺寸进一步减小时，电黏性增高，因此转换效率在某特定尺寸值以下将会降低。另一方面，当孔径逐渐增大并且高于德拜长度，腔道里不再是单极性的流体，由于异号离子的存在，Istr将会降低，导致整个效率的降低。除了上述改变溶液浓度及通道尺寸方式之外，Xie等［41］通过在腔道中引入气泡的方法形成气液双相流，降低Ic值，也可以提高输出功率以及转换效率。

图6 单位压强下的流动电流随溶液浓度的变化关系Fig.6 Streaming conductance as a function of KCl concentration for a nanochannel

3.3 拽势及波动势

3.3.1 拽势

在压力梯度下使液体在细小的通道或者孔洞中流动可以产生电势。对于纳米尺度材料来说，其对外部刺激的超强敏感性为实现高效能量转换提供了可能。最近，研究者通过将碳纳米管浸入到流动的液体中来发电［42］，但是这一流致生电现象及其机制存在着很多矛盾和争议［42-48］。另外，如何在没有压力梯度的情况下产生电势仍然是一个挑战。本研究团队发现当石墨烯置于一密闭管中，溶液在压力梯度下流经石墨烯表面且两端金属电极密封时，石墨烯两端并不产生电势差［49-50］；但是当穿过气液界面共存时，虽然石墨烯两端没有溶液压力差存在，但因气液界面沿石墨烯运动却产生了电压。例如，液体在石墨烯表面拖动或者波动都会产生电压。这与传统的流动电势的现象不同。本研究团队发现，这是双电压边界在石墨烯表面运动产生的新的动电效应：拽势［12］及波动势［13］。

图7为拽势的实验装置图［12］，大气环境下通过在一个单层石墨烯条带上拖动一滴海水或者含离子的水溶液会在其两端产生毫伏级的电压。液滴匀速运动时，电压信号在一常值附近小幅振荡，呈现方波形式，如图8（a）所示［12］。研究发现，电压和液滴的运动速度、液滴数目成正比，如图8（b）所示。根据这一线性关系，可以利用石墨烯来传感液滴运动的速度。

图7 实验装置示意图Fig.7 Illustration of the experimental set-up

图8 在石墨烯表面拖动一滴或多滴0.6 M氯化钠溶液产生的电压Fig.8 Voltage induced in graphene by drawing one or more droplets of 0.6 M NaCl solution

图9 拽势的机理解释Fig.9 Mechanism for the drawing potential

为了揭示该动电过程的本质，计算发现，浸入氯化钠溶液中的石墨烯表面会吸附一层水合钠离子。这一层水合钠离子导致石墨烯上下表面的电荷分离形成一双电层结构，构成赝电容，如图9所示［12］。液滴静止时，双电层结构对称，石墨烯两端电势相同，如图9（b）所示。当液滴运动时，液滴运动前端赝电容充电，尾端放电，导致石墨烯内形成一电势差，如图9（c）所示。这一动态过程可以由图9（d）和9（e）的等效电路表示。得到的结论和实验结果相吻合。多滴液滴的情况可以看作是多个这样的等效电路串联，如图9（f）所示。

基于该新的动电现象，本研究团队制备了一个书写识别装置，如图10（a）所示。在石墨烯片的4个边缘布置两对电极，通过分辨两对电极的电压信号来判断书写的笔画方向。图10（b）展示了沿4个方向书写时两对电极分别探测到的电压信号。此外，石墨烯中的动电效应在能量转化方面具有前景。如图10（c）所示，当一液滴落到斜放的石墨烯表面时，会在石墨烯两端产生高达25 m V的电压。

图10 拽势的应用Fig.10 Applications of the drawing potential

3.3.2 波动势

通过拽势的研究发现，液滴数量越多产生的电势越高。可通过溶液表面沿石墨烯来回波动，构建一个移动的气液边界会产生波动势［13］（图11（a）），电压值提高了一个量级。研究发现，该电势与运动速度以及浸入溶液的石墨烯长度成正比（图11（b））。

图11 石墨烯表面的海水波动势Fig.11 Waving potential in graphene moving across thesurface of seawater

系统的理论与实验研究揭示了波动势产生的原因：石墨烯插入溶液中时，液面处石墨烯吸附溶液中阳离子，而阴离子还来不及反应以屏蔽表面吸附的阳离子。这时石墨烯上部的电势比下部的电势高，导致石墨烯内部电荷的重新分布，在石墨烯内部形成电流，如图12（a）所示。本研究团队系统研究了其他溶液中石墨烯的波动势。与氯化钠溶液类似，石墨烯倾向于吸附溶液中的阳离子（图12（b））［13］。其他盐溶液中也能观察到与氯化钠溶液类似的波动势现象，但是去离子水例外（图12（c））。这是由于去离子水中缺乏离子的原因。值得注意的是，盐酸溶液中电压的极性与盐溶液的极性相反。这是由于酸溶液中氢离子会和石墨烯形成很强的物理吸附作用，氢离子不易脱附，从而吸附了一层氢离子的石墨烯在溶液中吸附阴离子，得到了和盐溶液相反的极性。当增加石墨烯插入溶液中的速度至1 m/s左右时，石墨烯两端的电压可达0.1 V。这一系列结果揭示了一种新奇的动电现象，并且为诸如海啸监视的多功能传感器提供了可能。

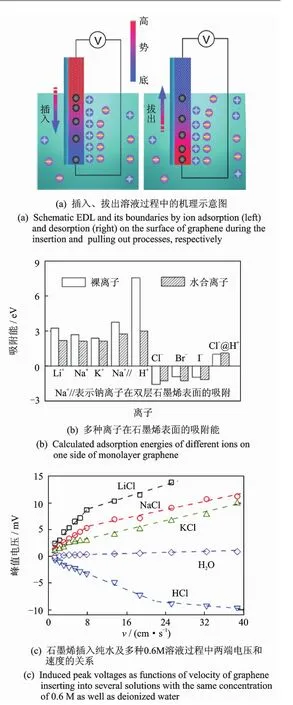
图12 石墨烯中的波动势Fig.12 Waving potential in a graphene sheet

4 总结与展望

目前，已知的动电现象主要包括：电泳、电渗、流动电位、沉降电位、离子振动电位、超声振动电位、扩散电泳、毛细渗透、拽势和波动势。基于动电效应的原理在科研实验中广泛应用于研究固液界面双电层结构。在工业生产如污水处理过程中，利用流动电势的方法能够迅速判断出污水处理的程度，降低处理成本。在油田开发中，了解动电现象能帮助判断开采过程中的一些问题，如压力异常、地层水淡化及多相流动等。另外，电泳、电渗现象还广泛应用于药物分析、生化分析、手性分离、环境分析和食品分析等领域。在能量转换、传感器件方面，基于动电效应的器件结构也有一定的应用前景。尤其在微纳系统中，由于尺寸效应的影响，流动电势的转换效率可以大幅提高；一些纳米材料如石墨烯对流体的超强敏感性为书写传感、海啸监测等方面提供可能。

［1］ Reuss F F.Sur un novel effet de l＇électricitégalvanique ［J］.Mémoires de la SociétéImpériale des Naturalistes de Moskou，1809，2：327-337.

［2］ Wiedemann G.Ueber die bewegung von flüssigkeiten im kreise der geschlossenen galvanischen säule［J］.Annalen der Physik，1852，87：321-352.

［3］ Wall S.The history of electrokinetic phenomena［J］.Current Opinion in Colloid＆amp；Interface Science，2010，15：119-124.

［4］ Quincke G.Ueber die fortführung materieller theilchen durch strömende elektricität［J］.Annalen der Physik，1861，113：513-598.

［5］ Helmholtz H.Studienüber electrische grenzschichten ［J］.Annalen der Physik，1879，7：337-382.

［6］ Dorn E.Ueber die fortführung der electricität durch strömendes wasser in röhren und verwandte erscheinungen［J］.Annalen der Physik Und Chemie，1880，10：46-77.

［7］ Debye P.A method for determination of the mass of electrolytic ions［J］.The Journal of Chemical Physics，1933，1：13-16.

［8］ Rutgers A J，Bemerkungen zu den von.Ultraschallwellen hervorgerufenen potential differenzen in lösungen［J］.Physica，1938，5：46.

［9］ Rutgers A J，Vidts J.Supersonic vibration potentials（debye effect）in colloidal solutions［J］.Nature，1950，165：109.

［10］Derjaguin B V，Sidorenko G P，Zubashchenko E A，et al.Kinetic phenomena in the boundary layers of liquids［J］.Kolloidn Zhurnal，1947，9：335-347.

［11］Derjaguin B V，Dukhin S S，Koptelova M M.Capillary osmosis through porous partitions and properties of boundary layers of solutions［J］.Journal of Colloid and Interface Science，1972，38：584-595.

［12］Yin Jun，Li Xuemei，Yu Jin，et al.Generating electricity by moving a droplet of ionic liquid along graphene［J］.Nature Nanotechnology，2014，9：378-383.

［13］Yin Jun，Zhang Zhuhua，Li Xuemei，et al.Waving potential in grapheme［J］.Nature Communications，2014，5：3582.

［14］Helmholtz H.Ueber einige gesetze der vertheilung elektrischer ströme in körperlichen leitern mit anwendung auf die thierisch-elektrischen versuche［J］.Annalen der Physik，1853，165：211-233.

［15］Damaskin B B，Petrii O A.Historical development of theories of the electrochemical double layer［J］.Journal of Solid State Electrochemistry，2011，15：1317-1334.

［16］Gouy L G.Sur la constitution de la chargeélectriqueà la surface d＇unélectrolyte［J］.Comptes Rendus Hebdomadaires des Seances de l＇Academie des Sciences，1909，149：654-657.

［17］Gouy L G.Sur la constitution de la chargeélectrique a la surface d＇unélectrolyte［J］.Journal of Theoretical and Applied Physics，1910，9：457-468.

［18］Chapman D L.A Contribution to the theory of electrocapillarity［J］.Philosophical Magazine，1913，25：475-481.

［19］Stern O.Zur theorie der electrolytischen doppelschicht ［J］.Zeitschr Für Elektrochemie，1924，30：508-516.

［20］Grahame D C.The electrical double layer and the theory of electrocapillarity［J］.Chemical Reviews，1947，41：441-501.

［21］Bockris J O M，Potter E C.The mechanism of hydrogen evolution at nickel cathodes in aqueous solutions ［J］.The Journal of Chemical Physics，1952，20：614-628.

［22］Bockris J O M，Conway B E.Determination of the faradaic impedance at solid electrodes and the electrodeposition of copper［J］.The Journal of Chemical Physics，1958，28：707-716.

［23］Bockris J O M，Devanthan M A V，Mueller K.On the structure of charged interfaces［J］.Proceedings of the Royal Society of London A：Mathematical，Physical and Engineering Sciences，1963，274：55-79.

［24］Smoluchowski M.Contributionàla théorie l＇endosmoseélectrique et de quelques phénomènes corrélatifs ［J］.Krak Anz，1903，6：182-199.

［25］Stein D，Kruithof M，Dekker C.Surface-charge-governed ion transport in nanofluidic channels［J］.Physical Review Letters，2004，93：035901.

［26］Yang H，Ding Y，Cao J，et al.Twenty-one years of microemulsion electrokinetic chromatography（1991-2012）：a powerful analytical tool［J］.Electrophoresis，2013，34：1273-1294.

［27］van Dorp S，Keyser U F，Dekker N H，et al.Origin of the electrophoretic force on DNA in solid-state nanopores［J］.Nature Physics，2009，5：347-351.

［28］Guttman A，Paulus A，Cohen A，et al.Use of complexing agents for selective separation in high-performance capillary electrophoresis：chiral resolution via cyclodextrins incorporated within polyacrylamide gel columns［J］.Journal of Chromatography，1988，448：41-53.

［29］Schoch R B，Han J，Renaud P.Transport phenomena in nanofluidics［J］.Reviews of Modern Physcis，2008，80：839-883.

［30］Delgado A V，González-Caballero F，Hunter R J，et al.Measurement and interpretation of electrokinetic phenomena［J］.Journal of Colloid and Interface Science，2007，309：194-224.

［31］Burgreen D，Nakache F R.Electrokinetic flow in ultrafine capillary slits［J］.Journal of Physical Chemistry，1964，68：1084-1091.

［32］Rice C L，Whitehead P.Electrokinetic flow in a narrow cylindrical capillary［J］.Journal of Physical Chemistry，1965，69：4017-4024.

［33］Spanos N，Koutsoukos P G.Calculation of zeta potential from electrokinetic measurements on titania plugs ［J］.Journal of Colloid and Interface Science，1999，214：85-90.

［34］Giesbers M，Kleijn J M，Cohen-Stuart M A.The electrical double layer on gold probed by electrokinetic and surface force measurements［J］.Journal of Colloid and Interface Science，2002，248：88-95.

［35］Yang J，Lu F Z，Kostiuk L W，et al.Electrokinetic microchannel battery by means of electrokinetic and microfluidic phenomena［J］.Journal of Micromechanics and Microengineering，2003，13：963-970.

［36］van der Heyden F H J，Bonthuis D J，Stein D，et al.Power generation by pressure-driven transport of Ions in nanofluidic channels［J］.Nano Letters，2007，7：1022-1025.

［37］Lu M C，Satyanarayana S，Karnik R，et al.A mechanical-electrokinetic battery using a nano-porous membrane［J］.Journal of Micromechanics and Microengineering，2006，16：667-675.

［38］Daiguji H，Yang P D，Szeri A J，et al.Electrochemomechanical energy conversion in nanofluidic channels ［J］.Nano Letters，2004，4：2315-2321.

［39］van der Heyden F H J，Bonthuis D J，Stein D，et al.Electrokinetic energy conversion efficiency in nanofluidic channels［J］.Nano Letters，2006，6：2232-2237.

［40］van der Heyden F H J，Stein D，Dekker C.Streaming currents in a single nanofluidic channel［J］.Physical Review Letters，2005，95：116104.

［41］Xie Y B，Sherwood J D，Shui L L，et al.Strong enhancement of streaming current power by application of two phase flow［J］.Lab on a Chip，2011，11：4006-4011.

［42］Ghosh S，Sood A K，Kumar N.Carbon nanotube flow sensors［J］.Science，2003，299：1042-1044.

［43］Zhao Y，Song L，Deng K，et al.Individual waterfilled single-walled carbon nanotubes as hydroelectric power converters［J］.Advanced Materials，2008，20：1772-1776.

［44］Liu J，Dai L，Baur J W.Multiwalled carbon nanotubes for flow-induced voltage generation［J］.Journal of Applied Physics，2007，101：064312.

［45］Král P，Shapiro M.Nanotube electron drag in flowing liquids［J］.Physical Review Letters，2001，86：131-134.

［46］Yuan Quanzi，Zhao Yapu.Hydroelectric voltage generation based on water-filled single-walled carbon nanotubes［J］.Journal of the American Chemical Society，2009，131：6374-6376.

［47］Persson B N，Tartaglino J U，Tosatti E，et al.Electronic friction and liquid-flow-induced voltage in nanotubes［J］.Physical Review B，2004，69：235410.

［48］Cohen A E.Carbon nanotubes provide a charge［J］.Science，2003，300：1235-1236.

［49］Dhiman P，Yavari F，Mi X，et al.Harvesting energy from water flow over graphene［J］.Nano Letters，2011，11：3123-3127.

［50］Yin Jun，Zhang Zhuhua，Li Xuemei，et al.Harvesting energy from water flow over graphene［J］.Nano Letters，2012，12：1736-1741.

O647；TM619

10.16450/j.cnki.issn.1004-6801.2015.04.001

郭万林，男，1960年10月生，教授、博士生导师。长期从事复杂环境下机械结构三维破坏理论及应用、飞机结构损伤容限与耐久性和纳米力学等研究。发表论文386篇，其中SCI收录252篇，被SCI他引3000余次。已申请中国发明专利16项，授权10项。1996年获国家杰出青年基金资助，1999年受聘教育部“长江学者奖励计划”特聘教授，2005年带领“纳尺度物理力学”团队入选教育部“长江学者创新团队”。2011年获教育部自然科学一等奖。2012年获国家自然科学二等奖和全国优秀科技工作者。2013年获徐芝纶力学奖。已培养25名博士，包括杰出青年基金获得者、青年千人、全国优博获得者和提名者等优秀人才。

E-mail：wlguo@nuaa.edu.cn

*国家重点基础研究发展计划（“九七三”计划）资助项目（2013CB932604，2012CB933403）；国家自然科学基金资助项目（51472117）；江苏省自然科学基金资助项目（BK20130781）；机械结构力学及控制国家重点实验室资助项目（0414K01）；中央高校基本科研业务费专项资金资助项目；江苏省研究生培养创新工程（KYLX-0224）；江苏高校优势学科建设工程资助项目（PAPD）

2015-07-24