改进的经验模式分解在机械故障诊断中的应用*

马文朋，张俊红，马 梁，刘 昱，贾晓杰（.天津大学内燃机燃烧学国家重点实验室 天津，300072）（2.天津理工大学机械工程学院 天津，300384）（3.天津大学仁爱学院 天津，30636）

改进的经验模式分解在机械故障诊断中的应用*

马文朋1，2，张俊红1，3，马 梁1，3，刘 昱1，贾晓杰1
（1.天津大学内燃机燃烧学国家重点实验室 天津，300072）
（2.天津理工大学机械工程学院 天津，300384）（3.天津大学仁爱学院 天津，301636）

针对经验模式分解（empirical mode decomposition，简称EMD）在工程应用中存在的端点效应和模式混叠问题，提出了一种改进的EMD方法。首先，利用遗传支持向量回归对短信号进行延拓；然后，采用改进的包络拟合方法并结合总体经验模式分解（ensemble empirical mode decomposition，简称EEMD）处理信号，数值仿真结果验证了该方法能够有效抑制端点效应和模式混叠；最后，利用该方法并结合包络解调对滚动轴承内圈故障信号进行实验与分析。结果表明，与EMD相比，该方法可以更有效地提取故障特征，满足机械设备故障诊断工程实际需求。

经验模式分解；端点效应；遗传支持向量回归；模式混叠；包络拟合；故障诊断

引 言

振动分析是机械设备故障诊断的重要技术手段，机械设备通常激励源较多，传递路径复杂，当故障发生发展时，其振动信号受故障的作用和多种激励的调制，一方面表现出非平稳、非线性特性，另一方面经多层传递后部分故障信息衰减较为严重，故障特征不明显。能否从非平稳振动信号中提取故障特征是机械故障诊断的关键。EMD及相应的Hilbert-Huang变换（Hilbert-Huang transform，简称H HT）［1］是一种非平稳、非线性信号分析方法，由于其良好的自适应性及优秀的时频分辨力，在机械故障诊断中得到了广泛应用［2-4］。虽然EMD，H HT比傅里叶变换和小波分析等有较大的优势，但EMD本质上是基于算法的方法，基础理论不完善，在实际应用中还存在一些问题，限制了其应用范围，其中比较突出的是端点效应和模式混叠问题。国内外学者针对这些问题进行了广泛研究，笔者将目前解决端点效应的主要方法总结为3类。

1）极值点延拓法包括多项式拟合延拓［5］、极值斜率延拓［3］和极值镜像延拓［6］等，其思想是在每次平滑时对信号极值进行延拓，为拟合上下包络线提供边界条件。该方法简单易行，但仅以信号端点处的极值点为依据，当信号波动较大时不能准确反映信号的趋势，极值点信息不准确。

2）信号时间序列延拓法包括波形匹配延拓［7］、波形镜像延拓［8］、神经网络预测［9］、自回归模型预测［10］、支持向量回归（support vector regression，简称SVR）预测［11］和最大Lyapunov指数预测［12］等。这类方法的思想是对待分解的信号时间序列进行延拓，再对延拓后的信号进行分解，将端点效应抑制在原序列之外，分解完成后舍弃延拓部分。该类方法可同时解决Hilbert变换时的端点效应问题，是当前较实用的方法，但上述几种方法也存在不足和待改进之处。波形匹配延拓适于处理周期或循环平稳信号，对于其他信号可能找不到匹配波形；波形镜像延拓对信号的对称性要求较高；神经网络的预测精度依赖于样本容量和网络结构，且容易陷入局部极小，实际应用中效果欠佳；自回归或时变自回归模型只适用于平稳信号或弱非平稳信号的延拓；基于SVR和最大Lyapunov指数的延拓方法表现出了较好的应用前景，但模型的参数还有待优化。

3）窗函数法［13］的思想是用合适的窗函数对信号加窗，将端点效应控制在信号两端，保证信号中部数据分解的正确性；但该方法同样会导致分解结果两端数据畸变，不适用于过短的信号。

EMD模式混叠现象有两类：a.由间歇信号、异常扰动等间断事件引起的模式混叠；b.分解频率相近或振幅比过低的信号时产生的模式混叠［14］。针对前者，Li等提出了间断检测［15］的方法，将信号中的间断成分剔除后再进行分解。Huang等［16］利用白噪声的统计特性，在EMD的基础上提出了总体经验模式分解方法，但该方法中参数的选取是个问题。第2类现象的解决方法主要有利用辅助信号［17］、改进包络拟合方法［18-21］结合其他方法对混叠分量进行后续处理［22］等。

通过对比分析，笔者认为采用改进的包络或均值拟合方法仅需对标准EMD算法进行稍许改变，继承了EMD自适应的优点，操作易行，但拟合方法的选择与设计是个难点。笔者采用遗传支持向量回归（genetic support vector regression，简称GSVR）方法对待分解信号进行延拓以克服端点效应，改进包络拟合方法并结合EEMD以改善模式混叠。通过数值仿真对改进的方法进行了验证，将其应用于轴承故障诊断，并对实验结果进行了分析。

1 改进的经验模式分解

1.1 基于GSVR的端点效应处理

支持向量机是建立在统计学习理论基础上的一种通用机器学习方法，在解决小样本、非线性和高维问题中有优势，具有良好的泛化能力。SVR的基本思想是采用一非线性映射将输入空间映射到高维空间，并在高维空间构建最优回归超平面，使所有样本到最优超平面的距离最小。

给定样本集D=｛（yi，xi），i=1，2，…，l｝；l为样本数；xi∈RN为输入值；N为输入空间维数；yi为输出值。令z=Φ（x）表示低维空间RN到高维空间Z的映射，SVR模型为

其中：ω为最优超平面的权系数向量；b为偏置。

最优超平面的求解归结为如下优化问题

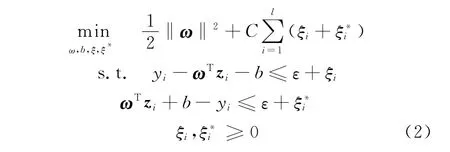
其中：C为惩罚因子，表示对样本偏离不敏感区域的惩罚程度，可看作对模型置信范围和经验风险的折中；ξ，ξ*为松弛因子，表示样本偏离不敏感区域的程度；ε为不敏感损失因子，表示允许的训练损失，可看作对解的稀疏性和回归精度的折中。

引入拉格朗日乘子α，α*，β，β*，将式（2）转化为拉格朗日对偶问题

根据极值条件求得minL（ω，b，ξ，ξ*，α，α*，β，

ω，b，ξ，ξ* β*）的最优解，将其带入式（4）和式（3），得到优化问题

引入核函数K（xi，xj）=zTizj，将高维空间的内积转化为低维空间的函数，大大降低了计算复杂度。由于径向基函数（radial basis function，简称RBF）良好的非线性映射能力和较少的参数，笔者选用RBF作为回归模型的核函数，RBF的形式为

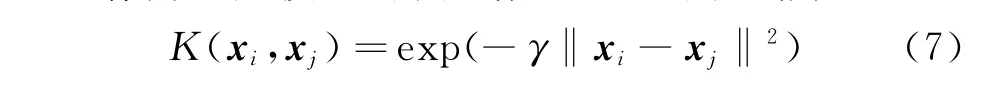
回归模型中参数C，ε，γ的大小对回归精度及模型的泛化能力有重要影响，笔者采用遗传算法以最小化交叉验证误差为准则对参数进行优化。交叉验证误差是泛化误差的一种近似无偏估计，通过交叉验证，样本中的所有样本点都被预测一次，准确率比较稳定。参数自适应优化过程如下：a.采用实数编码将C，ε，γ编制为染色体，设定搜索空间和种群规模，随机初始化种群；b.设定适应度函数f=1-E，E为训练样本交叉验证均方误差；c.采用比例选择、算数交叉和均匀变异算子，配合最优保存策略遗传进化，将末代最优个体解码获得最优参数。

利用GSVR对信号时间序列进行延拓以抑制端点效应，以向后延拓为例，按一定的规则产生训练样本集。给定信号序列S=｛s1，s2，…，sn｝，其中：n为采样点数；xi=｛si，si+1，…，si+m-1｝T为一训练样本点的输入；yi=si+m为输出；m（m＜n）为嵌入维数，一般取包含信号的若干个震荡即可。构造训练样本集T=｛（yi，xi），i=1，2，…，n-m｝，结合遗传

算法训练获得GSVR模型。利用该模型对样本点xn-m+1=｛sn-m+1，sn-m+2，…，sn｝T进行回归可得边界外的第1个延拓点sn+1，再将sn+1作为新的边界点再次构造样本进行回归可得第2个延拓点sn+2，依次类推，直至得到所需的延拓点数。要求延拓的信号至少要包含两个极值。向前延拓时，可将信号反向，再执行上述过程，延拓完成后再将延拓信号反向。

1.2 新型包络拟合方法

包络或均值的拟合方法影响着EMD的全过程，关系到迭代过程的收敛性，是EMD的关键问题之一，然而从理论上严格确定包络线仍是未解决的问题。标准EMD算法采用三次样条曲线分别对信号的极大、极小值进行插值获得上、下包络，然后对上、下包络求平均来拟合均值。由于三次样条曲线光滑有余，柔性不足，实际应用中易出现过冲或欠冲问题，影响分解的精度。同时，EMD分解双音信号时存在不可分区域［14］，当两信号的频率较为接近（0.67＜f1/f2＜1.5）或幅值比较小（A2/A1≤（f1/f2）2）时，将出现模式混叠乃至不可分。

一些学者提出改进包络拟合方法以提高拟合精度、扩大可分区域。Chen等［18］提出了基于B样条插值的均值拟合方法，可以准确逼近信号实际均值，但样条阶数的选择需人为确定。Qin等［19］提出了基于分段幂函数的包络拟合方法，可以兼顾曲线的光滑性与柔性，但存在参数的确定问题。Hong等［20］提出了基于局部积分平均的均值拟合方法，首先根据两相邻极值点间的曲线积分求得均值点，再用三次样条函数对均值点插值，但信号形式对结果准确性有重要影响，某些情况下与真实均值的差距较大。Xu等［21］提出了切触包络设计方法，从理论上证明了采用该包络进行迭代时，信号的包络波动会逐渐变小，最后收敛到恒包络信号，具有较高的理论意义和应用价值。鉴于此，笔者选用三次切触包络取代标准算法中的三次样条包络。

三次切触包络均值与通过式（8）定义的节点分段三次Hermite插值结果相同。

其中：s（ti）为信号的极值；ti为极值对应时刻；xm（ti），x＇m（ti）分别为信号包络均值及其一阶导数。

采用分段三次Hermite多项式对xm（ti）进行插值即可直接获得均值曲线。

1.3 改进算法的流程

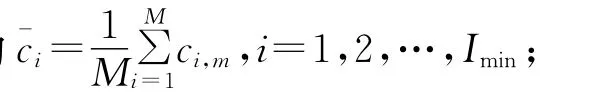
为尽量保证每次分解IMF的个数和特性相同，固定每个IMF的筛分次数为10。参数M和σ对分解结果有重要影响。过小的σ难以影响信号极值点的分布，不能解决模式混叠问题；σ过大又会破坏信号中高频成分的特性，会分解出多余的分量并使误差增大。M增大可以提高分解精度，但也会增加计算量。笔者依据文献［23］确定M和σ的取值。

2 数值仿真分析

进行仿真分析时，由于对仿真信号有足够的先验知识，为减少计算量，可仅对本研究方法的某一方面进行检验，也可对其整体效果进行验证。考察对短信号的处理能力，以经典非线性动力系统Duffing方程为例进行分析，无量纲Duffing方程的表达式为

其中：ε为非线性参数；γ，ω分别为控制函数的幅值和角频率，取ε=-1，γ=0.05，ω=0.5 rad/s。

采用Runge-Kutta方法进行求解，时间步长设为0.1 s，积分区间为［0，1 000s］，初值｛x（0）；x＇（0）｝=｛0.25；0｝，求得系统响应如图1所示。根据相轨迹和Poincare映射可知系统处于拟周期状态。结合极值镜像延拓对［100，200s］间的信号进行EMD及Hilbert变换，如图2（a），（b）所示。可见，IMF的端点和Hilbert谱的端点处都出现了明显失真。

图1 无量纲Duffing方程响应Fig.1 Responses of the dimensionless Duffing equation

采用笔者提出的GSVR模型对信号进行延拓，遗传算法的参数及回归模型的优化参数如表1所示。延拓结果如图3所示。延拓信号与真实信号基本吻合，得益于其优良的非线性映射能力，GSVR对拟周期信号也有较好的预测效果。对延拓后的信号进行EMD及Hilbert变换，结果如图2（c），（d）所示。对比图2（a），（b）可见，端点效应基本被消除，同时虚假IMF的波动与能量也显著减小。

表1 遗传算法参数及优化结果Tab.1 Parameters in genetic algorithm and the optimization results

为了考察对频率相近信号的分解能力，仍以Duffing方程为例，初值设为｛x（0）；x＇（0）｝=｛0.9；0｝，其他条件不变，系统响应如图4所示。依据幅值谱可知，系统非线性响应的特征频率f0≈0.117 2 Hz，ω/ω0≈0.679，分别采用改进的包络拟合方法（记为PE-EMD）和三次样条包络拟合方法（记为SE-EMD）对信号进行分解。对信号进行延拓、分解与Hilbert变换，如图5所示。SE-EMD分解结果中imf2的幅值远小于真实情况，imf1调频现象严重，且imf1与imf2的Hilbert谱出现了混叠。PEEMD分解结果中imf2的幅值和瞬时频率已基本接近真实值，imf1的调制现象相对减弱，同时也消除了混叠，这与实际情况比较吻合。

冲击和调制是机械设备故障信号常见的表现形式，笔者用一包含冲击和调制成分的信号来模拟故障信号s，其波形及组成如图6所示。s1～s3分别为冲击、调制和正常旋转成分。采用本研究方法（记为P-EEMD）对故障信号进行分解，设定加入噪声的标准差为0.04，总体平均次数为100，如7（a）所示。作为对比，采用PE-EMD进行的分解结果如图7（b）所示。可见，由于冲击信号这一间断事件的影响，PE-EMD的结果出现模式混叠并不断向后蔓延，各IMF丧失意义；P-EEMD的前3个IMF在误差允许范围内，与故障信号的3个成分基本对应，表现出了其优势，同时也说明了本研究方法可以应用于机械设备的故障诊断。

3 故障诊断实验与分析

图8为一深沟球轴承内圈故障的振动加速度信号［24］，信号具有明显的冲击与调制特性。轴承型号为SKF 6205-2RS，轴承内圈转速为1 752 r/mim，采样频率为12 k Hz，内圈故障特征频率约为158 Hz。采用本研究方法结合包络分析对故障信号进行处理。首先，对信号进行分解，如图9（a）所示；然后，对主要含高频冲击成分的第1个IMF求包络谱，如图9（b）所示，包络谱中明显可见故障特征频率fi及其倍频，其他比较明显的峰值为轴承旋转频率及其倍频。分解结果不够理想，前几阶IMF之间出项了轻微的混叠现象，这是由于信号中某些位置的冲击成分幅值过大且不对称，不满足成为IMF的条件，即使采用EEMD也不能完全消除模式混叠。采用EMD处理的结果如图9（c）所示，各IMF间出现了更为严重的模式混叠，冲击特征被分解至所有IMF中，这将导致故障特征不明显，第1个IMF的包络谱证明了这一点。可见，本研究方法的优越性得以验证，能够满足机械设备故障诊断工程实际的需求。

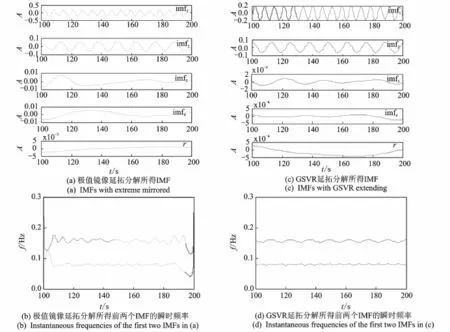
图2 EMD及Hilbert-Huang变换结果Fig.2 Results of EMD and HHT

图3 信号延拓结果Fig.3 Extension results of the signal

图4 系统响应的时间历程和幅值谱Fig.4 Time series and amplitude spectrum of the system response

4 结 论

1）针对EMD在工程应用中存在的两个突出问题，提出了解决方法，利用GSVR对短信号进行延拓以克服端点效应，同时采用切触包络代替三次样条包络并结合EEMD以抑制模式混叠。

图5 不同包络拟合方法的EMD分解结果Fig.5 EMD results with different envelope fitting algorithms

图6 模拟故障信号及其组成Fig.6 Fault signal simulated and its components

图7 模拟故障信号的EEMD与EMD分解结果Fig.7 EEMD and EMD results of the simulated fault signal

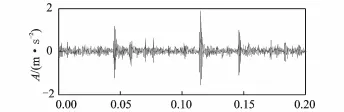
图8 轴承内圈故障信号Fig.8 Bearing signal with inner raceway defect

2）利用两个非线性信号和一个故障模拟信号对本研究方法进行了研究，并与标准EMD进行对比，验证了其有效性和优越性。

3）将本研究方法用于机械故障诊断，结合包络解调对轴承故障信号进行分析，结果表明该方法可以更准确提取故障特征。

图9 轴承故障信号的分解结果Fig.9 Decomposition results of the bearing fault signal

［1］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London，Series A，1998，454：903-995.

［2］ Lei Yaguo，Lin Jing，He Zhengjia，et al.A review on empirical mode decomposition in fault diagnosis of rotating machinery［J］.Mechanical Systems and Signal Processing，2013，35（1-2）：108-126.

［3］ Wu Fangji，Qu Liangsheng.An improved method for restraining the end effect in empirical mode decomposition and its applications to the fault diagnosis of large rotating machinery［J］.Journal of Sound and Vibration，2008，314（3-5）：586-602.

［4］ 张志刚，石晓辉，施全，等.基于改进EMD和谱峭度法滚动轴承故障特征提取［J］.振动、测试与诊断，2013，33（3）：478-482.Zhang Zhigang，Shi Xiaohui，Shi Quan，et al.Fault feature extraction of rolling element bearing based on improved EMD and spectrum kurtosis［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2013，33（3）：478-482.（in Chinese）

［5］ 刘慧婷，张旻，程家兴.基于多项式拟合算法的EMD端点问题的处理［J］.计算机工程与应用，2004（16）：84-86，100.Liu Huiting，Zhang Min，Cheng Jiaxing.Dealing with the end issue of EMD based on polynomial fitting algorithm［J］.Computer Engineering and Applications，2004（16）：84-86，100.（in Chinese）

［6］ Rilling G，Flandrin P，Goncalves P.On empirical mode decomposition and its algorithms［C］∥IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing（NSIP2003）.Grado，Italy：［s.n.］，2003：8-11.

［7］ 高强，段晨东，赵艳青，等.基于最大相关波形延拓的经验模式分解端点效应抑制方法［J］.振动与冲击，2013，32（2）：62-66.Gao Qiang，Duan Chendong，Zhao Yanqing，et al.A maximal correlation waveform extension method for end effects reduction of empirical mode decomposition［J］.Journal of Vibration and Shock，2013，32（2）：62-66.（in Chinese）

［8］ Zhao Jinping，Huang Daji.Mirror extending and circular spline function for empirical mode decomposition method ［J］.Journal of Zhejiang University：Science Edition，2001，2（3）：247-252.

［9］ Deng Yongyun，Wang Wei，Qian Chengchun，et al.Boundary-processing-technique in EMD method and Hilbert transform［J］.Chinese Science Bulletin，2001，46（11）：954-961.

［10］胡劲松，杨世锡.EMD方法基于AR模型预测的数据延拓与应用［J］.振动、测试与诊断，2007，27（2）：116-120.Hu Jinsong，Yang Shixi.AR model prediction-based EMD method and its application to data extension［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2007，27（2）：116-120.（in Chinese）

［11］Cheng Junsheng，Yu Dejie，Yang Yu.Application of support vector regression machines to the processing of end effects of Hilbert-Huang transform［J］.Mechanical Systems and Signal Processing，2007，21（3）：1197-1211.

［12］杨永锋，吴亚锋，任兴民，等.基于最大Lyapunov指数预测的EMD端点延拓［J］.物理学报，2009，58（6）：3742-3746.Yang Yongfeng，Wu Yafeng，Ren Xingmin，et al.The largest Lyapunov prediction method for the end issue of empirical mode decomposition［J］.Acta Physica Sinica，2009，58（6）：3742-3746.（in Chinese）

［13］Qi Keyu，He Zhengjia，Zi Yanyang.Cosine window-based boundary processing method for EMD and its application in rubbing fault diagnosis［J］.Mechanical Systems and Signal Processing，2007，21（7）：2750-2760.

［14］Feldman M.Analytical basics of the EMD：two harmonics decomposition［J］.Mechanical Systems and Signal Processing，2009，23（7）：2059-2071.

［15］Li Helong，Yang Lihua，Huang Daren.The study of intermittency test filtering character of Hilbert-Huang transform［J］.Mathematics and Computers in Simulation，2005，70（1）：22-32.

［16］Wu Z，Huang N E.Ensemble empirical mode decomposition：a noise-assisted data analysis method［J］.Advances in Adaptive Data Analysis，2009，1（1）：1-41.

［17］Deering R，Kaiser J F.The use of a masking signal to improve empirical mode decomposition［C］∥2005 IEEE International Conference on Acoustics，Speech，and Signal Processing.Philadelphia，United States：［s.n.］，2005：IV485-IV488.

［18］Chen Qiuhui，Huang N，Riemenschneider S，et al.A B-spline approach for empirical mode decomposition ［J］.Advances in Computational Mathematics，2006，24（1-4）：171-195.

［19］Qin Shuren，Zhong Youming.A new envelope algorithm of Hilbert-Huang transform［J］.Mechanical Systems and Signal Processing，2006，20（8）：1941-1952.

［20］Hong Hong，Wang Xinlong，Tao Zhiyong.Local integral mean-based sifting for empirical mode decomposition［J］.IEEE Signal Processing Letters，2009，16（10）：841-844.

［21］Xu Zhengguang，Huang Benxiong，Li Kewei.An alternative envelope approach for empirical mode decomposition［J］.Digital Signal Processing，2010，20（1）：77-84.

［22］Tang Baoping，Dong Shaojiang，Song Tao.Method for eliminating mode mixing of empirical mode decomposition based on the revised blind source separation ［J］.Signal Processing，2012，92（1）：248-258.

［23］Zhang Jian，Yan Ruqiang，Gao R X，et al.Performance enhancement of ensemble empirical mode decomposition［J］.Mechanical Systems and Signal Processing，2010，24（7）：2104-2123.

［24］Case Western Reserve University Bearing Data Center.Seeded Fault Test Data［EB/OL］.2007-11-27.http：∥www.eec-s.cwru.edu/laboratory/bearing/download.htm.

TH17；TP306+.3

10.16450/j.cnki.issn.1004-6801.2015.04.006

马文朋，男，1988年11月生，博士研究生。主要研究方向为转子系统振动信号处理和故障诊断。曾发表《Fault diagnosis model based on fuzzy support vector machine combined with weighted fuzzy clustering》（《Transactions of Tianjin University》2013，Vol.19，No.3）等论文。

E-mail：wenpengma@tju.edu.cn

*国家自然科学基金委员会与中国民用航空局联合资助项目（U1233201）

2013-09-13；

2013-12-05