联轴器不对中导致的车体振动研究*

2015-01-12石怀龙王建斌戴焕云邬平波西南交通大学牵引动力国家重点实验室成都610031

振动、测试与诊断 2015年4期

石怀龙，王建斌，戴焕云，邬平波（西南交通大学牵引动力国家重点实验室成都，610031）

联轴器不对中导致的车体振动研究*

石怀龙，王建斌，戴焕云，邬平波
（西南交通大学牵引动力国家重点实验室成都，610031）

地铁车辆在牵引和制动阶段车体地板出现异常振动，严重影响了车辆乘坐舒适性，通过理论分析和线路试验，确定引起异常振动的原因并提出解决方案。采用短时傅里叶变换法分析试验数据，得出电机2倍转频为地板振动激扰源。建立了由电机轴、弹性联轴节和小齿轮轴组成的传动系统数学模型，说明了联轴节不对中效应下的电机和小齿轮之间的振动关系，推导出小齿轮轴空间力矩输出表达式，表明不对中效应将激起电机偶数倍转频振动，并以2倍转频振动能量最大，理论上解释了试验结果，指出减小联轴节不对中量可降低振动。减小联轴节不对中量后再次进行试验的结果表明，电机2倍转频振动显著降低，车体振动均方根值和幅值分别降低了41％和53％，车体振动减小到正常车辆水平，理论分析和试验测试结果得到相互验证。

地铁；车体；联轴节；不对中

引言

牵引传动系统是动力转向架的重要组成部分，其性能直接关系到车辆运行安全性、稳定性和平稳性等。弹性联轴节是传动系统的重要组成之一，当车辆在牵引和制动阶段电机输出扭矩时，可吸收由于主动轴与从动轴轴线不对中效应产生的振动。旋转机械系统的异常振动多为系统轴线不对中、质量不平衡和结构部件松动等原因［1］。文献［2-3］研究了联轴节不对中效应下的系统振动，转子倍频为主要振动形式。文献［4-5］通过试验研究了不对中转子系统的振动特征，指出转子裂纹和刚度不对称等会产生2倍转频振动，提出全息频谱方法可用于故障识别。孙超等［6］分析了齿式联轴器存在不对中效应时的系统振动特性，发现故障特征频率为角频率的2倍，且激励力幅随载荷和不对中量的增加而增大。周云龙等［7］研究了不对中效应下的风机振动问题，指出联轴器不对中故障频率除了基频外，以2倍频为主，不对中引起的振动随负荷及转速的提高而加剧。梅庆等［8］通过理论和试验研究了联轴节动力特性，指出花键连接是影响其动力学特性的关键因素，并测得弹性体呈弯曲形态时系统的临界转速。赵广等［9］讨论了齿式联轴器不对中的建模方法，通过试验研究了各种不对中状态下轴系振动特征。Al-Hussain［10］分析了不对中效应对旋转机械系统稳定性的影响，指出增大弹性体刚度可提高系统稳定性。Sudhakar等［11］综述了联轴节不对中建模方法，研究了系统临界速度和稳定性的影响，讨论了不对中效应诊断方法。文献［12］采用理论分析、试验和仿真方法研究了弹性联轴节振动特性，新设计联轴节可降低2倍转频振动85％～89％。以上研究局限于振动特征及作用力传递关系，未考虑轨道车辆和线路之间的耦合振动特点。

针对车体地板异常振动问题，笔者将转子动力学理论应用到轨道车辆牵引传动系统振动特性分析中，开展了车体地板振动问题的理论分析和试验工作，提出解决方案并进行线路试验验证。

1 车体振动表现

车辆在施加牵引加速和制动减速阶段，动力转向架上方车体地板发生异常振动，影响乘坐舒适性，而同时刻其他动车车体地板、拖车车体地板则无该问题。针对该振动车辆设计线路试验，为方便结果对比，根据对照试验原则，测试一列编组中表现异常和正常的动车车体地板的振动加速度，采集车辆在一次完整的牵引、惰行、制动过程数据信号，试验多次重复进行。采用短时傅里叶变换（short-time Fourier transform，简称STFT）方法分析试验数据，获得随时间变化的振动时频谱分布图。图1为异常和正常车辆的车体地板垂向振动加速度STFT时频谱图。颜色表示能量分布，颜色最深区域对应振动主频［13］。可见，图1（a）中存在和车辆运行速度相关的频率成分，表明是该频率造成地板异常振动。

图1 车体地板垂向振动加速度STFT时频谱图Fig.1 STFT spectrum of vertical acceleration of floor

2 车辆振动测试

2.1 试验方案

由于只有动车车体出现异常振动，因此测试了牵引传动系统的振动情况。依照对比试验原则，分别测试了出现异常和正常车辆转向架的传动系统状态，测试方案相同。试验时车辆空载，在直线段进行且足够长，线路条件良好。试验过程中车辆以恒定加速度施加牵引至最高运行速度75 km/h（需35 s左右），然后惰行一段时间（约15 s），再持续施加制动至停车（约20 s），完整的一次试验时间为80 s左右。

图2为牵引传动系统主要组成，包括牵引电机、弹性联轴节和齿轮箱等。牵引电机输出力矩经弹性联轴节传递给齿轮箱内部小齿轮，通过大齿轮和小齿轮的相互啮合来驱动轮对使车辆行走。其中，牵引电机刚性联接于构架，齿轮箱小齿轮端箱体通过吊杆联接在构架上，可通过高度调整垫略微调节吊杆长短，从而控制电机轴和小齿轮轴的对中度，如图3所示。齿轮箱大齿轮端箱体采用抱轴式安装，由车轴承载其重量。试验中采集小齿轮处箱体振动加速度、齿轮箱吊杆动应力和车体地板振动加速度等，部分测点布置如图3所示。

图2 动力转向架牵引传动系统组成Fig.2 Composition of driven system of motor bogie

图3 齿轮箱加速度传感器布置Fig.3 Accelerator sensor mounted at the gearbox

2.2 数据分析

图4，5分别为异常振动车辆和正常车辆的试验结果，给出了齿轮箱吊杆动应力和小齿轮端箱体的垂向振动加速度的时频谱图。图4表明，当车辆在牵引和制动阶段，吊杆动应力和箱体加速度的主频分布随车速变化，与图1（a）所示的车体地板加速度频谱分布相同。由图5可知，在相同试验工况下，吊杆动应力和箱体加速度频谱未出现与速度相关的主频，振动幅值明显低于异常振动车辆，与图1（b）所示的车体地板振动频谱分布相同。通过对照试验结果可以说明，异常振动是由转向架传递到车体，当转向架无异常激扰时，车体振动表现正常。图4表明，造成异常振动的主频分布与车速基本成线性关系，即振动频率随着车速的提高而提高，振动能量也随着车速的提高而变大。当车速为75 km/h时，振动主频为110 Hz左右。为了说明异常振动的主频分布与车速之间的线性关系，根据传动系统的工作原理得到电机转速与车速之间的关系式为其中：v为车辆运行速度（m/s）；ω为牵引电机转动频率（Hz）；i为齿轮箱内部大小齿轮的传动比（7.69）；D为车轮直径（0.842 m）。

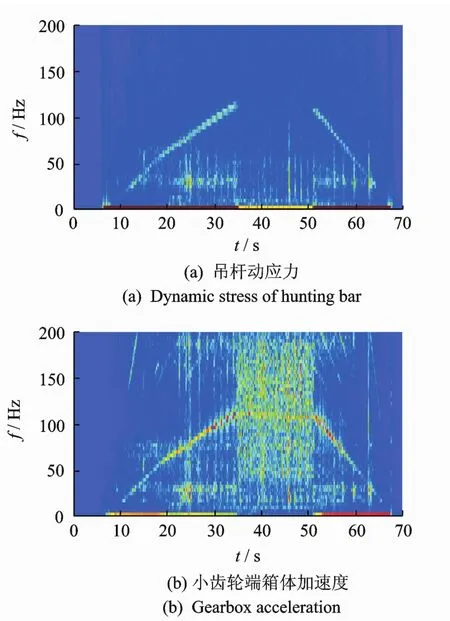
图4 异常车辆的实测信号STFT时频谱Fig.4 STFT spectrum of vertical acceleration of abnormal vehicle

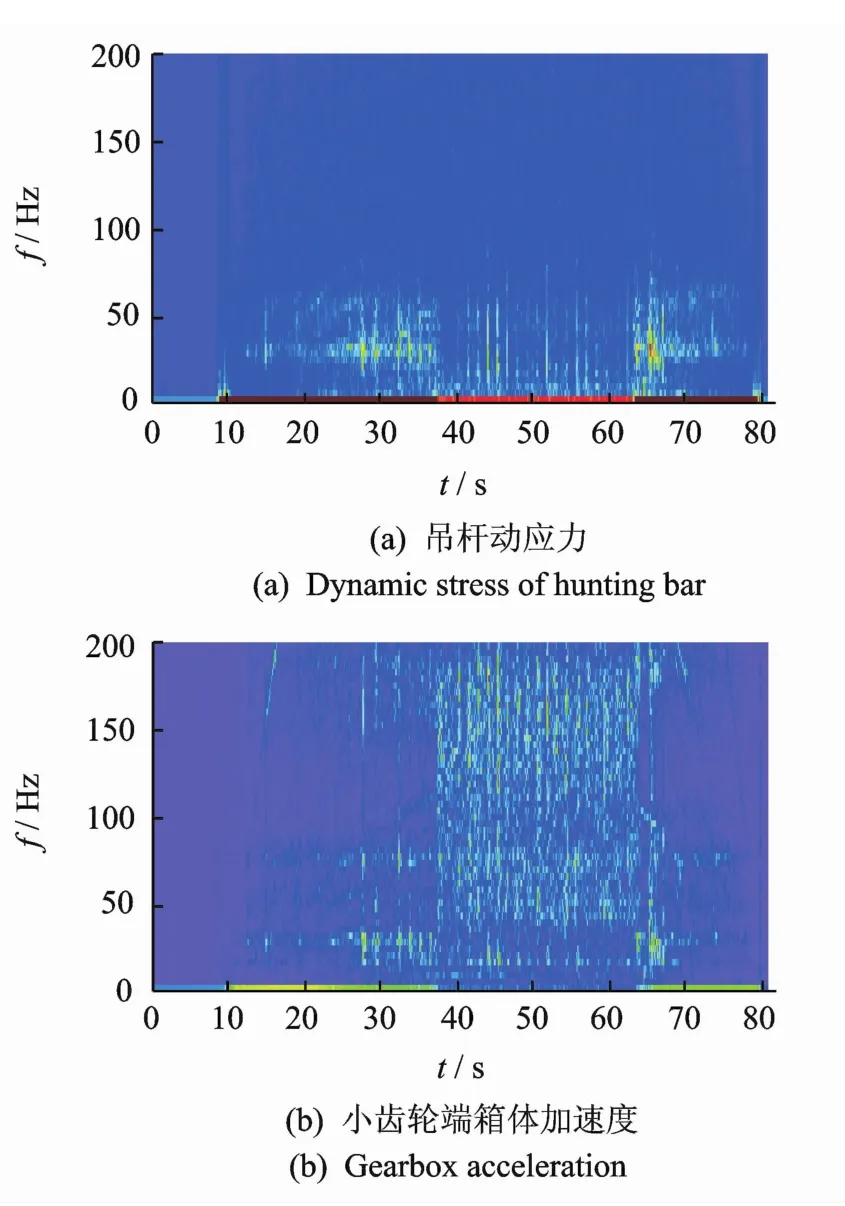
图5 正常车辆的实测信号STFT时频谱Fig.5 STFT spectrum of vertical acceleration of normal vehicle

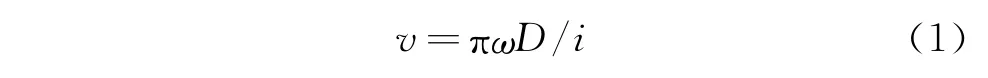
根据式（1）得到车辆在牵引、惰行和制动停车过程中电机转动频率随车速变化的关系曲线，如图6所示。当车速在0～75 km/h范围内，电机转频率ω变化范围为0～55 Hz，但其2倍频（2ω）变化范围为0～110 Hz，其他倍频频率变化范围更大。对比图6和图1，4的试验结果可知，2倍频振动与车体异常振动主频吻合，是车体地板异常振动的激扰源，而正常车辆则无此激扰源。

图6 电机转频与车速之间关系曲线Fig.6 The relations between the rotating frequency of motor and the running velociy of vehicle

3 联轴节振动特性

牵引电机、弹性联轴节和齿轮箱是牵引传动系统的重要组成，实现动力的产生、传递和输出功能。弹性联轴节是用于传递两相交轴扭转振动的一种空间低副机构，理论上两轴角速度相等，但由于联轴节效应等，当电机轴以角速度ωM匀速转动时，小齿轮轴的角速度ωR将按一定规律变化。建立包含牵引电机轴、弹性联轴节和小齿轮轴的传动系统数学模型，如图7所示。结合转子动力学理论分析联轴节振动特性［2-3］，电机轴输出力矩分解图如图8所示。模型考虑以下条件假设：a.考虑联轴节的角度不对中效应，考虑万向节效应，即采用角度不对中和电机空间位置来模拟角度不对中效应；b.将电机转动频率考虑定值，当出现不对中效应时电机输出力矩发生变化；c.将滚动轴承视为弹性支撑，忽略其阻尼和摩擦作用的影响。

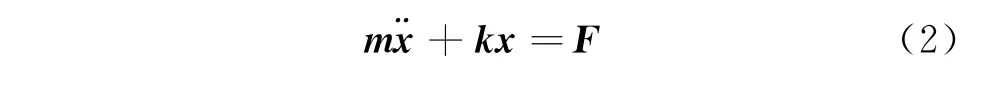
基于以上假设，由不对中引起的转动轴（电机轴或小齿轮轴）输出作用力方程为其中：m为转动轴的质量矩阵；k为转动轴的刚度矩阵；x为转动轴的输出位移向量；F为转动轴的输出作用力向量［10］。

图7中小齿轮轴沿坐标系x方向，电机轴沿直线AB方向，电机轴与小齿轮之间通过弹性联轴节来传递扭矩。α为电机轴与小齿轮轴间的夹角；β为电机轴与垂直于小齿轮轴平面间夹角；ωM为电机轴转动角速度；ωR为小齿轮轴转动角速度；θM为电机轴的角位移；θR为小齿轮轴的角位移。图8为电机轴输出扭矩分解图示。电机轴输出扭矩用T表示，沿x轴的分量用Tx表示，垂直于x轴的分量用Ts表示。

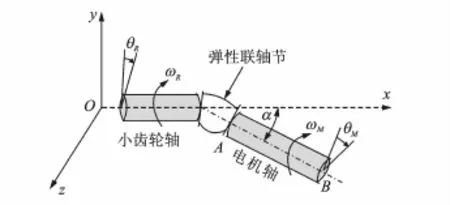
图7 联轴节角度不对中示意图Fig.7 Schematic diagram of the misalignment of flexible coupling

图8 联轴节输出力矩分解Fig.8 The decomposition of output torque of flexible coupling

小齿轮轴与电机轴间角速度［2］满足

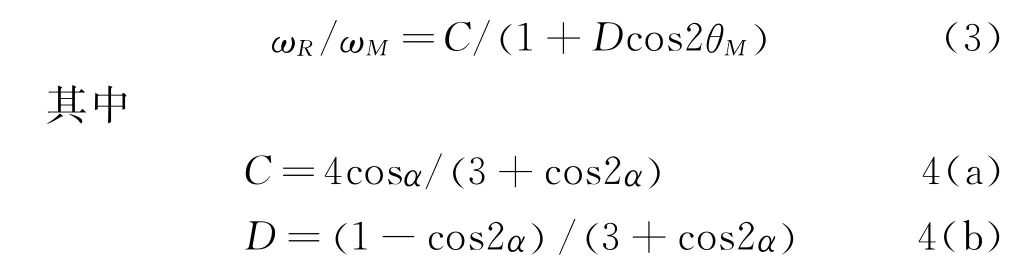
式（3）表明，弹性联轴节两侧的小齿轮轴与电机轴的转动角速度之比是变化的，即当电机轴等速转动时，小齿轮轴转速会随着两轴夹角的改变而发生变化，夹角越大，ωR变化范围就越大，说明小齿轮轴将产生角加速度，必然要引起动载荷作用而成为振动激扰源。

为了显示角速度之间的谐波特性和幅值大小关系，将式（3）展开

其中：n=1，2，3，…，且具有如下关系

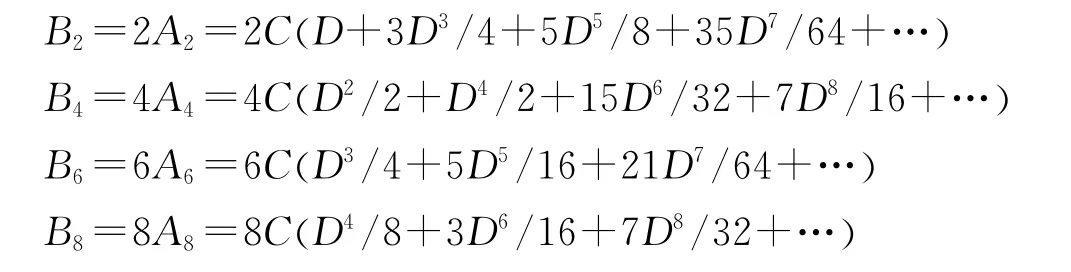
当小齿轮轴和电机轴完全对中时，两轴角速度应该相等，即ωR=ωM。此时α=0，有C=1，D=0，得到A0=1。小齿轮轴的角加速度可以通过式（5）对t进行微分得到

根据图8所示，电机输出扭矩通过弹性联轴节传递后可分解为两部分

其中：Tx为驱动小齿轮轴的转动扭矩；Ts作用于垂直小齿轮轴线方向（y-z平面），使小齿轮轴产生横向弯曲变形，激发垂直轴线方向上的振动。

将Ts在y，z坐标轴方向上分解

用Ix，Iy和Iz表示小齿轮轴相对坐标系的转动惯量，则小齿轮轴运动的欧拉方程可写为

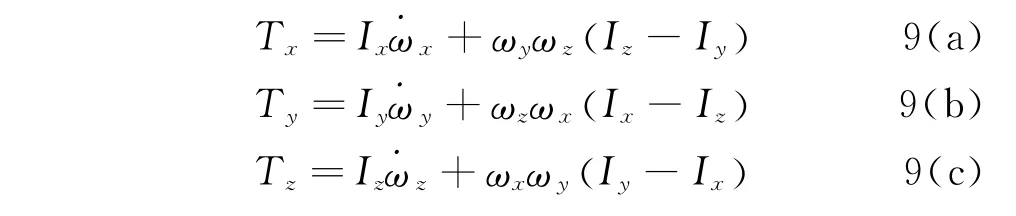
由于小齿轮轴只具有绕x轴旋转自由度，其欧拉方程可简写为

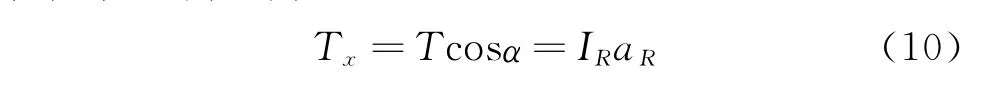
其中：IR为小齿轮轴相对于主轴线的转动惯量；aR为小齿轮轴的角加速度。

将小齿轮轴的角加速度式（6）代入式（10），得到小齿轮轴的扭矩方程解析式为

其中：θM=ωMt，t为时间变量。

式（11）表明，不对中产生的激振力频率为主动轴转速的偶数倍，并且以2X分量最大，4X，6X，8X等分量相比可忽略。根据强迫振动及共振的原理，不对中所引起的振动响应也将是以2X振动分量为主。

将式（11）代入式（8），可得小齿轮轴的弯矩振动方程为

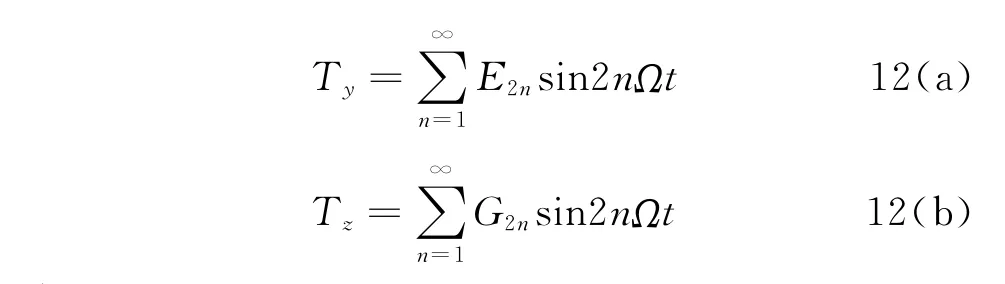
其中

上式表明由于弹性联轴节不对中效应将在小齿轮轴上产生弯矩作用，必然引起转动轴及系统的弯曲振动。将式（12）代入式（2），可得小齿轮轴的输出作用力向量表达式为）

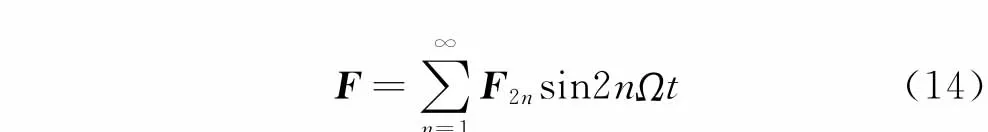
其中

式（12），（14）分别给出了当弹性联轴节存在不对中效应时，小齿轮轴的输出扭矩及作用力方程，表明其振动响应与不对中夹角α和电机位置β相关，振动频率为电机转速的偶数倍频率。

联轴节振动特性分析结果解释了试验分析结果，指出弹性联轴节不对中效应将产生电机的偶数倍转频激扰，其中2倍转频振动能量最大，传递至车体并成为地板异常振动的激扰源。根据理论分析结果可知，减小联轴节不对中量可减小该振动，通过调整联轴节不对中量可解决车体地板异常振动问题。

4 试验验证

为验证理论分析的可信性，在调整转向架联轴节不对中量后再次进行试验测试。通过调整齿轮箱吊杆的高度调整垫减少联轴节不对中量，如图9所示。分别测量并记录调整前后的联轴节两侧电机轴和小齿轮轴相对基准面的高度，测试结果见表1。其中：Hm为电机侧联轴节距离基准面高度；HR为小齿轮侧联轴节距离基准面高度；ΔH为联轴节高度差，ΔH=Hm-HR。由表1可知，相对于调整前，转向架的联轴节高度差减小了2～3 mm。

图9 测试联轴节不对中量Fig.9 Adjustment of misalignment amount

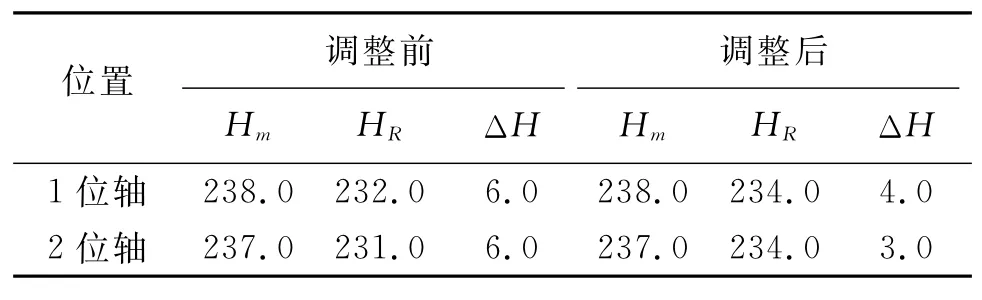
表1 联轴节不对中量调整结果Tab.1 Adjustment of misalignment amount mm

图10 调整后车体地板垂向振动STFT时频谱Fig.10 STFT spectrum of vertical acceleration of floor after reducing misalignment

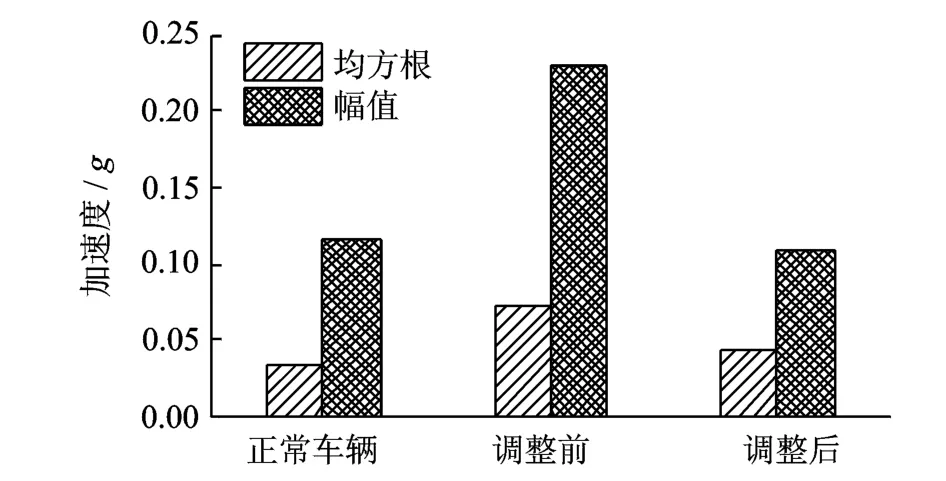
图11 车体地板振动水平对比Fig.11 Comparation of floor acceleration between the abnormal vehicle and misalignment adjusted vehicle

调整联轴节不对中量后再次进行试验，试验方案和调整前一致，测试结果如图10，11所示。对比图10和图1（a）所示的车体振动加速度频谱分布可知，减小联轴节不对中量后，电机2倍转频振动即异常振动激扰源的振动幅值显著降低，验证了理论分析结果。因吊杆动应力、小齿轮端箱体加速度和地板振动频谱分布一致，未列出具体结果。正常车辆和异常车辆调整前后的车体振动幅值对比如图11所示。结果表明，在减小联轴节不对中量后，车体振动加速度的均方根值、幅值均减小到正常车辆振动水平。调整前后振动加速度幅值对比表明，均方根值降低了41％，幅值降低了53％。

5 结论

1）试验结果表明，电机2倍转频为车体地板异常振动激扰源，正常车辆无该激扰源。

2）联轴节振动特性的理论分析表明，联轴节不对中效应将激起电机的偶数倍转频振动，并以2倍频振动能量最大，理论上解释了试验结果，并指出减小联轴节不对中量可以削弱该激扰。

3）验证试验结果表明，减小联轴节不对中量后电机2倍转频激扰振动减小，异常振动车体的振动激扰幅值显著降低。调整后的车体振动均方根值和幅值分别降低了41％和53％，振动减小到正常车辆水平，理论分析和试验测试结果得到相互验证。

［1］ Vance J，Zeidan F，Murphy B.Machinery vibration and rotordynamics［M］.Hoboken，New Jersey：John Wiley＆amp；Sons Inc.Publishers，2010：1-4.

［2］ Xu M，Marangoni R D.Vibration analysis of a motorflexible coupling-rotor system subject to misalignment and unbalance，partⅠ：theoretical model and analysis ［J］.Journal of Sound and Vibration，1994，176（5）：663-679.

［3］ Xu M，Marangoni R D.Vibration analysis of a motorflexible coupling-rotor system subject to misalignment and unbalance，part II：experimental validation［J］.Journal of Sound and Vibration，1994，176（5）：681-691.

［4］ Patel T H，Darpe A K.Experimental investigations on vibration response of misaligned rotors［J］.Mechanical Systems and Signal Processing，2009，23（7）：2236-2252.

［5］ Patel T H，Darpe A K.Vibration response of misaligned rotors［J］.Journal of Sound and Vibration，2009，325（3）：609-628.

［6］孙超，韩捷，关惠玲，等.齿式联轴器联接不对中振动机理及特征分析［J］.振动、测试与诊断，2004，24（3）：229-233.Sun Chao，Han Jie，Guan Huiling，et al.Analysis of force，motion and vibration of gear coupling with misalignment［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2004，24（3）：229-233.（in Chinese）

［7］周云龙，王锁斌，刘永奇.自回归和EMD用于离心式风机不对中故障分析［J］.振动、测试与诊断，2011，31（5）：582-585.Zhou Yunlong，Wang Suobin，Liu Yongqi.Application of EMD and auto-regressive model in centrifugal fan misalignment fault analysis［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2011，31（5）：582-585.（in Chinese）

［8］梅庆，力宁.弹性联轴器动力特性分析与实验研究［J］.振动与冲击，2008，27（6）：128-131.Mei Qing，Li Ning.Dynamic characteristics analysis and test of an elastic coupling［J］.Journal of Vibration and Shock，2008，27（6）：128-131.（in Chinese）

［9］赵广，刘占生，叶建槐.转子-不对中花键联轴器系统动力学特性研究［J］.振动与冲击，2009，28（3）：78-82.Zhao Guang，Liu Zhansheng，Ye Jianhuai.Research on dynamics of rotor-misaligned spline coupling system ［J］.Journal of Vibration and Shock，2009，28（3）：78-82.（in Chinese）

［10］Al-Hussain K M.Dynamic stability of two rigid rotors connected by a flexible coupling with angular misalignment［J］.Journal of Sound and Vibration，2003，266（1）：217-234.

［11］Sudhakar G N D S，Sekhar A S.Coupling misalignment in rotating machines：modelling，effects and monitoring［J］.Noise＆amp；Vibration Worldwide，2009，40（1）：17-39.

［12］Hariharan V，Srinivasan P S S.Vibration analysis of parallel misaligned shaft with ball bearing system［J］.Songklankarin Journal of Science and Technology，2011，33（1）：61-68.

［13］李舜酩，李香莲.振动信号的现代分析技术与应用［M］.北京：国防工业出版社，2008：110-113.