动态载荷位置识别当量载荷误差判别法*

2015-01-12姜金辉祝德春浦玉学南京航空航天大学机械结构力学及控制国家重点实验室南京210016南京航空航天大学振动工程研究所南京210016

振动、测试与诊断 2015年4期

蒋祺，张方，姜金辉，祝德春，徐菁，浦玉学（1.南京航空航天大学机械结构力学及控制国家重点实验室南京，210016）（2.南京航空航天大学振动工程研究所南京，210016）

动态载荷位置识别当量载荷误差判别法*

蒋祺1，2，张方1，2，姜金辉1，2，祝德春1，2，徐菁1，2，浦玉学1，2
（1.南京航空航天大学机械结构力学及控制国家重点实验室南京，210016）
（2.南京航空航天大学振动工程研究所南京，210016）

根据线弹性系统的振动特性，采用动载荷识别频域法研究动载荷作用位置识别问题。提出了当量载荷误差判别法，用不同测点响应在相同位置反演出来的当量载荷的误差值建立目标函数，当量载荷误差最小的作用位置就是动载荷的真实作用位置。从单点激励和两点激励方面进行了平面板的载荷位置识别仿真，在加入噪声的情况下效果依然理想，为复杂结构和多个加载位置动载荷识别提供基础。简支梁实验结果表明，该方法能正确识别载荷作用位置，对噪声不敏感，有很好的工程应用前景。

载荷识别；位置识别；当量载荷；频域法

引言

在结构动力学中，特别是在航空航天领域中，经常遇到结构承受的载荷不可预知和不好确定的问题。用一些分析方法和根据传感器测量的结果识别出未知载荷的位置和大小是结构健康状况评估、剩余寿命预测的前提。因此，载荷识别技术得到了快速发展。目前为止，动态载荷识别的频域法［1］和时域法已经比较成熟。动载荷识别是在已知载荷作用位置的前提下识别幅值的大小，一些新兴的（如小波［2］、人工神经网络和遗传算法等）智能算法被用于载荷识别。Choi等［3］提出了一种基于状态空间模型和最优平滑滤波同时识别冲击位置和重构载荷时间历程的方法，基于传统最优理论的反向求解器在识别和重构过程中引入了系统误差［4］。文献［5］对应用小波变换识别载荷位置作了尝试，通过对板的冲击特性分析，将不同频率弯曲波到达时间的确定方法与优化算法相结合，对冲击位置作了识别。文献［6-7］将遗传算法引入冲击载荷位置识别中，识别结果与实际情况有较好的一致性，表明了遗传算法在冲击载荷识别中具有良好的应用前景。文献［8］用级数展开方法研究了梁上动态载荷的位置及大小。文献［9］将壳体结构若干个点的挠度作为BP网络的输入量，通过3层神经网络结构输出载荷的位置。文献［10］利用有限元数值模拟与神经网络相结合的方法，研究了鸟撞实验中撞击力与撞击参数的获取方法，反演出撞击点坐标等撞击参数。文献［11］将神经网络和反向分析法相结合，提出了用于反求载荷位置和大小的有限元逆逼近方法，分别用于识别载荷位置和幅值大小。文献［12］利用压电智能夹层监测复合材料平板结构的动态响应，将响应信号的峰、谷值及到达时间等特征参数输入BP神经网络，识别冲击载荷的位置。文献［13］利用弹性平板结构上若干个观测点的弯曲挠度测量值，通过遗传算法进行迭代计算，识别出结构上载荷的作用位置。文献［14］提出了一种基于遗传算法的冲击载荷识别方法，将其应用于加筋复合材料结构的冲击载荷位置大小的识别，又提出了一种未知冲击时刻且缺失测量信息的情况下，同时识别冲击时刻和冲击位置并近似重构冲击载荷时间历程的方法［15］。文献［16］提出了一种通过性能参数稳定的光纤智能夹层采集数据，结合模糊RBF神经网络对飞行器机翼盒段载荷进行识别，有效识别出载荷的大小和作用位置。

以上研究位置识别的过程大多是铺设压电材料，或者需要知道结构的材料、边界条件以及结构中的波速等信息。笔者根据弹性元件的振动特性，采用动载荷识别频域法研究动载荷作用位置识别问题。提出了当量载荷误差判别法，从单点激励和两点激励方面为复杂结构和多个加载位置动载荷识别提供基础。

1 当量载荷误差判别法

根据振动理论可知，在物体上任一位置作用动载荷，在其他位置由这个载荷产生的振动响应是唯一确定的。对于分别作用在a点和b点两个点的简谐集中载荷Fa（ω）和Fb（ω），如果他们在同一测量点c产生的响应Xc（ω）相同，那么Fa（ω）和Fb（ω）互为当量载荷。对于一维梁任意一个测点a的响应，在整个梁长度上都能得到一个与位置有关的当量载荷分布函数Fa（x，ω）。对于定频激励稳态响应，当量载荷分布函数就是一个关于位置x的单值函数Fa（x）。对于单点激励，取两个响应测量点a点和b点，得到两个当量载荷分布函数Fa（x）和Fb（x）。在真实作用位置处，当量载荷等于真实载荷，真实载荷作用位置一定在两个当量载荷分布函数的交点处。

在物体上选取一点测量得到动响应，任选一个点作为激励点，根据频域法算出真实载荷的当量载荷。去除对称性的影响，只有当量动载荷对应的位置位于引起物体振动的载荷的真实作用位置处时，当量载荷等于真实载荷。对于单点激励单点加载的情况，在物体上选取两点的动响应，分别针对每一点的响应算出物体上任意点的当量动载荷。对于每个位置来说，根据两个点的动响应分别求出的当量动载荷不一定相等，只有在载荷的真实作用位置处，两个当量动载荷才是一致的。假设除了真实载荷作用位置以外，还有点的当量载荷是一致的，会出现如下情况。对于一组响应点m和n，当量载荷一致的载荷作用点为a和b，Fa（ω）和Fb（ω）为对应这组响应点在点a和b处的当量载荷，两个点的响应分别为Xm（ω）和Xn（ω），测点和激励点之间的传递函数为Ham（ω），Han（ω），Hbm（ω），Hbn（ω），满足以下关系

由式（3）和式（4）得

对于一组测点来说，如果有两处出现当量载荷对应相同，那么他们之间的传递函数应满足

通过用梁模型仿真，发现在频响函数矩阵中不存在相应的元素满足式（7），因此可以确定对于每个位置来说，根据两个点的动响应分别求出的当量动载荷不一定相等，只有在载荷的真实作用位置处，两个当量动载荷才是一致的。

在存在误差的情况下，在载荷真实的作用位置处，两个当量动载荷的幅值之差接近零。寻找动载荷加载部位的问题归结为两个测量的动响应在频域下是否满足下列附加条件矩阵

由式（8）可知，在物体上寻找一个虚拟激励位置i，使得在该处识别出的两组当量动载荷幅值之差趋向于零，此处就是动载荷的真实激励位置。在物体上假设一系列虚拟激励位置，用两组响应分别识别各虚拟激励位置处的当量动载荷，将两组当量动载荷幅值之差看做一优化函数，目标变量最小值对应的虚拟激励位置就是载荷的真实作用位置。这就是笔者提出的当量载荷误差判别法。

对于存在两点激励，假设是两个简谐集中载荷Fa（ω）和Fb（ω）。线性系统在任意点j的响应Xj（ω）必满足叠加原理

选择任意两个测点m和n的响应信息，可识别出一组虚拟动载荷

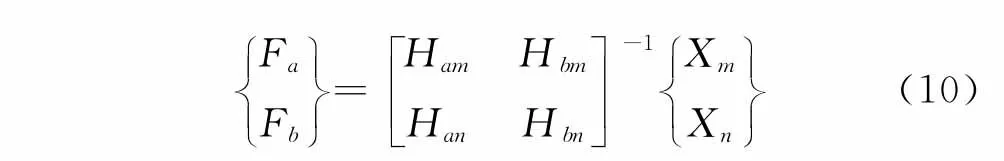
选取两个测点p和q的响应信息，可识别出另外一组虚拟动载荷

该层的主要设备是室内核心处理单元，它主要负责将感知控制层的各种传感器数据进行搜集，将终端发送来的数据转发给服务器或者向终端转发服务器的远程控制命令。

根据笔者提出的当量载荷误差判别法，满足下列附加条件时矩阵所对应的作用位置即为载荷的真实作用位置。

由此可拓展识别出物体受多个动态载荷激励情况下载荷的作用位置。

在有阻尼或相位差的情况下，式（1）可写成复数形式

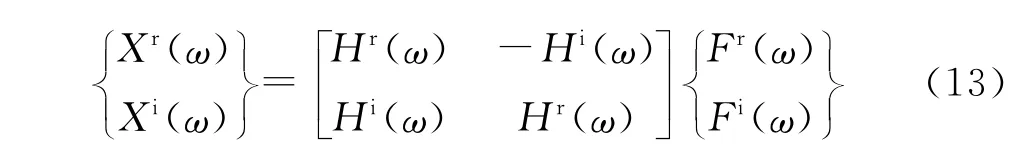
其中：上标r和i分别为相应物理量的实部和虚部。

当量载荷公式可以写成）

式（8）对应的目标函数公式为

2 仿真验证

2.1 仿真模型

一矩形四边简支板，板的长和宽均为l=1 m，厚度h=0.002 m，弹性模量E=720 GPa，泊松比μ=0.3，密度ρ=2 700 kg/m3。建立有限元模型，如图1所示。将该板划分为100个单元，共121个节点。由于四边简支，所以当量载荷作用点数目为81。

2.2 单点位置识别

在板上x=0.2 m，y=0.8 m处（对应节点号为91）作用一幅值为500 N、频率为52.5 Hz的正弦激励。选取板上x=0.6 m，y=0.5 m和x=0.4 m，y=0.7 m两处（对应节点号分别为62和82）的振动加速度响应谱用于识别，识别的当量载荷差值随节点变化曲线如图2所示。由图2可知，当量载荷差值最小点对应序号在81个虚拟激励位置排序为64。根据编程换算关系，该激励位置节点编号为91，与真实加载位置相同。

图1 薄板模型节点单元分布图Fig.1 Node and unit distribution of plate

为了进一步研究识别方法的抗噪声能力，在振动响应信号中添加10％的随机噪声，此时当量载荷差值随节点变化曲线如图3所示。由图3可知，当量载荷差值最小点对应序号在81个虚拟激励位置排序为64，根据编程换算关系，该激励位置节点编号为91，与真实加载位置相同。可以看出，当响应信号中混入随机噪声后，在载荷真实作用位置附近存在一些区域，使得在这些区域内识别的动态载荷与真实载荷较接近，但接近程度依然不及载荷真实作用位置处识别的值。

2.3 两点加载

在板上x=0.9 m，y=0.5 m处（对应节点号为65）作用一幅值为500 N，频率为52.5 Hz的正弦激励，x=0.7 m，y=0.7 m处（对应节点号为85）作用一幅值为500 N，频率为52.5 Hz的正弦激励。选取板上x=0.6 m，y=0.5 m，x=0.4 m，y=0.7 m 和x=0.7 m、y=0.2 m三处（对应节点号分别为62，82和30）的振动加速度响应谱用于识别，组合数为，识别的当量载荷差值随节点组合编号变化曲线如图4所示。

由图4并根据编程换算关系可知，当量载荷差值最小点对应的虚拟激励位置组合为64，85，与真实加载位置相同。

为了进一步研究识别方法的抗噪声能力，在振动响应信号中添加10％的随机噪声，此时当量载荷差值随节点组合编号变化曲线如图5所示。

由图5并根据编程换算关系可知，当量载荷差值最小点对应的虚拟激励位置组合为64，85，与真实加载位置相同。可以看出，当响应信号中混入随机噪声后，在载荷真实作用位置附近存在一些区域，使得在这些区域内，识别的动态载荷与真实载荷较接近，但接近程度依然不及载荷真实作用位置处识别的值。

图2 薄板单点识别当量载荷差值随节点变化曲线Fig.2 Equivalent load error cure changes with nodes（one load）

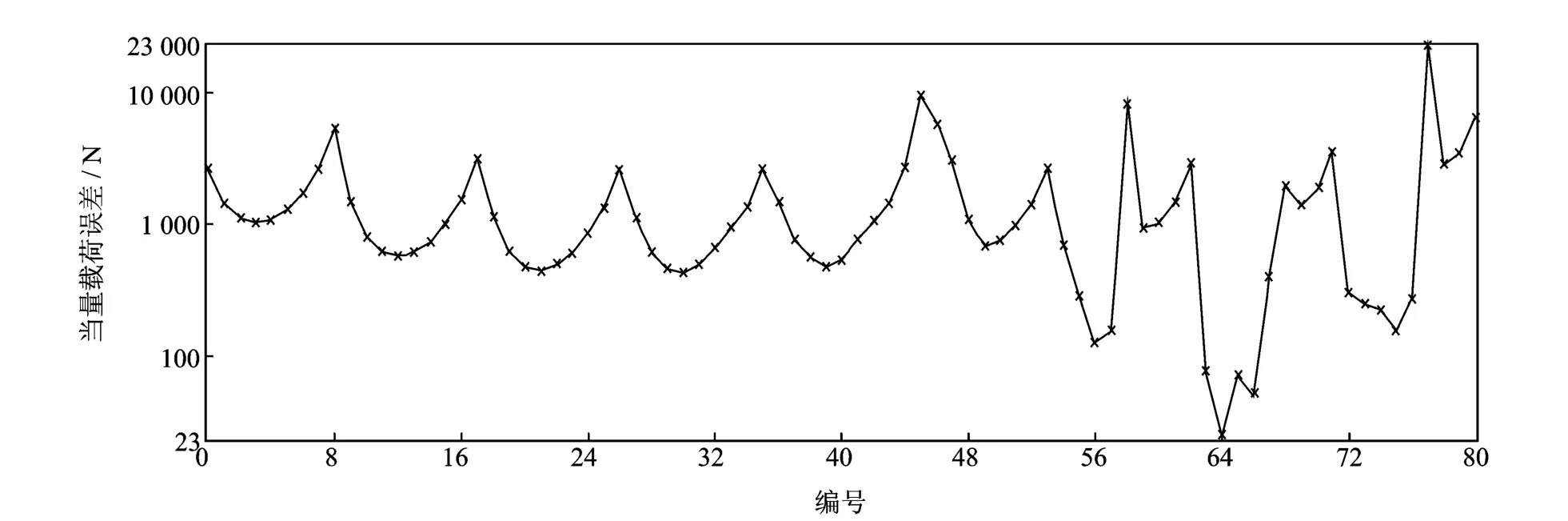
图3 薄板单点识别当量载荷差值随节点变化曲线（有噪声）Fig.3 Equivalent load error cure changes with nodes（one load，containing noise）

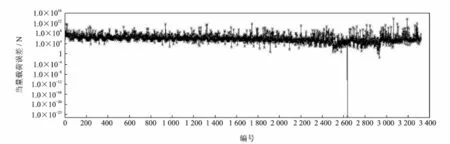
图4 薄板两点识别当量载荷差值随节点变化曲线Fig.4 Equivalent load error cure changes with nodes（two loads）

图5 薄板两点识别当量载荷差值随节点变化曲线（有噪声）Fig.5 Equivalent load error cure changes with nodes（two loads，containing noise）

3 实验验证

研究对象是两端简支梁，材料为铝合金，弹性模量E=70 GPa，泊松比μ=0.3，密度ρ=2 590 kg/m3，长l=0.68 m，横截面宽a=0.05 m，厚h= 0.008 m。整根梁分成9个单元，除去两铰支的端点外共8个节点。

用跑点法分别测出任意两个节点之间的传递函数，实际激励点在6号节点，选取节点2和节点5为一组测量点。激励频率为35 Hz，分别测出节点2和节点5频域下的响应，编程计算当量载荷差值随节点变化曲线如图6所示。由图可知，当量载荷差值ε最小值为0.000 117 565，对应6号节点，识别结果与真实载荷激励位置一致，成功识别出了载荷作用位置。

图6 两端简支梁当量载荷差值随节点变化曲线Fig.6 Equivalent load error cure changes with nodes on two ends simple supported beam

4 结束语

在频域法的基础上，将动载荷位置识别问题转化为目标函数求解最优化问题。仿真分析了单点激励和两点激励作用在简单板结构的情况，利用提出的当量载荷误差判别法进行了载荷位置识别，仿真结果理想。两端简支梁的实验表明，提出的当量载荷误差判别法简单实用，能够正确确定载荷作用的位置，对噪声不敏感，适用于多点加载的板壳结构。

笔者提出的位置识别方法是在载荷个数已知的情况下进行的。在载荷个数和位置都不知道的情况下进行载荷识别还有待于进一步研究。

［1］姜金辉，张方，陈寅.基于固有振型的复杂结构分布动载荷时域识别［J］.振动、测试与诊断，2012，32（4）：581-585.Jiang Jinhui，Zhang Fang，Chen Yin.Distributional load identification in time domain with the mode shape polynomial for complex structures［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（4）：581-585.（in Chinese）

［2］秦远田.分布动载荷识别的二维小波-伽辽金方法［J］.振动、测试与诊断，2012，32（6）：1005-1009.Qin Yuantian.A two-dimension wavelet-Calerkin method：distributed load identification［J］.Journal of Vibration，Measurement＆amp；Diagnosis，2012，32（6）：1005-1009.（in Chinese）

［3］ Choi K，Chang F K.Identification of impact force and location using distributed sensors［J］.American Institute of Aeronautics and Astronautics，1996，34（1）：136-142.

［4］章继峰，张博明，杜善义.最优化方法在动载荷时程重构中的应用研究［J］.振动与冲击，2006，25（4）：5-7.Zhang Jifeng，Zhang Boming，Du Shanyi.Application of optmization method to kinetic loading time history reconstruction［J］.Journal of Vibration and Shock，2006，25（4）：5-7.（in Chinese）

［5］ Gaul L，Hurlebaus S.Identification of the impact location on a plate using wavelets［J］.Mechanical Systems and Signal Processing，1997，12（6）：783-795.

［6］ Woeden K，Staszewski W J.Impact location and quantification on a composite panel using neural networks and a genetic algorithm［J］.Strain，2000，36（1）：61-70.

［7］ Haywood J，Coverley P T，Staszewski W J，et al.An automatic impact for a composite panel employing smart sensor technology［J］.Smart Material and Structures，2005，14（1）：265-271.

［8］王猛，王养丽.一种结构载荷识别的技术展开法［J］.华北电力大学学报，2001，28（3）：77-79.Wang Meng，Wang Yangli.Identification of structure loading using series expansion［J］.Journal of North China Electric Power University，2001，28（3）：77-79.（in Chinese）

［9］尚钢，吴代华.基于神经网络对扁壳结构载荷位置识别问题的研究［J］.固体力学学报，2001，22（1）：61-63.Shang Gang，Wu Daihua.Research on the identification of load location of shallow shell structures based on neural network［J］.Acta Mechanica Solida Sinica，2001，22（1）：61-63.（in Chinese）

［10］白金泽.基于神经网络方法的鸟撞飞机风挡反问题研究［D］.西安：西北工业大学，2003.

［11］周晚林，王鑫伟，胡自立.压电智能结构载荷识别方法研究［J］.力学学报，2004，36（4）：491-495.Zhou Wanlin，Wang Xinwei，Hu Zili.On load identification for piezoelectric smart structures［J］.Acta Mechanica Solida Sinica，2004，36（4）：491-495.（in Chinese）

［12］Haywood J，Coverley P T，Staszewski W J，et al.An automatic impact monitor for a composite panel employing smart sensor technology［J］.Smart Mater Struct，2005（14）：265-271.

［13］姜忠宇，孙建忠，赵常要.弹性薄板载荷反问题分析［J］.安徽工程科技学院学报，2006，21（1）：61-63.Jiang Zhongyu，Sun Jianzhong，Zhao Changyao.Analysis of elastic sheet＇s load inverse problem［J］.Journal of Anhui University of Technology and Science，2006，21（1）：61-63.（in Chinese）

［14］严刚，周丽.加筋复合材料结构的冲击载荷识别［J］.航空学报，2008，29（5）：1150-1156.Yan Gang，Zhou Li.Impact load identification for stiffened composite structure［J］.Acta Aeronautica et Astronautica Sinica，2008，29（5）：1150-1156.（in Chinese）

［15］严刚，周丽.冲击时刻未知情况下复合材料结构冲击载荷识别［J］.中国机械工程，2009，20（1）：99-103.Yan Gang，Zhou Li.Impact identification for composite structure with unknown impact time［J］.China Mechanical Engineering，2009，20（1）：99-103.（in Chinese）

［16］胡兴柳，梁大开，陆观.基于光纤智能夹层和模糊RBF神经网络的飞行器载荷识别［J］.南京航空航天大学学报，2009，41（4）：491-495.Hu Xingliu，Liang Dakai，Lu Guan.Aircraft load identification based on smart layer of fiber and fuzzy RBF neural network［J］.Journal of Nanjing University of Aeronautics and Astronautics，2009，41（4）：491-495.（in Chinese）