中心极限定理在统计推断中的应用

丁 健，李红菊

(安徽新华学院公共课教学部，安徽合肥230088)

在经济数学的实际问题中，随机变量到处可见，许多随机变量服从正态分布，即使有些随机变量不服从正态分布，但它们的和也近似服从正态分布，这是由中心极限定理决定的.在概率论中凡是在一定条件下判定随机变量之和的分布是正态分布的定理统称为中心极限定理.中心极限定理解释了正态分布广泛存在的原因，并为解决实际问题时利用正态分布提出了理论依据.目前教科书上仅对中心极限定理做了理论上的阐述，对它的实用价值涉及较少，本文通过统计推断中的实际问题来说明中心极限定理的广泛应用.通过对实际问题的探讨和学习，学生能够较深刻地理解和掌握中心极限定理，这对教学有实际意义.

1 中心极限定理

独立同分布的中心极限定理和棣莫弗－拉普拉斯中心极限定理是我们所熟悉的两大类中心极限定理，具体内容如下:

独立同分布的中心极限定理［1］设随机变量 X1，X2，…，Xn相互独立，且服从同一分布，E(Xi)=u，D(Xi)= σ2，i=1，2，…，n，则当 n 很大时，随机变量，即

棣莫弗 －拉普拉斯中心极限定理［1］在n重伯努力试验中，事件A在每次试验中发生的概率为p，ηn为事件A发生的次数，则当n充分大时，有或

2 中心极限定理的实际应用

2.1 中心极限定理在统计估计中的应用

数理统计一般研究正态总体均值和方差的统计估计，而由简单随机抽样得到的随机变量是相互独立且服从同一分布的，所以在实际问题中，不论总体服从什么样的分布，只要样本的容量充分大，我们就可以根据中心极限定理把随机变量的和近似看成服从正态分布，直接利用中心极限定理进行统计推断，对总体中未知参数进行区间估计.

不论总体服从什么分布，只要选择的样本容量足够大，根据中心极限定理，样本均值为选取枢轴量关于总体均值的置信水平为1－α的置信区间为在许多实际问题中，我们还经常碰到总体分布和总体方差均未知的情况，此时可以用样本方差s2作为总体方差D(X)的无偏估计量，用s2代替D(X)，根据中心极限定理，仍可以求出μ的置信水平为1－α的置信区间

例1 以X表示某一工厂生产的某种器材的寿命(以小时计)，经验表明D(X)=1156，现从总体中取得一容量为49的样本，得到各个观察值，并计算出样本均值珋x=1589，样本方差s2=1122.25.求总体均值μ在置信水平为0.95时的置信区间.

解 由题意可知，从总体中抽取了一个大样本(n=49)，不论总体服从什么样的分布，根据中心极限定理，样本均值

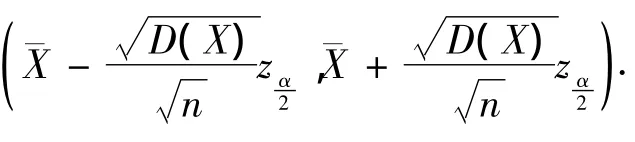
1－α=0.95，总体均值μ的置信水平为0.95的置信区间为查正态分布表得.代入观察值得到这家工厂制造的器件平均寿命的置信水平为0.95的置信区间为(1579.48，1598.52)，这说明这家工厂制造的器件平均寿命在(1579.48，1598.52)的概率不小于0.95.

注 如果在例1中不知总体的方差，仍可以计算出总体均值μ的置信水平为0.95的置信区间

如果试验是伯努力试验，随机事件A发生的概率p未知，可以从总体中抽取一个容量(n)很大的样本，fn表示事件A发生的次数。当样本容量很大时，二项式分布近似于正态分布，即)，对 p进行统计估计，则关于p的置信水平为1－α的置信区间为

例2 粮站有一大批粮种，欲了解粮种的发芽率p，在其中任选了6400粒进行试验，试验结果5000粒发芽，求粮种发芽率p的置信水平为0.99的置信区间.

1－α=0.99，得到发芽率p在置信水平为0.99时的置信区间为

2.2 中心极限定理在假设检验中的应用

假设检验是统计推断的另一个重要内容.对总体分布函数的形式或关于总体参数值的陈述叫做统计假设［1］.总体的分布或参数未知的情况下，通过一些预知的知识对总体提出两个假设H0和H1，然后根据样本去判断是接受H0还是拒绝H0的过程是假设检验［1］.

在许多实际经济问题中，研究的几乎都是大样本．根据中心极限定理，当样本容量很大时，对总体的均值进行假设检验，提出原假设 H0:E(X)=μ0，可以选取检验统计量或，当原假设H0成立时，检验统计量Z近～似N(0，1)，选择显著性水平为α，此时H0的拒绝域为

例3 某农业大学研究在改善栽培条件下黄豆的重量是否有明显改变，已知改善条件前黄豆的平均重量μ0=350(单位:mg)，σ未知，现随机地抽取100粒，测得这100粒黄豆的平均重量x珋=352.5mg，s2=25，问在显著性水平α=0.05条件下改善栽培条件后黄豆的重量是否较之前重量有明显差异?

解 由题意H0:E(X)= μ0;H1:E(X)≠μ0，其中μ0=350.

在显著性水平 α=0.05的条件下，H0的拒绝域为|Z|≤zα=Z0.025.

查正态分布表z0.025=1.96，故|Z|=，所以接受原假设，即认为在显著性水平α=0.05的条件下改善栽培条件后黄豆的重量较之前重量有明显差异.

3 结语

由于实际的经济问题均通过大样本来估计总体，总体的分布已知不是必要的解题条件，只要当样本容量很大，随机变量的和总是近似服从正态分布，正是这个结论使得中心极限定理可以解决很多实际问题.本文仅探讨了中心极限定理在统计推断中关于总体未知参数的区间估计和假设检验的一些实际应用，其实在商业管理决策、函数极限求法、保险业、抽样推断中的概率预测和样本容量的确定等实际问题中都会用到中心极限定理，所以对于中心极限定理的研究具有一定的理论意义和实际价值.

［1］盛骤，谢式千.概率论与数理统计及其应用［M］.北京:高等教育出版社，2010.

［2］刘家琨.应用概率统计［M］.北京:科学出版社，2004.