矩形晶格结构对二维固-液体系声子晶体能带结构的影响*

陶巧， 黄鉴， 王荣丽, 杨海

(1.云南师范大学 物理与电子信息学院，云南 昆明 650092；2.昆明学院 物理科学与技术系，云南 昆明 650214)

1 前 言

声子晶体的研究是在传统晶体和光子晶体研究的基础上提出的新课题，类比电子的De Broglie波和光波在周期结构中传播会产生频率带结构，人们设想弹性波(声波)在周期性结构中传播时也可能出现能带结构.1992年Sigalas和Economou[1]第一次在理论上得到了球形散射体埋入基体材料中形成的3D结构具有声子带隙.随后，Kuswhhaa[2]等人明确提出声子晶体的概念，并采用平面波计算方法对2D镍柱形成的复合材料进行计算，得到了声波带隙.声子晶体因其丰富的物理内涵和极其广阔的应用前景，引起了各国学者的高度关注[3-9].已有研究发现，当弹性波频率落在禁带范围内时，弹性波将被完全反射.因此，可通过对声子晶体的周期性结构及弹性参数进行调制，设计出不同的带隙结构，进而制造相应的隔音减振材料或新型的声学器件(如声波滤波器、声波导、声学透镜等)[10-14]，在军事上实现超声隐身，民事上实现用本来能透过声音的普通材料复合成高效率的隔音材料.

本文通过改变声子晶体晶格结构和填充率，研究其对声子带隙的影响.

2 理论

利用多重散射理论对各类声子晶体的计算都相当成功，其最突出的优点是计算速度特别快，但多重散射理论也有一定的局限性，只能对散射体是球形和圆柱体的声子晶体进行计算.

本文的研究对象是由铁圆柱垂直没入水中形成的二维铁-水声子晶体，材料的主要参数为：铁柱的参数：密度7.67×103kg/m3，纵波速度6.01 km/s，横波速度3.23 km/s；基质水的参数：密度1.0×103kg/m3，纵波速度1.49 km/s，横波速度0 km/s.

多重散射理论是将弹性波(或声波)的波函数以球函数(三维)或柱函数(二维)为基函数进行展开，得到久期方程，利用自洽方法求解该本征方程，得到声子的本征频率.

本文所研究的声子晶体的久期方程为：

(1)

(2)

对于长宽比不同的七种矩形晶格，晶格基矢可分别表示为：

图1(a)展示了二维铁-水声子晶体在X-Y平面的横截面图，铁圆柱呈矩形晶格排列，晶格长宽分别为ax和ay.图1(b)是它相应的第一布里渊区示意图.

图1 (a) 二维声子晶体在xy平面的横截面图，圆柱形散射体呈矩形晶格排列(b)相应的第一布里渊区

在本文的计算中，取nmax=6，如前所述，久期方程(1)式就变成含有13×13个矩阵元的本征值方程.对于第一布里渊区的任一波矢k，通过计算能得到许多本征解，如果一个本征解用字母“n”标示，那么其本征频率就能相应写成ωkn.当波矢k沿着图1(b)所示的简约布里渊区边界Γ→Χ→Μ→Γ变化时，就能得到一系列由ωkn组成的曲线，这些曲线也就描述了该声子晶体的能带结构.

3 结果与讨论

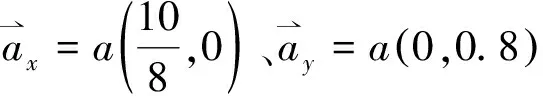
图2 正方晶格情况下填充率分别为0.5(a)和0.3(b)时的能带结构图

图3晶格基矢为的矩形晶格情况下填充率分别为0.5(a)和0.3(b)时的能带结构图

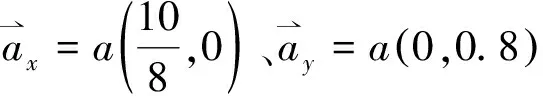
为了比较在不同矩形晶格和不同填充率情况下得到的带隙宽度，计算出了八种晶格在各自允许填充率范围内的相对禁带宽度，并以填充率为横轴、相对禁带宽度为纵轴作图，结果如图4所示.

图4 在不同矩形晶格和不同填充率情况下的相对禁带宽度

观察图4，发现对于二维铁-水声子晶体(高密度散射体放入低密度基质中)，在同一填充率下矩形晶格总是比正方晶格更容易得到较宽的带隙.并且，在同一填充率下如果矩形晶格长宽比越大，禁带宽度也越大.但对于矩形晶格长宽比越大的声子晶体，由于其可允许的最大填充率会越小，所以禁带宽度的变化范围也会越小.另外，在各晶格排列情况下最大的禁带宽度都是在最大填充率时取得.如果想增大声子晶体的禁带宽度，除了增大散射体的填充率使散射体尽可能相互靠拢外，另外一种可行的办法就是降低晶格的对称性.

4 结 论

运用多重散射理论，分析了晶格和填充率对带隙的影响.得到以下结论：对于二维铁-水声子晶体(高密度散射体放入低密度基质中)，无论是正方晶格还是矩形晶格，带隙总是出现在第一条能带和第二条能带之间，并且带隙宽度随填充率的增大而增大；在同一填充率下，矩形晶格长宽比越大，禁带宽度也越大.

参 考 文 献:

[1] SIGALAS M,ECONOMOU E N.Band structure of elastic waves in two dimensional systems[J].Solid State Commun,1992,86(3):141-143.

[2] KUSHWAHA M S,HALEVI P,DOBRZYNSKI L,et al.Acoustic band structure of periodic elastic composites[J].Phys Rev Lett,1993,71(13):2022-2025.

[3] KUSHWAHA M S,HALEVI P,MARTNEZ G, et al.Theory of acoustic band structure of periodic elastic composites[J].Phys Rev B,1994,49(4):2313-2322.

[4] VASSEUR J O,DJAFARI-ROUHANI B,DOBRZYNSKI L,et al.Acoustic band gaps in fibre composite materials of boron nitride structure[J].J Phys:Condens Matter，1997,9(35):7327-7342.

[6] ZHANG X,LIU Y Y,WU F G,et al.Large two-dimensional band gaps in three-component phononic crystals[J].Phys Lett A,2003,317(1-2):144-149.

[7] YANG S X,PAGE J H,LIU Z Y,et al.Focusing of sound in a 3D phononic crystal[J].Phys Rev Lett,2004,93(2):024301.

[8] PENNEC Y,DJAFARI-ROUHANI B,LARABI H,et al.Low-frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin homogeneous plate[J].Phys Rev B,2008,78(10):104105.

[9] WEN J H,YU D L,LIU J W,et al.Theoretical and experimental investigations of flexural wave propagation in periodic grid structures designed with the idea of phononic crystals[J].Chin Phys B,2009,18(6):2404-2411.

[10]DIEZ A,KAKARANTZAS G,BIRKS T A,et al.Acoustic stop-band in periodically microtapered optical fibers[J].Appl Phys Lett,2000,76(23):3481-3483.

[11]GOFFAUX C,MASERI F,VASSEUR J O,et al.Measurements and calculations of the sound attenuation by a phononic band gap structure suitable for an insulating partition application[J].Appl Phys Lett,2003,83(2):281-283.

[12]KHELIF A,CHOUJAA A,DJAFARI-ROUHANI B,et al.Trapping and guiding of acoustic waves by defect modes in a full-band-gap ultrasonic crystal[J].Phys Rev B,2003,68(21):214301.

[13]KHELIF A,CHOUJAA A,BENCHABANE S,et al.Guiding and bending of acoustic waves in highly confined phononic crystal waveguides[J].Appl Phys Lett,2004,84(22):4400-4402.

[14]LI X,LIU Z Y.Coupling of cavity modes and guiding modes in two-dimensional phononic crystals[J].Solid State Commun,2005,133(6):397-402.