八粒子量子态对彩色图像的存储方案＊

苏丹， 和伟， 吴经纬， 莫晶

（云南师范大学 物理与电子信息学院，云南 昆明650500）

人们获取的信息70%来自视觉系统，图像是信息的重要载体.图像数字化后数据量非常大，需要占据大量存储空间，而且图像的分辨率越高，组成一幅图的像素就越多，则图像文件就越大；同时，像素深度越深，表达单个像素的颜色和亮度的位数越多［1］，图像文件也就越大.量子衍生图像处理方法是量子衍生方法在图像处理领域的拓展，它为该领域的理论研究和技术实现提供了一种新的观念和思路.尽管在经典图像存储中提出关联记忆的方法［2］，然而在n比特关联记忆中存储图案数是o（n）时，这是一种无效的方案.在本文中，我们提出了一种基于量子态的彩色图像存储方法，借助于量子态的巨大存储能力，以及通过采用量子并行计算特性的Grover量子搜索算法［3］能起到平方根加速的理想效果.并且我们在图像存储和图像重构的过程中，对量子比特阵列进行搜索找到相应的彩色图像，这证明了所采用的方法有很好的效果.

1 量子比特描述

比特是经典信息与通信中最基本的概念，量子信息理论以及量子通信也建立在一个相似的概念基础之上，称之为量子比特［4］，与经典比特一样，量子比特也描述一种状态.经典比特常用0和1表示，量子比特也经常写成｜0〉和｜1〉形式，称为计算基矢，其中“｜〉”为dirac标记，一般用｜0〉表示0，用｜1〉表示1.与经典比特不同，量子比特不仅有｜0〉和｜1〉两种状态，这两种状态的任意线性组合又能表示其他的状态，任一状态表示为｜ψ〉＝α｜0〉＋β｜1〉，其中α、β是复系数，满足和｜1〉常称为正交基矢.当α＝0或β＝0时，量子比特退化为｜0〉和｜1〉，和经典比特具有一样的特性，此时量子比特退化为经典比特.以下是经典比特与量子比特的比较表：

表1 量子比特与经典比特的比较Table 1 Comparison of quantum bit and classical bit

2 像素量子比特表述

在图像从灰度空间到量子空间的映射过程中，首先要将图像灰度函数进行归一化变换处理，定义如下归一化变换函数为

其中f（x，y）∈［0，1］表示像素 （x，y）的归一化灰度值，xi，yj分别表示待处理图像g（x，y）的最大、最小灰度值，T和α是引入的两个参数，T称为灰度阀值，且T∈ （xi，yj），α∈ （0，1），I（x，y）为待处理的图像.从量子衍生的观点出发，定义如下像素量子比特表达形式为

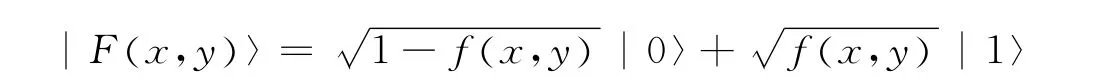
3 量子图像存储过程

对于一幅（三通道）彩色图像I和每个图像的像素（x，y）有如下关系式：

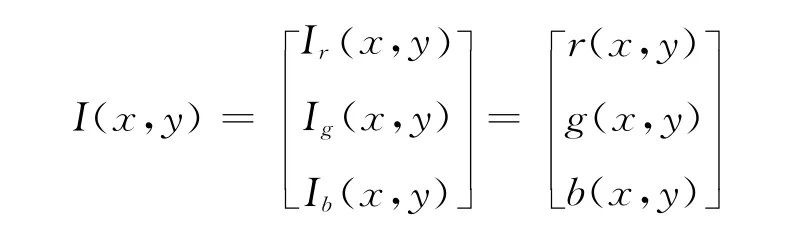
其中r、g、b为三个矢量分量，代表了自然界中的红绿蓝（r，g，b）三原色，而每种原色又被人为地分为了256（0～255）个灰度等级.首先对即将输入的彩色图像I进行彩虹变换［5］，即

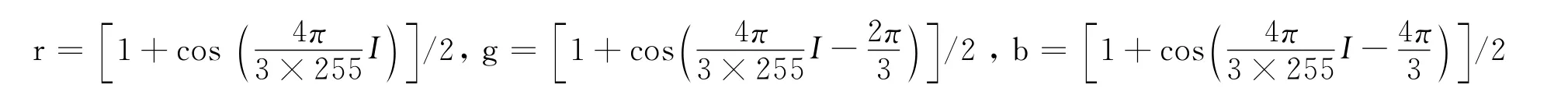
特别要指出，这三个周期函数按三者之一总会在所选择的彩色间隔中处于峰的位置来使用，如图1所示.

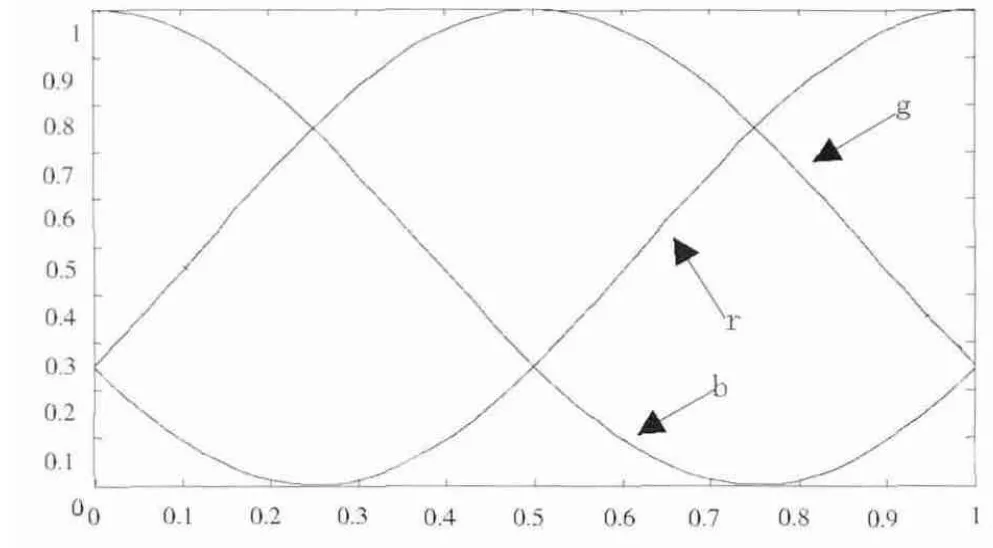
图1 彩色色标与用于彩虹变换的三个周期函数Fig.1 Colorful color codes and three periodic functions used for rainbow transformation

在量子系统中存储彩色图像时，考虑将一个n位量子比特阵列作为存储器，阵列中的每个量子位都包含两个与之相关的参量x和y，这两个参量一起表示二维图像的点，这样的一个量子比特阵列被用来存储视觉图像信息.在向该阵列输入信息前，假设每个量子比特的初始状态为｜0〉，那么寄存器的状态可用下列公式表达

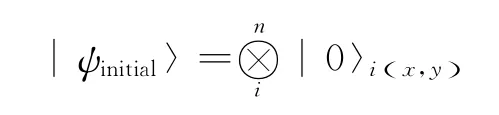
我们采用八个粒子所具有的28＝256个量子态来对每一种颜色的灰度等级进行编序描述，这样就可以用八个量子位按照二进制编码的规则来表示｜i〉.对灰度等级进行如下表示：

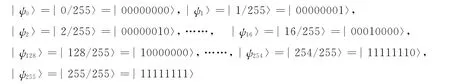
另外采用2粒子量子态对三基色进行区分，则对三原色中每一种颜色的存储只需确定其灰度等级，比如存储红色，灰度值为100时，寄存器标志位为｜01〉，寄存器中对应的位置为｜01100100〉；如果存储绿色，灰度值为128时，寄存器标志位为｜10〉，寄存器中对应的位置为｜10000000〉；如果存储蓝色，灰度值为64时，寄存器标志位为｜11〉，寄存器中对应的位置为｜01000000〉.

这样我们就可以用三个并列的量子比特阵列对该彩色图像的像素点进行存储，其中这三个量子比特阵列分别存储红、绿、蓝三种颜色的等级值.彩色图像上的每个像素点都可以用一个函数来表示，即

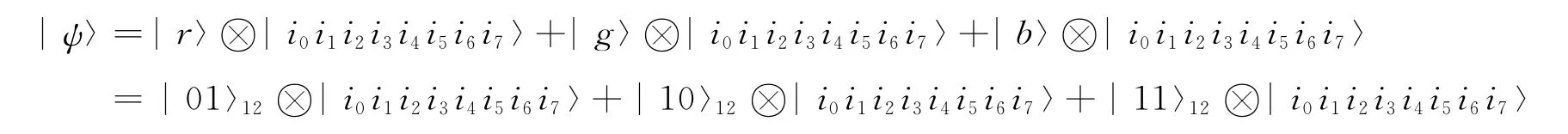
其中i∈ ｛0 ，1 ｝ .这样彩色图像的每个像素点可以被三个相同的八量子比特阵列分别赋值，彩色图像也就被存储了.

彩色图像被存储后，用检索信息来重构提取图像，图像信息的获取是通过对量子阵列的测量来实现.以存储红色灰度等级的N比特的量子寄存器和附加的一个1比特的寄存器来说明，过程如下：

（1）首先使用Walsh－Hadamard变换来初始化量子寄存器.此时量子寄存器的量子态为

（2）重复下列步骤m次，m为搜索次数.

①对于某个量子基态｜〉，如果满足C（｜〉）＝1，使用旋转操作R，将｜〉的概率幅旋转π，否则保持不变.R的定义为

②对量子基态概率幅向量应用矩阵D定义的幺正变换，放大所需量子基态的概率幅.矩阵的定义为

可以看到R算子的作用是对目标量子态进行旋转操作，D算子的作用是对目标量子态进行放大操作.

使用R、D算子对256个量子基态的量子寄存器进行操作（即量子搜索），然后进行测量.在测量成功概率第一次出现峰值的时候，进行测量，便能以较大概率获得目标量子态，这一次数即为使用Grover算法进行搜索的理想搜索次数，约为次，其中N为量子寄存器中量子基态的数量.另外通过经典算法与Grover算法性能的比较，可以看出如果一个处于乱序状态的数据库［6］包含N个元素，采用经典算法需要进行N次搜索，而利用Grover算法搜索只要进行次搜索，便能以较大概率获得目标［7］，如下表所示（以数据库中包含256个元素为例）：

表2 经典算法性能与Grover算法性能的比较Table 2 Comparison of performance between classic algorithm and Grover algorithm

实际上，量子比特阵列中的任何一个存储态都包含一个｜ψinitial〉和其他存储态的相干叠加态，因此不同图像的存储态是非正交的，因而不能明确地区分，也就是说利用投影算子仅能给出各个像素点的位置的概率结果，不能由此完全正确地重构图像.相对应地，可以使用探测各个像素点量子比特纠缠的量子测量来确定各个像素点的位置.现已推导出N粒子纠缠态贝尔型不等式，这表明对N个像素点的这种存储方法是可行的.因此从理论上，量子阵列能够存储任意复杂的多个像素点的图片.可以为了找到这个存储的彩色图像，在量子阵列中选取一系列N个量子比特构成的一组进行测量，判断他们是否违背Seevinck－Svetlichny不等式［8－9］，如果违背该不等式表明当前的N个点量子纠缠态为完全纠缠，属于同一幅图片，如果不违背则表明当前的N个点则不是同一幅图像，由这个信息就可以直接得出存储图像重构后的结构轮廓.对于一幅彩色图像而言，则需要次［10］不同的测量来检测一幅彩图纠缠在量子比特阵列中.

4 结束语

本文利用量子态作为载体在量子比特阵列中存储彩色图像，通过RGB彩色空间到量子比特空间的映射，很好地解决了在量子纠缠系统中存储彩色图像的问题.另外，彩色图像在量子阵列中的存储还有很多需要改进的地方，可以做进一步的研究.

［1］朱秀昌，刘峰，胡栋.数字图像处理与图像通信［M］.北京：北京邮电大学出版社，2006.

［2］KOHONEN TEUVO.Self－organization and associative memory［M］.3rd ed.London：Springer－Verlag New York，Inc.Berlin and Heidelberg GmbH ＆ Co.K，1989.

［3］GROVER L K.Quantum mechanics helps in searching for a needle in a haystack［J］.Physical Review Letters，1997，79（2）：325－328.

［4］NIELSEN MICHAEL A，CHUANG ISAAC L.Quantum computation and quantum information［M］.London：Cambridge University press，2000.

［5］KOSCHAN ANDREAS，ABIDI MONGI.Digital color image processing［M］.Indiana：Wiley Publishing，Inc.，2009.

［6］GROVER L K.A fast quantum－mechanical algorithm for database search［C］.The 28th Annual ACM Symposium on Theory of Computing，New York：ACM Press，1996，212－219.

［7］陈洪光，李飚，沈振康.逼近全概率 Grover算法的搜索次数计算［J］.计算机工程与应用，2004，40（3）：67－59.

［8］SEEVINCK M，SVETLICHNY G.Bell－type inequalities for partial separability inN－particle systems and quantum mechanical violations［J］.Physical Review Letters，2002，89（6）：060401.

［9］COLLINS D，GISIN N，POPESCU S，et al.Bell－type inequalities to detect true n－body nonseparability［J］.Physical Review Letters，2002，88（17）：170405.

［10］RIEFFEL E，POLAK W.An Introduction to quantum computing for non－physicists［J］.ACM Computing Surveys，2000，32（3）：300－335.