间接加热式列管回转干燥机传热系数的测试方法

吴静，李选友，陈宝明，王瑞雪，高玲

（1山东大学能源与动力工程学院，山东 济南 250014；2山东天力干燥股份有限公司，山东 济南 250101；3山东建筑大学热能工程学院，山东 济南 250101）

研究开发

间接加热式列管回转干燥机传热系数的测试方法

吴静1，2，李选友2，陈宝明3，王瑞雪2，高玲2

（1山东大学能源与动力工程学院，山东 济南 250014；2山东天力干燥股份有限公司，山东 济南 250101；3山东建筑大学热能工程学院，山东 济南 250101）

在对列管回转干燥机内传热过程进行深入分析的基础上，设计了简便、可靠的实验系统，并运用非稳态传热理论导出列管壁面与物料颗粒间的传热系数与被测量参数的关系式，从而建立了一套用于间接加热式列管回转干燥机的加热管壁面与物料颗粒间传热系数的测试方法。实验装置的传热系数测量结果显示，列管壁面与颗粒间的瞬时传热系数随筒体转动呈现周期性的变化规律，随着列管位置的升高，传热系数呈逐渐降低的趋势。通过对测试结果的误差分析表明，对传热系数测量精度影响最大的因素是紫铜管表面积，其余依次为壁面升温速率、加热电流、列管壁面温度和物料温度的测量。对常见的6种运行工况的传热系数测试结果进行了可靠性分析，结果表明，所产生的最大相对误差小于3.5%，壁面升温速率的测量误差是总误差的主要构成部分。

干燥；传热；测量；间接加热；列管回转干燥机

间接加热式列管回转干燥机（以下简称列管回转干燥机）是在传统的直接加热式回转干燥机的基础上加装加热列管形成的。加热管随筒体一起转动，蒸汽或热烟气或导热油等作为热源，通过加热管对筒体壳程空间内的物料进行加热，使其脱除水分达到干燥的目的。与传统的直接加热式回转干燥相比，列管回转干燥方式具有产品质量好、热效率高、环境污染小、安全性高等优点[1-3]，在诸如高分子聚氯乙烯（HPDE）、精对苯二甲酸（PTA）等化工产品干燥，褐煤、脱硫石膏等工业生产及玉米干燥等农产品加工中具有极大的应用空间，并且越来越受到相关行业的青睐[4-7]。

尽管国内外学者对传统的直接加热式回转干燥机（也称回转窑或转筒）内物料颗粒的运动规律和传热特性进行了一些理论分析[8-10]和实验研究[11-14]，但回转窑内加装加热列管后，物料颗粒的运动变得十分复杂，列管回转干燥机内的传热机理亦与传统直接加热式回转窑有着显著的差异。由于对列管回转干燥机内加热管壁面与颗粒间的传热机理缺乏足够的了解，迄今为止，尚无能够确切描述加热管壁与物料间传热过程的数学模型，工程设计中传热系数的确定仍依赖于实测或经验[15-18]。研究表明，加热管壁面与颗粒间的传热是列管回转干燥机内传热过程的重要组成部分，其热阻是影响总热阻的主要因素[18]。因此，准确测量加热管壁与物料颗粒间的传热系数对深入研究列管回转干燥机内的传热机理以及合理地进行工程设计具有十分重要的意义。干燥机的设计及其传热机理的研究提供实验支持。

1 实验装置及原理

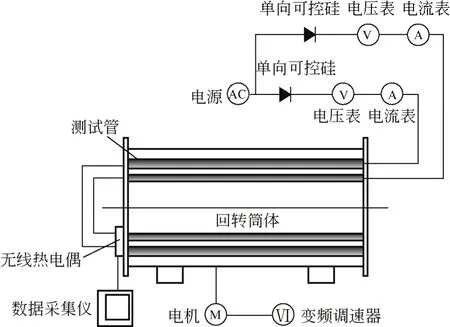
图1 实验系统图

Turton[19]、叶世超[20]、符鑫尧[21]等对流化床中浸没列管与两相流间传热系数的测试技术进行了研究，并建立了具有借鉴意义的测试方法。但就传热特性而言，列管回转干燥机却与流化床存在着明显的差异。在流化床中，列管始终浸没在沸腾的床层中，列管与床层颗粒间的传热可视为稳态过程。而在列管回转干燥机中，因筒体和列管的转动，列管与物料颗粒或气相之间进行周期性交替浸没，其传热也必然呈现出明显的周期性非稳态特征。本文旨在对列管回转干燥机内加热列管与颗粒之间的传热过程进行深入分析，并充分考虑非稳态传热特点的基础上，建立一套精准、可靠的列管壁面传热系数的测量方法及数据处理方法，以期为列管回转

图2 实验装置及筒体端面实物图

为测量列管回转干燥机内列管与物料颗粒间的传热系数，本文建立了一套独特的测试装置和系统，如图1、图2所示。该系统由回转筒体、列管、测试管、电动机、变频器、稳压电源、单向可控硅、电压表、电流表、可编程热电偶输入节点（ NI WSN-3212）、NI LabVIEW PXI以及显示器等组成。筒体及列管规格以及列管排布参照某实用装置在径向按一定比例缩小。筒体尺寸为φ380mm×580mm。筒体内以同心圆方式排列2圈列管，每圈列管沿圆周均布16根。靠近筒壁的外圈列管直径为32mm，内圈列管直径为25mm。为便于观测，筒体采用有机玻璃制作而成。其中，沿同一半径方向设置2根相应直径的测试管，如图2(b)所示，用于测量内圈和外圈列管的传热系数。其余列管均为相应直径的不锈钢管，不进行加热，仅用于构成筒体内的列管排布。回转筒体的传动系统由电动机、链轮、链条和托轮组成。电动机带动托轮实现筒体转动，通过调节变频器改变筒体转速。

用于测量传热系数的测试管由紫铜管、不锈钢管、绝缘骨架、热电偶、电热管等组成，如图3(a)所示。测试管总长度580mm，其中有效测试段为紫铜管，长200mm，壁厚1.5mm。测试段内安装有电热管，为测试过程提供稳定的热流。测试段两端与不锈钢管之间分别通过绝缘骨架进行连接，以防止电热管提供的热量传递至不锈钢管。在每根紫铜管的中间截面的外表面上均匀敷设4根直径0.1mm的热电偶，其并联输出的温度作为紫铜管壁面的平均温度。在每个紫铜管壁温测点的附近，分别通过设在管壁上的支撑结构对应固定一根直径0.1mm的热电偶，且使热电偶的探头离开壁面1mm距离，用以测量壁面温度测试点附近的颗粒相温度，将其并联输出的温度作为紫铜管近壁面的平均温度。壁面及近壁处的温度测试点设置如图3(b)所示。所有温度信号由热电偶发射器无线发送，由LabVIEW接收，并根据需要设置合适的数据记录间隔，实现温度的在线记录。电热管通过电滑环与可控硅连接，可控硅与稳压电源相连，输入功率由可控硅进行调节。如图1所示，为实现对内外圈测试管输入热量的独立调节和计量，对两根测试管分别设置了通电线路，并在各自的线路上分别设有可控硅、电流表和电压表，通过测量通入每根电热管的电流和电压值可计算每根电热管的发热量。因近壁面处的颗粒相温度测点离开管壁仅1mm的距离，远远小于相邻列管之间的间距，且每根测试管的电热管提供的热量较小，故其余列管的存在对测试管的热量及近壁面处颗粒相温度测量的影响可以忽略。测试管的实物如图4所示。

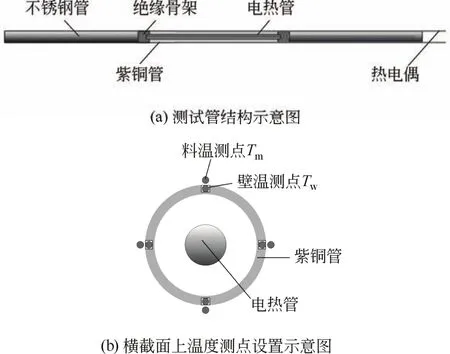
图3 测试管结构及温度测点设置示意图

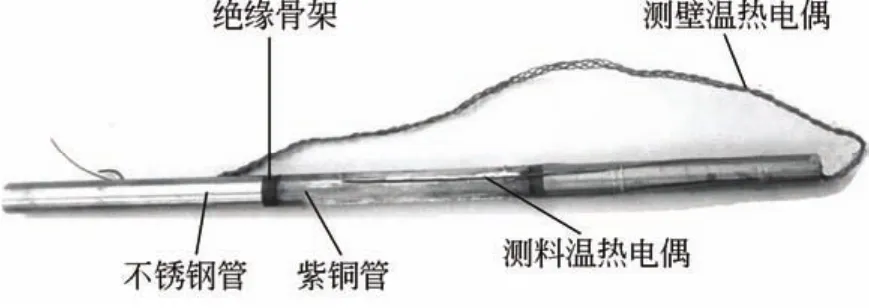
图4 测试管实物图

2 传热过程特点简析

观察发现[22]，在稳定的操作条件下，物料颗粒在干燥机筒体横截面上形成一个稳定的月牙状区域，近似悬浮于列管之间，颗粒相与气相存在一个明显的分界面，如图2(b)所示。列管在随干燥机筒体转动的过程中，以筒体转动频率为周期，在颗粒相与气相间交替浸没。由于测试管本身的蓄热作用及颗粒相与气相的物性差异，当测试管处于颗粒相时，管壁温度逐渐降低，处于放热状态；而当测试管处于气相时，管壁温度逐渐升高，测试管处于蓄热状态，如图5(a)所示。图5(b)为以直径2mm的陶瓷球为实验物料，在填充率30%、筒体转速5r/min的实验工况下测得的筒体旋转两周内的φ32mm测试管壁温随筒体转动的变化曲线。测试管的位置设定为：正下方位置定义为0°，沿筒体旋转方向依次定义0°～360°；测试管位于0°位置时的时刻定义为τ=0s。由图5(b)看出，列管在回转干燥机内的传热呈现出了明显的周期性非稳态特点。列管在完全浸没于颗粒相（AB及A'B'段）区间内，壁面温度逐渐减小；在完全浸没于气体相（BC及B'C'段）区间内，壁面温度逐渐升高。而在列管开始接触颗粒相至完全浸没于颗粒相的过渡区（CA'段）内，由于颗粒和气流运动的共同影响，温度变化规律较复杂。

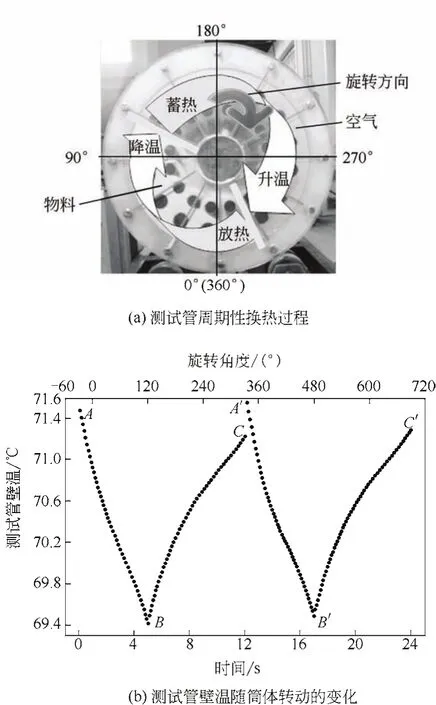
图5 测试管的周期性非稳态换热特点

3 测试方法的建立

为保证测量的稳定性和可重复性，本文选用具有良好分散性和流动性的陶瓷球作为实验物料。按照所设定的填充率及筒体转速等测试条件启动并调整实验系统后，给电热管通入一定的电流。在输入功率一定的情况下，经过一段时间的运行后，测试管壁温的变化曲线基本上保持稳定，此时开始记录各参数的测量值。测量中，在干燥机前端一定距离处安放一架摄像机（JVCGZ-GX8），拍摄记录各时刻测试管的位置，以便对LabVIEW的温度记录进行校验。

由于陶瓷球具有良好的导热性能，在受到列管充分搅拌的情况下，可以近似认为颗粒间的温度分布均匀。因此，在该测量系统中，可以认为测试管壁温测点附近的热电偶测得的温度为近壁处物料或气体的温度。

列管外壁与物料颗粒间的瞬时传热系数可表示为式（1）、式（2）[23]。

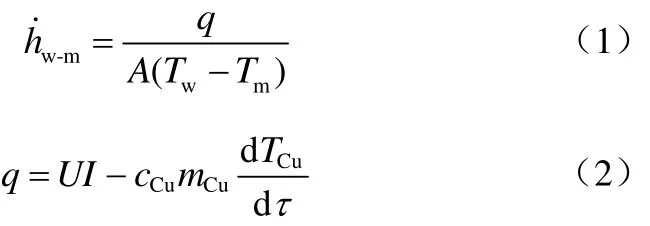
由于紫铜的导热系数非常大，而电热管的输入功率仅为60W左右，故有式（3）。

由式（1）～式（3），得式（4）。

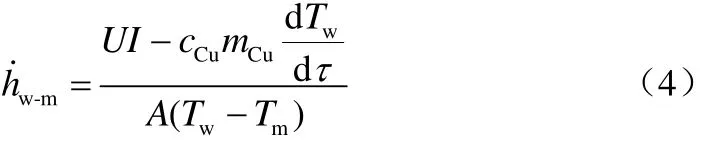
对于工程设计而言，最常使用的是列管与物料颗粒之间的平均传热系数，可通过式（5）求取。

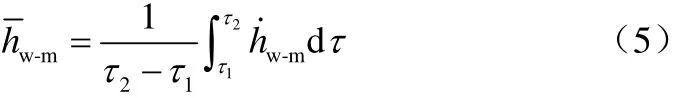
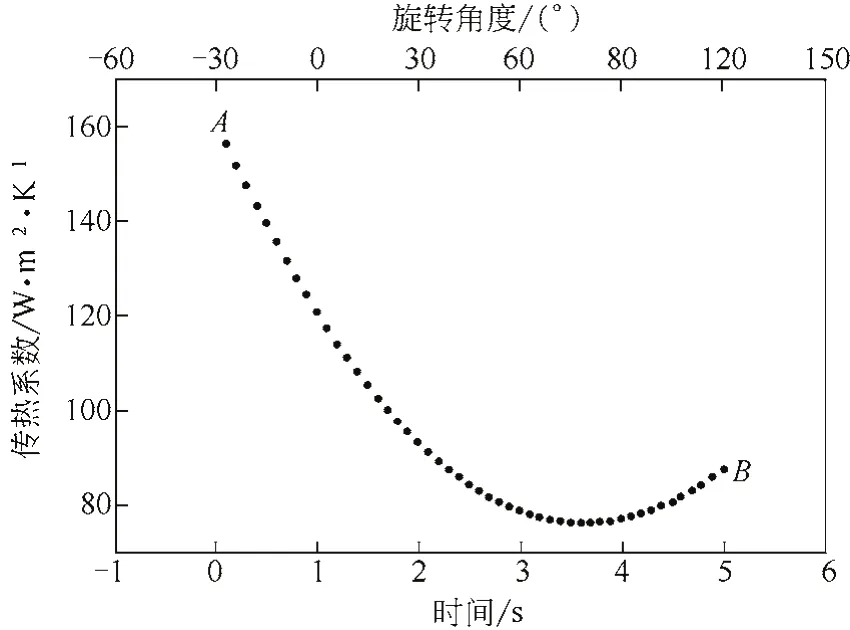
图6 完全浸没于颗粒相中的测试管壁面瞬时传热系数的变化

式中，τ1和τ2分别为测试管完全浸没于颗粒相的起始时刻和结束时刻。

图6为采用上述测试方法对φ32mm测试管分析获取的列管与颗粒间传热系数的一个示例。实验以直径2mm的陶瓷球为实验物料，实验工况条件与图5相同。由图6可见，在完全浸没于颗粒相的区间内，随着列管位置的升高，列管与物料颗粒间的瞬时传热系数逐渐减小。根据本文作者所建立的传热模型分析[24]，其原因可能是在筒体转动和列管搅拌的共同作用下，高处的颗粒群比低处颗粒群的膨胀量大，从而导致列管壁面形成的气体边界层增大，进而使列管表面与颗粒间的传热系数减小。

4 可靠性分析

令k表示升温速率，则式（4）可表示为式（6）。

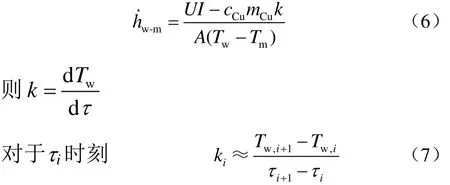
式中，ki为τi时刻的壁面升温速率，K/s；Tw,i+1和Tw,i分别为τi+1时刻和τi时刻的测试管壁面温度，K。

根据误差传递理论[25-27]，在某位置点的测试管壁面与颗粒间传热系数测试结果可能的最大绝对总误差为式（8）。

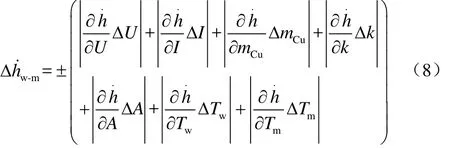
式中，ΔU、ΔI、ΔmCu、ΔA、ΔTw、Δk和ΔTm分别为各参数测量的最大绝对误差。式（7）中升温速率为温度差和和时间差的函数。测试中温度和时间均在较小范围内变化，两者的系统误差均可视为固定值，不计入ΔTw和Δτ中。而升温速率的误差Δk仅为测量的随机误差，本文取其均方差[26]，即式（9）。

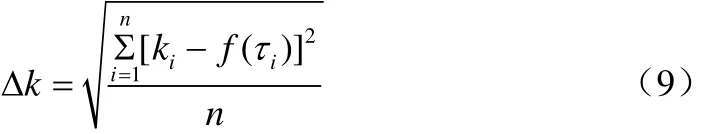
式中，f(τi)为τi时刻升温速率随时间变化的拟合值，K/s；n为记录数据点的数量。

由式（6）～式（8）可得在某位置点的测试管壁面与颗粒间传热系数测试结果的最大绝对总误差，如式（10）。

式（10）右端的各项分别表示了由电压、电流、紫铜管质量、管壁升温速率、加热面积、壁面温度、物料温度等各因素测量的绝对误差值而对应产生的传热系数测量绝对误差，分别表示为e(U)、e(I)、e(mCu)、e(k)、e(A)、e(Tw)、e(Tm)。用上述各项分别与测得的平均传热系数的比值表示由各因素测量误差而产生的传热系数相对误差，分别由δU、δI、δmCu、δk、δA、δTw、δTm表示，即有式（11）。

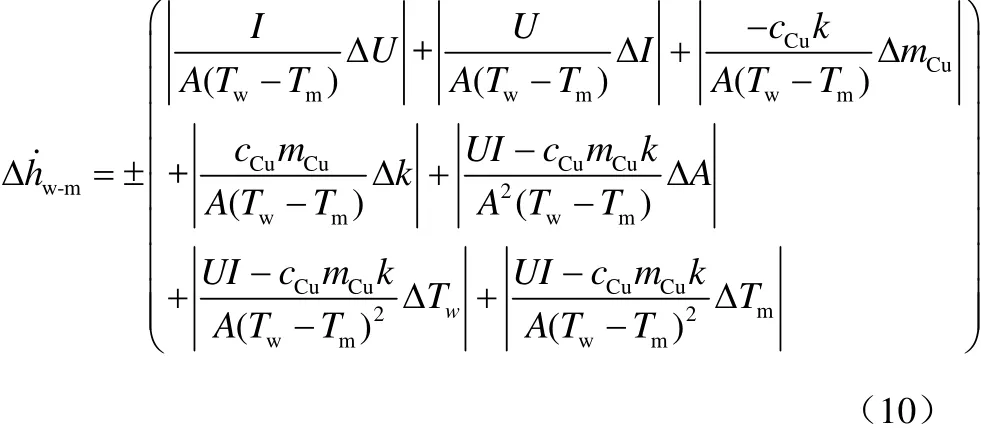
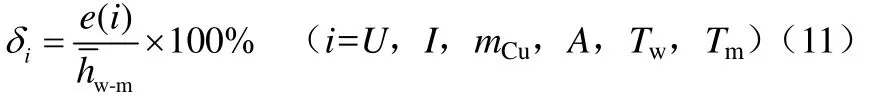
传热系数测量可能产生的最大总相对误差δ为式（11）计算的各项之和，表达为式（12）。

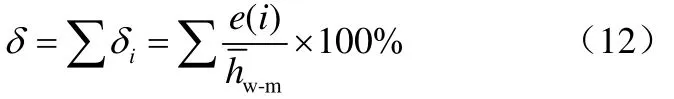
为保证各参数测量的精度，实验选取了较高准确度的电流、电压及温度测试仪器。电流和电压的测量选用美国Tektronic DMM4040型号的数字万用表，AC电压和AC电流的测试量程分别选取为0～100V和0～1A。以最大量程作为测试值时，按照其说明书规定的准确度计算方法，确定其测试准确度分别为0.1V和0.001A。测温热电偶选用K型Ⅰ级热电偶，为提高包括热电偶、无线发射器和LabVIEW在内的测温系统的整体准确度，采用二等标准水银温度计对测温系统在0～99℃范围内进行了多次标定，保证了测温系统的准确度达到0.1℃。本文测试方法中所用仪器及准确度列于表1中。

为分析测试方法的误差，结合设备实际运行时的操作参数范围，本文选取了如表2所示的6种实验工况进行了测试。

表1 各因素测量仪器及准确度

定义式（10）右端ΔU、ΔI、ΔmCu、ΔA、ΔTw、Δk和ΔTm前的各项系数为相应各因素测量误差的误差传递系数，该系数可反映总误差对相应因素测量误差的敏感度。根据实验中实际测试的参数值，按照式（10）计算出各因素测量的误差传递系数，结果列于表3。其中，计算所用温度为相应周期的平均值。可见，总误差对各实验因素测量误差的敏感度存在明显的差异。其中换热面积A的计量精度对总误差的影响最大，其次为壁面升温速率k的测量、电流I的测量，而壁面温度、物料温度、电压及紫铜管质量的测量对总误差的影响较小。所幸目前常见的用于尺寸计量以及可选的电流测量的仪表均具有较高的准确度，能够将其对总误差的影响控制在较小范围内。而本文根据上述误差分析，采用了经过标定的LabVIEW温度测试系统，也使壁面升温速率和温度及时间实现了高精度的测量，有效保证了传热系数测量的准确性。

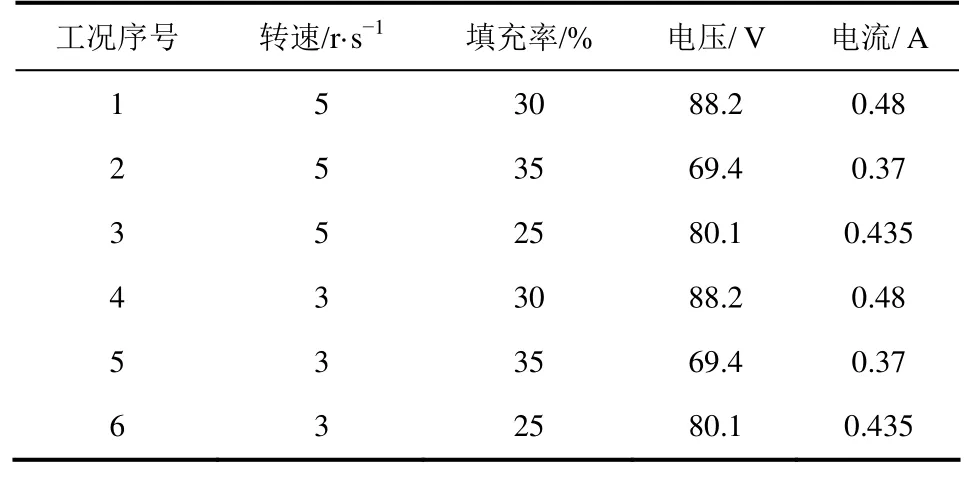
表2 实验工况条件表

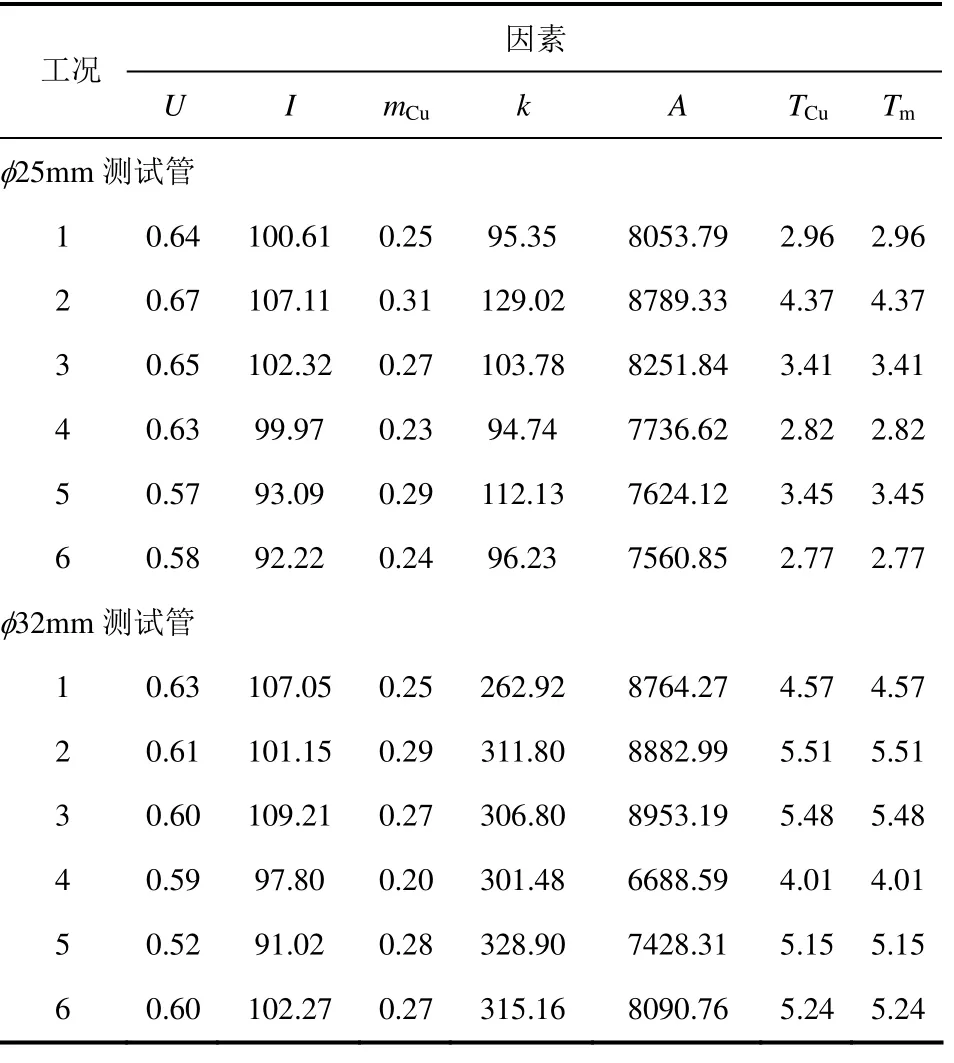
表3 传热系数总误差对各实验因素测量误差的敏感度

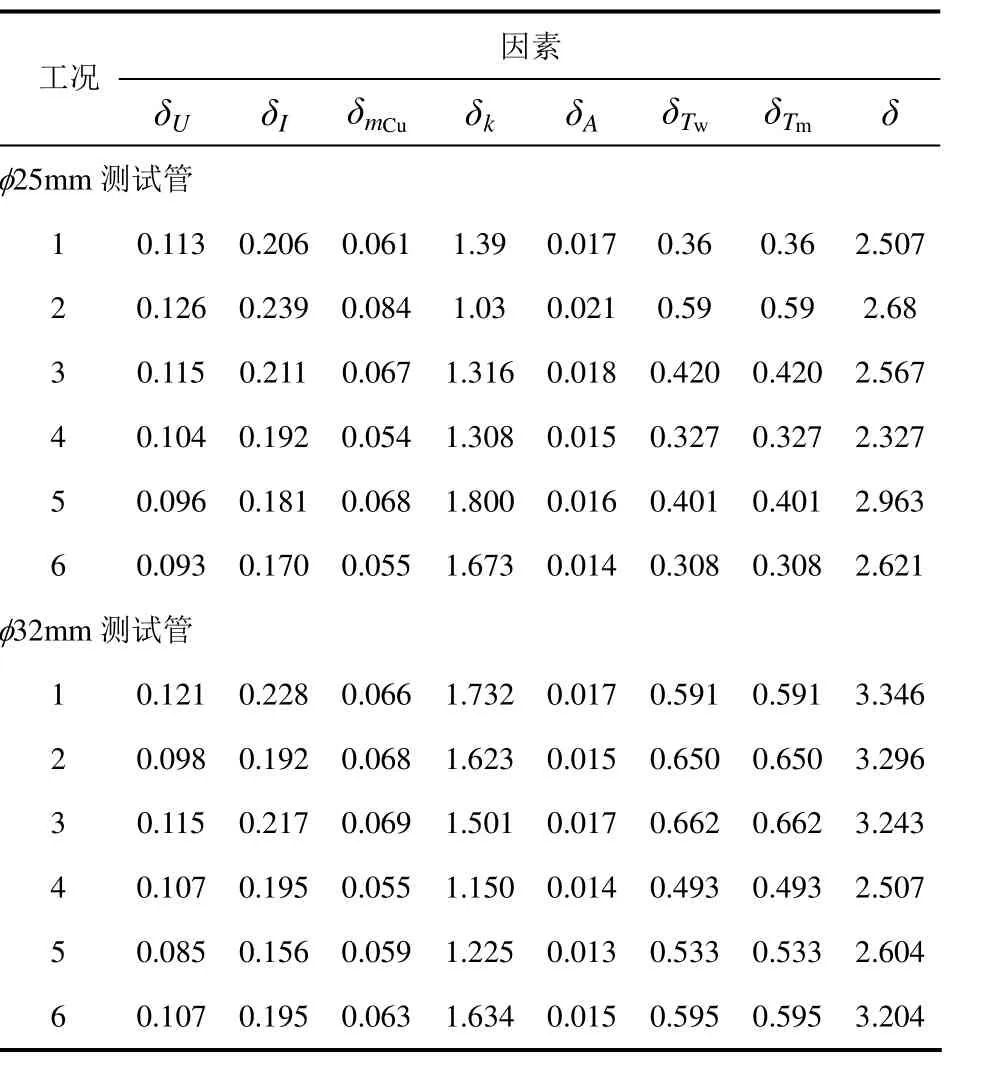
表4 各因素测量误差导致的各部分相对误差及传热系数的最大总相对误差 单位：%

针对表2所列各实验工况，由式（11）可计算获得各实验工况条件下由各因素测量的最大绝对误差而导致的传热系数相对误差；由式（12）可计算获得各实验工况条件下传热系数测量的最大总相对误差。将各因素测量误差导致的各部分相对误差及传热系数的最大总相对误差列于表4中。对表4的误差结果分析显示，在本文的6种测试工况条件下，所测得的φ25mm和φ32mm列管外壁与物料颗粒表面间传热系数可能产生的最大相对总误差分别为2.963%（工况5）和3.346%（工况1）。计算表明，对于本文所用测试系统，误差主要源于对升温速率k、壁面温度Tw和物料温度Tm的测量。其中，对于φ25mm测试管的工况5和φ32mm测试管的工况1，升温速率k的测量所产生的相对误差分别为1.8%和1.732%，壁面温度Tw和物料温度Tm测量所产生的相对误差分别为0.401%和0.591%。其余因素测量产生的相对误差均小于0.3%。对于误差传递系数最大的紫铜管表面积，因其测量的准确度为10-6m2，使其实际产生的相对误差值仅为0.016%和0.017%；同样，因电流测量的准确度为0.001A，使其实际产生的相对误差值仅为0.181%和0.228%。可见在本文的测量系统中，管壁升温速率的测量误差是测试系统总误差的主要构成部分。因此，减小紫铜管的质量以及提高温度、电流等仪表的精度等级并增加升温速率的测量次数是进一步提高测量精度的途径。

5 结 论

（1）本文在对列管回转干燥机内加热列管与颗粒之间的传热过程进行深入分析的基础上，充分考虑非稳态的传热特点，建立了一套精准、简便、可靠的列管壁面传热系数的测量及数据处理方法。

（2）分析了传热系数总误差对各实验因素测量误差的敏感度。换热面积的计量精度对总误差的影响最大，其次为壁面升温速率、加热电流的测量，而壁面温度、物料温度、电压及紫铜管质量的测量对总误差的影响较小。

（3）对本文采用的测试系统及选用的6种常见测试工况测试结果的可靠性分析表明，该方法具有较高的测试精度，可能产生的最大相对误差小于3.5%。而升温速率的测量误差是测试系统总误差的主要构成部分。减小紫铜管的质量以及提高温度、电流等仪表的精度等级并增加升温速率的测量次数是进一步提高测量精度的途径。

（4）列管在完全浸没于颗粒相的区间内，传热系数随着测试管位置的升高呈逐渐下降的趋势。

符 号 说 明

A——紫铜管的表面积，m2

cCu——紫铜管比热容，kJ/(kg·K)

——加热管壁与物料颗粒间的瞬时传热系数，W/(m2·K)

——加热管壁与物料颗粒间的平均传热系数，W/(m2·K)

I——输入电热管的电流，A

k——壁温升温速率，K/s

mCu——紫铜管的质量，kg

n——记录数据点的数量

q——测试管传递给物料颗粒的热流量，kW

Tm——近壁处物料的温度，K

Tw——紫铜管壁的温度，K

U——输入电热管的电压，V

ΔA——面积测量的最大绝对误差，m2

ΔI——电流测量的最大绝对误差，A

Δk——升温速率测量的最大绝对误差，K/s

ΔmCu——紫铜管质量测量的最大绝对误差，kg

ΔTm——物料温度测量的最大绝对误差，K

ΔTw——紫铜管壁面温度测量的最大绝对误差，K

ΔU——电压测量的最大绝对误差，V

τ——时间，s

e(i) ——由因素i测量的绝对误差值而对应产生的传热系数测量绝对误差

δi——由因素i的测量误差而产生的传热系数相对误差

δ——传热系数测量可能产生的最大总相对误差

下角标

Cu——紫铜管

m——物料

w—— 管壁

w-m——管壁与物料颗粒之间

[1] 金国淼. 化工设备设计全书干燥设备[M]. 北京：化学工业出版社，2002：298-301

[2] 汪政富，刘佳，方舒正，等. 苹果渣回转干燥器干燥数学模型及工艺优化[J]. 农机化研究，2009（1）：163-165.

[3] 吕新宇，王猛，杨欢，等. 间接换热式列管回转干燥机传热系数的研究[J]. 常州大学学报，2010，22（2）：38-41.

[4] 邢召良，王宏耀，陈洪军，等. 蒸汽回转石膏煅烧机的应用[J]. 新型建筑材料，2007（2）：15-18.

[5] 周立荣，钱国俊. 蒸汽管回转干燥机在燃褐煤电厂中的应用探讨[J]. 电力建设，2011，32（5）：94-99.

[6] 隋国亮，刘月红，杜翎. 美国大型玉米湿磨工厂的脱水和干燥设备[J]. 粮食与饲料工业，2011（6）：23-24.

[7] 周立荣. 蒸汽管回转干燥机在褐煤干燥上的应用[J]. 煤炭加工与综合利用，2010（6）：34-37.

[8] Patisson F，Lebas E，Hanrot F. Coal pyrolysis in a rotary kiln：Part I. Model of the pyrolysis of a single grain[J].Metallurgical and Materials Transactions. 2000，31B（2）：381-390.

[9] Descoins N，Dirion J L，Howes T. Solid transport in a pyrolysis pilot-scale rotary kiln：Preliminary results—stationary and dynamic results[J].Chemical Engineering and Processing，2005，44：315-321.

[10] 马爱纯，周孑民，孙志强，等. 氧化铝熟料窑内一维传热模型[J]. 冶金能源，2004，23（1）：23-26.

[11] Le Guen Laurédan，Huchet Florian，Dumoulin Jean，et al. Convective heat transfer analysis in aggregates rotary drum reactor[J].Applied Thermal Engineering，2013，54：131-139.

[12] Chaudhuri Bodhisattwa，Muzzio Fernando J，Omassone M Silvina. Experimentally validated computations of heat transfer in granular materials in rotary calciners[J].Powder Technology，2010，198：6-15.

[13] Fabian Herz A，Iliyan Mitov，Eckehard Specht，et al. Influence of operational parameters and material properties on the contact heat transfer in rotary kilns[J].International Journal of Heat and Mass Transfer，2012，55：17941-7948.

[14] 黄志刚. 转筒干燥器中颗粒物料流动和传热传质过程的研究[D].北京：中国农业大学，2004.

[15] 赵旭，应洪山，岳永飞. HDPE蒸汽管回转干燥机的工艺计算[J]. 化工机械，2000（1）：20-22.

[16] 吴静，王宏耀，李选友，等. 间接换热式列管回转干燥机换热系数的确定及研究[J]. 山东科学：自然科学版，2007，20（4）：65-71.

[17] 潘永康，王喜忠，刘相东. 现代干燥技术[M]. 第2版. 北京：化学工业出版社，2007.

[18] 岳永飞，孙中心，刘永忠. 蒸汽管回转干燥机传热系数研究[J]. 石油化工设备，2008，37（1）：8-11.

[19] Turton K. The measurement of instantaneous heat transfer coefficients around the circumference of a tube immersed in a high temperature fluidized bed[J].Int. J. Heat Mass Transfer，1992，35：3397-3406.

[20] 叶世超，陈晓东，李川娜，等. 振动流化床与浸没水平管间局部传热系数的测试方法[J]. 高校化学工程学报，2000，14（2）：188-193.

[21] 符鑫尧，蔡梅英，黄晓，等. 流化床埋管表面局部热流测试装置的研制[J]. 华中科技大学学报：自然科学版，1991，19（2）：101-106.

[22] Wu Jing，Li Xuanyou，Wang Hongyao，et al. Experimental study on heat transfer coefficient in a rotary tube dryer[J].Asia-Pacific Journalof Chemical Engineering，2011，6：312-315.

[23] 杨世铭，陶文铨. 传热学[M]. 第4版. 北京：高等教育出版社，2006.

[24] 吴静，李选友，陈宝明，等. 间接加热式列管回转干燥机传热系数模型构建[J]. 农业工程学报，2013，29（14）：53-59.

[25] 杨惠连. 误差理论与实验设计[M]. 北京：机械工业出版社，1988.

[26] 梁晋文，陈林才，何贡. 误差理论与数据处理[M]. 北京：中国计量出版社，1989.

[27] 钱政，王中宇，刘桂礼. 测试误差分析与数据处理[M]. 北京：北京航空航天大学出版社，2008.

Research on measuring heat transfer coefficient in an indirect heating tube rotary dryer

WU Jing1，2，LI Xuanyou2，CHEN Baoming3，WANG Ruixue2，GAO Ling2
（1School of Energy and Power Engineering，Shandong University，Jinan 250014，Shandong，China；2Shandong Tianli Drying Technology Co.，Ltd，Jinan 250101，Shandong，China；3Department of Thermal Engineering，Shandong Jianzhu University，Jinan 250101，Shandong，China）

This paper presented a simple and reliable device system for the measurement of heat transfer coefficient between the immersed tube’s surface and particles in an indirect heating tube rotary dryer，based on analysis of heat transfer process in a tube rotary dryer. A mathematical model to derive heat transfer coefficient from the measured parameters was developed based on the unsteady heat transfer performance. Periodical instantaneous heat transfer coefficient between tube’s surface and particles was observed as the tube rotating with the cylinder. Low heat transfer coefficient was observed at the high position when the tube was immersed in the particle phase. Analysis of error transfer showed that the accuracy of heat transfer coefficient was sensitive to the measurement accuracy of tube surface area，tube’s surface temperature increasing ratio，electric current，temperatures of tube surface and materials. Test results also demonstrated that under the common six operating conditions in this paper，the developed measuring approach yielded high accuracy of heat transfer coefficient with relative error less than 3.5%，and the total measurement error was mainly composed ofthe error of tube’s surface temperature increasing ratio.

drying；heat transfer；measurement；indirect heating；tube rotary dryer

TK 173

A

1000-6613（2014）09-2266-08

10.3969/j.issn.1000-6613.2014.09.006

2014-01-26；修改稿日期：2014-04-03。

国家自然科学基金项目（51076086）。

吴静（1975—），女，博士研究生，高级工程师，主要从事干燥技术及热能利用技术的研究。E-mail wujingsd@163.com。联系人：李选友，研究员，主要从事传热传质及工业节能技术的研究。E-mail lixuanyou_sd@163.com。