复杂形状波力直线发电装置的优化

林礼群，吴必军，王幸，吴春旭，王文胜

（1.中国科学院广州能源研究所，广东广州510640；2.中国科学院可再生能源与天然气水合物重点实验室，广东广州510640；3.中国科学院大学，北京100049）

复杂形状波力直线发电装置的优化

林礼群1，2，3，吴必军1，2，王幸1，2，吴春旭1，2，3，王文胜1，2

（1.中国科学院广州能源研究所，广东广州510640；2.中国科学院可再生能源与天然气水合物重点实验室，广东广州510640；3.中国科学院大学，北京100049）

针对漂浮式波浪能转换装置的能量转换特性问题，以漂浮双浮体直线发电波浪能装置为研究对象，基于线性波理论和粘性阻尼理论，建立了复杂形状波能装置的双自由度受迫振动方程，推导了最佳弹簧和最佳阻尼下波能装置的最佳吸收功率函数表达式和相对位移幅值表达式；基于边界元方法的HydroStar软件计算了复杂形状波能装置水动力学系数和波浪激励力。数值计算表明：在满足装置吸收最大功率的条件下，最佳弹簧系数在一定波况下出现了负值；在无弹簧的最佳阻尼条件下，装置的相对位移幅值小于波幅，波浪能功率和俘获宽度比在给定入射波周期范围内出现峰值。

波浪能；直线发电机；Hydrostar；最佳阻尼；最佳弹簧；俘获宽度比

关于波浪能发电技术的种类存在多种分类，根据首级吸收能量方式分类，主要有振荡水柱式、越浪式和振荡浮子式［1］。漂浮双浮子波浪能直线发电技术属于振荡浮子式，通过直线发电机直接把振荡浮子吸收的波浪能转换为电能，由于其转换环节少、结构简单而成为波浪能利用技术的一个研究热点［2-3］。

研究双浮子波浪能直线发电技术的功率转换特性是设计装置前提和一个重要的工作，其涉及到水动力学计算、能量转换理论和直线发电机设计等。郑永红，Berggren等［4-7］采用解析方法详细研究了由2个圆柱作垂荡运动的水动力学系数和波浪激励力；Eriksson［8］对一种直驱式波能装置在规则波和实海况下的运动状态和转换效率进行了理论研究；Valério、吴必军等［9-12］对双圆柱形浮体在假设水下浮体不动只考虑水面浮体垂荡运动的情况下单自由度有阻尼垂荡运动下装置效率转换特性问题进行了详细研究，以及对双圆柱浮体在双自由度有阻尼垂荡运动的情况下，装置吸收的功率特性进行了一些理论研究。

上述所列文献主要采用线性波理论和解析方法计算平面波作用下标准圆柱体的水动力学系数和波浪激励力，对于非标准圆柱形复杂波浪能装置的水动力学系数和波浪激励力的求解未见报道；在对波能装置的最佳吸收功率研究中，吴必军［12］推导出双自由度有阻尼垂荡运动的波能装置吸收功率表达式，并选取特定算例对装置的转换效率做了分析，但没给出波能装置在最佳弹簧和最佳阻尼下的最大吸收功率函数。

本文把弹性系数和阻尼系数分别作为独立变量对功率函数求极值，最后得到优化后的波能装置吸取波浪能的功率表达式。利用HydroStar软件和Mathematica软件对非标准圆柱体的复杂波浪能装置建模、计算水动力学系数和波浪激励力，求解最佳阻尼、最佳弹簧和最佳功率。分析在一定入射波条件下，波能装置的幅值响应特性和能量吸收特性，并结合实际波况条件和在直线电机冲程范围内所能提供的阻尼条件下，给出波能装置优化设计措施。

1 波能装置双自由度运动数学模型

所研究的漂浮直驱式波能装置如图1所示，水面浮体1为一圆柱锥形台状浮子，振荡浮子通过柔性绳与直线电机的动子部分连接，水下浮体2由圆柱形阻尼板和装有直线电机的中心管构成，直线发电机的线圈部分固定在中心管内，动子通过弹簧与阻尼板连接。在波浪作用下，水面浮体1与水下浮体2做相对运动使直线发电机的线圈做切割磁感线而发电。

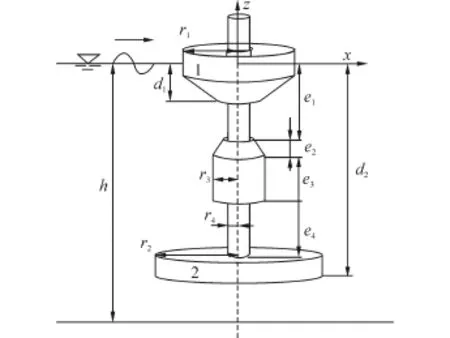
图1 波能装置几何特征Fig.1 Sketch of the wave energy device

设波能装置由电磁力提供一个粘性阻尼，阻尼系数为C，通过该阻尼波能装置吸收波浪能。装置的弹簧刚度为K。假设装置漂浮在不可压、流动无旋的波面上，在线性波作用下两浮体分别做微幅垂荡运动。

在以上假设条件下，波能装置中的振荡浮子1在垂直方向上受重力M1g，浮力Ff1，静水回复力Fs1，反电磁力Fgen（阻尼力），弹性力Fk，振荡浮子1自身运动产生的垂向波浪辐射力Frz11，浮体2运动作用在浮体1上的垂向波浪辐射力Frz12，浮体1所受的垂向波浪力为Fez1，波能装置中的水下浮体2在垂直方向上受重力M2g，浮力Ff2，静水回复力Fs2，阻尼力Fgen，弹性力Fk，浮体2自身运动产生的垂向波浪辐射力Frz22，浮体1运动作用在浮体2上的垂向波浪辐射力Frz21，浮体2所受的垂向波浪力为Fez2，则波能装置可简化为一个有阻尼的双自由度受迫振动系统，其数学模型简化为图2。

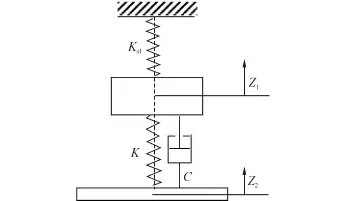
图2 双自由度振动模型Fig.2 Double degree freedom vibration model

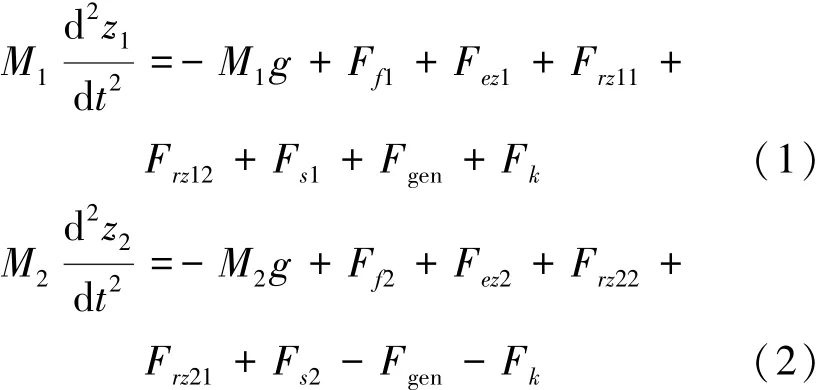
式中：浮体2的静水回复力可视为零，Fs2＝0；浮体n（n＝1，2）在静水平衡条件下分别有

垂荡运动的复数运动振幅为An，其位移方程表示为

浮体1的静水回复力可以表示为

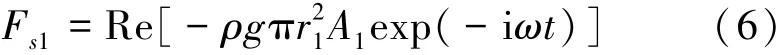
式中：ρ为海水密度，g为重力加速度，r1为浮体1的半径。电磁力和弹性力计算式：

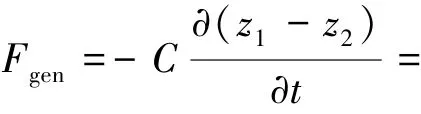
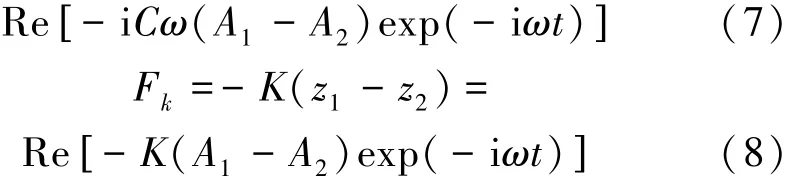
在线性波理论中，对浮体的垂荡运动，浮体n（n＝1，2）自身运动产生的垂向波浪辐射力Frznn，浮体m（m＝1，2）运动作用在浮体n上的垂向波浪辐射力Frznm，均可由下式统一表示：

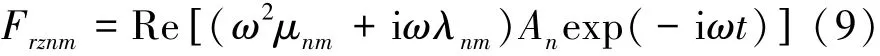
式中：μnm为附加质量，满足μnm＝μmn，（m≠n）；λnm为阻尼系数，满足λnm＝λnm，（m≠n）。波浪激励力Fezn为

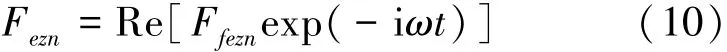
其中，Ffezn为空间项的激励力复数幅值。水动力学系数μnm、λnm、波浪激励力Ffezn和波浪辐射力Frznm将在第4节中计算出。

2 装置的幅值响应和吸收功率

把式（3）～（10）代入式（1）和式（2）去掉时间项最终化解为

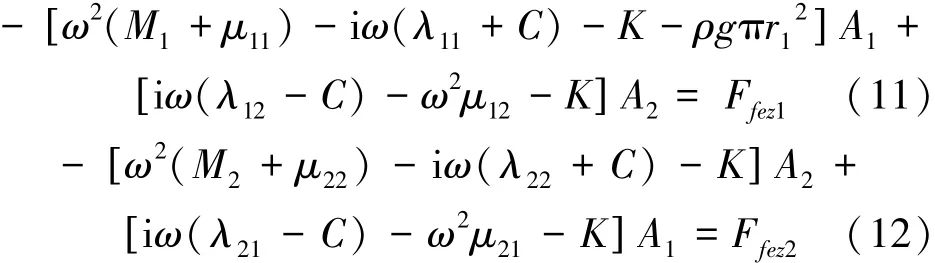
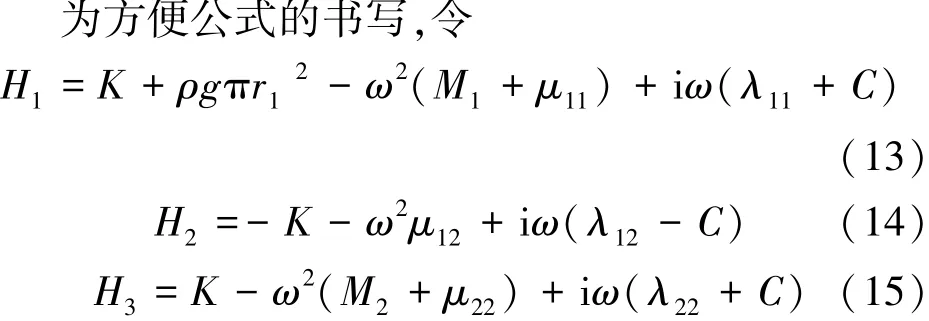
方程组进一步化简为

方程的解为

2个浮体的相对运动位移幅值为

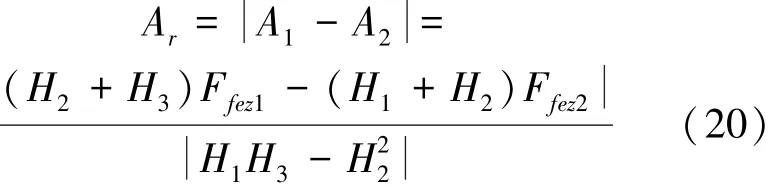
根据功的定义可知，阻尼力做的功就是波能装置吸收的能量，因此得到波能装置从波浪中吸收的功率为

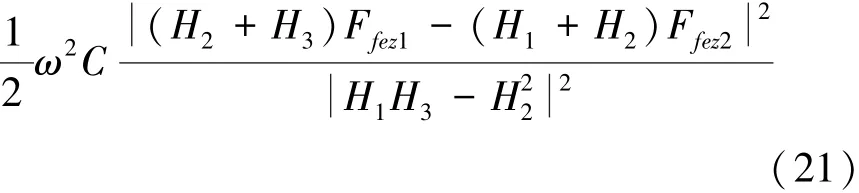
3 弹簧阻尼的优化方法

波能装置的吸收功率大小同海况（入射波周期、波高等）以及装置本身的结构设计（形状、阻尼力、弹力等）有关，本文在确定海况条件和装置形状尺寸条件下，以阻尼力和弹力作为研究变量，采用速度共振优化方法来求解式（21）中功率P的最大值，即把弹性系数和阻尼系数作为2个独立变量分别对功率函数求极值，最后得到优化后的波能装置吸取波浪能的功率表达式。为方便求极值计算，将式（21）中的分子项、分母项整理如下：

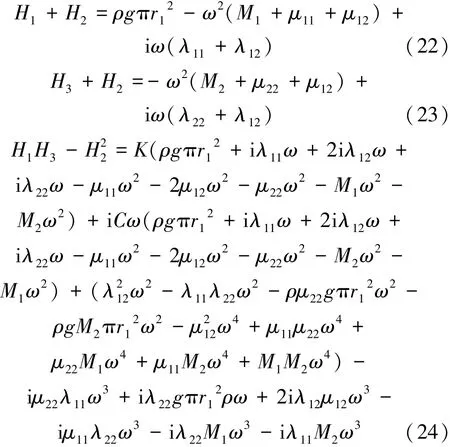
由式（22）、（23）知式（21）中分子项中不含变量K、C，可视为一常量，令

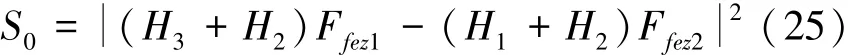
式（21）中的分母项可根据式（24）作变换：

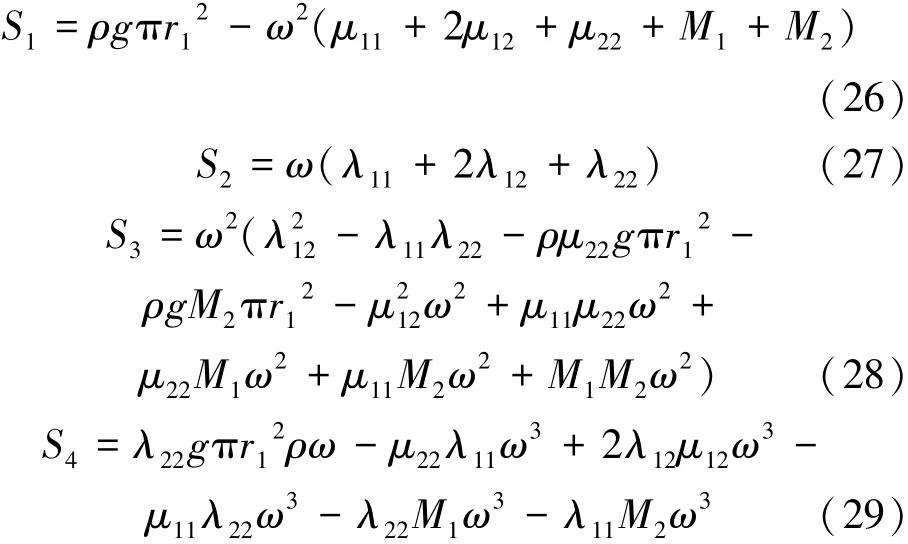
将式（26）～（29）代入式（24），式（21）中分母项可化简为

将式（25）、（30）代入式（21）得到波能装置吸收的功率为

因此，要使波能装置从波浪能吸收的功率P达到最大，必须满足

由式（33）、（34）可知，最佳弹簧Ko1与变量阻尼C无关，而最佳阻尼与弹簧有关，将式（33）值代入式（34）得最佳弹簧下最佳阻尼为

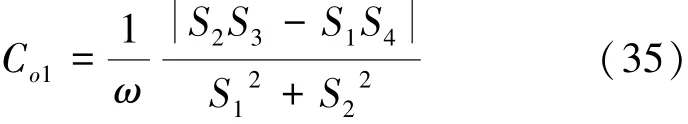
Ko1和Co1就称为最佳弹簧和最佳阻尼，将其代入式（31）即可求得最佳输出功率函数表达式为

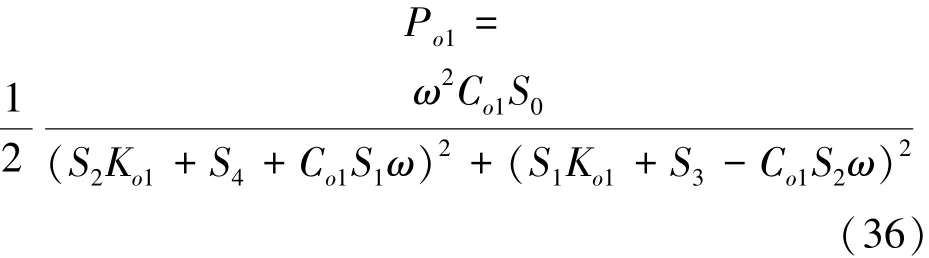
式（33）中，弹簧系数有可能出现负值，而负值弹簧没有物理意义，针对于无相变控制的波能装置，弹簧系数一般为一个固定的正值或者为0，当弹簧为一固定常值Kf时，式（34）所得最佳阻尼为

将式固定值Kf和式（37）代入式（31）得到固定弹簧最佳阻尼下波能装置吸收的最大功率为

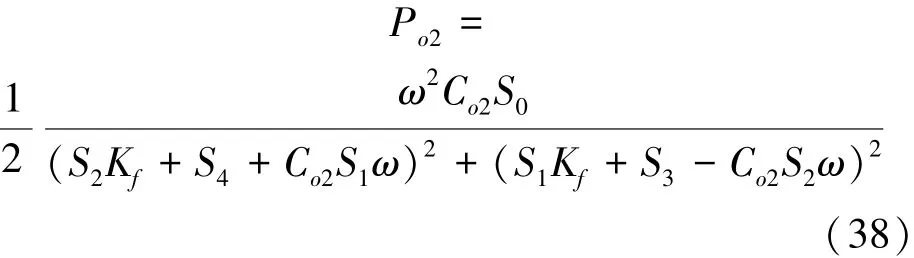
4 波浪激励力和水动力学系数计算

求解最佳弹簧、最佳阻尼和最大吸收功率等未知量，均需完成水动力学系数和波浪激励力计算。本文利用基于边界元方法的HydroStar软件对如图1中具有复杂形状波力直线发电波能装置建模并计算水动力学系数和波浪激励力。在一定水深情况下，求解装置在垂荡辐射速度势计算出的附加质量μ11、μ12、μ21、μ22和阻尼系数λ11、λ12、λ21、λ22（其中μ12＝μ21、λ12＝λ21，只需求μ12、λ12即可），由绕射速度势和入射波速度势计算出的波浪激励力Fez1、Fez2，然后使用Mathematica编程求解上述方程组。

4.1 方法验证

在使用软件HydroStar计算波能装置的水动力学系数和波浪激励力之前，需要验证HydroStar软件计算方法的准确性，本文按照Yeung［13］的算例选取相同参数用HydroStar进行了计算，并与Yeung的解析计算结果进行了比较（由于Yeung没有计算波浪力，因此仅与其计算出的附加质量和附加阻尼系数进行了比较。如图3，从图中可以看出2种方法计算出的附加质量和阻尼系数结果吻合得非常好，误差均在5%以内，这些误差还与从Yeung的纸质图中读取数据时存在的误差有关。因此认为使用HydroStar计算与解析方法计算结果一致，其计算结果可信。

图3 使用HydroStar计算的结果与Yeung的比较Fig.3 Comparison of the results calculated by HydroStar and Yeungs'

4.2 网格划分与计算结果

波能装置主要尺寸参数：h＝25 m、r1＝2.4 m、r2＝3 m、r3＝1.4 m、r4＝0.45 m、d1＝1.9 m、d2＝11 m、e1＝4 m、e2＝0.7 m、e3＝2 m、e4＝3.5 m。因计算时不涉及到装置的水线面以上部分，只需要在装置湿表面划分网格，水面浮体1的网格数为1 350，水下浮体2的网格数为2 100，模型的网格示意图如图4所示。计算时入射波波幅1 m，周期选为1～10 s，步长为0.1 s。由于该波能装置的轴对称性，计算时选择浪向角θ＝0。因装置受约束只作垂荡运动，航速选为0 m／s。据此计算出波能装置波浪激励力和水动力系数随入射波周期变化（见图5）。

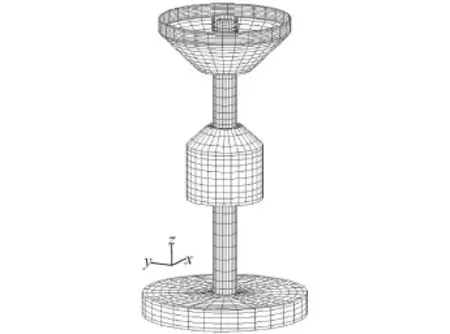
图4 波能装置网格示意图Fig.4 Mesh sketch of wave energy device

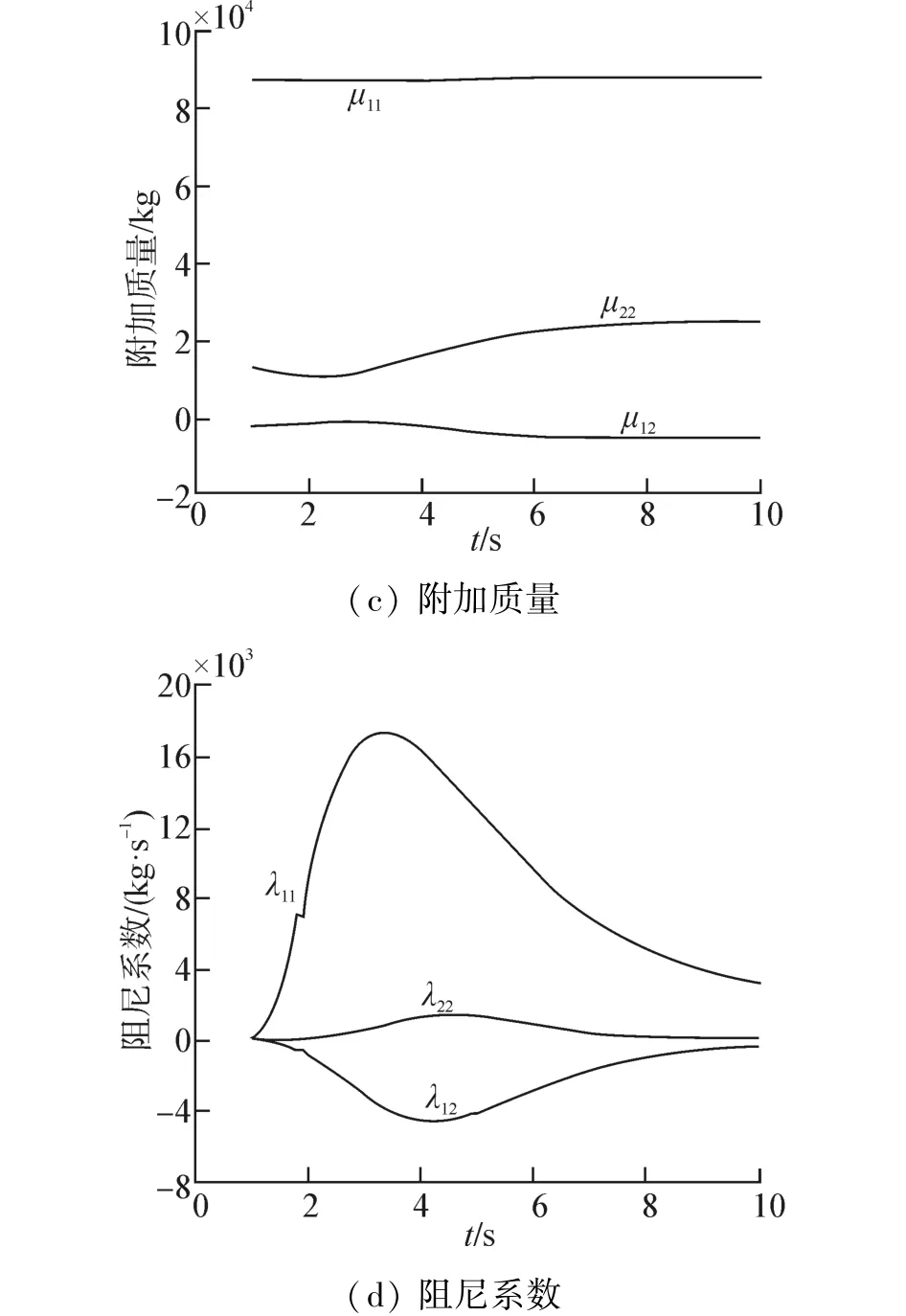
图5 波浪激励力和水动力学系数Fig.5 Wave exciting forces and hydrodynamic coefficient

5 数值计算结果分析

波能装置的俘获宽度比为

式中：Pi为射波功率，其计算公式为

式中：A为入射波波幅（波高的一半）；r1为浮子半径；ω为入射波频率，ω＝2π／T，T为入射波周期；k为波数；h为水深。

将所求得水动力学系数和波浪激励力代入式（20）、（25）～（29）、（33）、（35）～（40）可求得装置理论上的最佳弹簧、最佳阻尼、位移幅值响应、吸收功率和俘获宽度比。

图6描述了最佳弹簧、最佳阻尼随入射波周期的变化情况。图6中可看出，满足理论上最大功率所需弹簧系数在周期T＝3～7 s（在中国海域常见周期内）出现负值；在满足最佳弹簧条件下的最佳阻尼在周期6 s左右出现尖峰值达3 500 t／s左右。在实际工程中，负数可变弹簧很难实现，较多考虑选择固定值弹簧和可控制的粘性阻尼的波浪能装置，对于波力直线发电装置，阻尼可以通过改变直线电机特性和电阻负载大小来调节。以下将针对在常数弹簧的最优阻尼条件下，从波能装置的运动响应、吸收功率和俘获宽度比方面对波能装置结果进行分析。

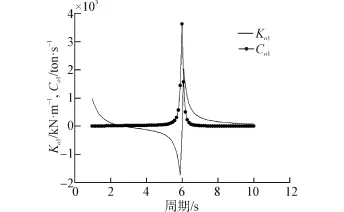
图6 最佳弹簧和最佳阻尼Fig.6 Optimal spring and optimal damping

与一般双自由度受迫振动系统相比，波能装置振动系统的特殊性主要表现在，波浪引起的静水刚度、附加质量、阻尼系数和波浪激励力随入射波周期不断变化。图7（a）为装置在弹簧为0条件下，最佳阻尼随周期变化曲线，与图6相比，其变化趋势基本一致，峰值出现的位置和大小变化较小，而峰值除外的阻尼比最佳弹簧条件下的阻尼值要大；图7（b）描述了波能装置的水上浮体1和水下浮体2的相对位移幅值随入射波周期变化，在无弹簧条件下，相对位移幅值随周期增大缓慢增大，当周期在2.7 s左右，幅值增至0.7 m左右（小于波浪幅值1 m），之后幅值缓慢减小趋于0.4 m，而最佳弹簧（7（b）中细实线所示）下的位移幅值在T大于6 s后无限增大；图7（c）为装置吸收的波浪能功率曲线，由图可知，理想状态的最佳弹簧和最佳阻尼下的功率Po1可无限增大，而无弹簧条件下的功率Po2在周期在6 s左右出现尖峰功率值达200 kW左右，此点也是最佳阻尼Co2发生尖峰值的点，除尖峰所在周期宽度5～7 s外，波能装置吸收的功率均小于50 kW，在图7（c）中，周期T＝3～7s内，最佳吸收功率均值达到55.6 kW；图7（d）描述了波能装置的俘获宽度比随波浪周期变化，该曲线在周期5.6～6.2 s内出现尖峰值达180%；除尖峰值外，曲线呈“几”字形状变化，其“几”字峰值周期宽度刚好在常见波况周期3～7 s内，其值均在40%左右。因此，增大俘获宽度比“几”字曲线的峰值周期宽度和提高峰值是设计高效率波浪能装置的关键。

根据以上计算结果，结合中国海域常见波况和直线电机特性（冲程、转换效率等）分析：在所计算波况范围内，波能装置的相对位移幅值较小且变化缓慢，较小的相对位移幅值和较低的相对运动速度都会导致直线电机损耗增大，转换效率降低，若装置加上适当弹簧，波能装置的低速小位移特性可能有所改善；通过优化装置形状，增大峰值出现的周期宽度，使波能装置在常见波况内的平均俘获宽度比进一步提高。

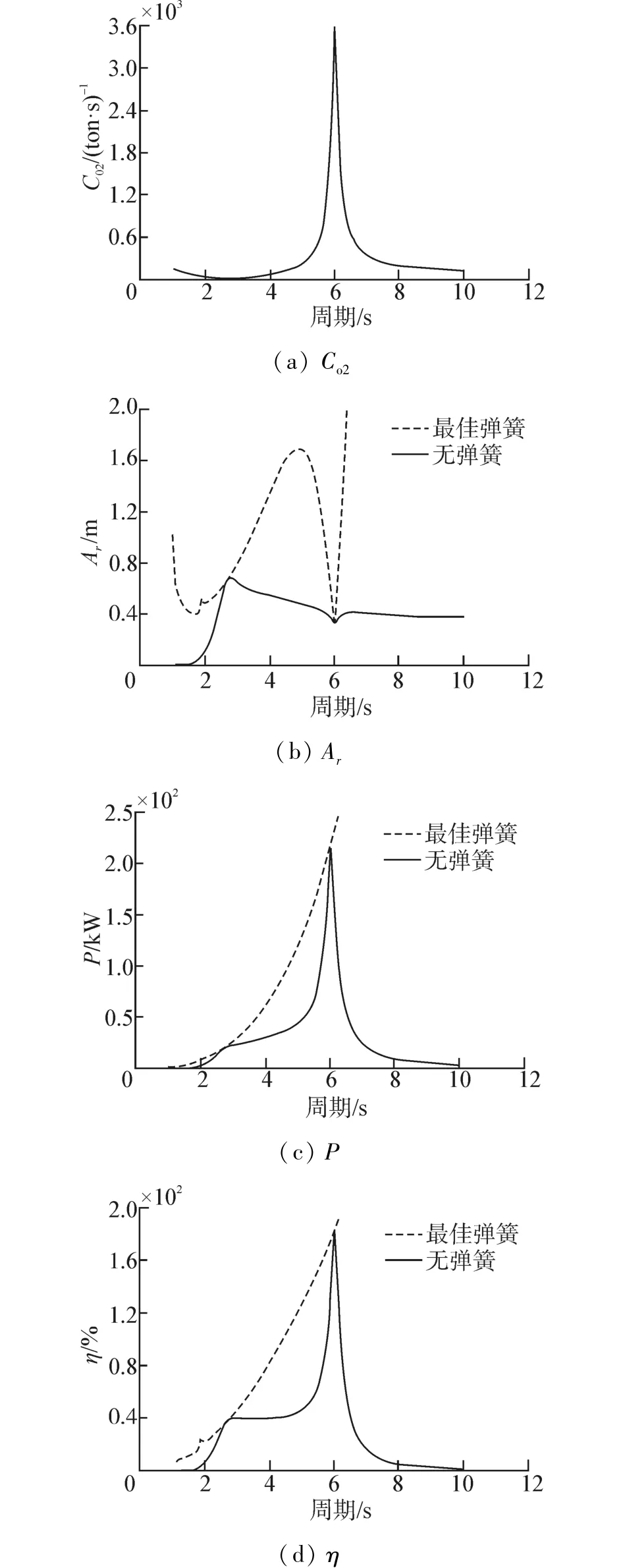
图7 最佳阻尼条件下的计算结果Fig.7 The calculation results in condition of optimal damping

6 结束语

本文以线性规则波理论为基础，采用粘性阻尼，建立漂浮直驱式波能装置的双自由度受迫振动方程，据此得出最佳弹簧和最佳阻尼下波能装置的最佳吸收功率函数表达式。数值计算表明：在满足装置理论上吸收最大功率的条件下，最佳弹簧系数在一定波况下出现了负值，因此该条件下装置的最大吸收功率不可能实现；在无弹簧、最佳阻尼条件下，装置的相对位移幅值变化缓慢、功率和俘获宽度比在给定入射波周期范围内出现峰值。文中所求解的最大俘获宽度比对波能装置设计和优化提供了理论依据和参考价值。

［1］FALCAO A F D O.Wave energy utilization：a review of the technologies［J］.Renewable and Sustainable Energy Reviews，2010，14（3）：899-918.

［2］RHINEFRANK K，AGAMLOH E B，VONJOUANNE A，et al.Novel ocean energy permanent magnet linear generator buoy［J］.Renewable Energy，2006，31（9）：1279-1298.

［3］LEIJON M，DANIELSSON O，ERIKSSON M，et al.An electrical approach to wave energy conversion［J］.Renewable Energy，2006，31（9）：1309-1319.

［4］ZHENG Y H，SHEN Y G，YOU Y G，et al.Hydrodynamic properties of two vertical truncated cylinders in waves［J］.Ocean Engineering，2005，32（3）：241-271.

［5］BERGGREN L，JOHANSSON M.Hydrodynamic coefficients of a wave energy device consisting of a buoy and a submerged plate［J］.Applied Ocean Research，1992，14（1）：51-58.

［6］TUNG C C.Total wave force on cylinder considering free surface fluctuation［J］.Applied Ocean Research，1996，18（1）：37-43.

［7］FALCAO A F D O，CANDIDO J J，JUSTINO P A P，et al.Hydrodynamics of the IPS buoy wave energy converter including the effect of nonuniform acceleration tube cross section［J］.Renewable Energy，2012，41：105-114.

［8］ERIKSSON M，ISBERG J，LEIJON M.Hydrodynamic modelling of a direct drive wave energy converter［J］.International Journal of Engineering Science，2005，43（17）：1377-1387.

［9］吴必军，盛松伟，张运秋，等.复杂圆柱型波能装置能量转换特性研究［J］.哈尔滨工程大学学报，2010，31（8）：1023-1028.WU Bijun，SHENG Songwei，ZHANG Yunqiu，et al.Wave-power conversion characteristics of a complex vertical cylinder［J］.Journal of Harbin Engineering University，2010，31（8）：1023-1028.

［10］VALERIO D.Optimization of wave energy extraction with the archimedes wave swing［J］.Ocean Engineering，2007，34：2330-2344.

［11］CANDIDO J J，JUSTINO P A P S.Modelling，control and Pontryagin maximum principle for a two-body wave energy device［J］.Renewable Energy，2011，36（5）：1545-1557.

［12］吴必军，王幸，刁向红，等.双圆柱形浮体波能装置双自由度响应及转换效率分析［J］.中国科学：物理学力学天文学，2013，43（8）：978-986.WU Bijun，WANG Xing，DIAO Xianghong，et al.Response and conversion efficiency of a wave energy device consisting of double cylindrical floats with two degrees of freedom［J］.Sci Sin-Phys Mech Astron，2013，43（8）：978-986.

［13］YEUNG R W.Added mass and damping of a vertical cylinder in finite depth waters［J］.Applied Ocean Research，1981，3（3）：119-133.

Optimization of complex-shaped wave energy linear power generation device

Lin Liqun1，2，3，WU Bijun1，2，WANG Xing1，2，WU Chunxu1，2，3，WANG Wensheng1，2
（1.Guangzhou Institute of Energy，Chinese Academy of Sciences，Guangzhou 510640，China；2.Key Laboratory of Renewable Energy and Gas Hydrate，Chinese Academy of Sciences，Guangzhou 510640，China；3.University of Chinese Academy of Sciences，Beijing 100049，China）

Aiming at the problem of energy conversion characteristics of a floating wave energy conversion（WEC）device，the double floating linear power generation WEC device was taken as a study object in this paper.The objective was to establish the forced double degree of freedom vibration equation of the complex-shaped WEC，in combination with the linear wave theory and viscous damping theory.Next，derive the expressions of the optimally absorbed power and relative displacement amplitudes of the WEC device with the best spring and the damping conditions.The hydrodynamic coefficient and wave excitation force of the complex-shaped WEC were calculated using the software HydroStar based on the boundary element method.Numerical calculations indicated that the optimal spring coefficient in a certain wave state becomes negative when the power absorption of the device is maximized.In the conditions of no-spring，the relative displacement amplitudes are smaller than the wave amplitudes and the peak values of absorbed power and capture width ratio appear in the range of given incident waves.

wave energy；linear generator；Hydrostar；optimal damping；optimal spring；capture width ratio

10.3969／j.issn.1006-7043.201308068

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201308058.html

TV139.2

A

1006-7043（2014）12-1529-07

2013-09-04.网络出版时间：2014-12-04.

国家自然科学基金资助项目（51276185，51079138）.

林礼群（1988-），女，研究助理，硕士；吴必军（1965-），研究员，博士生导师.

吴必军，E-mail：wubj＠ms.giec.ac.cn.