基于特征空间算法的非圆相干信源DOA估计

刁鸣，丁兆明，高洪元，李晨琬

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

基于特征空间算法的非圆相干信源DOA估计

刁鸣，丁兆明，高洪元，李晨琬

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

针对非圆相干信号的解相干问题，给出了一种新的特征空间算法（eigenspace-direction of arrival，ES-DOA）。利用信号源的非圆特性，虚拟地扩展了阵元个数，使阵列信息增至扩展前的两倍，对信号源数目的估计突破了M-1（M为阵元数）的限制；将信息量加倍后的协方差矩阵加以重构，给出一种新的特征空间算法进行解相干，最大限度地利用了噪声子空间与信号子空间的信息，避免了空间平滑思想的阵列孔径损失及最大似然算法运算量过大的问题；该方法还对信号源功率进行了估计，提高了对小能量信号的估计成功概率。仿真结果表明，该方法对波达方向估计具有很好的鲁棒性。

DOA估计；特征空间；非圆特性；相干信源；信号源功率；Toeplitz矩阵；MUSIC算法；小能量信号

随着BPSK、MASK、ASK、PAM等非圆信号在通信系统中的广泛应用，基于非圆信号的DOA（direction of arrival）估计技术已成为测向领域中的研究热点［1-2］。目前，针对非圆信号DOA估计的研究大多基于信号源完全独立的前提，而实际环境中的信号源往往不可避免地存在相干信号。最常用且相对成熟的解相干技术为Shan首次提出的空间平滑思想［3］，但由于空间平滑算法属于降维类算法，须对阵列进行划分，导致阵列孔径损失很大，检测相干源数目与子阵孔径大小成反比，对相干源数的估计极限仅为2M／3个［4-5］，且无法实现各信号源之间的完全解相干。基于空间平滑算法，文献［6］提出了模式空间平滑算法用于解决圆阵相干信号DOA估计问题。此外，最大似然方法［7］也是一种行之有效的解相干算法，其通过概率密度模型来估计相干信号，但运算量很大，且仍然无法检测信号源数目较多及多相干信源混合的情况，导致其实际应用的难度较大［8］。

文献［9］研究了基于特征空间DOA（ES-DOA）估计算法，其性能明显优于MUSIC等经典子空间类算法，并在信号解相干上取得了不错的效果。本文利用特征空间算法的解相干优势，结合非圆信号源的非圆特性，大幅度提升了对信源数目的估计能力［10］；在对阵列输出信号的协方差矩阵加以重构后，采用特殊的搜索函数进行谱峰搜索，最大限度地利用了噪声子空间与信号子空间的信息［9］，在不损失阵列孔径的同时，提高了对相干及强相关信号估计的有效性和优越性；该算法还结合了信号源的功率估计［11］，可对能量小的信号加以能量补偿，在低信噪比和小快拍数的情况下仍具有较好的稳健性。

1 估计信号的数学模型

1.1 非圆信号的数学模型

如图1所示，设有M个阵元的均匀线阵，阵元间距d为半波长λ／2，N个窄带信号分别从角度为θ1，θ2，…，θN入射到均匀线阵上，信号中包含相干或强相关信号。

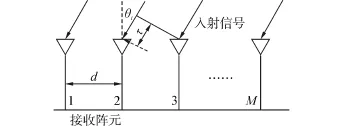
图1 均匀线阵示意图Fig.1 Equality line-antenna array

将M个阵元输出信号用矢量表示成X（t）＝［x1（t）x2（t）…xM（t）］，则第i个阵元输出的表达式为

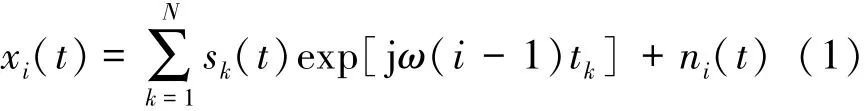
式中：sk（t）为入射信号，tk为第i个信源在相邻阵元间的时延，ni（t）为第k个阵元在t时刻的噪声和干扰。将式（1）写成矩阵形式为

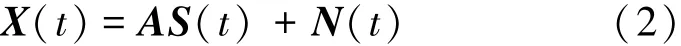
式中：

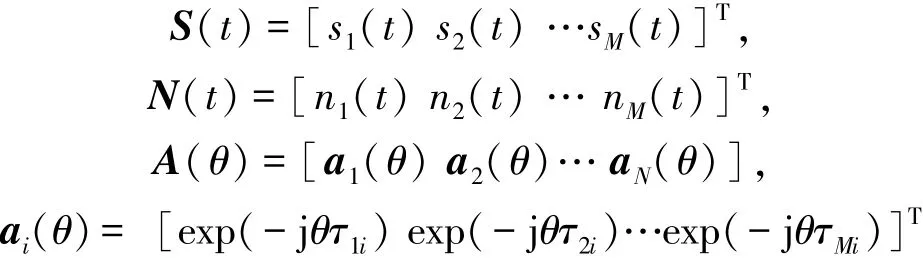
式中：θ＝2πf＝2πc／λ，c为光速，f为信号频率，λ为入射信号波长。通常接收信号的模型为

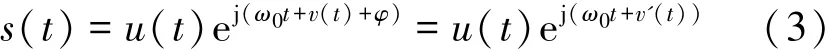
式中：u（t）为信号的幅度信息，v（t）为信号的相位信息，φ为信道附加信息，对于一般的圆形信号，通常将信道附加信息直接归入信号的相位信息之中，即φ对信号模型的构成不会产生影响。

而非圆信号为实值信号，即解调之后的信号为实数。所以为了使得信号模型更加接近实际情况而需考虑传输信道对信号的影响［12］，此时经过解调后的信号模型应改为

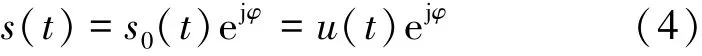
将式（4）代入式（2）中，可得非圆信号阵列接收数据模型为

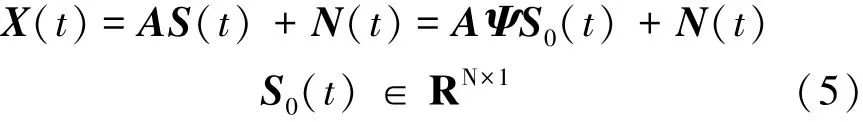
式中：Ψ＝diag（ejφ1，ejφ2，…，ejφN）是与每一个信号有关的信道附加相位组成的对角阵。

1.2 相干信号的数学模型

2个平稳信号si（t）、sk（t）间的相关情况用相关系数来定义，即

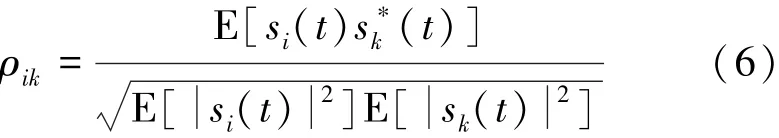
根据Schwartz不等式可知ρik≤1，定义当ρik＝1时，两信号相干。

由定义可知，当信号源存在相干关系时各信号之间只差一个复常量。假设有N个相干信号源，则有

式中：s0（t）可称为生成信源，αi即为第i个信号源si（t）相对于生成信源s0（t）的复衰减。将式（7）代入式（5）可得非圆相干信号的数学模型：

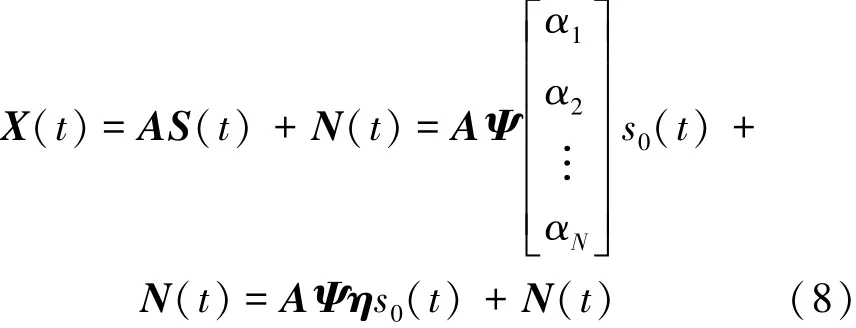
式中：η是由一系列复常数组成的N×1维矢量。

2 本文算法描述

设有一个复随机变量y，定义其均值为E［y］，协方差为E［yy*］，椭圆协方差（伪协方差）为E［y2］。若一个复随机变量的均值和椭圆协方差均为零，即E［y］＝0，则E［y2］＝0，则称此复随机变量为二阶圆性变量。若复随机变量不满足E［y2］的性质，则认为此复随机变量具有二阶非圆性［13］。事实上，对于非圆信号，二阶DOA算法中阵列输出的协方差矩阵和伪协方差矩阵分别为

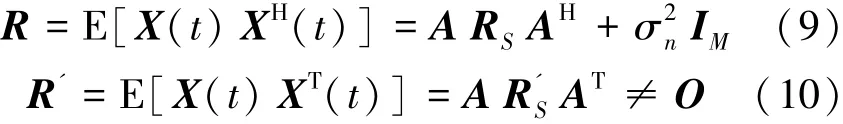
式中：RS＝E［S（t）SH（t）］，R＇S＝E［S（t）ST（t）］，为空间理想白噪声的噪声功率，IM为单位矩阵。

由于非圆信号的椭圆协方差不为零，即携带了信源信息，通过将接收数据和其共轭串联起来以增加数据维数的方式，可以虚拟地将阵元个数加倍，此时有

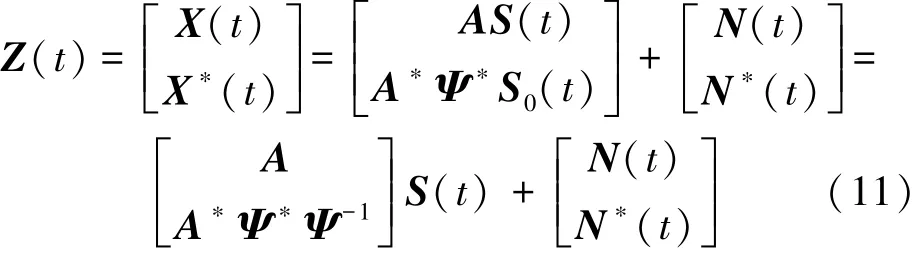
进而扩展后的数据协方差矩阵为

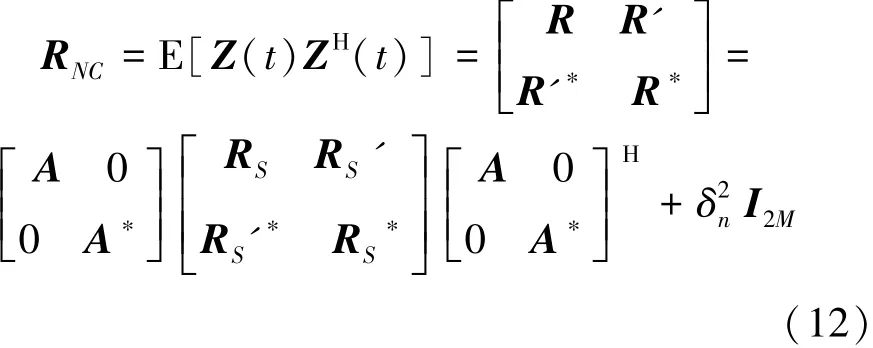
式中：R和R＇分别为阵列输出的协方差矩阵和椭圆协方差矩阵，R＝E［X（t）XH（t）］和R＇＝E［X（t）XT（t）］分别为信号矢量的协方差矩阵和椭圆协方差矩阵，RS＝E［S（t）SH（t）］，R＇S＝E［S（t）ST（t）］。

通过式（12）构造的阵列输出信号协方差矩阵由非圆相干信号组成，经典的解相干算法无法与非圆特性相结合。另外，在子空间类算法中如果信源中存在小能量信号，完成协方差矩阵特征分解后，小能量信号对应的特征值较小，很容易被强噪声干扰。本文将依据信号源功率的求解过程，用其功率的倒数对MUSIC算法的空间频率谱函数加权，以抑制噪声干扰。

首先对协方差矩阵加以重构，使其具备采用特征空间算法解相干的条件。设变换阵V为M阶交换阵，即

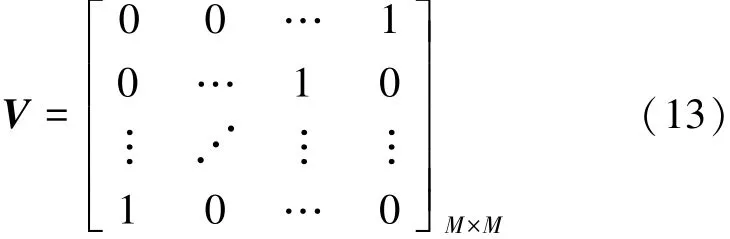
将协方差矩阵按如下方式重构：

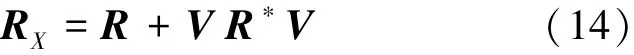
式中：R为Hermite矩阵，不具备Toeplitz矩阵的特性，而将R按式（14）修正后得到矩阵RX为Toeplitz矩阵。

依据信源功率的求解过程，定义一个新矩阵RA＝ASSHAH＝APAH＝USΛSUHS，其中P＝SSH，US为信号子空间，单取第i个信号处的导向矢量，进一步计算可得

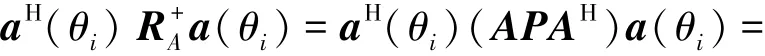
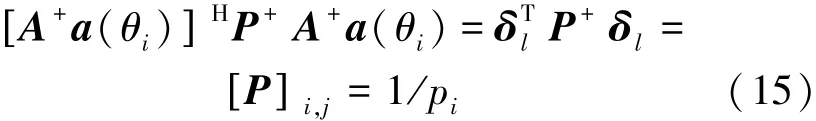
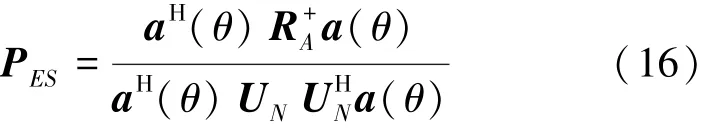
当信号搜索至信源处，即θ＝θi（i＝1，2，…，N）时，aH（θ）UNUHNa（θ）＝0，而aH（θ）a（θ）＝1／pi≠0，故PES的空间频率谱峰值在θ＝θi（i＝1，2，…，N）处。对接收信号协方差矩阵R重构后得到RX，使得谱峰搜索函数PES可应用于相干信号的DOA估计。

此外，本文定义的特殊空间谱函数不仅可以估计信号到达角，还可以估计信号源功率的大小。由式（15）可得，第i个信号的信源功率为pi＝1／aH（θi）R＋Aa（θi）

[ ]，可直接求出谱峰位置的功率值，便于对小能量信号的检测判断。

3 算法性能仿真验证

3.1 两类算法DOA估计的鲁棒性比较

假设有来波方向分别为－35°、20°和55°的3个相干BPSK信号，信噪比为－5 dB，均匀线阵的阵元数为8，阵元间距d＝λ／2，快拍数为500，分别采用本文算法和前后向空间平滑算法做100次Monte-Carlo实验。

由图2可得出，ES-DOA算法和空间平滑算法均可对非圆相干信号进行DOA估计，但ES-DOA算法的谱峰明显更加尖锐，且没有旁瓣和毛刺，表明该算法较空间平滑具有更好的鲁棒性。

假设有来波方向分别为－50°、－30°、－10°、10°、30°和50°的6个相干BPSK信号，其他条件同上，采用本文算法和前后向空间平滑算法对信号源进行100次Monte-Carlo实验，对比信号角度的真实值和估计值。

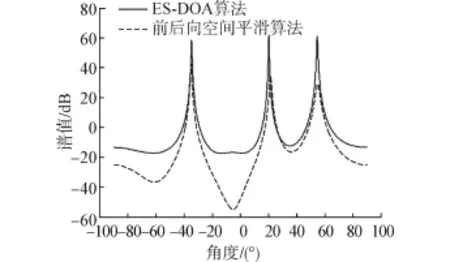
图2 两类算法谱峰搜索对比图Fig.2 Peak searching comparison of two algorithms

图3 分别为ES-DOA算法和空间平滑算法的“估计次数-到达角”对比图。通过对2张图的对比，可验证本文算法相对于空间平滑算法对非圆相干信号的估计具有更好的准确性。

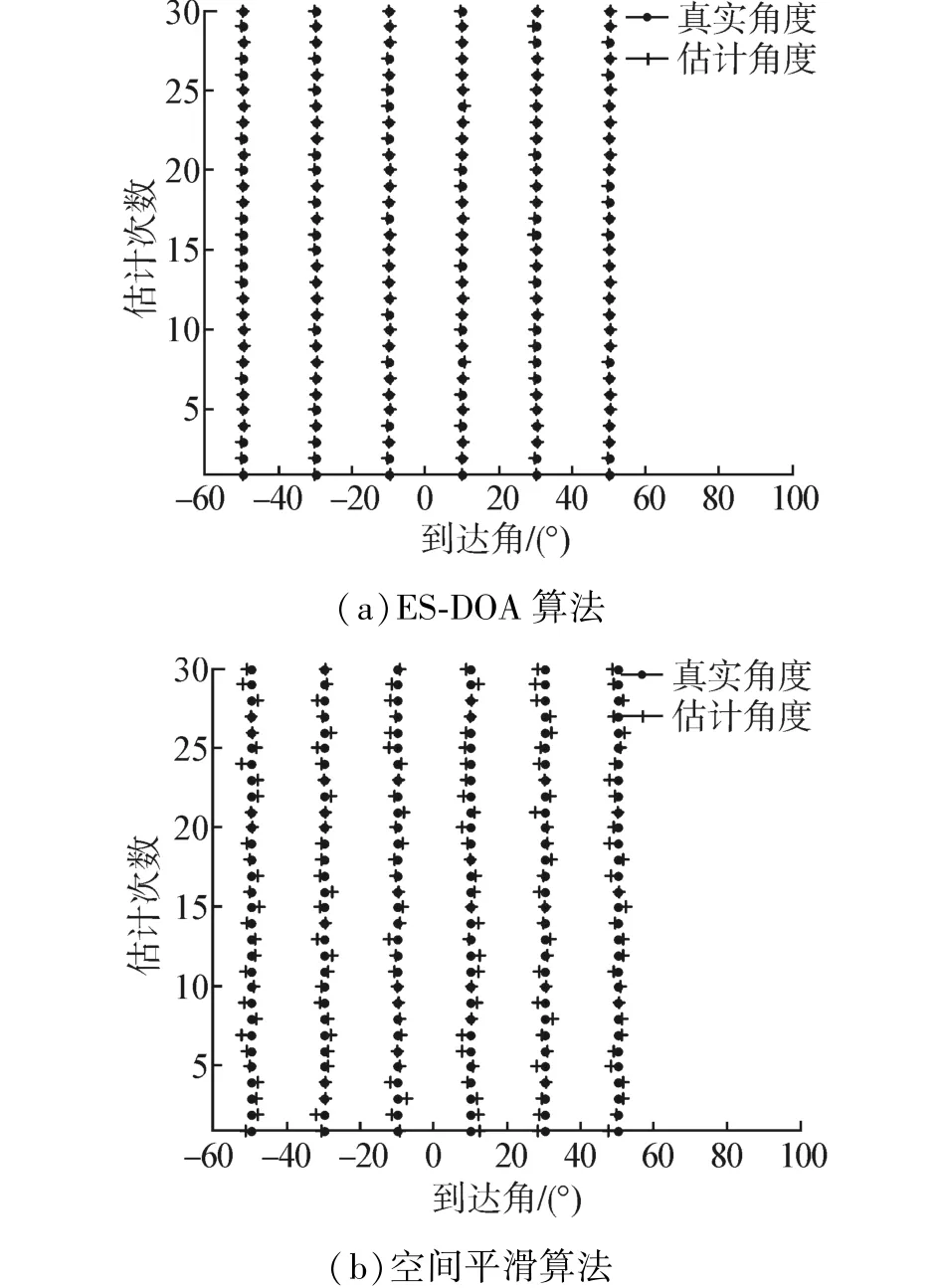
图3 估计次数－到达角Fig.3 Estimation times versus arrival angles

3.2 两类算法的解相干性能比较

假设有来波方向分别为－35°、－10°、20°和55°的4个相干BPSK信号，信噪比在－20～20 dB范围内由小到大渐变，均匀线阵的阵元数为10，阵元间距为d＝λ／2，快拍数为500，做100次Monte-Carlo实验，比较2种算法的估计成功概率和均方根误差。

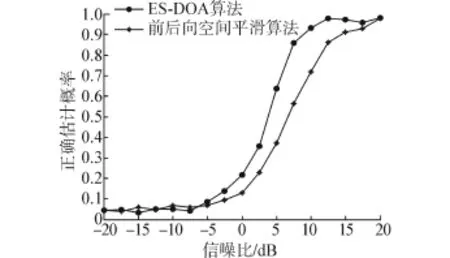
图4 估计成功概率Fig.4 Success probability of estimation

由图4可以看出，当信噪比低于－5 dB时，2种算法的估计成功概率大致相同，随着信噪比的增加，本文算法的成功概率明显高于空间平滑算法，说明估计相干信号时，本文算法的估计性能要优于空间平滑算法，同时也验证了所提算法的可靠性。由图5可以看出，2种算法的估计均方根误差都随着信噪比的增大而减小，当信噪比大于10 dB时，两者的估计均方根误差大致相同，当信噪比小于10 dB时，本文算法的估计均方根误差明显小于空间平滑算法，说明本文算法适用于低信噪比信号的估计，估计性能与空间平滑算法相比更加稳定。

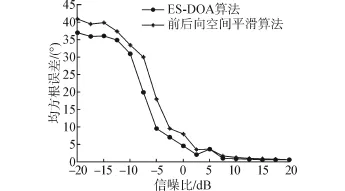
图5 估计均方根误差Fig.5 Mean square error of estimation

3.3 信源数接近阵元数情况下的估计性能对比

假设有来波方向分别为－45°、－5°、20°、55°和80°的5个相干BPSK信号，信噪比为－5 dB，均匀线阵的阵元数为8，阵元间距为d＝λ／2，快拍数为500，分别采用本文算法和前后向空间平滑算法做100次Monte-Carlo实验。

图6为相对于阵元数信号源数目较多的情况下2种算法对相干BPSK信号的谱峰搜索图，从图上可明显得出，本文算法仍可有效地估计出各信号角度，只是80°来波方向信号的估计精度稍差；而空间平滑算法只能估计出2个信号角度，基本失效，表明本文算法适用于信源数目较大时的估计情况。

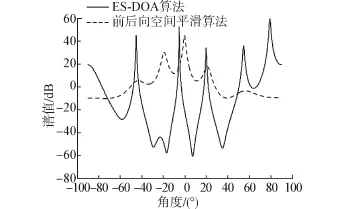
图6 多信号源情况下谱峰搜索对比图Fig.6 Peak searching comparison in multi-signal sources

3.4 信号源功率估计的性能检验

假设有来波方向分别为15°、30°和55°的3个相干BPSK信号，均匀线阵的阵元数为8，阵元间距为d＝λ／2，信噪比从0～20 dB递增，快拍数分别取200、300、500和1 000，做50次Monte-Carlo实验，验证本文算法对信号源功率的估计性能。

定义均方误差为PMSE＝（pi－pie）2，其中pi和pie分别为第i个信号功率的真实值和估计值。由图7可以看出，随着信噪比的增加，所得的均方误差越来越小，本算法具有较好的信源功率估计能力，且估计性能随着快拍数的增大而增大。

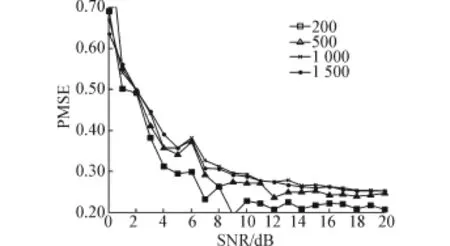
图7 信号源功率估计性能Fig.7 Estimation performance of signal power

4 结束语

本文以BPSK调制信号为例，结合非圆信号的自身特性，给出了一种针对非圆相干信号的特征空间算法（ES-DOA）。该算法可扩展阵列信息，适用于多信号源数目的估计情况，通过将阵列输出信号的协方差矩阵重构为Toeplitz矩阵，使其具备谱峰搜索的前提条件，避免了现有的解相干算法阵列孔径损失严重、计算量较大等问题。此外，该算法还结合了信号源功率，便于对能量较小的信号进行能量补偿，试用的噪声环境更广。

该算法利用了非圆信号特性，扩展了阵列孔径，可以估计更多的信号源，提高了DOA估计性能；算法结合了信号源的功率估计，可以适用于估计能量小，低信噪比的相干信号；通过与前后向空间平滑技术进行对比，仿真结果证实了该算法具有较高的精度和较强的鲁棒性。

［1］刁鸣，安春莲，万文龙.非圆信号的四阶累积量测向新方法［J］.哈尔滨工程大学学报，2012，33（1）：112-116.DIAO Ming，AN Chunlian，WAN Wenlong.A novel direction finding algorithm for noncircular signals based on fourth-order cumulants［J］.Journal of Harbin Engineering University，2012，33（1）：112-116.

［2］LIU Aifei，LIAO Guisheng，XU Qing，et al.A circularitybased DOA estimation method under coexistence of noncircular and circular signals［C］／／2012 IEEE International Conference on Acoustics，Speech and Signal Processing（ICASSP）.Kyoto，Japan，2012：2561-2564.

［3］SHAN T J，WAX HAN M，KAILATH T.On spatial smoothing for direction-of-arrival estimation of coherent signals［J］.IEEE Transactions on Acoustic，Speech and Signal Progressing，1985，33（4）：806-811.

［4］WILLIAMS R T，SUREBDA P，MAHALANABIS A K，et al. An improved spatial smoothing technique for bearing estimation in a multipath environment［J］.IEEE Transactions on Acoustics，Speech and Signal Progressing，1988，36（4）：425-432.

［5］朱圣棋，廖桂生，李海，等.基于数据矩阵的非圆相干信号完全解相关算法［J］.系统工程与电子技术，2009，31（1）：21-24.ZHU Shengqi，LIAO Guisheng，LI Hai，et al.DOA eatimation of coherent signals based on data matrix［J］.Systems Engineering and Electronics，2009，31（1）：21-24.

［6］韩晓东，刁鸣.冲击噪声背景下均匀圆阵相干信源的DOA估计［J］.应用科技，2012，39（1）：35-38.HAN Xiaodong，DIAO Ming.DOA estimation of uniform circular array and coherent sources in an impulsive noise environment［J］.Applied Science and Technology，2012，39（1）：35-38.

［7］王布宏，王永良，陈辉.相干信号源波达方向估计的广义最大似然算法［J］.电子与信息学报，2004，26（2）：225-232.WANG Buhong，WANG Yongliang，CHEN Hui.Generalized maximum likelihood algorithm for direction-of-arrival estimation of coherent sources［J］.Journal of Electronics＆Information Technology，2004，26（2）：225-232.

［8］庞伟正，高洪元，王艳丽.基于粒子群优化算法的相干信源波达方向估计［J］.哈尔滨工程大学学报，2006，27（3）：453-456.PANG Weizheng，GAO Hongyuan，WANG Yanli，et al.Estimating direction-of-arrival of coherent source based on particle swarm optimization algorithm［J］.Journal of Harbin Engineering University，2006，27（3）：453-456.

［9］ZHANG Xiaofei，LYU Wen，SHI Ying，et al.A novel DOA estimation algorithm based on eigen space［C］／／IEEE 2007 International Symposium on Microwave，Antenna，Propagation，and EMC Technologies for Wireless Communications.Hangzhou，China，2007：551-554.

［10］郑春弟，冯大政，雷革.一种利用非圆信号特点的实值DOA估计算法［J］.数据采集与处理，2009，24（2）：193-197.ZHENG Chundi，FENG Dazheng，LEI Ge.DOA Estimation algorithm for non-cicular sources using real-value algorithm［J］.Journal of Data Acquisition and Processing，2009，24（2）：193-197.

［11］崔波，罗景青.最小冗余线阵的ES-DOA估计算法研究［J］.信号处理，2010，26（7）：1016-1020.CUI Bo，LUO Jingqing.Study on ES-DOA estimation algorithm of minimun-redundancy linear arrays［J］.Signal Processing，2010，26（7）：1016-1020.

［12］HASSEN S B，BELLILI F，SAMET A，et al.DOA estimation of temporally and spatially correlated narrowband noncircular sources in spatially correlated white noise［J］.IEEE Transactions on Signal Processing，2011，59（9）：4108-4121.

［13］HUANG Z T，LIU J，ZHOU Y Y.Performance analysis of MUSIC for non-circular signals in the presence of mutual coupling［J］.IET Radar，Sonar and Navigation，2010，4（5）：703-711.

Estimating direction of arrival of non-circular coherent signals based on ES-DOA estimation algorithm

DIAO Ming，DING Zhaoming，GAO Hongyuan，LI Chenwan
（College of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China）

A new eigenspace-direction of arrival（ES-DOA）de-correlation algorithm is presented to estimate the direction of arrival of non-circular coherent signals.It takes advantage of non-circular characteristics of the signal source，virtually extends the number of the

array elements and doubles the array information compared with the information before extension.This makes the estimation of signal source number break through the maximum M-1（with M representing the number of sensor elements）.Restructure the covariance matrix in which the amount of information has been doubled，and then do the de-correlation by the proposed ES-DOA algorithm.The new algorithm can make use of the information of signal subspace and noise subspace to the largest extent，and avoids the problem of array aperture loss caused by the spatial smoothing algorithm and the large amount of calculation caused by the maximum likelihood algorithm.Besides，the proposed ES-DOA algorithm can also be used to estimate the power of signal source，which can improve the probability of success in the estimation of low power signals.The simulation results indicated that the method is effective and robust in DOA estimation.

DOA estimation；eigenspace；non-circular characteristic；coherent signals；signal power；Toeplitz matrix；MUSIC algorithm；low power signal

10.3969／j.issn.1006-7043.201310073

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201310073.html

TN911

A

1006-7043（2014）12-1559-05

2013-10-25.网络出版时间：2014-12-04.

国家自然科学基金资助项目（61102106，61102105）；中国博士后基金资助项目（2013M530148）.

刁鸣（1960-），男，教授，博士生导师.

刁鸣，E-mail：diaoming＠hrbeu.edu.cn.