非线性铰接双浮体波能转换器的能量捕获特性研究

周 潇，张海成，施奇佳，徐道临，邹伟生

（1.湖南大学机械与运载工程学院，长沙 410000；2.长沙理工大学水利工程学院，长沙 410114）

0 引 言

随着经济和社会的发展，人类对能源的需求越来越大。为了解决能源短缺问题，寻找替代的可再生能源已经成为全球共识[1-2]。在可再生能源中，波浪能因具有能量密度高[3]、连续性好[4]等优点而受到人们的广泛关注。

到目前为止，已经有超过1000种波能转换技术获得了专利[5]。这些装置中，铰接浮体波能转换器（WEC）由于无需依赖固定约束结构[6]，所以具有相对较高的海域适应性。铰接浮体波能转换器主要利用相邻模块的相对转动来驱动发电系统，使波浪能转化为电能。在国外，早期关于铰接浮体波能转换器的著名研究是由Haren 等[7]开展的，他们对一些浮体的轮廓进行了全面的理论分析，研究了浮体几何参数对波能捕获效率的影响规律。海蛇型波能转换器（Pelamis WEC）[6]是铰接浮体波能转换器最成功的应用之一。Pelami波能转换器是一种半潜式蛇状圆柱形装置，模块间由铰链接头连接，使相邻模块能够在关节周围进行相对的纵摇和艏摇运动，以捕获波浪能量。除了上述的代表性应用外，基于铰接模块波能转换器的原理还有一些潜在的应用。一些学者提出将铰接波能转换器与浮式防波堤相结合，组合成消波吸能复合结构物[8]。同时，利用海洋空间和波浪能的多功能海洋平台[9]所附连的铰接减摇结构[10-12]是减少平台水弹性响应和增强波能吸收的良好选择。虽然铰接浮体波能转换装置在海洋技术方面有着巨大的应用潜力，但仍然未得到大规模的工程应用[13]，其中制约传统线性波能转换器最重要的问题是捕获效率较低和频带窄。波能装置的转换效率与许多因素有关，包括入射波频率、波能装置形状、吃水深度、重心以及能量转换系统的参数等[14]。众所周知，线性波能转换器为了达到较好的波能捕获效率通常设置为特定频率进行谐振。由于海浪的主导频率可能随时间而变化，使其偏离系统的设计频率，从而导致线性波能转换器在效率方面可能不佳。此外，真实的波浪是具有波谱特征的不规则波，由于线性波能转换器较窄的波能捕获频带同样不能很好地捕获非规则波中各个频率分布下的能量，从而影响总体捕获效率。为了提高波能转换器的捕获效率，很多研究者已经进行了多项工作。一些学者[15-16]致力于通过优化浮体模块的形状和尺寸，进而优化铰接浮体波能转换装置的波能转换效率。他们针对浮体横截面、浮体半径等结构几何参数方面进行了研究，但是发现通过结构改进提高效率的效果有限。另一方面，对于铰接波能转换器来讲，要捕获低频长波的能量，需要浮体尺度与波长匹配（共振时）才能有效，这就需要设计尺度较大的浮体来吸收波浪中的长波能量，这对于结构的安全性是个极大的挑战。也有学者采用主动控制技术来提高波能转换器的效率。闭锁控制[17]及最优控制策略[18]等方法已在多个自由度（degree of freedom，DOF）波能转换器中得以实现。数值结果表明，控制方法对提高规则和不规则波中波能转换器的性能是有效的。但值得注意的是，控制器的性能必须依赖于入射波的所有信息[19]，然而，对于真实的波况，波面信息的预测是复杂而困难的[20]。此外，主控控制方法还存在可靠性低、维护难等一些实际问题。

提高波能转换装置效率的另一个途径是利用非线性捕获机制[21]。近年来，已有学者提出了许多基于非线性刚度或阻尼机制的能量捕获装置，其在机械振动、微型机电系统[22-23]的能量采集领域得到了广泛的研究与应用。对于波能捕获系统，Zhang 等[24-25]最早将由两个对称斜弹簧组成的经典负刚度机构引入到点吸收波能转换器中，研究了负刚度机构对点吸收波能转换器的波能捕获特性，数值结果表明，附加合适参数的负刚度机构后能显著提高波能吸收效率，扩大捕获频带宽度。基于相同的原理，磁弹簧[26-27]和气动弹簧[28]形成的其它非线性负刚度机构也应用于点吸收式波能转换器。其基本原理均是通过附加负刚度机构从而减小系统的等效固有频率，同时附加的负刚度机构与浮子的静水恢复力形成双稳态系统，由于双稳态系统的阱间跳跃机理可放大浮体的运动幅值，从而有效提高波能捕获效率。与上述负刚度机制不同，Younesian 和Alam[29]提出了一种由两个倾斜的刚性连杆和两个倾斜的线性弹簧组成的非线性负刚度机构，并将其应用于点吸收波能转换装置中，该装置与浮子的静水恢复力耦合可形成多稳态系统。数值结果表明，与传统的非线性负刚度机制相比，新型非线性负刚度装置还可以通过减小稳态间的势垒，从而提高非线性波能转换器的稳定性。值得注意的是，上述研究都仅涉及点波能转换器，且均理想地考虑浮体仅沿垂荡方向运动。然而，在实际海况下，浮式波能捕获装置一般都具有多个运动自由度，应考虑多自由度耦合对浮体系统的影响，所以多模块浮体结构的一般分析较为复杂。由于多自由度之间的耦合效应和能量交换，多自由度波能转换器中使用的非线性负刚度装置的机理尚不明确，需进一步深入研究。另一方面，针对海洋复杂环境，如何设计易于海洋波能捕获装置海上安装实施的简易负刚度机构也是值得关注的。

本文针对铰接浮体波能转换器能量捕获效率低、捕获频带窄的技术瓶颈，提出一种简洁紧凑的非线性负刚度机构，并对其开展动力学建模以及能量捕获特性研究。首先，提出负刚度机构的概念设计，其由一简单的拉伸弹性元件组成。其次，基于Cummins方程建立铰接两浮体系统的非线性运动控制方程。非线性控制方程里面的卷积积分项使用状态空间模型代替，以加快其计算速度。最后，在数值模拟中，针对铰接两浮体波能转换器来研究能量吸收和动力学响应的特性，进行数值验证，以验证模型的正确性。最后开展非线性铰接波能转换器的波能捕获特性和系统动力学响应特性研究，揭示波能转换器效率提升的机制，研究系统参数对波能捕获效率的影响规律。

1 铰接双浮体非线性波能转换器的动力学模型

1.1 非线性波能转换器的结构概念设计

图1 显示了铰接双浮体波能转换装置。浮体形状设计为椭圆形，波能转换器的相邻浮体通过两个铰链和一个非线性能量捕获系统相连。其中，能量捕获系统主要由液压系统、非线性刚度机构和能量转换系统组成。液压缸的一端与活塞杆相连接，另一端通过油管与能量转换装置相连接。当浮体受到波浪激励作用时，两个浮体将产生绕铰链的相对纵摇运动，推动活塞做功，最后通过能量转换装置进行发电。非线性能量捕获系统的等效力学模型如图2 所示（侧视图）。其中，能量转换系统可表征为具有线性阻尼系数的阻尼器c0。本文提出的非线性刚度机构可表征为一个具有刚度系数k0的线性弹簧，线性弹簧的原长为L0，当两相邻浮体没有相对旋转时，该弹簧处于预拉伸状态，即此时弹簧两端铰接点之间的距离δ＞L0。对于施加此非线性刚度机构的两模块铰接系统，当两浮体发生小角度的相对转动时（即转角始终保证弹簧处于拉伸状态），弹簧力对浮体绕铰链相对转动产生负刚度的作用效果，从而降低纵摇自由度方向的系统等效刚度。

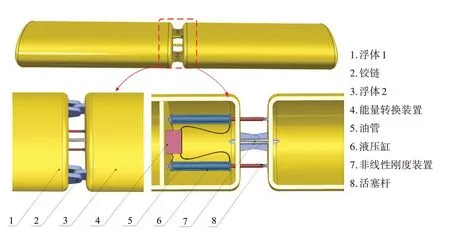
图1 非线性铰接双浮体波能转换器结构示意图Fig.1 Structure diagram of wave energy converter with nonlinear hinged double floating body

图2 非线性能量捕获系统等效力学模型Fig.2 Equivalent mechanical model of the nonlinear power take-off system

1.2 波能转换器的运动控制方程

本文仅考虑顶浪方向的波浪激励，且每个模块只考虑纵荡、垂荡和纵摇三个运动自由度。首先，我们建立两套参考坐标系，如图3 所示。其中全局坐标系（OXZ）的（X-Z）平面垂直于未扰动自由液面，且Z轴指向向上。另一个是以浮体m的质心为原点建立的局部坐标系（xm，zm），其中水平轴xm轴指向浮体的纵向，zm轴竖直向上。

图3 双浮体系统坐标系示意图Fig.3 Coordinate systems for two-module system

由Cummins方程[30]可知，非线性波能转换器的时域运动控制方程可写为

公式（1）等号左侧的三项FC、FP、FN分别表示铰接连接器、能量转换装置阻尼器和非线性刚度机构产生的力矢量。它们将在下文中逐步推导出。

对于刚性铰接连接器，传统可采用拉格朗日乘子法[32-33]建立其位移约束数学模型，并与浮体运动微分方程联立组成铰接浮体的微分代数控制方程组。若系统中存在非线性特性，系统运动控制方程将变为非线性微分代数方程组，该方程数学上求解相对较困难。为了避免求解非线性微分代数方程组，本文采用柔性铰接连接器刚化模型来模拟刚性连接器模型，即将铰接连接器模拟为具有弹性的柔性铰接连接器，后将连接器刚度设置为相对较大值来模拟刚性铰接连接器。以下模型推导时，由于只考虑顶浪的情况，不考虑相邻浮体的相对艏摇运动，可假定仅在浮体的纵向中心线安装一个铰接连接器。

将连接器考虑为柔性连接器时，两个浮体上铰链接头的两个连接点的位移矢量可以表示为

式中，Tm(m=1,2)表示变换矩阵，其一般形式[34]可定义为

其中，(xcm,zcm)表示第m个模块质心的全局坐标，(x0m,z0m)表示所连接浮体的连接点的坐标。

因此，安装在两个浮体之间的连接器变形矢量可以表示为

浮体2对浮体1的连接器载荷可以写为

式中，Kc表示铰接连接器的刚度矩阵，可表示为

其中，kx和kz分别表示纵向和垂向刚度系数，且本文中令kx=kz=kc。

考虑作用力与反作用力的关系，浮体2上连接器载荷可表示为F21=-F12。

由连接器变形而产生的作用力可以通过变换矩阵将其施加在两个浮体的质心上，有

下面进一步推导引入的非线性能量捕获装置的力学模型。基于浮体小旋转角度的假设，由图2力学模型的几何关系可知，能量捕获系统的两个铰接点之间的相对位移可以表示为

式中，r0为铰接点到铰链连接器中心的垂直距离（如图2所示）。

能量捕获系统作用在浮体1上的阻尼力矩Mp可表示为

对于非线性刚度机构，当两浮体发生相对纵摇运动时，其运动简图如图4所示。

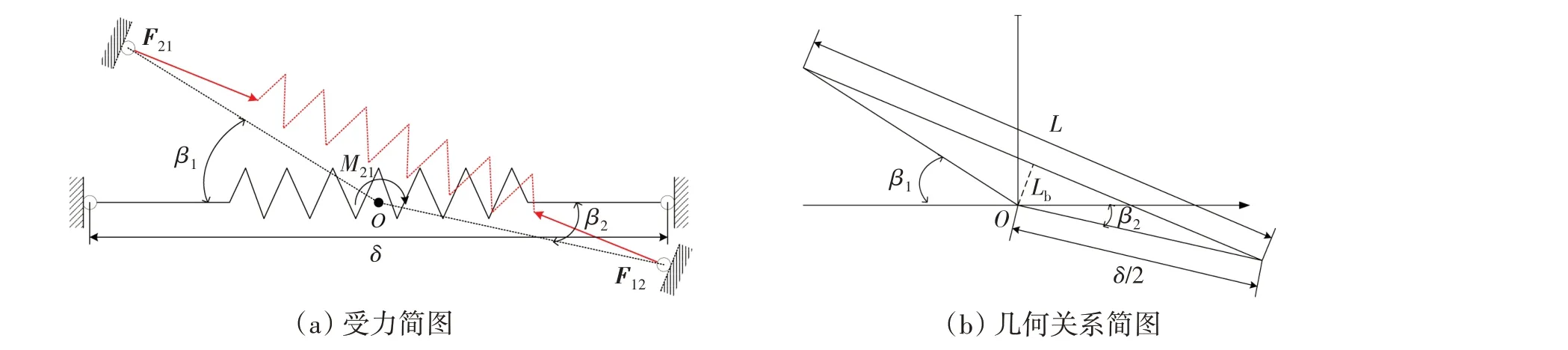
图4 系统运动简图Fig.4 System motion diagram

当两浮体运动到图4（a）的位置时，由图4（b）中几何关系可得的任意时刻弹簧长L可表示为

基于胡克定律，浮体1受到的弹簧力可表示为

弹簧力对铰接点的力臂Lb为

考虑作用力与反作用力的关系，浮体2 上能量捕获系统产生的阻尼力矩为M'p=-Mp，弹簧力对浮体2的力矩为M'n=-Mn，即能量捕获系统和非线性机构的力向量可以写成

1.3 状态空间模型

式（1）中表示辐射力的卷积积分项在数值求解中会消耗大量的计算时间。已有研究表明，采用状态空间模型替换卷积积分项比直接求解卷积积分快近八倍[31]。本文同样采用状态空间替代模型求解卷积积分项。令式（1）中的卷积积分项为

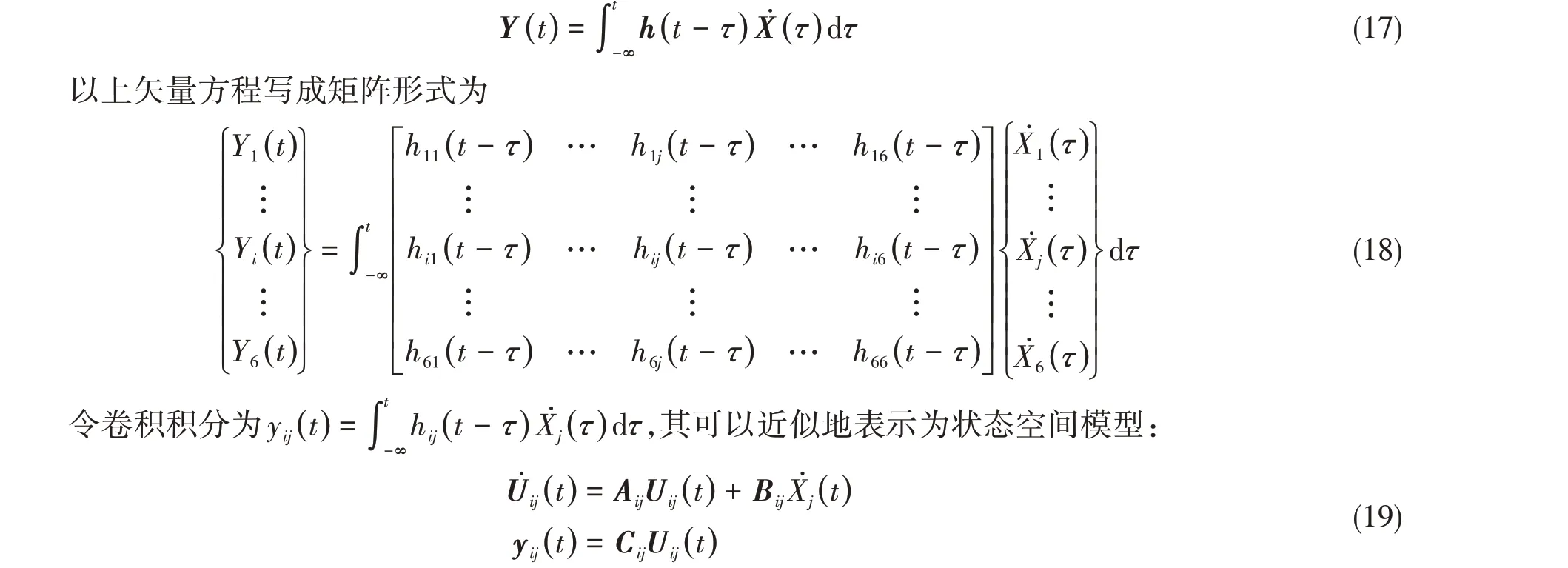
式中，Uij是由状态空间模型引入的状态矢量，其维度取决于状态空间模型的识别维度。

状态空间模型中关键的问题是确定系数矩阵Aij，Bij和Cij。本文采用基于水动力系数的频域识别方法[31]。由傅立叶变换可知，

1.4 波能捕获模型

基于数值模拟获得铰接浮体波能转换器的动力学响应后，可由式（10）的阻尼力矩做功来计算波能转换器捕获能量的平均功率：

式中，T0是波浪周期的整数倍。

根据线性波浪理论，有限水深规则波的单位波前的入射波功率可以通过下式[36]计算：

式中，g是重力加速度，A为波幅，ρ为水的密度，cg表示波的群速度，其可以通过下式求得：

其中，d表示水深，k表示波数且满足色散关系ω2=gktanh(kd)。

捕获宽度比被广泛用于评估波能转换器的性能，其可以通过下式表示：

2 非线性波能转换器的能量捕获特性

2.1 仿真参数

本文以两个相同椭圆浮体组成的铰接多浮体波能转换器为例[33]进行数值仿真研究，模型如图5所示。其中浮体的几何参数采用文献[33]已优化的结果。表1给出了该波能转换器的主要参数值，其中每个浮体的惯性参数可基于均质材料的假设来计算获得。

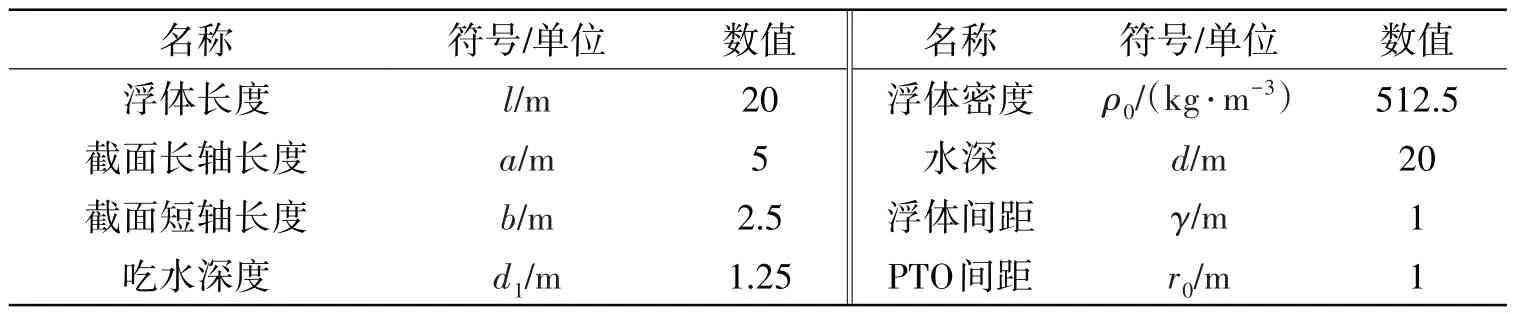
表1 两模块波能转换器的主要参数Tab.1 Main parameters of two-module wave energy converter

图5 浮体模型尺寸示意图Fig.5 Model design dimensions of the modules

为了计算结果不失一般性，引入以下无量纲数：

式中，kβ表示浮体纵摇方向的静水恢复刚度系数，即为ks的第三个对角线元素。

2.2 数值验证

为了验证连接器模型和卷积积分项替换的正确性，下面将不考虑非线性刚度机构的结果与文献[33]进行对比，选取线性系统峰值频率ω*=1.80，波浪幅值A*=0.2，拉伸弹簧无量纲刚度k*0=0。为了表征刚性铰接连接器，我们选取相对较大的无量纲连接器刚度为k*c=1。使用龙格库塔方法求解系统的时域动力学方程（1），并将其获得的波能捕获宽度的结果与参考文献[33]中频域方法获得的相应结果进行对比，如图6 所示。从图中可以看出，该方法的结果与郑等人[33]的结果一致，表明本文中推导的铰接力学模型和状态空间模型中参数识别的正确性。对比同时说明，连接刚度k*c=1 可等效表征刚性铰接连接器，下文中铰接连接器刚度均取该值。

图6 系统能量捕获宽度比随阻尼系数变化验证图（入射波频率ω*=1.80，连接器刚度k*c=1，波浪幅值A*=0.2，弹簧刚度k*0=0）Fig.6 Numerical verification of system capture width ratio under different damping coefficients (Incident wave frequency ω*=1.80,connector stiffness k*c=1,wave amplitude A*=0.2,spring stiffness k*0=0)

2.3 非线性铰接浮体波能转换器的静力学特性分析

波能转换系统的刚度直接影响系统的固有频率，进而影响系统的波能捕获效率，下面通过波能转换器的势能研究非线性波能转换器的刚度特性。不考虑重力势能，非线性铰接浮体波能转换器纵摇自由度弹性力（静水恢复力和附加非线性刚度机构）的势能可以写成

为了更加直观地了解非线性刚度机构对于铰接浮体波能转换器的静力学特性的影响规律，首先给出线性系统即不附加非线性刚度机构的势能图像，如图7所示。

图7 线性系统势能云图（阻尼系数c*0=0.01，波浪幅值A*=0.2，弹簧刚度系数 k*0=0）Fig.7 Potential energy surface of linear system (Damping coefficient c*0=0.01, wave amplitude A*=0.2, spring stiffness k*0=0)

图8 给出了不同非线性系统参数下浮体系统纵摇自由度方向的势能变化云图。将非线性刚度机构引入铰接多浮体波能转换器时，系统的纵摇势能曲面由图7 的圆形等值线变成如图8（a）、（b）、（d）所示的具有椭圆形等值线的形状，当附加非线性机构的刚度系数k*0增大，同时参数α较小时，即参数如图8（c）所示时，非线性刚度机构提供的纵摇扭转负刚度越来越大，负刚度项对于势能的影响越来越大，势能井将会由图8（a）、（b）、（d）所示的单井变成图8（c）所示的位于二四象限的双井的哑铃型云图。此时在浮体静水平衡位置处，附加负刚度机构提供的负刚度值大于静水恢复正刚度，导致系统在静水平衡位置处于不稳定的负刚度现象，所以系统出现双井势能曲面，此时系统存在两个稳定平衡点和一个不稳定平衡点。

图8 各个参数下纵摇自由度方向的势能变化（阻尼系数c*0=0.01，波浪幅值A*=0.2）Fig.8 Change of potential energy in the direction of pitch freedom under various parameters(Damping coefficient c*0=0.01,wave amplitude A*=0.2)

2.4 规则波激励下铰接双浮体波能转换器的波能捕获特性

为了探究铰接双浮体波能转换器提升效率的效果和机理，本节将研究本装置在规则波下的波能捕获特性。为了与文献[33]中的经典双模块波能转换器进行对比研究，图9 给出了该文献中传统线性波能转换器的捕获宽度随波浪频率和阻尼系数变化云图。从图中可以看出，在无量纲波浪频率ω*=1.80 时，有一个能量捕获相对较大的频带，当阻尼系数c*0=0.01 时，该筏式波能捕获系统的捕获宽度达到最大。

图9 线性系统捕获宽度比随波浪激励频率和阻尼系数变化图（波浪幅值A*=0.2，弹簧刚度系数 k*0=0）Fig.9 Capture width ratio of linear system versus wave frequency and damping coefficient(Wave amplitude A*=0.2,spring stiffness k*0=0）

采用图8（b）中的非线性系统初始拉伸比和刚度系数参数，且采用线性系统获得的最优阻尼系数，计算非线性系统的捕获宽度比随入射波频率的变化曲线，并与线性系统最优捕获宽度比随入射波频率的变化曲线进行对比，如图10所示。从图看出，通过引入负刚度机构，可有效提高系统的捕获宽度比峰值，同时向低频拓宽能量捕获的频带。

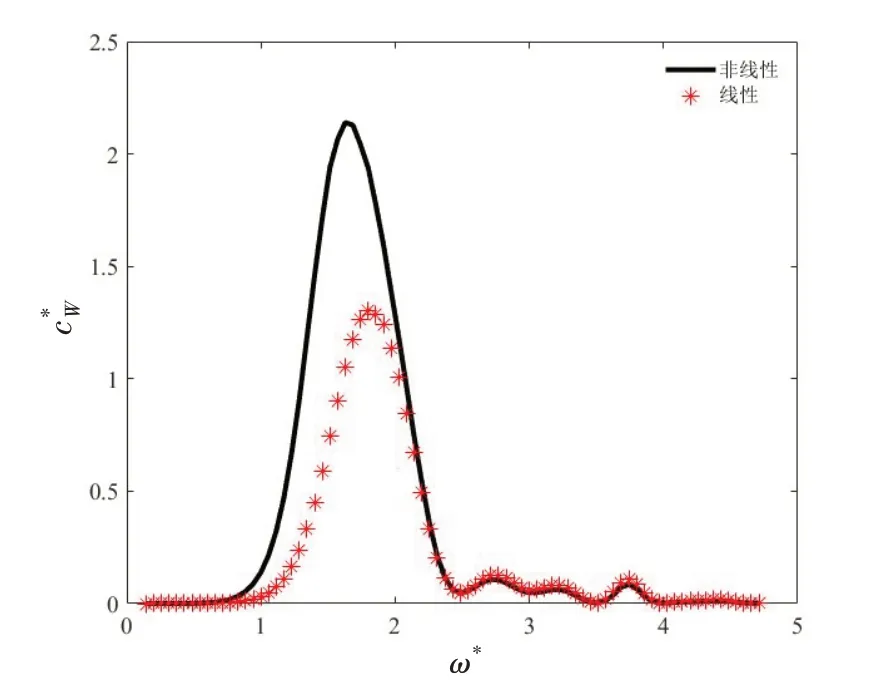
图10 捕获宽度比随波浪激励频率的变化图（阻尼系数c*0=0.01，波浪幅值A*=0.2，非线性系统弹簧参数为 k*0=4, α=0.7）Fig.10 Variation of capture width ratio with wave excitation frequency(Parameter damping coefficient c*0=0.01,wave amplitude A* = 0.2,the nonlinear system parameters of the spring k*0=4, α=0.7)

为了揭示引入非线性刚度机构提高波能捕获效率的机理，下面分析线性和非线性波能转换器的势能图和相轨迹图。

图11（a）和图11（b）分别是取图10 中线性系统和非线性系统捕获宽度比峰值处对应的波浪频率下（非线性系统ω*=1.56，线性系统ω*=1.80）纵摇自由度势能和相轨迹图。对比势能云图可知，通过引入非线性刚度机制，系统纵摇运动的势能曲面从图11（a）所示的圆形变为图11（b）所示的椭圆，且图11（b）中势能等值线的椭圆长半轴方向与两浮体纵摇运动的模态方向基本相同，由此可诱导浮体产生更大的纵摇运动。同时对比线性和非线性相轨迹图可知，由于非线性刚度机构的加入，椭圆形势能曲面会使得浮体纵摇运动轨迹由椭圆状变成近乎斜线状。由振动理论可知，即两个浮体的纵摇运动几乎变成反向运动，也可增大相对纵摇角度，从而可以提高波能捕获效率。

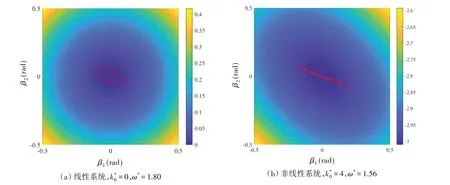
图11 线性系统与非线性系统势能曲面与相图（阻尼系数c*0=0.01，弹簧初始拉伸比α=0.7，波浪幅值A*=0.2）Fig.11 Contour diagram of potential energy and phase diagram of linear system and nonlinear system(Damping coefficient c*0=0.01,spring stretch ratio α=0.7,wave amplitude A*=0.2)

以上仅分析了某特定非线性刚度机构参数的波能捕获特性，附加装置的参数配比会直接影响系统的刚度特性进而影响系统的波能捕获特性。下面继续分析非线性机构参数配比对能量捕获特性的影响。为了评价不同参数的能量捕获性能，选择峰值捕获宽度比C*Wmax和相应的峰值频率（亦即中心频率）ω*max作为两个关键指标，探索非线性刚度机构的相对最优参数。图12（a）和图12（b）分别给出了不同刚度和初始弹簧拉伸比所对应的峰值捕获宽度比和相应的峰值频率云图，图中红色实线分别表示未施加非线性刚度机构的线性系统所对应的峰值捕获宽度比和峰值频率值。从图12（a）可以看出，红实线将参数域分成两个区域，当非线性系统参数处于左上角区域时，附加的非线性系统将起到负面作用，即降低系统的捕获宽度比，当系统参数处于右下角区域时，可有效提高系统的捕获宽度比。从图12（b）可以看出，红实线将参数区域分割成三个条带区域，但参数处于中间蓝色条带时，波能捕获频带会相应地向低频移动，有利于波能转换器捕获低频波浪能量。综合图12中的峰值捕获宽度比和峰值频率云图可知，应将非线性系统的参数设置在C点所在的黄色条带上，此时附加的非线性刚度机构一方面可有效提高系统的波能捕获宽度比，另一方面可以向低频拓宽波能捕获频带，从而捕获更多的低频波浪能量。从最大的峰值捕获宽度比来看，图12（a）中最优参数下的最大捕获宽度比（其值为2.14）比线性系统峰值（其值为1.30）提高65%。

图12 刚度和初始弹簧拉伸比所对应的最大捕获宽度比和相应的峰值频率（阻尼系数c*0=0.01，波浪幅值A*=0.2）Fig.12 Maximum capture width ratio and corresponding peak frequency corresponding to stiffness and initial spring tension ratio(Damping coefficient c*0=0.01,wave amplitude A*=0.2)

为了解释图12（a）和图12（b）中的现象，选取图12（a）中三个典型点参数，绘制系统的纵摇运动相轨迹和势能图，如图13 所示。A、B、C三个点对应的坐标值分别为α=0.5，k*0=18；α=0.72，k*0=10；α=0.86，k*0=6。

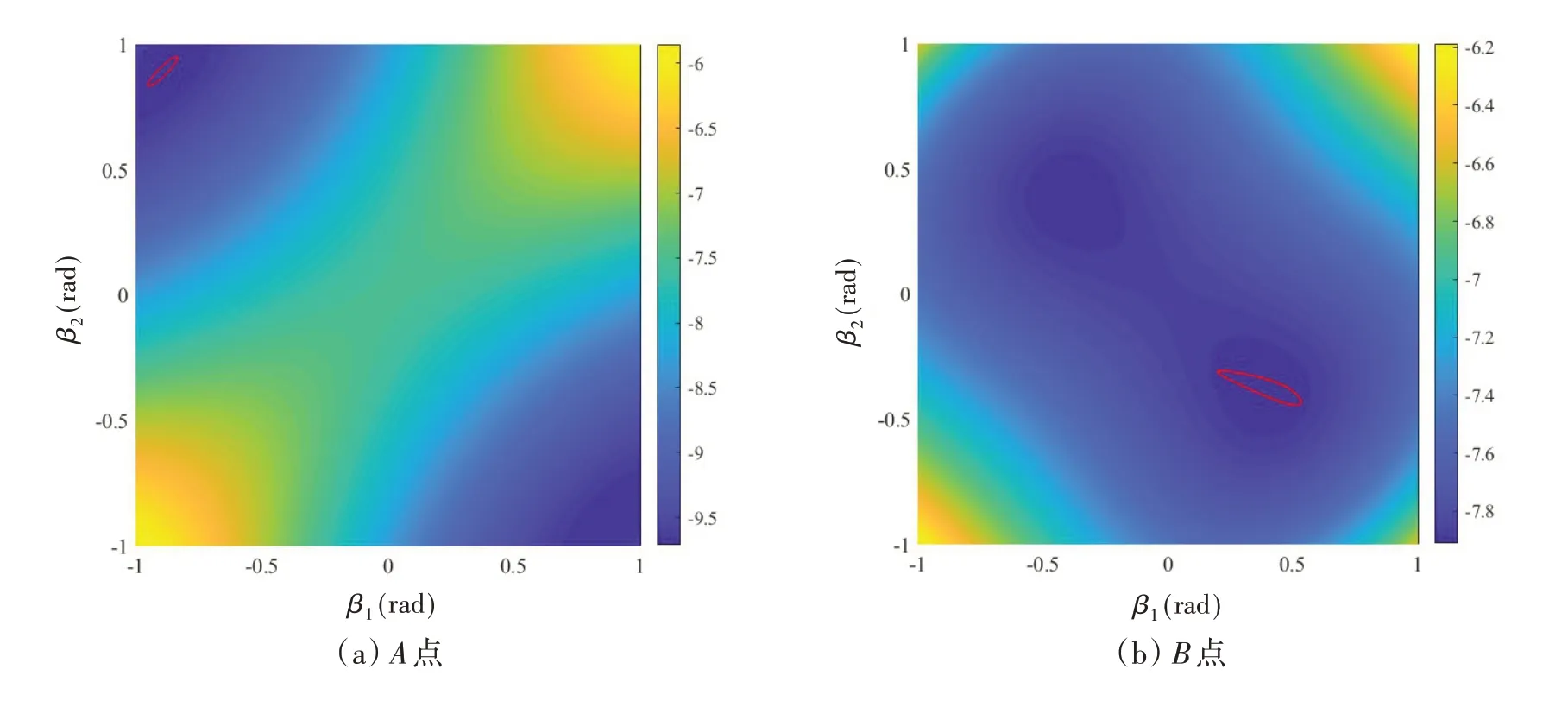
图13 典型参数下系统纵摇势能曲面与相轨迹图（阻尼系数c*0=0.01，波浪幅值A*=0.2）Fig.13 Pitching potential energy surface and phase trajectory of the system under typical parameters(Damping coefficient c*0=0.01,wave amplitude A*=0.2)

对于图12（a）深蓝色区域，从图13（a）可以看出，当附加负刚度取该参数时，系统呈现双井势能特性，两个井之间有一个相对较高的势垒，如同山脊一般。从图13（a）的轨迹可以看出，在A点，铰接浮体波能转换器由于双井势能的作用，使其始终处于井内的小幅运动，所以该参数下非线性刚度波能转换器的波能捕获宽度比很小。与图13（a）相比，图13（b）中的势垒急剧下降，两个势能井之间的距离也缩小了，浮体的运动可以越过较低的势垒，并且其相图轨迹接近椭圆。与图13（a）和图13（b）相比，图13（c）中的运动轨迹更平坦、更长。与图13（b）中的现象一样，轨迹越扁平，两个浮体的纵摇运动就更接近反相振荡，可以计算出其对应的纵摇响应相位差分别为0.41、2.62、2.77，即处于C点的两浮体纵摇运动响应更接近反向运动。因此，对于该铰接非线性波能捕获系统的捕获效率提升的机理是：通过引入负刚度机构，系统的弹性力在纵摇运动的相位平面上能形成一个椭圆势井，其长轴接近铰接浮体纵摇运动的模态方向，一方面放大模块的纵摇运动幅值，另一方面致使相对纵摇运动的相位差为反向，起到被动相位控制的作用。

由振动理论可知，不同于线性系统，非线性系统的响应与激励力幅值相关，所以下面进一步分析波高参数对波能捕获效率的影响。选取图13（c）中的弹簧参数，展示在不同波浪幅值下的非线性波能转换器的捕获宽度比随波浪频率和阻尼系数的变化云图，如图14所示。由图14（a）可知，黄色区域捕获宽度最大，通过比较图9 和图14（a），可以看到非线性波能转换器的峰值捕获宽度比是线性波能转换器的1.65 倍，非线性波能转换器的最佳阻尼系数也小于线性波能转换器。非线性波能转换器的频带宽度大于线性波能转换器的频带宽度。由图14 可知，在不同波振幅的影响下，非线性波能转换器的捕获宽度比取决于不同的入射波振幅，捕获宽度比随波振幅的增加而减小。这是由于引入负刚度机构后，系统呈现非线性刚度特性，即负刚度可减小浮体静水平衡位置处的刚度，但会提高系统在大幅运动时的刚度，从而会抑制大幅运动。

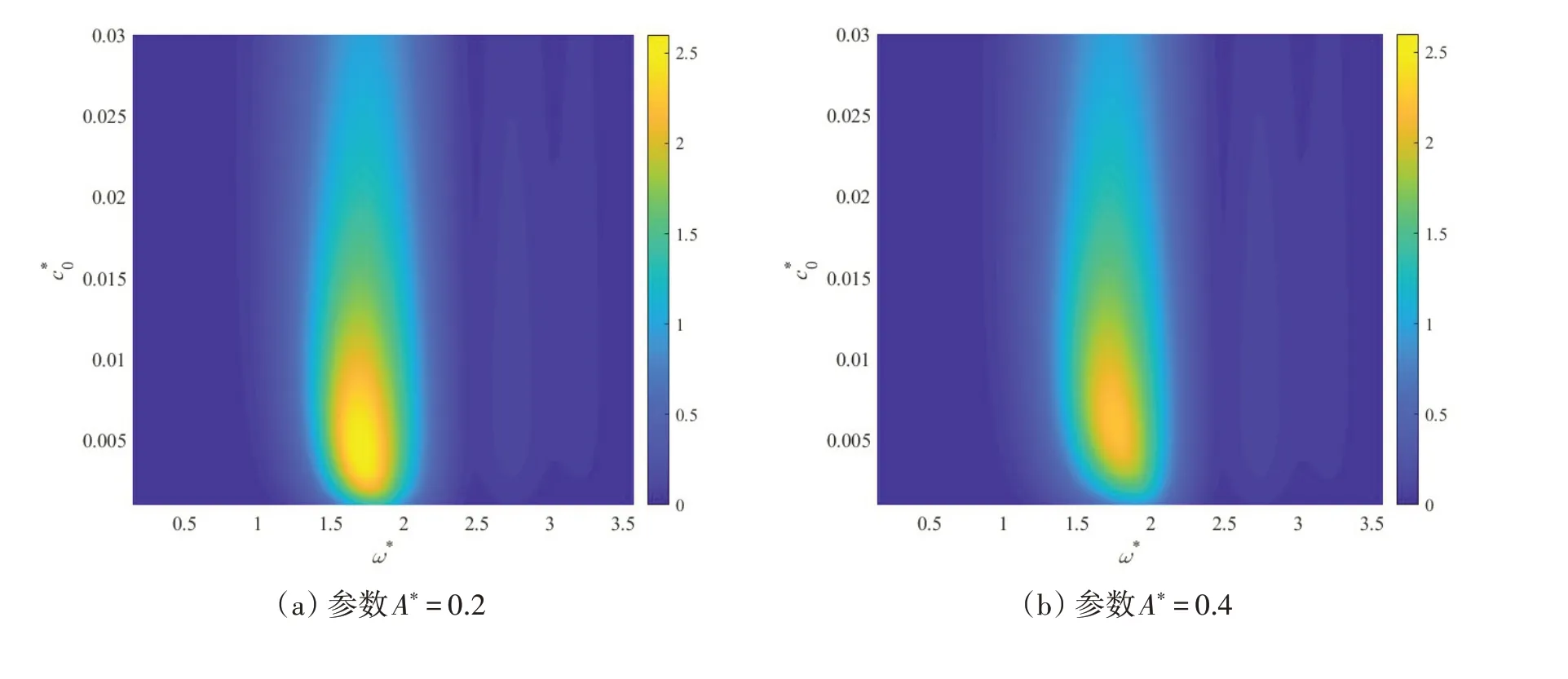
图14 非线性系统各参数下的捕获宽度（阻尼系数c*0=0.01，弹簧刚度系数k*0=6，弹簧初始拉伸比 α=0.86）Fig.14 Capture width of nonlinear system under various parameters(Damping coefficient c*0=0.01,spring stiffness k*0=6,spring stretch ratio α=0.86)

3 结 语

本文针对传统线性铰接双浮体波能转换器的波能捕获效率低的问题，提出了新型非线性刚度波能转换装置，研究了双浮体非线性波能转换器的能量捕获特性。首先，本文针对双浮体铰接波能转换器，提出了一种新颖的非线性刚度机构，相比于传统的非线性刚度机构，能够在保持功用性的前提下，结构更加简单，易于工程实现。其次，通过数值仿真分析，研究了铰接双浮体非线性刚度波能转换器的波能捕获效率，结果表明非线性刚度机构能通过设置适当参数，扩大能量吸收的频带，将谐振峰值移至低频区域，从而提高波能捕获效率。最后，揭示了非线性刚度机构提高双浮体铰接波能转换器的捕获效率的相位控制新机理，即系统的弹性力在纵摇运动的相位平面上能形成一个椭圆势井，其长轴接近铰接两浮体纵摇运动的模态方向，使两浮体的纵摇运动趋于反向，实现被动相位控制的作用，有利于波浪能量的捕获。同时需要说明的是，本文仅开展了数值仿真分析，该非线性波能捕获机制还需要开展试验研究进行验证。