非对称空间统计信道模型及其MIMO多天线系统

周 杰 曹志钢 菊池久和

(1 南京信息工程大学电子与信息工程学院，南京210044)

(2日本国立新泻大学电气电子工学科，新泻950-2181)

移动通信的本质是利用无线信道进行信息的有效传输，因此无线信道要成为一种可靠的高速通信媒质还存在着许多挑战.无线信道易受各种噪声、干扰和其他信道因素的影响，还由于用户的移动和信道的动态变化而使系统受到极大的不确定性，严重影响通信效率和质量，因此多年来无线信道的研究一直受到研究者的关注.建立能够准确描述信道多径效应的无线信道模型，也是分析MIMO多天线系统的重要基础［1-5］.

文献［6-7］提出了散射体空间分布圆模型(geometrically based single bounce model，GBSBM)和椭圆模型(ellipse based single bounce model，EBSBM).数据结果证明，GBSBM 模型能估计宏小区(macrocell)移动通信环境下重要的信道参数，EBSBM 模型能估计微小区(microcell)移动通信环境下重要的信道参数，但是GBSBM 和EBSBM 模型的估计结果不够准确.文献［8-14］提出了散射体高斯(Gaussian)分布圆模型(Gaussian scatter density model，GSDM)以及空心圆环模型(hollow-disc scatter density model，HSDM).Jiang 等［15-17］给出基于瑞利分布和指数分布圆模型(exponential scatter density model，ESDM).通过研究发现，以上所有模型都是散射体空间分布对称型分布模型，较符合蜂窝移动通信系统室外宏小区、微小区以及微微小区(picrocell).但对于系统中指向性天线的设计和使用使得信号覆盖区域呈现非对称特点，对不同的室内环境，如不规则形状以及介电性质差别很大的开放性工厂、办公室、金工车间和走廊等，都可能使信道环境呈现散射体的非均匀分布和分布环境的非对称性.

本文针对在非均匀散射体分布以及非对称空间分布的移动通信环境，引入几何分割法导出基于散射体高斯分布的非对称空间统计信道模型.与以上提出的模型相比，本模型更加符合实际的移动通信环境，对于研究非对称和非均匀散射体分布空间提供了有利的研究工具.

1 非对称空间统计信道模型

1.1 非对称信道模型和散射体非均匀分布函数

如图1所示，信道模型中移动台(mobile station，MS)和基站(base station，BS)之间距离为D，且所有散射体分布在以BS 为覆盖小区的圆形散射区域R 内，指向性天线使得散射区域形成了非对称型的信道模型.如果单独看此非对称型信道模型，则形成以图1所示的以直达视距(line of sight，LOS)为坐标的非对称型信道环境.假设坐标圆点在基站BS 处，则移动台MS 坐标即为(D，0)，最小绝对时延参数为τmin=τ0=D/c，其中，c 为光速.

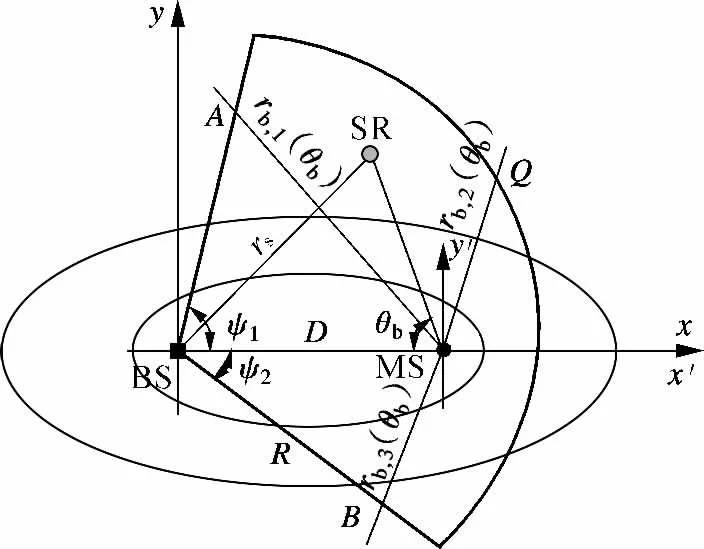
图1 非对称信道空间模型

与文献［11，17］相同，本模型假设BS 附近的散射体非均匀分布服从高斯分布，其极坐标的分布密度函数为

式中，NG为分布密度函数的归一化常数;rs为基站到散射体的距离;φ 为基站信号发出的角度;σG为高斯参数;R 为散射体区域半径;ψ1和ψ2分别为散射体区域上、下主瓣角.

1.2 AOA/TOA 联合概率和边缘概率分布

直接从极坐标(rs，φ)转换成(rb，θb)比较困难，但是可以通过从直角坐标(x，y)转换成(x′，y′)来求出极坐标(rb，θb)下的联合概率密度函数［18－19］，即

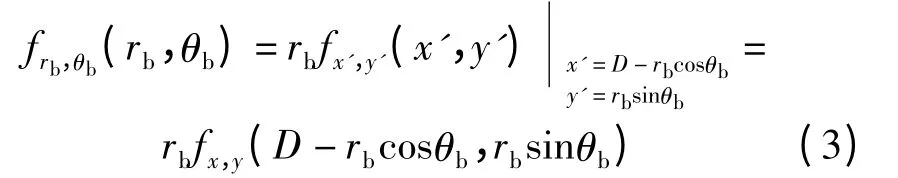
利用以上坐标变化，可简单推导出波达信号到达角度(angle of arrival，AOA)、到达时间(time of arrival，TOA)的概率分布为［6］

式中，入射角θb满足0≤θb≤2π;时延参数满足从图1信道空间模型可得ρ1和ρ2表达式为

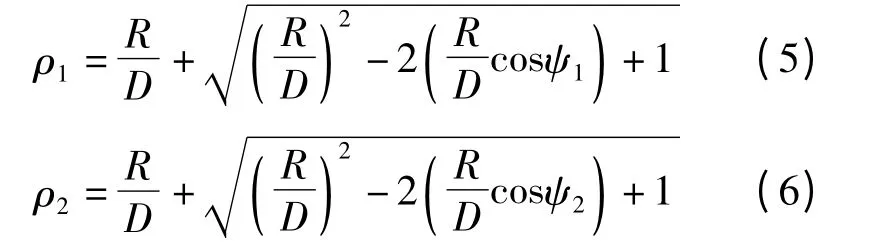
为求解AOA 的边缘概率分布，式(4)可以直接对时延τ 进行积分，另外也可直接使用散射体非均匀分布函数进行坐标变换，再积分得到其概率分布.由非对称信道空间模型图1可知，在参数0≤θb≤2π 范围内，AOA 的概率分布函数f(θb)可分为3种情况.

如图1所示，将基站MS 与散射点SP 的连线延伸，与边界圆扇形上边界半径直线相交于A 点，令rb，1(θb)为MS 与A 点的距离，则

在式(7)中代入散射体分布函数式(3)、(8)，即可求得数值解AOA 的概率分布函数.

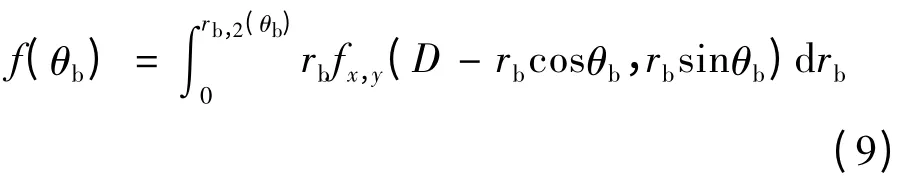
将基站MS 与散射点SP 的连线延伸，与rs=R的边界圆相交于Q 点，令rb，2(θb)为MS 与Q 点的距离，则

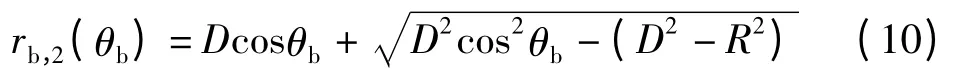
将基站MS 与散射点SP 的连线延伸，与边界圆扇形下边界半径直线相交于B 点，令rb，3(θb)为MS 与Q 点的距离，则

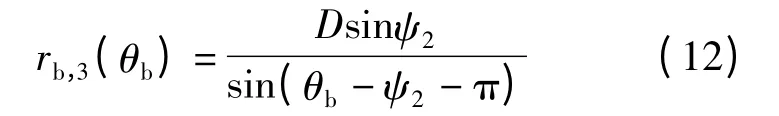
图1揭示了BS 和MS 之间具有相同路径时延τ 的散射体分布在同一个椭圆上，其焦点就落在BS 和MS 位置.为求解非对称信道模型中MS 的信号到达时间(TOA)的概率密度函数，可采用分段求解信号TOA 累积概率分布函数(cumulative distribution functions，CDFs)，即求解散射体落在椭圆内的概率与整体散射区域的概率比.由图1可知，在参数范围内，其波达信号TOA 的概率密度函数可以分为4 种情况.

在非对称空间信道模型以及非均匀散射体分布函数下，等传输时延τ 的椭圆区域与散射区域部分相交且落在扇形区域内时其累积概率分布函数为

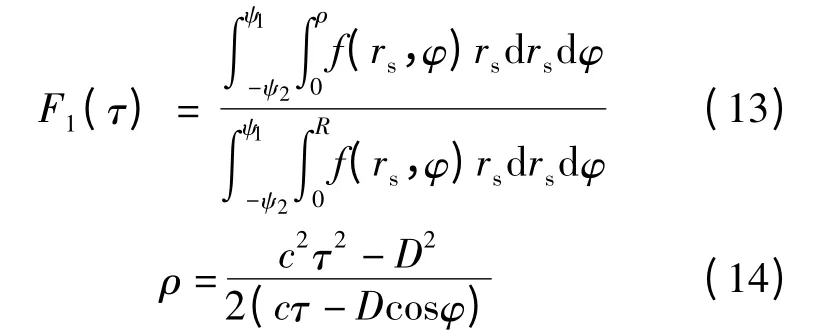
F1(τ)对自变量τ 求导微分可得MS 的波达信号的TOA 概率密度函数为

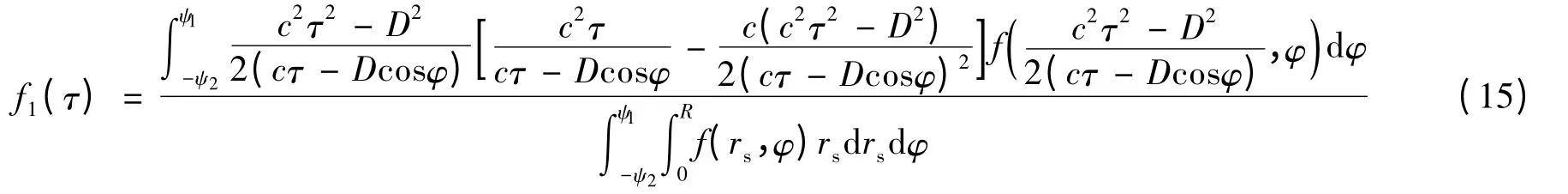
为简易表达复杂积分式，本文定义中间积分函数F(τ，φ)为

如图1所示，在等传输时延τ 的椭圆区域与散射区域上下半部分都相交，其累积概率分布函数为

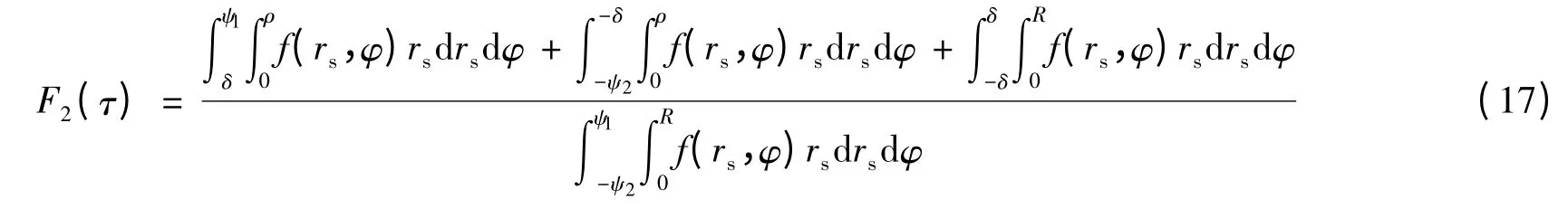
F2(τ)对自变量求导微分可得MS 的波达信号的TOA 概率密度函数为

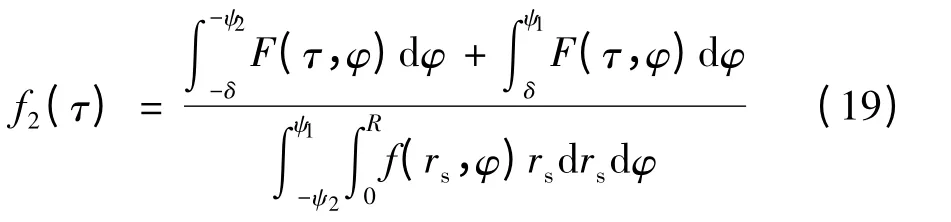
式中，F(τ，φ)中间函数由式(16)给出.

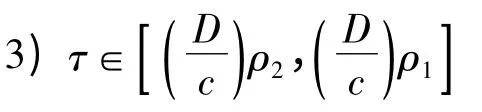
如图1所示，在等传输时延τ 的椭圆区域与散射区域上半部分相交，下半部分在其椭圆内，其累积概率分布函数为

F3(τ)对自变量τ 求导微分可得MS 的波达信号的TOA 概率密度函数为

式中，F(τ，φ)中间函数由式(16)给出.

在等传输时延τ 的椭圆区域与散射区域全相交且包含整体散射区域时，由于不存在散射体，故MS 的波达信号的TOA 概率密度函数为

2 MIMO 多天线阵列系统

如图2所示，线性阵列(ULA)具有结构简单，圆形阵列(UCA)具有全方向性特性，在移动通信领域应用得较多.如果MS 端MIMO 阵列为ULA时，入射信号空间导向矢量为

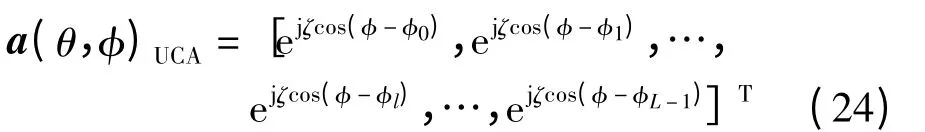
图2 四单元MIMO ULA 和UCA 阵列模型

对于图2所示空间结构的MIMO 阵列天线，则阵元m 和n 之间的空间衰落相关函数(spatial fading correlation function，SFCF)可表示为［1－4］

式中，E［·］为数学期望;上标(·)*表示共轭复数;~hm为阵元m 接收信号能量均值;am(θ，φ)和an(θ，φ)分别为阵元m 和n 的导向矢量;p(θ，φ)为波达信号AOA 的三维空间分布概率函数.如果仅考虑方位角平面，此函数即为式(7)、(9)和式(11).

在移动通信系统性能分析中，信道容量能够全面表征MIMO 系统的性能.发送端在无法获知信道信息时，最优的策略是将功率平均分配到各天线阵元上，此时信道的平均容量为

式中，INr为Nr维单位矩阵;MIMO 信道矩阵H 可以表示为其中，Rr为接收端的阵元间相关矩阵，Rt为发射端阵元间相关矩阵，由于不考虑发送端的相关性，因此Rt为单位矩阵，Hw为同分布的复高斯随机矩阵;P/σ2为信道信噪比;Nt为发射端天线数量;Nr为接收端天线数.

3 数值结果与分析

通过数值计算和仿真，给出由于指向性天线或者特殊室内环境所造成的非对称空间参数、MIMO分布式天线结构以及散射体分布等因素对MIMO信道特征和接收性能的影响.为不失一般性，本文定量地给出非对称扇形微小区模型参数为R =100 m 和D=50 m，基站BS 配置智能指向性天线主瓣宽度α=120°和移动台MS 的位置参数ψ1=80°和ψ2=40°.MS 接收端配置多天线MIMO(见图2)阵列设计为四单元MIMO ULA 线性阵列和UCA 圆环阵列，入射信号信噪比为20 dB.

在散射体高斯分布条件下，非对称空间统计信道的AOA/TOA 联合概率密度如图3所示.从图中可以发现，移动台MS 接收信号基本上是在小角度(θb=0°)或者主要在最小时延处，而在大角度(θb=180°)和最长时延处，其概率密度较小.且由于分布空间结构的非对称性，使得AOA/TOA 概率分布图呈现两片区域，且左右处于非对称状态.另外图3中显示，联合概率函数值在(τp，± θp)点达到峰值，其中和θp=0+.

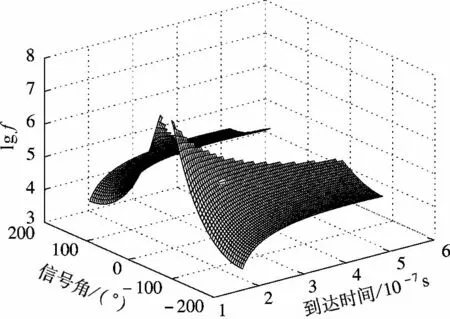
图3 散射体高斯分布AOA/TOA 联合概率分布

图4为高斯分布参数σG对AOA 概率密度的影响.由图可以得到，波达信号AOA 概率分布呈现左右非对称性特征，均仅有指数分布变化规律.其分布函数在空间模型中，ρ1和ρ2的θb点值上具有非连续性特征.图中还显示，在高斯分布模型中当σG变大时，其概率密度相对较小.如果移动台MS处于不同位置，在ψ1变大时相同到达角度(θb=50°)的概率密度变大.ψ1变大时散射体区域的上半部区域变大，故信号的反射和折射概率也变大.

图5为在散射体高斯分布下移动台MS 的TOA 边缘概率密度.当传输时延τ 超过ρ2}时，椭圆区域超过了散射体区域，TOA 的概率密度为零.图5表明，分布参数σG对TOA 概率密度的影响较大.当σG变大时，TOA 概率密度相对降低，TOA 还呈现非连续性断点，断点位于TOA 概率密度函数的第2 和第3 种情况的变化点上.因为几何信道模型呈现非对称形状，表明TOA 的概率分布趋势呈现不同特征，符合非对称信道特征的预期.

图4 高斯散射体分布参数σG 对波达信号角度AOA 概率分布影响

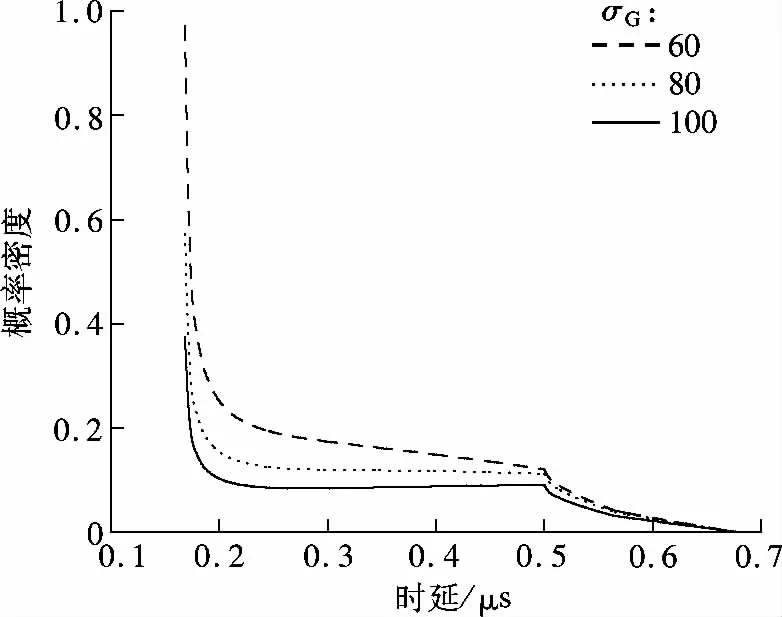
图5 高斯散射体分布参数σG 对TOA 概率分布影响

本文以非对称空间统计信道为基础，利用实际导出的移动台MS 的波达信号角度分布(见图4)数值解，考虑四单元多天线MIMO ULA 线性和MIMO UCA 圆环阵列的数值计算和分析阵元间的相关性.图6是散射体高斯分布下，ULA 阵列单元(1，2)的空间相关性系数.结果显示，空间相关性随着d/λ 的增大而减小.在分布参数σG较小时，由于散射体的分布较为均衡，使得空间相关性较为平滑，逐渐减小并趋近于0 值.在分布参数σG较大时，散射体的分布函数梯度较大，波达信号角度分布在较窄范围内，使得空间相关性呈现振荡下降，并趋近于0 值.

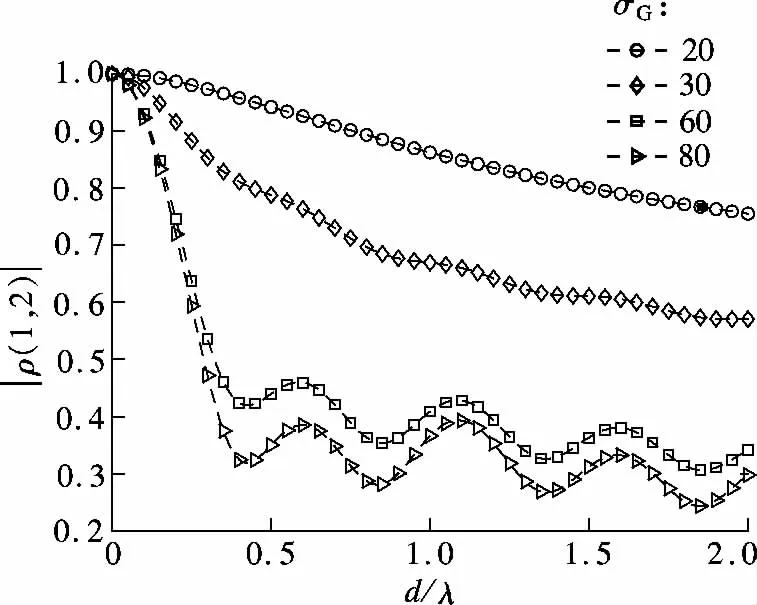
图6 多天线MIMO ULA 阵列单元(1，2)的空间相关性系数

图7 多天线MIMO 信道容量

本文考虑移动台MIMO 四单元ULA 和UCA的阵列配置(见图2)，分析和模拟仿真其接收信道容量.图7为高斯分布参数σG对ULA 和UCA 天线阵列信道容量的影响.图中显示，在两阵元间距d 和r 较小时，阵元相关性较大，信道容量较小.在天线阵列单元间隔d 和圆环半径r 从0 变到0.5λ 时，阵元间相关性系数快速降低，使其信道容量快速变大，在天线阵列单元间隔大于0.5λ 后，信道容量值逐渐趋于极限值方向，以小幅振荡平稳增长.在σG=20，d =0.25λ，ULA 天线阵列结构总长度为λ 时，此四单元MIMO ULA 信道容量为9 bits/(s·Hz).在σG=20，r =0.5λ 时，四单元MIMO UCA 信道容量为11.5 bits/(s·Hz)，与ULA信道容量相比，增长了27.7%，因此MIMO UCA 具有明显的优越性.如图2所示，在d =0.25λ 和r =0.5λ，UCA 和ULA 阵列具有相同的结构长度，但UCA 以占据更大的空间面积为代价，提高了任意两阵元间的间距，减小了相关性系数，从而获取更高的信道容量.

4 结语

针对由于智能指向性天线或室内特殊环境造成非对称空间多径衰落信道，本文研究了非对称空间统计信道模型.在散射体分布服从高斯分布和指数分布情况下，导出波达信号AOA 和TOA 的概率密度函数，揭示了此模型下移动台MS 端的各信道参数变化特征.应用此统计信道模型，研究和分析了多天线MIMO ULA 线性阵和UCA 圆环阵元间信道空间衰落相关性，分析得到其分集接收容量，比较了ULA 和UCA 阵列的优越性.分析结果显示，本模型的信道参数估计符合实际的移动通信环境，拓展了空间统计信道模型的应用研究，为评估多天线MIMO 系统空时处理算法和仿真无线系统提供有力的工具.

References)

［1］Intarapanich A，Kafle P L，Davies R J，et al.Geometrically based broadband MIMO model with tap-gain correlation［J］.IEEE Trans Veh Technol，2007，56(6):3631-3641.

［2］Tsalolihin E，Bilik I，Blaunstein N.MIMO capacity in space and time domain for various urban environments［C］//Proceedings of the 5th European Conference on Antennas and Propagation.Rome，Italy，2011:2192-2196.

［3］Ivanis Predrag N.Closed-form level crossing rates expressions of orthogonalized correlated MIMO channels［J］.IEEE Trans Veh Technol，2011，60(4):1910-1916.

［4］Buyukcorak S，Karabulut Kurt G.Simulation and measurement of spatial correlation in MIMO systems with ray tracing［C］//5th International Conference on Signal Processing and Communication Systems.Honolulu，HI，USA，2011:1-5.

［5］Jakes W.Microwave mobile communications［M］.New York:IEEE Press，1974:1-10.

［6］Ertel R B，Reed J H.Angle and time of arrival statistics for circular and elliptical scattering model［J］.IEEE J Sel Areas Commun，1999，17(11):1829-1840.

［7］Petrus P，Reed J H，Rappaport T S.Geometrical-based statistical macrocell channel model for mobile environment［J］.IEEE Trans Commun，2002，50(3):495-502.

［8］Olenko A Y，Wong K T，Abdulla M.Analytically derived TOA-DOA distributions of uplink/downlink wireless cellular multi-paths arisen from scatteress with an inverted-parabolic spatial distribution around the mobile［J］.IEEE Signal Proc Let，2005，12(7):516-519.

［9］Olenko A Y，Wong K T，Ng E H.Analytically derived TOA-DOA statistics of uplink/downlink wireless multipaths arisen from sactterers on an hollow-disc around the mobile［J］.IEEE Antenn Wirel Pr Lett，2003，2(1):345-348.

［10］Jaafar I，Boujemaa H，Siala M.Angle and time of arrival statistics for hollow-disc and elliptical scattering models［C］//Proc of International Conference on Signals，Circuits and Systems.Nabeul，Tunisia，2008:1-4.

［11］Janaswamy R.Angle and time of arrival statistics for the Gaussian scatter density model［J］.IEEE Trans Wirel Commun，2002，1(3):488-497.

［12］Wu Y I，Wong K T.A geometrical model for the TOA distribution of uplink/downlink multi-paths assuming scatterers with a conical spatial density［J］.IEEE Antenn Propag M，2008，50(6):196-205.

［13］Kong S H.TOA and AOD statistics for down link Gaussian scatterer distribution model［J］.IEEE Trans Wirel Commun，2009，8(5):2609-2617.

［14］Khan N M，Simsim M T，Ramer R.Modeling spatial aspects of mobile channel for macrocells using Gaussian scattering distribution［C］//The 3rd International Symposium on Wireless Communication Systems.Valencia，Spain，2006:616-620.

［15］Jiang L，Tan S Y.Simple geometrical-based AOA model for mobile communication systems［J］.Electron Lett，2004，40(19):1203-1205.

［16］Jiang L，Tan S Y.Geometrically based power azimuth spectrum models for mobile communication systems［J］.Microwave and Optical Technology Letters，2007，49(9):2093-2097.

［17］Jiang L，Tan S Y.Geometrically based statistical channel models for outdoor and indoor propagation environments［J］.IEEE Trans Veh Technol，2007，56(6):3587-3593.

［18］Baltzis K B，Sahalos J N.A simple 3D geometric channel model for macrocell mobile communication［J］.Wireless Pers Commun，2009，51(2):329-347.

［19］Baltzis K B.On the geometric modeling of the uplink channel in a cellular system［J］.Journal of Engineering Science and Technology Review，2008，1(1):75-82.

［20］Foschini G J，Gans M J.On limits of wireless communications in a fading environment when using multiple antennas［J］.Wireless Pers Commun，1998，6(3):311-319.