基于自由液面预测的非线性液体晃动问题的数值模拟

张海涛 孙蓓蓓 陈建栋

(东南大学机械工程学院，南京211189)

充液容器在运动过程中产生的液体晃动是一种较为复杂的流体运动现象，具有较强的非线性.液体晃动及其动力学特性涉及到诸多工业领域，因此对于液体晃动的研究显得尤为重要［1］.在共振情况下，晃动产生的冲击载荷将会严重地影响充液容器的结构完整性及其运动稳定性，所以在储液罐及其附属系统的设计过程中，一定要考虑到液体晃动的固有频率，以避免共振的发生.

早期关于液体晃动的研究主要是基于不可压缩流体的势流模型，运用解析或者半解析的方法，计算和分析贮液箱微幅线性晃动和小幅弱非线性晃动［2-3］.从20 世纪80年代开始，非线性晃动逐渐成为研究的热点，而且随着计算机技术的发展，数值方法成为液体晃动研究的主要方法.岳宝增［4］研究了俯仰激励下的液体大幅晃动问题，采用ALE方法求解N-S 方程，并采用Galerkin 加权余量法推导有限元数值离散方程.Celebi 等［5］研究了部分充液容器中黏性流体的非线性晃动，采用有限差分方法求解N-S 方程，并采用VOF 方法追踪自由液面.另外，还有一些学者采用其他有限差分［6］、有限元［7-8］、边界元［9-10］等数值方法研究液体晃动问题.

自由液面是晃动方程中的一条边界，而自由液面本身又是未知的运动函数，故而成为晃动研究中的一个难点.在数值模拟过程中，一般都要采用特殊的方法处理自由液面，如MAC 法、VOF 法、levelset 法等.Frandsen 等［11-12］采用σ 变换方法来处理自由液面的问题，将不规则的求解区域变换为规则的矩形区域，且在计算过程中不需因自由液面的改变而重划网格，也不需要对自由液面进行光滑化，体现出一定的优越性.本文提出了一种新方法来处理σ 变换之后的非线性晃动方程，并采用有限差分方法进行离散求解.其主要思想是在每一个时间步长的迭代过程中，先预测出下一时间层上的自由液面形状，并且对非线性项进行近似处理，从而将非线性方程组转化为线性方程组.通过该数值方法，本文计算和研究了二维矩形贮液箱内的非线性晃动问题.

1 数学模型

假设液体是无旋、无黏、不可压缩的理想流体，且在晃动过程中不出现液体的翻转或者破碎现象.采用势流模型进行描述，并忽略表面张力的影响.矩形充液容器是刚性的，长为b，静止时水深为h，如图1所示.建立绝对坐标系XOZ，并假设容器在该坐标系下有水平运动X(t).同时建立一个固连于充液容器的相对坐标系xoz，坐标原点设定为左壁面和未扰动水平液面的交点，向右和向上为正方向.在相对坐标系下考虑液体晃动，得到如下方程组:

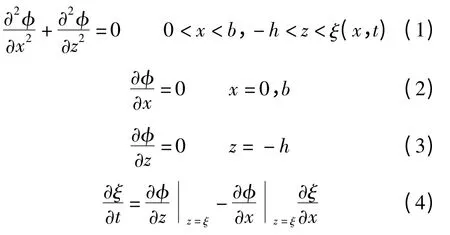
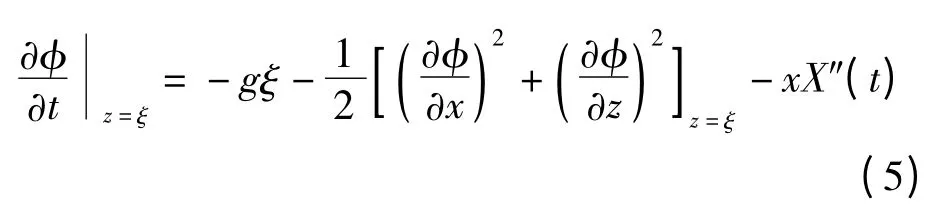
式中，φ 表示速度势;ξ(x，t)为波高函数，表示t 时刻、位置为x 处的自由液面流体质点偏离未扰水平自由液面的距离;g 表示重力加速度.式(1)为理想流体的连续性方程，式(2)、(3)为固壁边界条件，式(4)、(5)分别为自由液面的运动学条件和动力学条件.

图1 晃动模型图

2 数值算法

首先采用σ 变换方法进行处理.σ 方法本质上是一种坐标变换，可以将带有自由液面的复杂流体域转化为规则区域.定义如下新自变量σ 和新函数Φ:

于是式(1)～(5)变化为

原来的流体区域中，自变量z 满足－ h ＜z ＜ξ(x，t).变换之后，新自变量σ 满足0 ＜σ ＜1，而自变量x 在变换前后不发生变化，故流体域就转化为矩形区域.

对上述方程采用有限差分方法进行离散，在每一个时间步长内迭代求解.假设第k 层上的各参数都是已知的，设法求解第k+1 层的各参数.针对晃动中出现的自由液面和非线性边界条件这2 个较难处理的问题，本文分别采用预测－校正方法和近似代替方法来解决.

对于式(7)～(9)，在第k +1 层上进行离散.式(7)和(8)中，ξk+1和Φk+1是相互耦合的未知数，难以直接求解，若能减少未知数的数目，则会大大简化求解过程.事实上，第k +1 层的式(7)是由下式经σ 变换得到:

如果采用式(10)的显式格式估计出ξk+1的预测值，并代入到式(12)中，那么式(12)的4 条边界就完全确定了，相当于式(12)或式(7)成为了仅与内部区域Φk+1有关的方程.对于第k +1 层的式(8)作相同处理，代入ξk+1的预测值，使之仅以Φk+1作为未知数，而第k +1 层的式(9)不含有ξk+1，故不需要作类似处理.

对关于σ =1 的2 个边界条件，即式(10)和(11)在第层上进行离散.这里将ξk+1和Φk+1均视为未知数.可看出和是 明 显的非线性项，数值计算时应代入的值.然而，本身也是未知的，故本算法仅代入Φk和ξk的值作为的近似.而对于式中的线性部分则采用Crank-Nicolson 格式进行处理，以得到关于ξk+1和Φk+1(σ =1)的隐式方程.另外，对于式中其他ξ 作为分母以及Φ 和ξ偏导相乘的情况，也可采用类似的处理方式.于是式(10)和(11)可离散成

对时域离散后的方程再进行空间域上的有限差分离散，即可得到线性方程组，同时隐格式保证算法具有良好的稳定性.最后，解出的ξk+1将作为第k+1 层波高函数ξ(x，t)的校正值.

3 数值结果与讨论

下面计算几种晃动的情况来验证数值方法的准确性.建立一个二维充液容器的模型，设定容器的长度和水深分别为b=2 m，h =1 m.液体晃动的固有频率为［3］

3.1 自由晃动

此情况下，容器本身静止不动，相对坐标系xoz与绝对坐标系重合.设初始时刻液体是静止的，仅存在一个初始余弦型自由液面，即

图2 不同网格、时间步长下的左壁处自由液面质点振动比较

第1 个算例设定ah=0.2 m，n =1，对应于第一阶非线性驻波的情形，以该算例来验证数值算法的收敛性.图2显示了运用该数值方法算出的左壁处自由液面质点振动的时间历程，其中图2(a)显示了采用不同空间网格的2 种结果的比较(时间步长都为5 ms)，图2(b)显示了采用不同时间步长的2种结果的比较(空间网格都为40 ×40).这里坐标轴运用外激励振幅和第一阶晃动固有频率进行了无量纲化，即

由图2可看出，采用不同的空间网格或者不同的时间步长，计算结果都是接近的，该数值算法具有一定的收敛性.

除收敛性外，算法的精度也同样需要验证.将数值解与解析近似解进行对比，其中解析近似解可根据非线性小参数展开法来获得［11］.图3(a)显示了2 种算法得到的左壁处自由液面质点振动的时间历程.通过比较可看出，数值解和解析解基本一致.此外，该图也反映出非线性晃动的一些特点:振动的时间历程并非正弦曲线;波峰与波谷的振幅不同，波峰的最大振幅大于波谷的最大振幅.图3(b)为数值解计算出的约半个周期内的自由液面运动图(从无量纲时间31.8 到34.6)，它说明非线性驻波中不存在驻点.

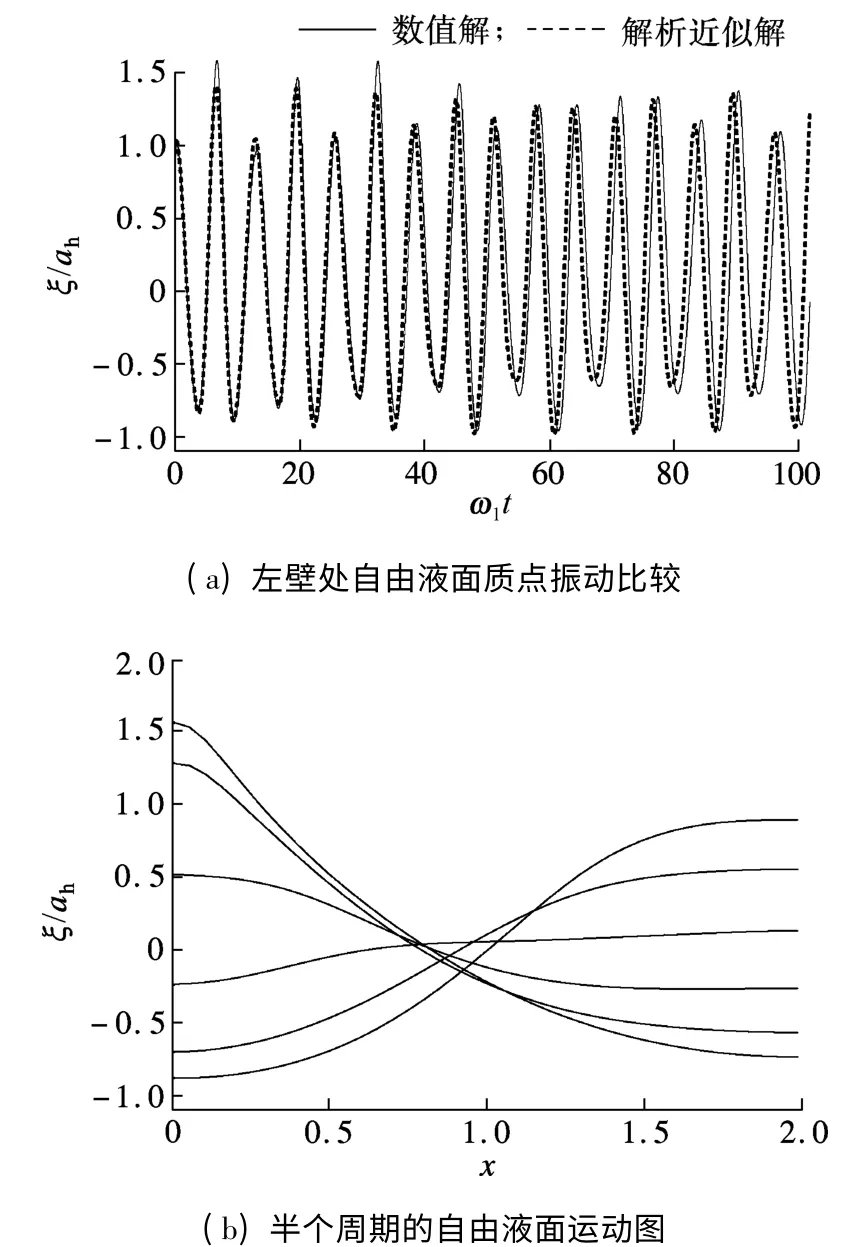
图3 第一阶非线性驻波

本文还计算了第三阶非线性驻波的情形.在初始自由液面中设定ah=60 mm，n =3.图4给出了第三阶驻波的计算结果.由图可看出，数值解和解析近似解仍是接近的，高阶驻波表现出的非线性特征与第一阶驻波较为类似.第二阶、第四阶等其他阶数的驻波情形也可以运用该方法进行计算.线性晃动理论认为，容器的横向受迫运动只能激励出液体晃动奇数阶的模态(如果考虑非线性因素，那么偶数阶模态对受迫晃动也有微小的影响［11］).另外，高阶晃动模态对晃动力的影响比较小.因此，液体晃动的第一阶模态和第三阶模态最为重要.

图4 第三阶非线性驻波

3.2 受迫晃动

设定容器作水平方向的简谐振动，其位移函数为X(t)=acos(ωt).并且设初始时刻液体是静止的，自由液面也是水平未扰动的.因此在相对坐标系中，初始条件应描述为

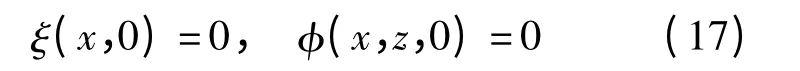
对于受迫晃动，同样可运用小参数法求解析近似解［11］，其解法与前述自由晃动的解析近似方法类似.计算几个算例并与解析解进行比较:①a =30 mm，ω=1.4ω1;②a=10 mm，ω=1.1ω1;③a=7 mm，ω=1.000 7ω1.这里ω1表示液体晃动的第一阶固有频率，②和③分别对应于晃动的一阶拍和一阶共振.在数值模型中取时间步长为6 ms，空间区域划分为40 ×40 的网格.图5为左壁处自由液面流体质点振动时间历程图.同样地，图5坐标轴也进行了无量纲化.

图5 受迫晃动左壁处自由液面质点振动图

从图5中可看出，数值解和解析近似解符合程度较好，说明该算法对于受迫晃动的数值模拟也是较为准确的.数值解和解析解均体现出非线性受迫晃动的特点，即波谷的幅值小于波峰的幅值.

3.3 行波

如果容器内液体的填充比例很低，那么接近于一阶晃动固有频率的外激励频率将会形成行波［8］.重新建立一个二维充液容器的模型，设定容器长度和静水深度分别为b =2 m，h =0.25 m.容器的位移函数中，设定a =10 mm，ω =0.999 8ω1.取时间步长为6 ms，由于这是一个浅水区域，故将空间划分为80 ×20 的网格，代入到数值模型中进行计算.图6为左壁处自由液面流体质点振动时间历程图，该图体现出更加明显的非线性效应:波峰的幅值非常高，而波谷的幅值则较为平均.图7(a)、(b)分别为无量纲时间40.7～43.1 和43.7～45.5 区段上的自由液面运动图，可看出，行波先是以较为平缓的幅度向左运动，当波峰接触到左壁时，就会迅速提升，大约在43.1 时刻达到最大值;当波峰下降之后，行波又会以平缓的幅度向右运动，如此往复.

图6 左壁处自由液面质点振动图

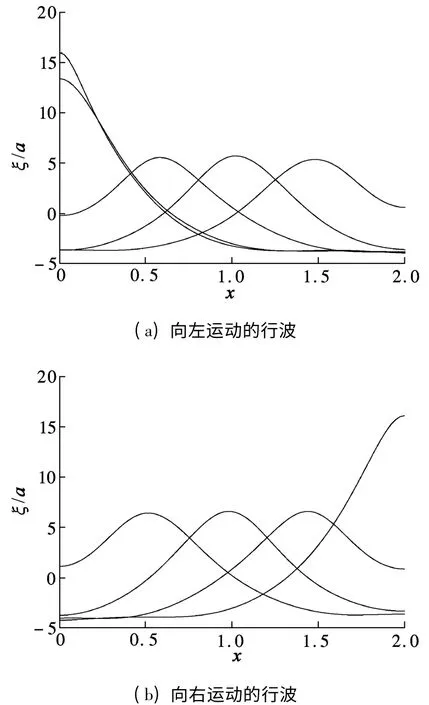
图7 行波的自由液面运动图

4 结语

本文采用一种数值方法计算了二维矩形容器内的液体晃动问题.先使用σ 变换将流体区域转化为矩形域，然后对变换后的方程运用预测校正和非线性近似技术，使之转化为线性方程，并使用有限差分方法离散求解.该数值算法较为简单，易于编程实现.通过对计算结果的比较，可看出算法精度较高，能够反映出非线性晃动的特点，亦可用来计算其他的液体晃动问题.而这种动边界上的预测校正格式则可用于求解含有运动边界的偏微分方程组.

References)

［1］岳宝增，祝乐梅，于丹.储液罐动力学与控制研究进展［J］.力学进展，2011，41(1):79-92.

Yue Baozeng，Zhu Lemei，Yu Dan.Recent advances in liquid-filled tank dynamics and control［J］.Advances in Mechanics，2011，41(1):79-92.(in Chinese)

［2］Abramson H N.SP-106 The dynamic behavior of liquids in moving containers ［R］.Washington DC:National Aeronautics and Space Administration，1966.

［3］Faltisen O M.A nonlinear theory of sloshing in rectangular tanks［J］.Journal of Ship Research，1974，18(4):224-241.

［4］岳宝增.俯仰激励下三维液体大幅度晃动问题研究［J］.力学学报，2005，37(2):199-203.

Yue Baozeng.Three dimensional large amplitude liquid sloshing under pitching excitation ［J］.Acta Mechanica Sinica，2005，37(2):199-203.(in Chinese)

［5］Celebi M S，Akyildiz H.Nonlinear modeling of liquid sloshing in a moving rectangular tank［J］.Ocean Engineering，2002，29(12):1527-1553.

［6］罗志强，陈志敏.基于Euler 方程有限差分方法驻波晃动模拟［J］.应用数学和力学，2011，32(11):1378-1390.

Luo Zhiqiang，Chen Zhimin.Sloshing simulation of standing wave with a time-independent finite difference method for Euler equations［J］.Applied Mathematics and Mechanics，2011，32(11):1378-1390.(in Chinese)

［7］闫锦，于洪亮，宋玉超.矩形液箱内液体晃动分析计算［J］.大连海事大学学报，2013，39(1):74-77.

Yan Jin，Yu Hongliang，Song Yuchao.Analysis of liquid sloshing in rectangular tank［J］.Journal of Dalian Maritime University，2013，39(1):74-77.(in Chinese)

［8］Wu G X，Ma Q W，Taylor R E.Numerical simulation of sloshing waves in a 3D tank based on a finite element method［J］.Applied Ocean Research，1998，20(6):337-355.

［9］Ansari M R，Firouz-Abadi R D，Ghasemi M.Two phase modal analysis of nonlinear sloshing in a rectangular container ［J］.Ocean Engineering，2011，38(11/12):1277-1282.

［10］Firouz-Abadi R D，Ghasemi M，Haddadpour H.A modal approach to second-order analysis of sloshing using boundary element method ［J］.Ocean Engineering，2011，38(1):11-21.

［11］Frandsen J B.Sloshing motions in excited tanks［J］.Journal of Computational Physics，2004，196(1):53-87.

［12］Frandsen J B，Borthwick A G L.Simulation of sloshing motions in fixed and vertically excited containers using a 2-D inviscid sigma-transformed finite difference solver［J］.Journal of Fluids and Structures，2003，18(2):197-214.