MIMO无线通信系统容量研究

孙会楠

(哈尔滨华德学院 电子与信息工程学院, 黑龙江 哈尔滨 150025)

多输入多输出技术(MIMO)是无线通信领域中的重大技术性突破。它是指无线通信信号的发射端和接收端分别使用多个天线，使信号通过多条路径传送和接收，从而改善通信质量。MIMO是4G通信系统的核心技术，MIMO系统在不增加使用成本和技术难度的情况下，能够大幅度改善通信系统的信道容量，和传统的单输入单输出(SISO)系统相比有着显而易见的优势。因此，MIMO技术在未来的无线通信领域有着举足轻重的地位[1]。

本文首先推导了MIMO信道容量的计算公式，其次应用MATLAB软件对不同条件下的信道容量进行了仿真分析，并和单天线(SISO)系统、单输入多输出(SIMO)系统、多输入单输出(MISO)系统的信道容量进行对比，最后证明MIMO系统的优越性。

1 传统通信系统的信道容量

1.1 SISO系统的信道容量

对于高斯信道，发射端发射的总功率为P，噪声功率为σ2，则信道的香浓容量为

(1)

式中ρ=P/σ2，表示接收端获得的信噪比。对于参数不变的单天线系统，在某一时刻具有固定的信道复数增益h的SISO信道容量可表示为

C=lb(1+ρ|h|2) 。

(2)

当信噪比较大时，信道容量随信噪比的增加而增加。它们之间成对数关系，大约ρ每增加3 dB就可以使C增加1 bit/(s·Hz)。

对于随机信道系数，式(2)所描述的信道容量也可以是一个随机变量。此时可以得到SISO系统的遍历容量[2]：

(3)

图1为所描述的SISO信道容量仿真结果，收发天线数目均为1。由图1可知，信道容量仅随信噪比(SNR)的增加而增加。

图1 SISO系统的信道容量

1.2 SIMO系统的信道容量

(4)

C=lb(1+nRρ)。

(5)

与SISO系统相比，SIMO系统的分集增益为nR。图2所示为所描述的SIMO信道容量的仿真结果，接收天线数目分别为1、3、5、7、9。由图2可知，信道容量不仅随信噪比(SNR)增加而增加，还随接收天线数量的增加而增加。但如果天线数量达到了一定的程度，此时再增加天线数量，信道容量增加的幅度就十分有限。

图2 SIMO系统的信道容量

对于随机信道系数，该信道容量为

(6)

1.3 MISO系统的信道容量

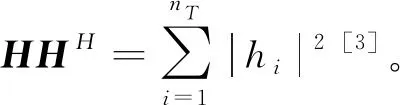
(7)

C=lb(1+ρ) 。

(8)

由式(8)可以看出，MISO信道容量并没有受到分集增益的影响，这是因为发射的总功率被平均分配到了各个发射天线上的缘故。图3所示为所描述的MISO信道容量的仿真结果，发射天线数目分别为1、3、5、7、9。由图3可知，信道容量不仅随信噪比(SNR)增加而增加，还随接收天线数量的增加而增加。但相对于SISO系统的容量增加的很少，当天线数量大于3时，再增加其数量对信道容量并没有明显的改善。

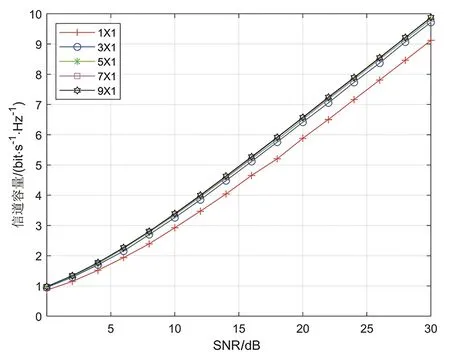
图3 MISO系统的信道容量

对于随机信道系数，该信道容量为

(9)

2 MIMO系统的容量分析

2.1 MIMO信道容量推导过程

图4为 MIMO系统框图。其中，发射天线数目为nT，接收天线数目为nR。假设信道为nR×nT维矩阵H。其中，Hi,j表示第i个发射天线到第j个接收天线之间的衰落系数；发射端发射的信号为nT×1维列向量x，xi表示第i个天线上发射的向量；接收端接收的信道噪声为nR×1维列向量n，噪声模型为独立分布的零均值的复高斯白噪声，方差为δ2[4]。

图4 MIMO系统框图

对于图4所示的系统，可表示为

y=Hx+n。

(10)

发射端无法获取信道状态信息，所以通常情况下每个发射端发射的信号功率是相同的，假设发射端发射的信号总功率为P，则单个发射端的发射功率为P/nT。由此可以推导出发射信号的协方差矩阵为

RXX=E(XXH)，

(11)

式中P=Trace(RXX)，这是由于发射功率受限所致。通过信息论的分析方法可以得出，发射信号的最佳分布模型为高斯分布，即发射信号均为高斯变量且互相独立。根据一般情况下高斯分布的特性可得

(12)

假设接收端接收到的信号功率等于发射的总功率，忽略其他因素造成的衰落等不利影响，则可以利用信道矩阵的奇异值(SVD)分解推导得出MIMO信道容量。根据SVD分解法，对H进行分解可得

H=UDVH，

(13)

式中：U和V均为酉矩阵，满足UUH=InR,VVH=InT；D为对角矩阵，是矩阵HHH特征值的算术平方根。将式(13)代入式(10)可得

y=UDVHx+n，

(14)

在式(14)的两边分别乘以UH，可得

UHy=DVHx+UHn，

(15)

式中VHx、UHn与x、n的统计特性完全一致，故该系统可以等效为i个SISO系统的集合。对于这种系统，其等效的系统模型如图5所示。

图5 MIMO的等效系统模型

(16)

式中Pyi为第i个子信道接收端接收到的信号功率。通过前边假设的两个条件可得

(17)

因此信道容量为

(18)

假设m=min(nT,nR)，特征值和特征向量之间的关系为

(λIm-W)y=0,y≠0，

(19)

式中W是威沙特(Wishart)矩阵，其定义为

(20)

当且仅当λIm-W为奇异矩阵时，λ是W的一个特征值，因此可得

det(λIm-W)=0。

(21)

通过查找式(20)的根，得到信道矩阵的特征值λ，因此式(21)左边的特征多项式为

p(λ)=det(λIm-W)，

(22)

式中m为式 (22)的幂次。对于det(λIm-W)的拉普拉斯最小项乘积式，每一行λIm-W的元素对应λ的一次乘积项[5]。由于系数为复数的m次多项式具有m个零点，故式(22)的特征多项式为

(23)

因此可得

(24)

用-nTσ2/P替换式(24)中的λ，可得

(25)

由式(18)得到固定信道系数的MIMO信道容量公式，即

(26)

因为HHH和HHH具有相同的非零特征值，所以信道矩阵H和HH也具有相同的信道容量。对于随机信道系数的MIMO系统，式(26)表示瞬时时刻的信道容量。

2.2 MIMO系统的各态历经容量

根据式(25)的定义，对于随机信道系数的MIMO系统，其遍历容量为[6]

(27)

式中：m=min(nT,nR)；符号EH[.]表示对信道矩阵求数学期望;矩阵W为

(28)

式(27)还可以写作[7]

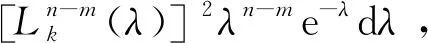
(29)

(30)

图6 MIMO系统的信道容量

图7所示为所描述的MIMO系统中断容量的累积分布函数的蒙特卡罗仿真结果，信噪比取30 dB。由图7可知，随着天线数量的增加，信道容量也不断增加；而且也可以看出，MIMO系统与单天线(1×1)系统相比信道容量有了很大幅度的提高。

图7 MIMO系统中断容量的累积分布函数

3 SISO、SIMO、MISO与MIMO信道容量的综合比较

为了综合比较分析传统通信系统和MIMO的信道容量，分别选择了1×1、3×1、5×1、1×3、1×5、3×3、5×5这七种收发天线构成方案。图8和图9分别为所述系统的各态历经容量和中断容量累积分布函数的综合比较仿真结果，仿真方法采用蒙特卡罗仿真法。假设信道系数服从瑞利分布，信噪比取30 dB，蒙特卡罗仿真的迭代次数为10 000。

图8 SISO、SIMO、MISO、MIMO系统的各态历经容量的综合比较

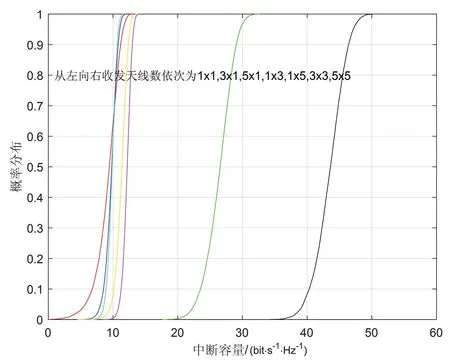
图9 SISO、SIMO、MISO、MIMO系统的中断容量累积分布函数的综合比较

通过观察收发天线数目为1×3和1×5的仿真曲线，可以总结出多个接收天线对信道容量造成的影响。接收端使用多个接收天线使信道获得了分集增益，这些增益降低了衰落的不利影响，并增大了接收端获得的信噪比(SNR)。因此SIMO系统的各态历经容量和中断容量相比SISO系统都获得了不小的提升。然而由于信噪比与信道容量成对数关系，导致分集增益产生的作用很快趋于饱和，信道容量提升的幅度也就十分有限。从两张仿真图中也可以看出，当接收天线从3个到5个时，信道容量并没有增大很多。

同理，通过观察收发天线数目为3×1和5×1的仿真曲线，可以总结出多个发射天线对信道容量造成的影响。当发射端无法获取信道状态信息时，就无法在多个发射天线中采用波束形成技术和自适应分配发射功率。并且发射的总功率还被平均分配到了各个发射天线上，导致信道中基本没有分集增益。这些因素使得MISO系统的中断容量得到提升，但各态历经容量却没有提升太多。从两张仿真图中也可以看出，3×1和5×1的各态历经容量曲线几乎是重合的。

通过观察收发天线数目为3×3和5×5的仿真曲线，可以发现MIMO系统在改善信道的各态历经容量和中断容量方面具有明显的优势，两张仿真图中曲线的数据远远超过其他曲线。这是因为MIMO系统结合并放大了SIMO系统和MISO系统各自的优点，从而优化了信道容量所致。实际上，当收发天线数目为nT=nR时，信道容量可以近似地看成和nT成正比，即

C≈nTlb(1+ρ)，

(31)

所以在理论上来说，只要收发天线的数量足够多，信道容量就可以趋近于无穷大。实际上这是不可能的，因为信道容量会受到物理信道自身的限制。

4 结论

MIMO系统突破了传统单天线系统(SISO)的瓶颈，并且信道容量相比一般的分系统(SIMO和MISO)有了明显的改善。通过仿真分析发现，在不考虑信道相关衰落特性的情况下，信道系数无论固定还是随机变化，信道容量受到收发天线数量和信噪比的共同影响。其中同一收发天线中，信道容量随信噪比的增大而增大；当收发天线数量增加时，信道容量也会增加，并且收发天线越多，信道容量随信噪比增大的幅度也会越大。因此，增大收发天线的数量，可以明显改善MIMO系统的信道容量。