基于Gauss-Hermite求积分卡尔曼滤波的SINS非线性初始对准方法

冉昌艳 程向红 王海鹏

(1 东南大学仪器科学与工程学院，南京210096)

(2 三峡大学计算机与信息学院，宜昌443002)

初始对准是捷联惯导系统(SINS)中的关键技术之一.当失准角较大时，常规的线性误差模型不能准确描述SINS 误差传播特性，需要采用更为精确的非线性误差模型，使得Kalman 滤波的应用受到限制.因此，各种非线性滤波方法不断得到应用.其中扩展卡尔曼滤波(EKF)，由于运算速度快和易于工程实现而应用最为广泛，但系统非线性特征较强时，局部线性化会带来很大的误差，甚至会导致滤波发散.无迹卡尔曼滤波(UKF)［1］对状态的概率密度函数用高斯分布进行近似，文献［2］将其与H∞滤波相结合，应用于有色噪声条件下的SINS大方位失准角初始对准，取得了较好的效果.容积卡尔曼滤波(CKF)［3］采用求容积规则选取容积点及其权重，运算量比UKF 小，精度和UKF 相当，郝燕玲等［4］将其用于SINS 动基座初始对准中，取得了远优于EKF 的对准精度和收敛速度.Gauss－Hermite 求 积 分 卡 尔 曼 滤 波(QKF)［5－7］是 一 种 基 于Gauss－Hermite 数值积分的递归贝叶斯滤波方法，已被证实比EKF 和UKF 具有更高的估计精度，且能够通过增加单变量Gauss 积分点而获得更高阶精度.

本文将QKF 应用到SINS 大方位失准角初始对准中，分别采用QKF 和比例对称采样UKF 进行SINS 动基座大方位角初始对准的仿真.仿真结果表明:当方位失准角较大时，QKF 对准精度比UKF高，且收敛速度快;而且当单变量的Gauss 点增加时，QKF 的对准精度还可以进一步的提高.

1 单变量Gauss 积分点配置方法

Gauss－Hermite 求积分公式为

式中，x 为一标量.式(1)是一个带权积分公式，其权函数为ω(x)=e－x2，m 个Gauss 点xi为Hermite多项式Hm(x)的零点，Hm(x)和m 个Gauss 系数Ai分别为

式(1)中的Gauss 积分公式具有2m－1 次代数精确度，m 值越大，精度越高.Gauss 点及其相应的Gauss 系数分别由式(2)和(3)求得，均与被积函数g(x)无关，且Gauss 型求积分公式是稳定的，也是收敛的，通常制成表格，因此可通过查表得到［8］.

设随机变量x 服从高斯分布N(0，1)，其函数g(x)的期望为E(g(x))，通过变量代换可变换成标准的Gauss－Hermite 求积分公式，即

利用Gauss－Hermite 求积分公式的Gauss 点和Gauss 系数，可将E(g(x))表示为

式中，ξi和ai可通过计算对称三角矩阵J 的特征值和特征向量的方法［7］得到.

当x～N(μ，σ2)时，令z～(x－ μ)/σ，则z～N(0，1)，因此讨论x～N(0，1)的Gauss－Hermite 求积分问题不失一般性.

2 多变量Gauss 积分点配置方法

假设x 是nx维随机向量，其各分量相互独立，且均服从N(0，1)高斯分布，每个分量Gauss－Hermite 求积分点取m 个.向量x 的函数g(x)的期望E(g(x))表示为

由于各分量相互独立，并将单个分量的m 个Gauss 点和其相应的系数代入，则可得到向量的Gauss 点和其对应的系数，即

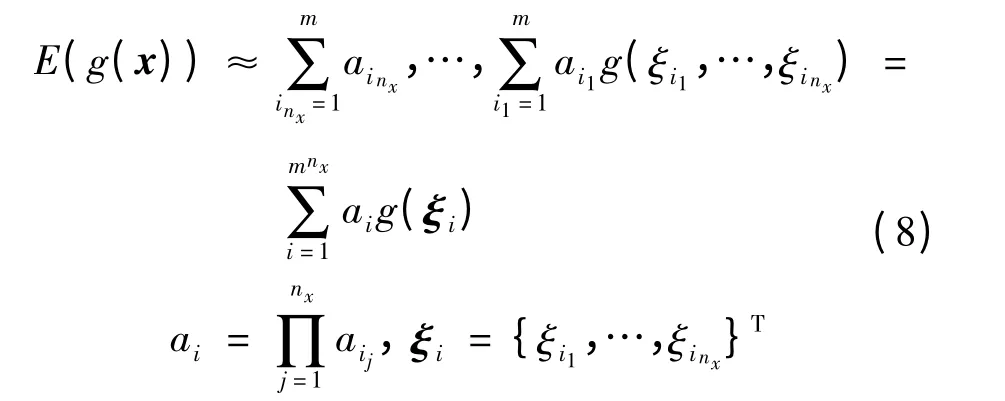
式中，ai和ξi为向量x 的第i 个Gauss 系数及Gauss 点向量;ξi1，…，ξinx为向量x 各分量对应的Gauss 点;{ξi1，…，ξinx}T表示由单个分量的Gauss点(共m 个)组合构成的Gauss 点向量(共mnx个);aij为Gauss 点ξij相对应的Gauss 系数;表示nx个分量的Gauss 系数aij的乘积.

若设单变量Gauss 点数为m，则多变量Gauss点数L=mnx，多变量的Gauss 点和Gauss 系数可以由单变量的Gauss 点进行Kronecker 张量积［9］扩展得到.

3 QKF 求积分卡尔曼滤波算法

考虑如下具有加性噪声的非线性系统方程和观测方程:

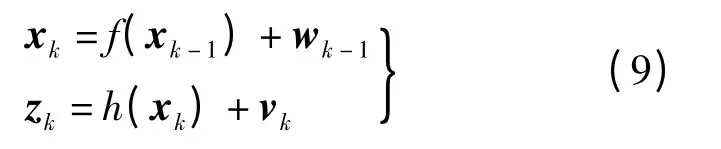
式中，xk为nx维状态向量，其各分量独立，且服从高斯分布;zk为nz维观测向量;f(·)和h(·)分别为非线性的状态函数和量测函数;wk和vk分别为过程噪声和量测噪声，且满足

式中，δkj为δ 函数.QKF 算法如下［5，7，10］:

1)初始化状态变量及其均方差

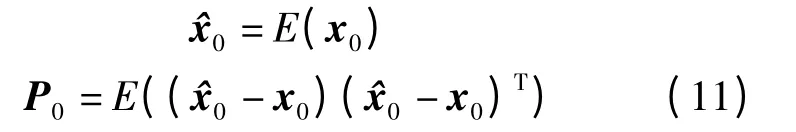
2)时间更新

分解前一步的方差阵为

计算高斯积分点，即

通过非线性状态函数传播的高斯积分点为

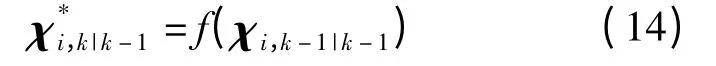
状态一步预测为

一步预测方差阵为

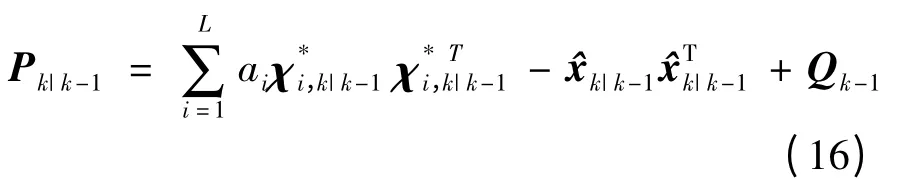
3)量测更新

一步预测方差阵分解为

一步预测状态高斯积分点为

通过非线性量测函数传播的量测高斯积分点为

一步预测量测值为

一步预测量测方差阵为

一步预测协方差阵为

卡尔曼增益为

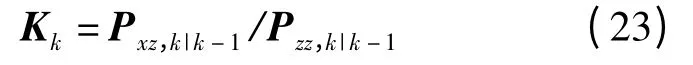
状态更新为

状态方差阵更新为

根据参考文献［11］中简化的UKF 方法，类似地，也可以将上述QKF 算法在量测方程为线性方程时予以简化，设

将量测更新步骤中式(17)～(20)简化为

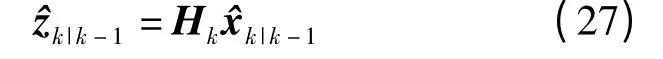
式(21)简化为

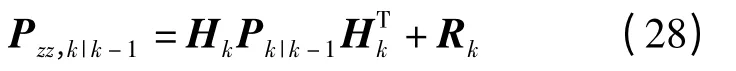
式(22)简化为

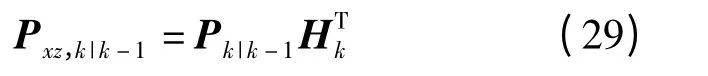
上述滤波算法中，ai，ξi，L 分别为多变量的Gauss 系数、Gauss 点向量以及总的Gauss 点数.

4 SINS 大方位失准角非线性误差模型

理想导航坐标系(n 系)与实际SINS 模拟的数学平台坐标系(c 系)之间的关系可以用姿态误差矩阵Ccn来表示，设φe，φn，φu分别为n 系至c 系的数学平台误差角，即东向、北向、天向姿态失准角.当φe和φn均为小量时，Ccn可简化为［2，4］

速度误差方程为［4，11］

大方位失准角姿态误差方程为［4，11］

定义系统状态向量为

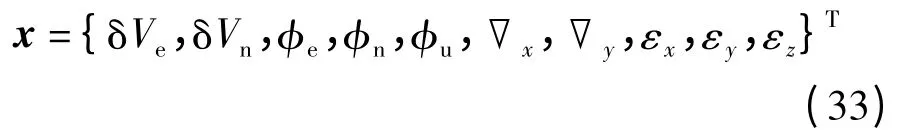
噪声向量为

观测量取量测速度之差，即z =［δVe，δVn］T，则SINS 非线性滤波模型为

式中，H= [ I2×202×8];v 为量测噪声，假设为零均值高斯白噪声.该滤波模型中状态方程为非线性，观测方程为线性，可通过四阶龙格库塔方法进行离散化处理后，采用简化QKF 算法进行滤波.

5 仿真分析

5.1 Gauss 积分点配置

3 点QKF 中状态向量单个分量的Gauss 点取3 个，即m=3，单变量的3 个Gauss 点和其对应的系数通过式(2)、(3)和(6)求出，分别为

如果状态向量有10 个分量，即nx=10，由式(8)将单变量的Gauss 点和系数通过张量积法扩展到10 维的Gauss 点向量及其相应的系数，则L =310，如果状态向量维数nx=5，则L=35.

5 点QKF，即m=5，单变量的5 个Gauss 点和其对应系数分别为

如选取状态向量维数nx=5，则L=55.

7 点QKF，m =7，单变量的7 个Gauss 点和其对应系数分别为

选取状态向量维数nx=5，则L=75.

5.2 仿真条件

航行速度为10 m/s，初始速度误差为0.1 m/s，匀速直航，航向、纵摇、横摇的摇摆幅值分别为2.5°，2.5°和12°，相应的周期分别为6，8 和10 s，姿态更新周期为0.01 s，滤波周期为1 s，陀螺仪3个方向的常值漂移设为0.05 °/h，噪声设为0.15°/h，加速度计偏置设为5 ×10－4g，噪声设为1.5 ×10－3g，初始位置为北纬32°、东经118.8°，初始航向角、纵摇角、横摇角均为0°，初始水平失准角均设为1°，初始天向失准角为100°.

设滤波器的初始条件为

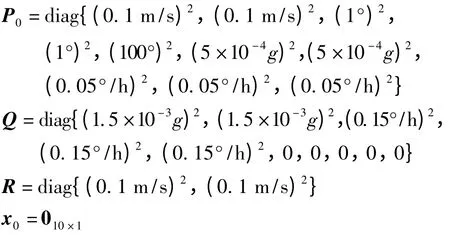
5.3 仿真结果

根据5.2 节仿真条件，分别采用比例对称采样UKF(α =0.01，k =－7，β =2，n =10)［11］和3 点QKF 进行SINS 动基座初始对准仿真，仿真时间为600 s，仿真过程中进行反馈修正.

由于2 个水平失准角的估计误差曲线相近，故只给出天向和北向的失准角估计误差曲线，如图1所示.

图1(a)中，当仿真时间为200 s 时，QKF 的天向失准角估计误差约为119′，UKF 的天向失准角估计误差约为997′，当仿真时间为600 s 时，精度差值达到479′，QKF 的天向失准角估计精度明显高于UKF.另外，当仿真时间为200 s 时，QKF 基本收敛，而此时UKF 还未收敛，QKF 收敛速度也要快于UKF.

图1 UKF 与3 点QKF 天向和北向失准角估计误差

在水平失准角估计误差方面，2 种非线性滤波算法比较接近，估计误差均很小，收敛速度均较快.图1(b)中，当仿真时间为600 s 时，QKF 的北向失准角估计误差约为3.7′，UKF 的北向失准角估计误差约为3.8′，QKF 的水平失准角精度略高于UKF;同样地，当仿真时间为30 s 时，QKF 基本收敛，而此时UKF 还未收敛，QKF 收敛速度快于UKF.

仿真还发现，随着初始天向失准角增大，两者收敛速度均会变慢，但QKF 的收敛速度要快于UKF;在精度方面，当初始天向失准角小于30°时，两者对准精度差别较小，随着初始天向失准角增大，两者对准精度均会变差，QKF 的精度变化幅度小于UKF，两者精度差距逐渐变大，如图2所示.

Gauss－Hermite 数值积分公式具有2m－1 次代数精确度，即3 点QKF 中的Gauss 积分代数精度能够达到5 阶，而UKF 中的积分代数精度最高为3阶.初始天向失准角较小时，非线性程度不深，两者对系统非线性的跟踪都较好;当初始天向失准角较大时，非线性程度加深，QKF 积分精度高于UKF，对系统非线性的跟踪要好于UKF.UKF 和QKF 虽然从原理上说都是用离散点逼近非线性模型，但UKF 相对于QKF 来说，在非线性较强时，统计特性差，逼近或者拟合函数误差较大，文献［12］中证明了UKF 是稀疏网格QKF 的子集.

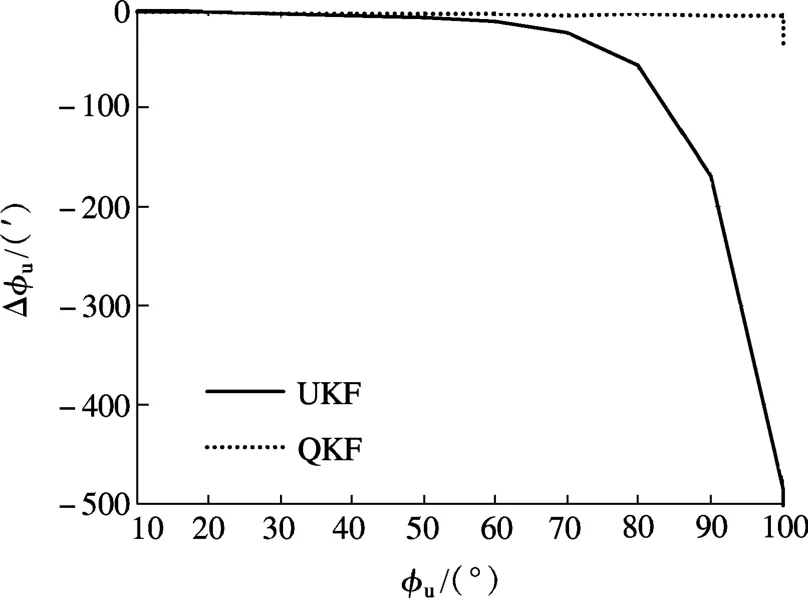
图2 UKF 与3 点QKF 天向失准角估计误差

为了说明单个分量Gauss 点配置数目对对准精度和速度的影响，分别选用3，5，7 个Gauss 点的QKF 进行仿真比较.为降低计算量，对滤波器进行降维处理，选用10 维状态量的前5 个作为状态量，将陀螺和加速度计的常值漂移放入噪声阵w 中，其他仿真条件不变.同样地，给出初始天向失准角为100°时的天向失准角估计误差和北向失准角估计误差曲线，分别如图3和图4所示.

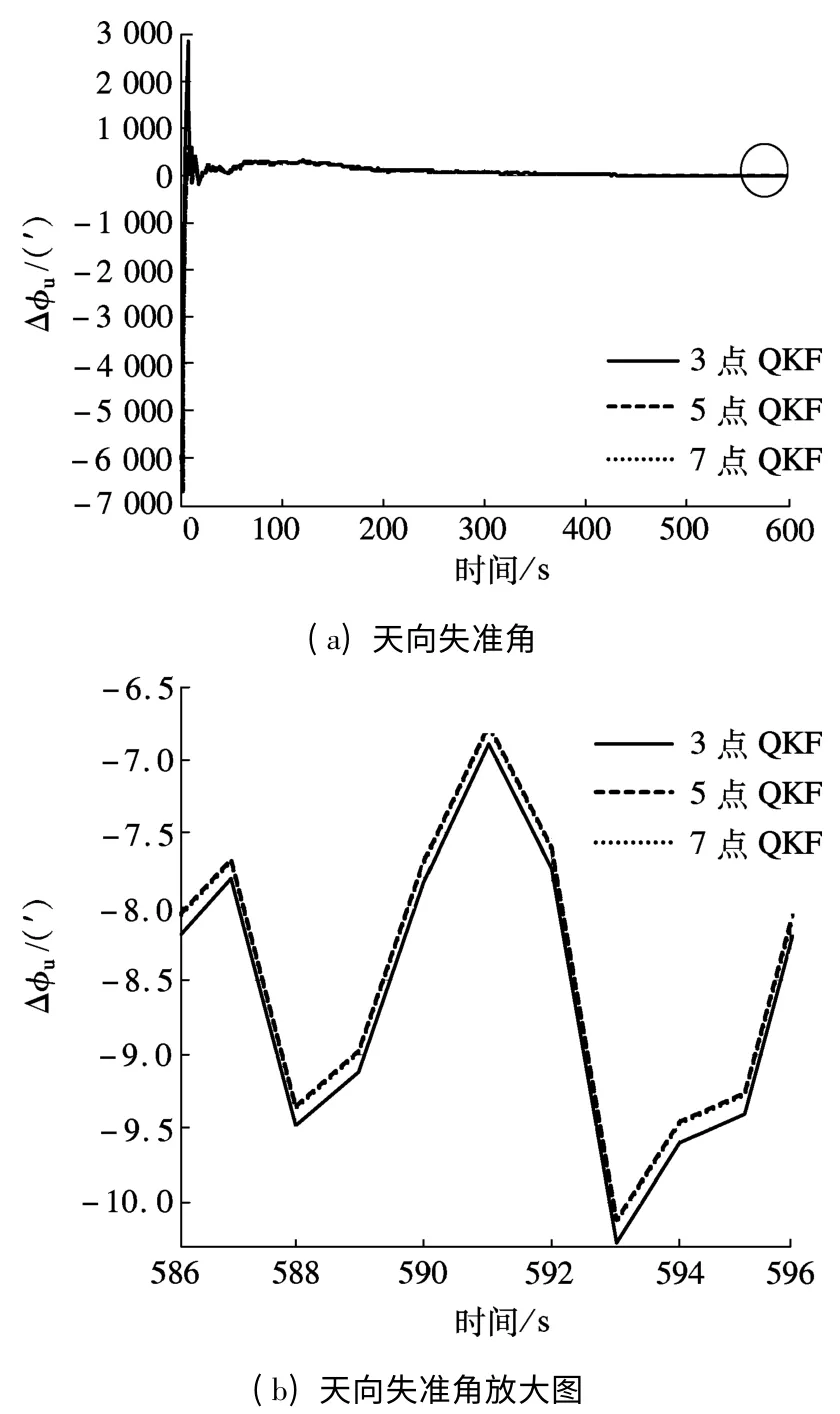
图3 不同点数QKF 天向失准角估计误差

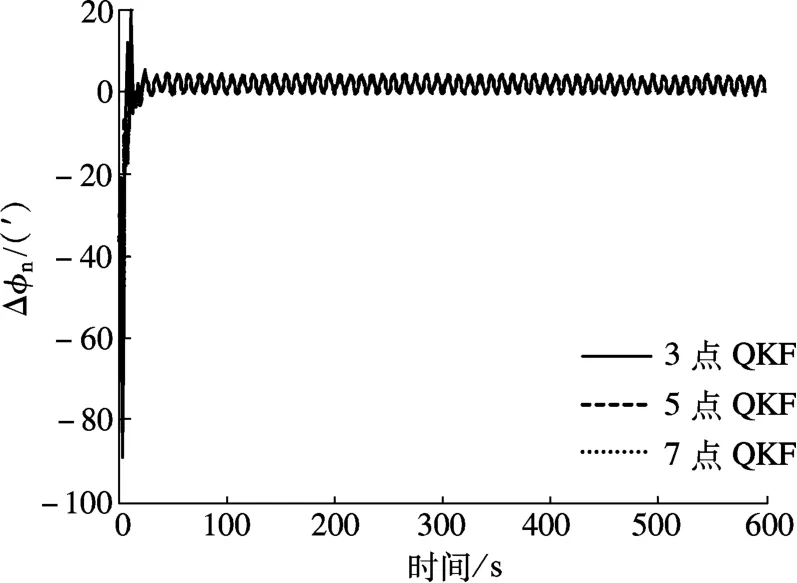
图4 不同点数QKF 北向失准角估计误差

图3(b)为图3(a)圈中部分放大图.图3表明3 点、5 点和7 点QKF 的天向失准角估计误差曲线非常接近，5 点和7 点QKF 曲线基本重合，从放大图中来看，其对准精度均要高于3 点QKF，但差别不大;三者收敛速度没有很大的差别.

图4中3 种点数的QKF 北向失准角估计误差均很小，三者曲线基本重合，3 点、5 点和7 点QKF中的Gauss 积分代数精度分别为5 阶、9 阶和13阶.仿真结果表明了在所设仿真条件下，虽然5 点、7 点QKF 的天向失准角估计精度高于3 点QKF，但其运算量增加很快，而大于5 点QKF 的精度和收敛速度差别不大，因此权衡计算量和对准精度，3点QKF 是较好的选择.

6 结语

本文采用Gauss－Hermite 求积分卡尔曼滤波方法对SINS 动基座下的大方位失准角初始对准进行了仿真研究.分析了Gauss 点和Gauss 系数的单变量配置及多变量配置方法，仿真分析表明:在相同仿真条件下，当初始天向失准角较大时，3 点QKF的天向失准角估计误差远小于比例对称的UKF，其估计收敛速度也快于UKF;而且随着单变量Gauss 点数的增加，QKF 对准精度会提高，但运算量也相应增大很多，需综合考虑对准性能和计算量.本方法的不足之处是运算量很大，滤波器的执行时间主要由Gauss 点的点数决定，尤其是状态维数较大时，其实用性会受到限制.文献［12］提出稀疏网格积分卡尔曼(SGQKF)可以大大减小多变量Gauss－Hermite 求积分的Gauss 点数，且有着与QKF相近的滤波精度，后续研究拟采用稀疏网格理论对多变量Gauss 点进行优化，将SGQKF 用于SINS 初始对准中.

References)

［1］Julier S，Uhlmann J，Durrant－Whyte H F.A new method for the nonlinear transformation of means and covariances in filters and estimators［J］.IEEE Transactions on Automatic Control，2000，45(3):477－482.

［2］Zhou Benchuan，Cheng Xianghong.Robust UKF algorithm in SINS initial alignment［J］.Journal of Southeast University:English Edition，2011，27(1):56－60.

［3］Arasaratnam I，Haykin S.Cubature Kalman filters［J］.IEEE Transactions on Automatic Control，2009，54(6):1254－1269.

［4］郝燕玲，杨峻巍，陈亮，等.基于SRCKF 的水下航行器动基座初始对准技术［J］.华中科技大学学报:自然科学版，2012，40(2):123－127.

Hao Yanling，Yang Junwei，Chen Liang，et al.Initial alignment method of the dynamic base for underwater vehicles using SRCKF［J］.Journal of Huazhong University of Science and Technology:Natural Science Edition，2012，40(2):123－127.(in Chinese)

［5］Ito K，Xiong Kaiqi.Gaussian filters for nonlinear filtering problems［J］.IEEE Transactions on Automatic Control，2000，45(5):910－927.

［6］巫春玲，韩崇昭.平方根求积分卡尔曼滤波器［J］.电子学报，2009，37(5):987－992.

Wu Chunling，Han Chongzhao.Square－root quadrature Kalman filter［J］.Acta Electronica Sinica，2009，37(5):987－992.(in Chinese)

［7］Arasaratnam I，Haykin S，Elliott R J.Discrete－time nonlinear filtering algorithms using Gauss－Hermite quadrature［J］.Proceedings of the IEEE，2007，95(5):953－977.

［8］孙志忠，袁魏平，闻震初.数值分析［M］.3 版.南京:东南大学出版社，2002:225－233.

［9］Fernandez－Prades C，Vila－Valls J.Bayesian nonlinear filtering using quadrature and cubature rules applied to sensor data fusion for positioning［C］//IEEE International Conference on Communications.Cape Town，South Africa，2010:1－5.

［10］Arasaratnam I，Haykin S.Square－root quadrature Kalman filtering［J］.IEEE Transactions on Signal Processing，2008，56(6):2589－2593.

［11］严恭敏，严卫生，徐德民.简化UKF 滤波在SINS 大失准角初始对准中的应用［J］.中国惯性技术学报，2008，16(3):253－264.

Yan Gongmin，Yan Weisheng，Xu Demin.Application of simplified UKF in SINS initial alignment for large misalignment angles［J］.Journal of Chinese Inertial Technology，2008，16(3):253－264.(in Chinese)

［12］Jia Bin，Xin Ming，Cheng Yang.Sparse－grid quadrature nonlinear filtering［J］.Automatica，2012，48(2):327－341.