螺旋槽干气密封气膜刚度测试与稳定性分析
2013-09-10丁雪兴张海舟
丁雪兴,张海舟,苏 虹,赵 芳,李 驰
(1.兰州理工大学 石油化工学院,兰州730050;2.湖北天力敏科技有限公司,湖北 襄阳441057)
近年来,由于干气密封在稳定性方面要求越来越高,而气膜刚度的稳定性是保证干气密封在稳定性的关键因素,因此关于气膜刚度的研究显得尤为重要。Green等[1]用有限体积法同步的解润滑方程和动力学方程,得出了一些密封参数诸如转动惯量、转速、锥度、压力等对动力学稳定性的影响,给出了密封稳定运行临界转速。Miller等[2]对螺旋槽端面密封环在轴向和2个角向自由度上的运动加以分析,用直接数值频率响应法计算气膜的刚度和阻尼特性。Zhang等[3]建立了单自由度三维微扰运动方程,并用正交分解法求得密封环三维运动规律。刘雨川等[4]应用微扰方法和有限元法,对端面气膜密封三自由度微扰下,密封气膜的刚度和阻尼系数进行了数值求解。徐万孚等[5]设计制造了“W A n def 28型”螺旋槽干运行非接触气体密封并进行了动态与稳定性分析。冯向忠等[6]针对螺旋槽气体端面密封结构,用有限元法计算了密封端面的气膜压力分布及密封的气膜刚度和泄漏量等特性参数。王之栎等[7]用有限元方法计算了两个端面的气膜刚度和阻尼。宫燃等[8]应用动态参数计算模型,对密封油膜的刚度和阻尼系数进行数值求解,分析了角微扰动与偏转力矩关系。杜兆年等[9]推导了干气密封螺旋槽内瞬态微尺度流动场的非线性雷诺方程,得到了气膜轴向刚度的近似解析解,并通过动态稳定性分析,获得了稳定性最佳的螺旋槽几何参数值。丁雪兴等[10]应用PH线性化方法及变分运算干气密封螺旋槽内瞬态微尺度流动场的非线性雷诺方程,通过动态稳定性分析,获得了不同介质粘度、压力和转速下稳定性最佳的螺旋角数。并用二阶非线性滑移边界条件推导出修正的广义雷诺方程,计算了不同转速和压力下气膜刚度数值[11]。张伟政等[12]建立了角向振动下气膜 -密封环系统的动力学模型,得到密封系统稳定时的密封结构参数范围,并分析了最佳稳定点和临界点振动响应。以上用数值模拟的方法对气膜刚度和阻尼的轴向、角向振动响应的研究较多,但用试验方法对干气密封的动态特性测试较少,尤其是在特性参数(轴向、角向气膜刚度和阻尼)和气膜位移的振动响应的测试较少,本文对轴向气膜刚度和气膜振动位移响应进行了测试,为用理论方法计算气膜刚度提供了一个数量级参考,并对实际的工程有指导作用。
1 干气密封测试技术
1.1 干气密封测试系统
干气密封测试系统包括硬件系统和软件系统。硬件系统主要包括:试验台,传感器,数据采集卡,计算机。软件系统主要由Labview软件开发的数据后处理系统。干气密封测试系统原理流程图,如图1所示:
干气密封测试系统试验台实物图如图2所示:
干气密封测试系统传感器接线实物图如图3所示:

图1 干气密封测试系统原理流程图Fig.1 Principle flow chart of dry gas seal Test system

图2 干气密封测试系统试验台实物图Fig.2 The physical map of test bed on dry gas seal test system

图3 传感器接线实物图Fig.3 The physical map of sensor wiring
1.2 气膜刚度的测试原理
1.2.1 气膜刚度的计算公式
气膜刚度等于端面气膜压力变化量与气膜轴向振动位移变化量的比值,如公式(1),
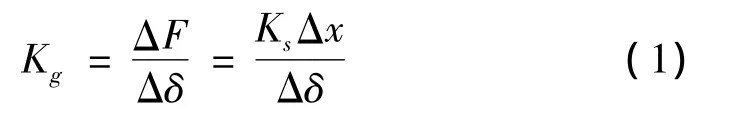
其中:Kg为气膜刚度,Ks为弹簧刚度,Δx为弹簧轴向振动位移变化量,即静环轴向振动位移,Δδ为气膜轴向振动位移变化量,ΔF为弹簧弹力的变化量,即端面气膜压力变化量,在本实验,干气密封测试系统选用刚度Ks=50 N/mm的弹簧。
1.2.2 气膜轴向振动位移变化量Δδ的测量
本实验选用ST-GL型高精度微型电涡流传感器来测量。传感器探头的安装剖面图如图4所示,将气膜振动传感器探头安装在静环端面相隔120o径向位置,传感器探头埋在静环端面内粘牢后,静环端面与探头端面一起研磨,使得静环端面与探头端面平齐。然后由传感器采集气膜轴向振动位移信号,经接口电路传送到计算机,再由Labview软件对数据进行后处理,气膜轴向振动位移变化量即被测得。
1.2.3 静环轴向振动位移变化量Δx的测量
静环轴向振动位移变化量的测量选用ST-GL型高精度微型电涡流传感器。传感器探头垂直安装在干气密封端盖端面相隔120o径向位置处,安装剖面图如图4所示。传感器探头埋在端盖端面内粘牢后,然后由传感器采集静环轴向振动位移信号,经接口电路传送到计算机,再由Labview软件对数据进行后处理,静环轴向振动位移变化量即被测得。
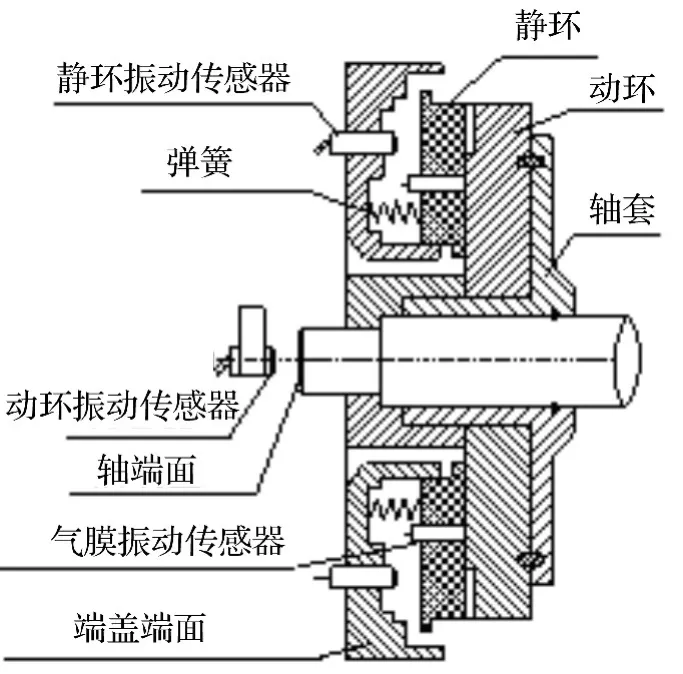
图4 传感器安装剖面图Fig.4 Sectional drawing of sensor installation
1.3 干气密封测试系统抗干扰采取措施
1.3.1 关键部件的选取
本实验是在气膜厚度极薄,振动量极小的微米级情况下进行测量,且在密封腔内部进行测量,所以测量难度极大,一般位移传感器难以对如此小的位移变化做出精确响应。所以本实验针对此类问题,选用高精度改进型微型传感器和采用了导磁性较好的硬质合金(碳化钨)作为动环材质进行微尺度测量试验研究。
1.3.2 具体抗干扰措施的采取
为了提高干气密封测试系统的精度,采取了一系列的抗干扰措施:降低干扰源的干扰,采用接地技术可以在一定程度上消除设备带来的干扰;提高传输通道的抗干扰能力,尽量缩短传导线的长度,并采用了屏蔽技术,所有传感器导线采用了高密屏蔽铜网,减少干扰磁场的影响;提高敏感测试设备的抗干扰能力,将原来输入阻抗为10M提高到了1G,保证干扰电流不会影响流入信号。
2 气膜刚度测试与稳定性分析
2.1 相同压力不同转速下的气膜刚度测试与稳定性分析
选用工况:压力P=0.4MPa,转速n分别为500 r/min,1 000 r/min,2 000 r/min,3 000 r/min。此工况下的气膜振动波形图和频谱分析图(如图5)和静环振动波形图和频谱分析图(如图6)。
2.1.1 气膜振动波形图和频谱分析
由图5可知:当压力P=0.4 MPa,转速n=500 r/min,1 000 r/min,2 000 r/min,3 000 r/min 时气膜振动位移变化量分别为 0.113 μm,0.094 μm,0.068 μm,0.057 μm。在相同压力下,随着转速的增加,气膜振动位移变化量随之减小,即在相同压力下,转速越大,气膜振动稳定性越好。
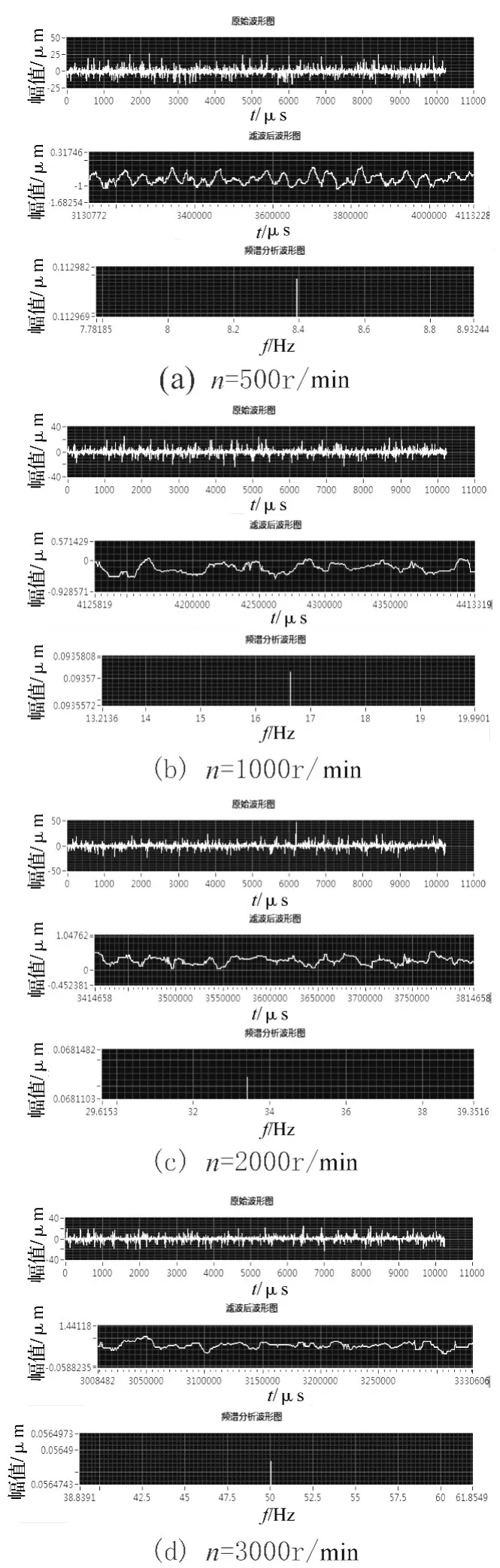
图5 气膜振动波形图和频谱分析图(P=0.4 MPa)Fig.5 Gas film vibration and spectral analysis diagram(P=0.4 MPa)
2.1.2 静环振动波形图和频谱分析
由图6可知:当压力P=0.4 MPa,转速n=500 r/min,1 000 r/min,2 000 r/min,3 000 r/min 时静环振动位移变化量分别为 30.3 μm,28.8 μm,29 μm,28.3 μm。
2.1.3 气膜刚度的计算
将2.1.1 和2.1.2 中数据代入公式(1),可得:当压力P=0.4 MPa,转速n=500 r/min,1 000 r/min,2 000 r/min,3 000 r/min时气膜刚度分别为0.013 4 kN/μm,0.015 3 kN/μm,0.021 3 kN/μm,0.024 8 kN/μm。在压力p=0.4 MPa下转速-气膜刚度的关系图如图7所示。
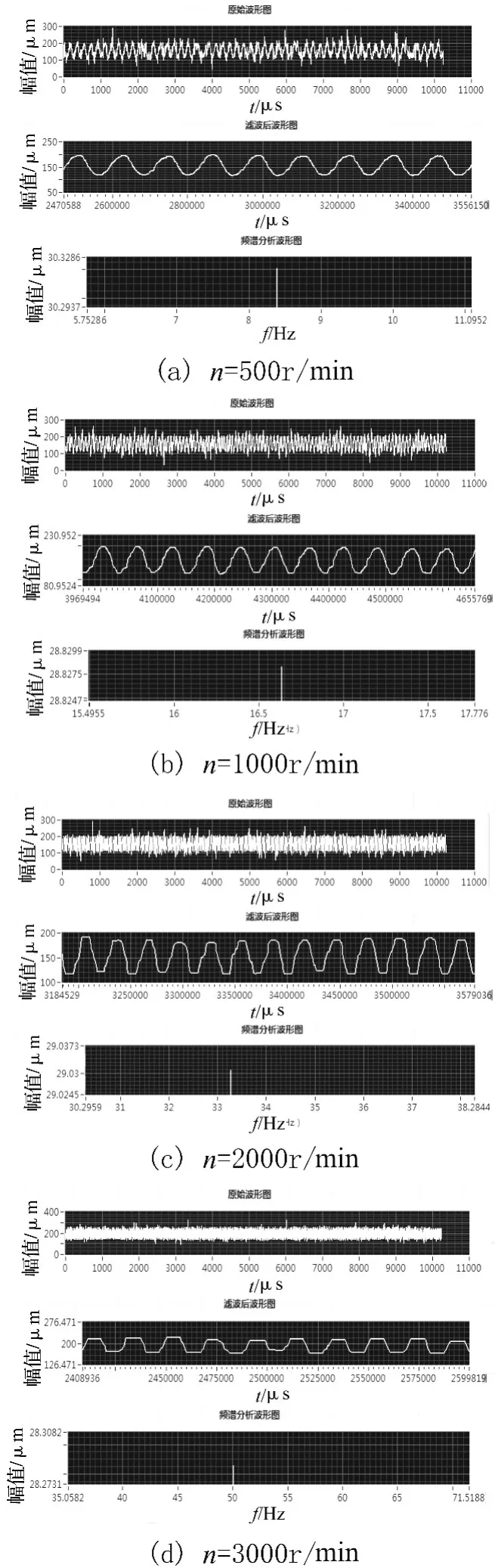
图6 静环振动波形图和频谱分析图(P=0.4 MPa)Fig.6 Stationary seal ring vibration and spectral analysis diagram(P=0.4 MPa)
2.1.4 气膜振动的稳定性分析
在相同压力下,随着转速的增加,气膜振动位移变化量随之减小,且由图7知:在相同压力下,气膜刚度随转速增大而增大。
这与在相同压力下,随着转速的增加,动压效果越好,气膜刚度越大,气膜振动的稳定性越好的机理相吻合。
2.2 相同转速不同压力下的气膜刚度测试与稳定性分
2.2.1 气膜振动波形图和频谱分析

图7 相同压力下转速-气膜刚度关系图Fig.7 The relationship chart of revolving speed and gas film in the same pressure
选用工况:转速n=2 000 r/min,压力P分别为0.2 MPa,0.3 MPa,0.5 MPa。此工况下的气膜振动波形图和频谱分析(如图8)和静环振动波形图和频谱分析(如图9)。

图8 气膜振动波形图和频谱分析图(n=2 000 r/min)Fig.8 Gas film vibration and spectral analysis diagram(n=2 000 r/min)
由图5(c)和图8可知:当n=2 000 r/min条件下,压力P分别为0.2 MPa,0.3 MPa,0.4 MPa,0.5 MPa 时气膜振动位移变化量分别为 0.104 μm,0.085 μm,0.068 μm,0.054 μm。在相同转速下,随着压力的增加,气膜振动位移变化量随之减小,即在相同转速下,压力的越大,气膜振动稳定性越好。
2.2.2 静环振动波形图和频谱分析
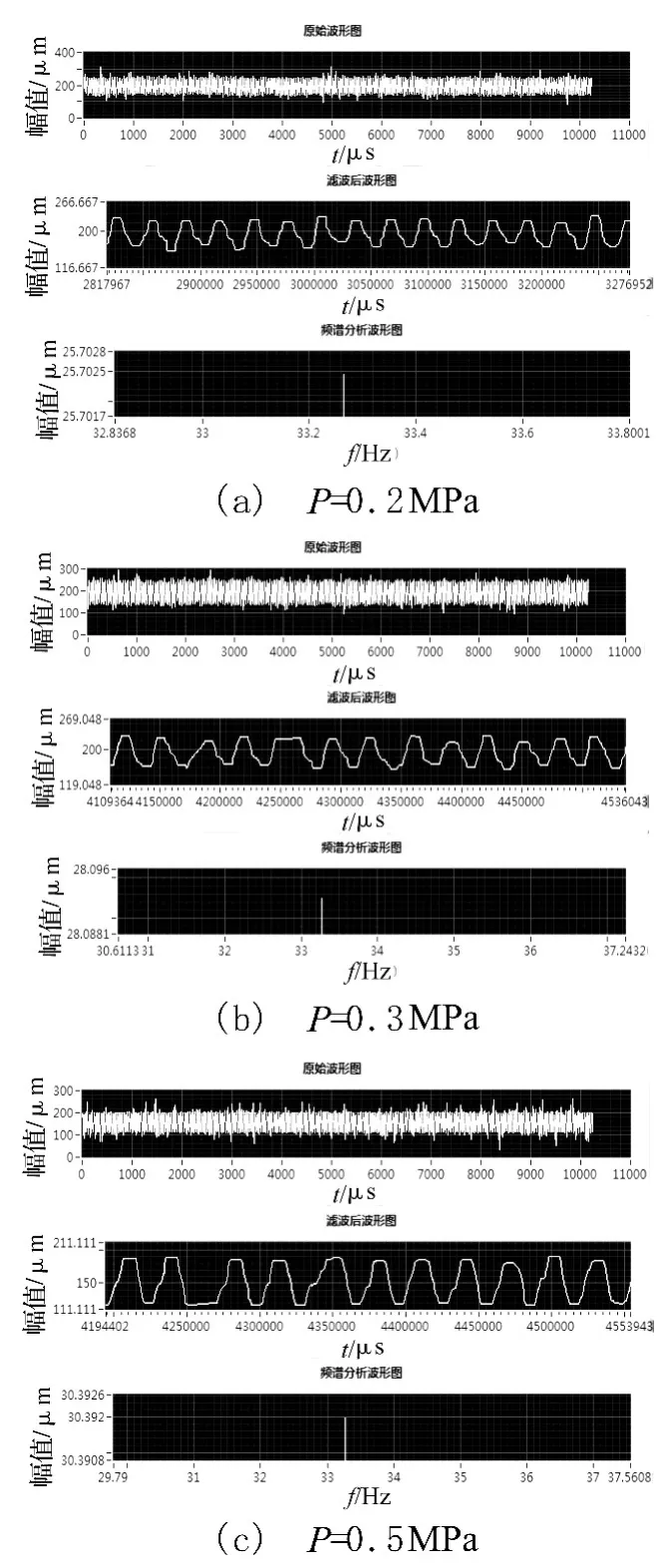
图9 静环振动波形图和频谱分析(n=2 000 r/min)Fig.9 Stationary seal ring vibration and spectral analysis diagram(n=2 000 r/min)
由图6(c)和图11可知:转速n=2 000 r/min,压力P分别为 0.2 MPa,0.3 MPa,0.4 MPa,0.5 MPa 时,静环振动位移变化量分别为 25.7 μm,28.1 μm,29 μm,30.4 μm。
2.2.3 气膜刚度的计算
将 2.2.1 和2.2.2 中的数据代入公式(1),可得:当转速n=2 000 r/min,压力P分别为 0.2 MPa,0.3 MPa,0.4 MPa,0.5 MPa 时气膜刚度分别为 0.012 4 kN/μm,0.016 5 kN/μm,0.021 3 kN/μm,0.027 9 kN/μm。在转速n=2 000 r/min下压力-气膜刚度的线性关系图如图10所示。
2.2.4 气膜刚度的稳定性分析
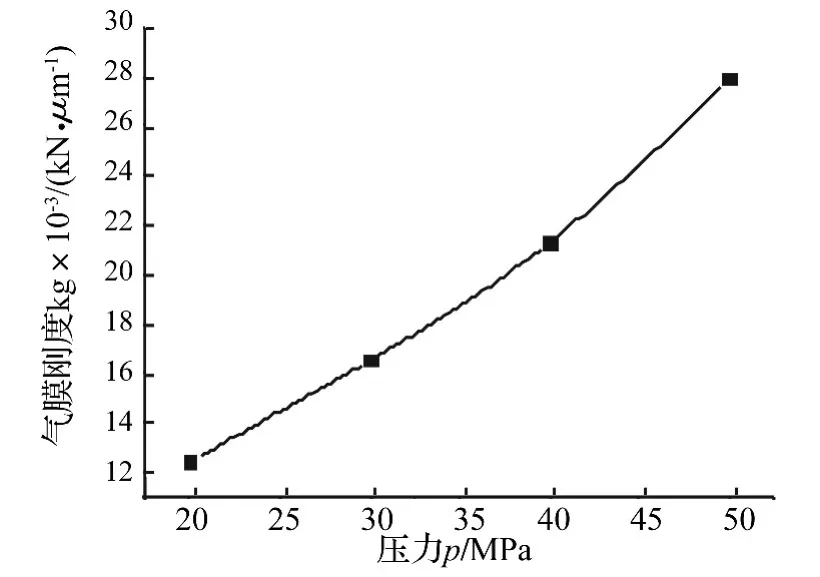
图10 相同转速下压力-气膜刚度关系图Fig.10 The relationship chart of pressure and gas film at the same revolving speed
在相同转速下,随着压力的增加,气膜振动位移变化量随之减小,气膜振动越稳定且由图10知:在相同转速下,气膜刚度随压力的增大而增大。这与在相同转速下,随着压力的增加,气膜开启力增大,气膜刚度也随之越大,气膜振动的稳定性越好的机理相吻合。
3 不同螺旋角对气膜刚的影响
在压力P=0.4 MPa,转速n=2 000 r/min条件下,当螺旋角 β=73.9°,β =74.1°时气膜振动和静环振动波形图和频谱分析图分别如图11和图12。

图11 不同螺旋角下气膜振动波形图和频谱分析图Fig.11 Gas film vibration and spectral analysis diagram on different spiral angle
由图11和图12可知:在压力P=0.4 MPa,转速n=2 000 r/min 条件下,当螺旋角 β =73.9°,β =74.1°时气膜振动位移变化量和静环振动位移变化量分别为0.147 5 μm,0.138 7 μm 和 31 μm 和 30.2 μm。代入公式(1),得螺旋角 β =73.9°,β =74.1°的气膜刚度分别为 0.010 5 kN/μm,0.010 9 kN/μm,又由 3.13 知 β=74°时气膜刚度为0.021 3 kN/μm。在P=0.4 MPa,转速n=2 000 r/min下螺旋角-气膜刚度的线性关系图如图13所示。
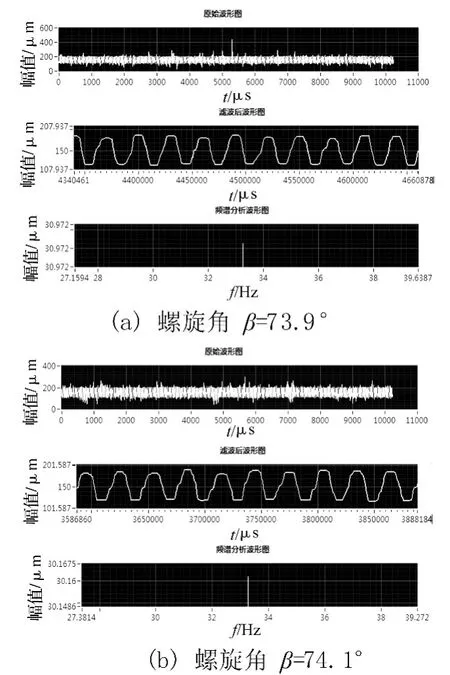
图12 不同螺旋角下静环振动波形图和频谱分析图Fig.12 Stationary seal ring and spectral analysis diagram on different spiral angle
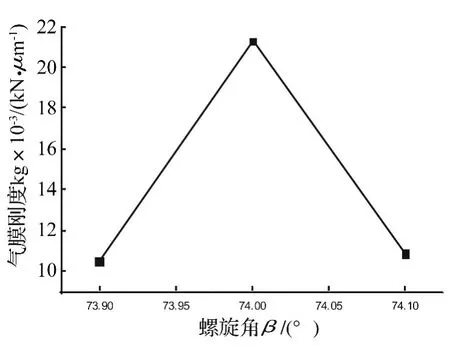
图13 螺旋角-气膜刚度的关系图Fig.13 The relationship chart of spiral angle and gas film stiffness
由图13知:特定的工况下,在试验所测试的三种不同螺旋角,当螺旋角β=74°时,气膜刚度最大,气膜振动的稳定性最好。由于在本试验中只测试了三种不同的螺旋角,所以不能得出螺旋角与气膜刚度的具体关系,但是可知气膜刚度值对螺旋角的变化很敏感,即气膜振动的稳定性对螺旋角的变化很敏感。因此选取合适的螺旋角可增加气膜振动的稳定性。
4 结论
本次试验工况:介质气体的压力变化范围0.2-0.5 MPa,转速变化范围为500-3 000 r/min,测得气膜刚度值的范围为 0.01-0.03 kN/μm,这与文献[11]中的理论计算值相符。由实验数据分析:气膜刚度随着压力的升高和转速的增大而增大,且气膜刚度分别与压力和转速的变化基本成线性关系;由试验知气膜刚度值对螺旋角的变化很敏感,因此选取合适的螺旋角可增加气膜振动的稳定性。这在理论计算和实际工程应用中对干气密封结构参数的优化有指导作用。
[1] Green I,Roger M.A simultaneous numerical solution for the lubrication and dynamic stability of noncontacting gas face seals[J].ASME J.Tribol.,2001,123(4):388-394.
[2] Mi1ler B,Green I.Numerical technique for computing rotor dynamic properties of mechanical gas face seal[J].ASME J.Tribol,2002,124:755-761.
[3] Zhang H J,Miller B A,Landers R G.Nonlinear modeling of mechanical gas face seal systems using proper orthogonal decomposition[J].ASME J.Tribol,2006,128(10):817-827.
[4]刘雨川,徐万孚,王之栎,等.端面气膜密封动力特性系数的计算[J].清华大学学报:自然科学版,2002,42(2):185-189.
LIU Yu-chuan,XU Wan-fu,WANG Zhi-li,et al.Dynamic coefficients for gas film face seal[J].Tsinghua Univ(Sci and Tech),2002,42(2):185-189.
[5]徐万孚,刘雨川,李广宇,等.螺旋槽干运行非接触气体密封的理论分析与试验[J].机械工程学报,2003,39(4):124-127.
XU Wan-fu,LIU Yu-chuan,LI guang-yu,et al.Theoretical analysis and experimental investigation of spiral groove dry running noncontacting gas seals[J],Journal of Mechanical Engineering,2003,39(4):124-127.
[6]冯向忠,彭旭东.螺旋槽干式气体端面密封的刚度和泄漏量研究[J].石油大学学报(自然科学版),2005,29(2):83-85.
FENG Xiang-zhong,PENG Xu-dong.Study of stiffness and leakage rate of spiral groove dry gas face seals[J].Journal of the University of Petroleum,2005,29(2):83-85.
[7]王之栎,刘国西,郭艳丽.反转轴间气膜密封振动过程分析[J].振动与冲击,2011,30(2):181-185.
WANG Zhi-li,LIU Guo-xi,GUO Yan-li.Vibration process analysis of a gas film seal in counter rotating shafts[J].Journal of Vibration and Shock,2011,30(2):181-185.
[8]宫 燃,葛如海,谢明祥.密封环扰动状态下稳定性分析及动态响应[J].振动与冲击,2011,30(8):179-182.
GONG Ran,GE Ru-hai,XIE Ming-xiang.Stability and dynamical characteristic investigation on seal under small disturbance[J].Journal of Vibration and Shock,2011,30(8):179-182.
[9]杜兆年,丁雪兴,俞树荣,等.轴向微扰下干气密封螺旋槽润滑气膜的稳定性分析[J].润滑与密封,2006(10):127-130.
DU Zhao-nian,DING Xue-xing,YU Shu-rong,et al.A stability analysis for lubricating gaseous film of the sprial grooved gas seals subjected to axial perturbation[J].Lubrication Engineering,2006(10):127-130.
[10]丁雪兴,王 悦,张伟政,等.螺旋槽干气密封润滑气膜角向涡动的稳定性分析[J].北京化工大学学报,2008,35(2):7-11.
DING Xue-xing,WANG Yue,ZHANG Wei-zheng,et al.A stability analysis for lubricating gaseous film of spiral grooved gas seals subjected to angular eddy motion[J].Journal of Beijing University of Chemical Technology(Natural Science Edition),2008,35(2):7-11.
[11]丁雪兴,蒲军军,韩明君,等.基于二阶滑移边界的螺旋槽干气密封气膜刚度计算与分析[J].机械工程学报,2011,47(23):119-124.
DING Xue-xing, PU Jun-jun, HAN Ming-jun,etal.Calculation and analysis of gas film stiffness in the spiral groove gas seal based on the second order slip boundary[J].Journal of Mechanical Engineering,2011,47(23):119-124.
[12]张伟政,俞树荣,丁雪兴,等.干气密封系统角向摆动的稳定性及其振动响应[J].振动与冲击,2011,30(3):96-99.
ZHANG Wei-zheng,YU Shu-rong,DING Xue-xing,et al.Stability analysis and vibratory response of angular wobbly in the system of dry gas seal[J].Journal of Vibration and Shock,2011,30(3):96-99.
