浅析CH-γ方程中解的求法
2021-10-19邹灵果
邹灵果
(厦门海洋职业技术学院,福建 厦门 361009)
0 引言
近年来,研究非线性方程的方法已趋于成熟,许多学者利用各种方法在研究一些典型的非线性方程中,得到了一些很有意义的解。其中行波解是非线性偏微分方程非常重要的一类解,并已经发现很多典型的非线性偏微分方程有丰富的行波解。例如,著名的KdV方程:ut-6uux+uuxxx=0[1]有光滑的孤立波解;CH方程:ut-uuxxt+3uux=2uxuxx+uuxx[2]有孤立尖波解等行波解;Fornberg-Whitham方程:ut-uxxt+ux=uuxx-uux+3uxuxx[3]在一定条件下会出现爆破的行波解。除此之外像Burgers方程、Sine-Gordon方程、KP方程等都有丰富的行波解。像辅助方程法[4](代数方法),广义椭圆方程法[5],F-展开法[6],和平面动力系统分支理论[7]都被运用到研究非线性偏微分方程领域中。这四种数学方法一直都是非线性分析很好的工具。本文利用W.Rui提出的一种改进的方法[8]——积分分支法来求解非线性偏微分方程。这种改进的方法不像分支理论那样需要涉及复杂的相图分析,它很容易就能够满足。为积分分支法在解非线性偏微分方程的应用奠定基础。
1 非线性偏微分方程的积分分支法
1.1积分分支法的概述
对一个给定的(n+1)维非线性偏微分方程:
E(t,xi,uxi,uxixi,uxixj,utt,…)=0(i,j=1,2,…,n),
(1)
积分分支法简单过程如下:
P(ξ,φ,φξ,φξξ,φξξξ)=0
(2)
这里μi(i=1,2,…n)是任意非零常数。
反复对(2)积分直到它变成下面的二阶非线性常微分方程:
G(φ,φξ,φξξ,φξξξ)=0
(3)
那么进行下一步。

(4)

(5)
这里的τ是参数。如果系统(4)是一个积分系统,那么方程(4)与方程(5)有如下相同的积分:
H(φ,y)=h
(6)
这里是积分常数。一般情况下,函数(6)满足下面关系:
y=y(φ,h)
(7)
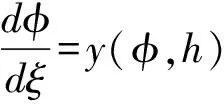
(8)
如果表达式(7)是一个分式,那么把(7)代入(5)的第一个方程并积分之,得到:
(9)

因为方程(1)的参数值和方程(6),(7)中的常数h是变化的,方程(8),(9)也是一样,所以叫这些积分表达式为积分分支。不同的积分分支相当于不同的行波解。以上为积分分支法的全部过程。
1.2积分分支法的改进
W.Rui[8]在积分分支法的基础上结合Jacobi椭圆函数积分对积分分支法进行了一些改进:
由系统(4)得到:
(10)
或者由系统(5)得到:
(11)
根据A,B,…,C或P,Q,…,R的取值结合表1、表2得到方程(1)的解。

表1 方程F′2=RF2+QF3+PF4的解

表2 方程F′2=RF2+QF3+PF4的参数选择
2 采用积分分支法求CH-γ方程的精确解
2.1对CH-γ方程的约化
首先对CH-γ方程:
ut+c0ux+3uux-α2(uxxt+uuxxx+3uxuxx)+γuxxx=0,
(12)
作变换,令u=φ(ξ)=φ(x-ct),其中,ξ=x-ct,x为波长,t为时间都是变量,c为波速为待定参数,
则方程(12)变形为:
(c0-c)φ′+3φφ′-α2(-cφ′′+φφ′′+3φ′φ′′)+γφ′′=0,
(13)
方程(13)两边对ξ积分得:
2(c0-c)φ+3φ2+2(α2c+γ-α2φ)φ′′-2α2(φ′)2=0,
(14)
令φ′=y,则(14)变成下面两个微分系统:
(15)
再令dξ=2(α2c+γ-α2φ)dτ,
(16)
则系统(15)变为:
由(17a)/(17b)得:
其中h为积分常数。

(21)
结合(16),(21)可以变形为:
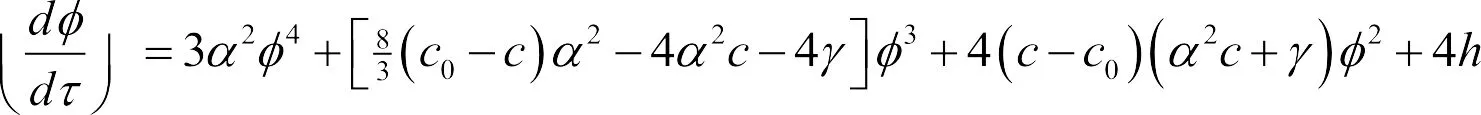
(22)
2.2求CH-γ方程的精确解
(1)求CH-γ方程的参数解
情形I:h=0
则方程(22)变形为:

(23)

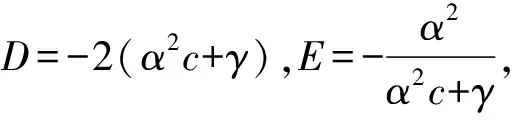
dξ=D(1+Eφ)dτ。
(24)

(25)
这里τ是参数,图1是其波形图。

图1 波参数解(25)波形图
图1b参数条件:α=1,γ=2,c=10,c0=2,ε=-1,τ=[-0.2…0.10609])
类似的结合表1和方程(24),得到方程(12)的解如下:
(26)
(27)
图2是解(27)的波形图。

图2 波参数解(27、33)波形图
图2b参数条件:α=2,γ=3,c=5,c0=5,τ=[-4.5302…4.5])
(28)
图3是解(28)的波形图。

图3 波参数解(28)波形图
图3b参数条件:α=4,γ=2,c=5,c0=2,ε=-1,τ=[-0.1005…5.3])
(29)
图4是解(29)的波形图。
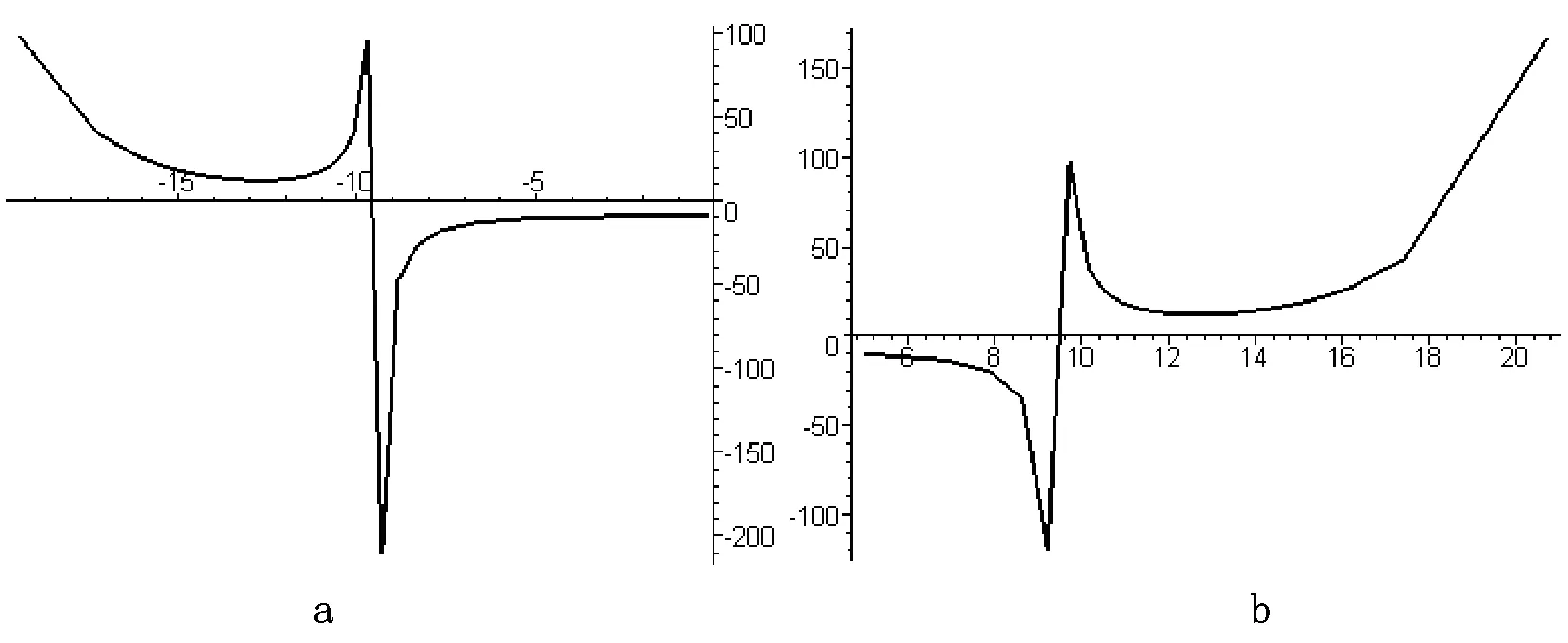
图4 波参数解(29)波形图
图4b参数条件:α=2,γ=3,c=1,c0=10,ε=-1,τ=[-2.93…4.8701])
(30)
图5是解(30)的纽子波与反扭子波的波形图。

图5 波参数解(30)波形图
(31)
图6是解(31)的波形图。

图6 波参数解(31)波形图
(32)
(33)
解(33)是孤立波解,图2是其波形图。
情形Ⅱ:h≠0

(34)
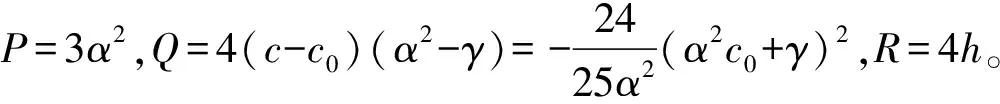
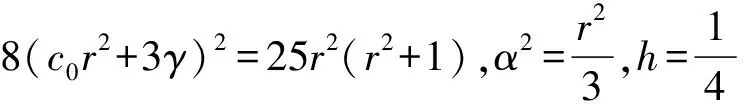
φ(τ)=sn(τ,r),
(35)
图7b参数条件:r=0.99,c0=5,γ=-0.8126146357,τ=[-29.52…23.45]

图7 波参数解(36)波形图
把方程(35)代入方程(26),两边积分,可得到方程(12)一个特殊的周期波参数解:
(36)
图7是其波形图。

(37)
图8是其波形图。

图8 波参数解(37)波形图
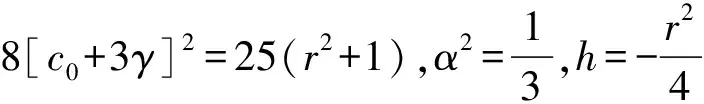
(38)

(39)
(2)求CH-γ方程的显式解
从方程(20),定义
(40)

(41)

(42)

(43)

(44)
把方程(44)分离变量两边积分得:

(45)


(46)
3 结论
本文采用积分分支法结合Jacobi椭圆函数积分在不同的参数条件下得出了方程(12)的多种参数行波解和一种显示解,包括纽子波解、反纽子波解、周期波解、孤立波解等行波解,并与原文献相比出现了一些新的结果。
