基于轴向模态应变能比法的三维桁架结构损伤定位方法

冯 坤，杨永春，郑 轶

(1.中冶东方工程技术有限公司建工所，山东 青岛 266555;2.中国海洋大学 工程学院，山东 青岛 266100;3.山东省科学院海洋仪器仪表研究所，山东 青岛266071)

我国是一个多自然灾害的国家，几乎每年都要发生地震、风灾、水灾等重大自然灾害，这些自然灾害对大型工程结构的安全造成了严重的威胁。高层建筑、大型桥梁、海洋平台等在其服役环境中受到设计载荷、腐蚀、材料老化等各种不利因素的影响，产生损伤积累、抗力衰退从而导致结构使用寿命的降低甚至完全破坏。没有被探测到的结构损伤将减弱结构的强度和刚度，可引发更大的结构损伤积累，导致结构的突然失效而造成重大事故。

由于海洋平台结构不能中断使用以及昂贵的造价，在役结构的安全评估方法应该是无损或微损的，目测是通常所用的无损检测方法，对于如构件断裂目测能够判定损伤。然而，对于材料老化造成的损伤，在不可靠近的区域或者被油漆、锈以及海洋生物覆盖着的损伤是很难利用目测检测损伤的，所以目测进行无损检测是不可靠的。其它无损检测技术，如X光检测、超声检测、工业CT等方法属于结构局部损伤检测方法，而这类技术仅仅用于损伤区域已知的情况。此外，这些技术还要求特殊的测试设备和专业人员，因此，这些方法对于海洋平台结构的无损检测是不方便的，并且是昂贵的。

基于动力特性的结构损伤识别检验方法近几十年来一直是学术界和工程界关注的热点。结构动态检测方法与传统的无损检测技术相比，具有信号易于提取、探测器可以安装在人们不易接近的构件部位(或者遥测)、操作起来简便快捷、经济等优点。该检测技术可连续或间隔的对结构进行检测，并可用来指导对损伤可疑部位的评估，提高检测效率。因此国内外许多研究领域的学者、专家都投入到这方面的研究工作之中。

海洋平台结构由于其高阶模态难以激起和测试，仅能识别出一阶或前几个低阶模态振型，因此，本文利用损伤前后结构动力特性的变化，构造合适的损伤指标用以指示损伤的存在、位置和程度。基于动力测试的损伤识别，利用少量低价模态进行损伤识别显得尤为重要。本文根据导管架海洋平台结构的杆单元应变特点，仅利用一阶、二阶模态参数，将出现明显的峰值点作为结构单元出现损伤的判别准则，对海洋平台进行损伤位置诊断，并通过四腿导管架海洋平台有限元数值模型、物理模型验证该方法的可行性和有效性。

1 基本理论

对于空间任一个杆单元，杆件的长度为l0，结构无损伤及有损伤时空间杆件变形后的长度分别为l1、l2，杆件轴向长度的变化量分别为:

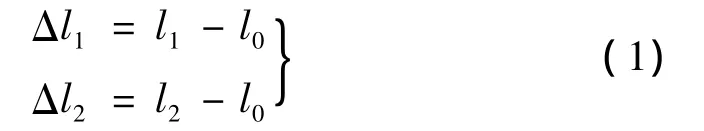
无损伤和有损伤时杆件的轴向应变分别为:

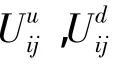
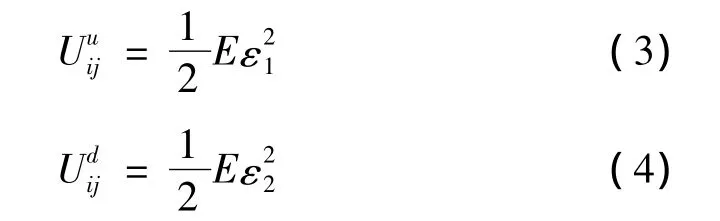
注意式(4)中的弹性模量E在理论上应取损伤后的弹性模量值，但对于损伤单元，其弹性模量是未知数，因而用损伤前弹性模量近似代替之。

定义轴向模态应变能比为:

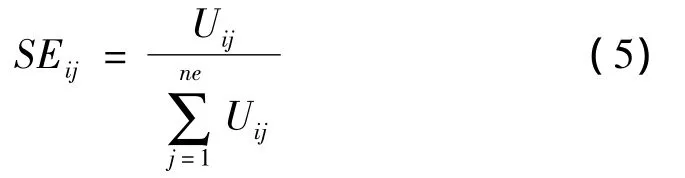
式中:ne为结构单元个数，选取轴向模态应变能比在损伤前后的差值作为定位参数ID，按定义，将损伤前后的轴向模态应变能比分别写为:

这样，损伤定位参数ID的表达式便写为:

其中:IDij指第j单元在i阶模态下的轴向模态应变能比在损伤前后的差值。当第k个单元发生损伤时，IDik的绝对值将大于任何其他未损伤单元的IDij(j≠k)的绝对值。如此通过检查所有单元对应的ID值，就能确定出结构的损伤区域。

为了更有效地诊断出损伤位置，可将N个测量模态的ID值累加，得到任一单元j在多个模态影响下的损伤定位参数值IDj如下:

2 数值模拟

2.1 有限元模型的建立

根据结构形状尺寸和材料特性，采用有限元分析软件 ANSYS10.0，建立海洋平台结构的有限元模型，该模型包括16个导管架柱单元，22个水平撑单元和16个斜撑单元，共有20个节点，54个单元，4个柱脚节点均约束全部自由度。如图1所示。材料弹性模量为E=2.07 ×1011Pa，泊松比为 0.3，密度为 7 800 kg/m3。将导管架海洋平台结构近似的看作三维桁架结构，横杆、竖杆、斜撑均采用link 8单元来模拟。link 8单元可用于模拟桁架、缆索、连杆、弹簧等，是杆轴方向的拉压单元。

用ANSYS有限元分析软件对该结构有限元模型进行分析可以得到前三阶模态振型，如图3所示，第一阶模态主要是在y方向的振动，频率为58.735 Hz，第二阶模态主要在 x方向上，频率为 79.419 Hz，第三阶模态主要是扭转方向的振动，频率为101.65 Hz。在以下的分析中，损伤工况既包括了单个损伤又包括了多个损伤的工况。

2.1.1 单损伤工况

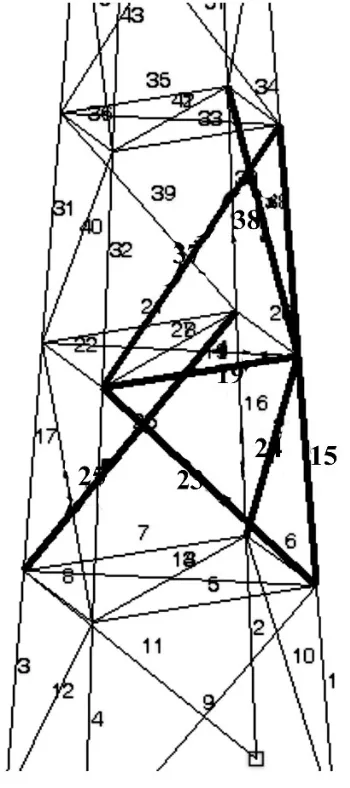
图2 六种工况下的构件损伤位置Fig.2 Approximately selected damaged members at different positions

图3 结构前三阶模态振型图Fig.3 Numerical model of the jacket platform

单损伤工况中考虑了三种具有代表性的工况，模拟的损伤单元是:X方向水平撑19单元，XZ方向的斜撑23单元，YZ方向的斜撑38单元。所有构件模拟的损伤均减小了20%和50%的刚度两种情况。

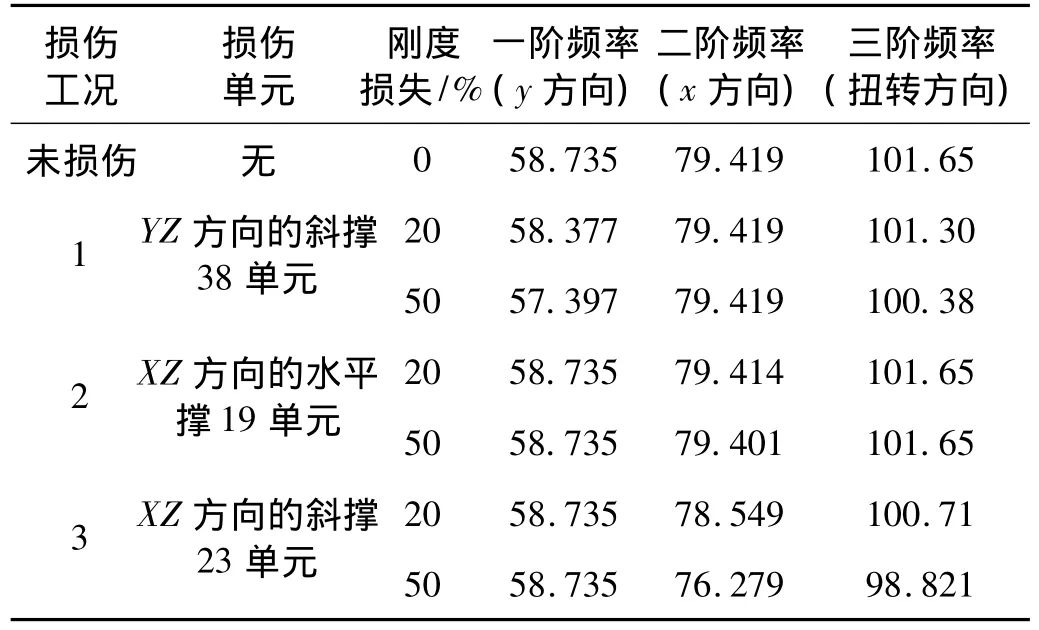
表1 结构单损伤工况及损伤前后的固有频率(单位:Hz)Tab.1 Natural frequency results of one damage scenario

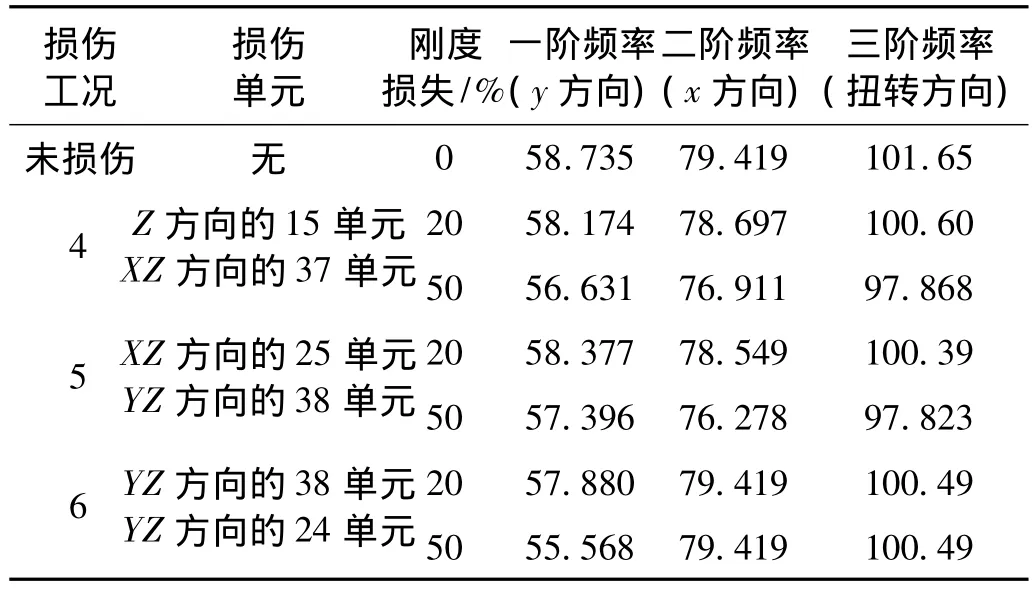
表2 结构多损伤工况及损伤前后的固有频率(单位:Hz)Tab.2 Natural frequency results of multi damage scenario

2.1.2 多损伤工况

多损伤工况分析了不同方向构件同时发生损伤的情况。下面的研究就是在验证本节提出的新指标在多损伤工况下的损伤定位能力。三种多损伤工况都包括斜撑，分别发生在:单元 24、25、37、38。同样的，所有的损伤构件刚度损失了20%和50%两种情况。表2总结了这三种损伤工况。同时也列举了结构损伤前后的前三阶固有频率。

2.2 模拟损伤工况及诊断结果分析

对于空间结构，当一根或多根杆件出现损伤时，损伤后连接损伤杆件的节点位移自然会发生较大变化，而连接其他杆件的节点位移则变化不大。因此，可利用轴向模态应变能比法对损伤杆件进行定位。

图2列出各种工况损伤位置。模拟的损伤工况是:X方向水平撑单元19;XZ方向的斜撑单元23;YZ方向的斜撑单元38;Z方向的柱单元15和XZ方向的斜撑单元37同时损伤;YZ方向的斜撑单元24和单元38同时损伤;XZ方向的斜撑单元25和单元38同时损伤。所有模拟的构件损伤均减小了20%和50%的刚度两种情况。单元38损伤20%和50%时损伤定位结果如图3、图4所示。

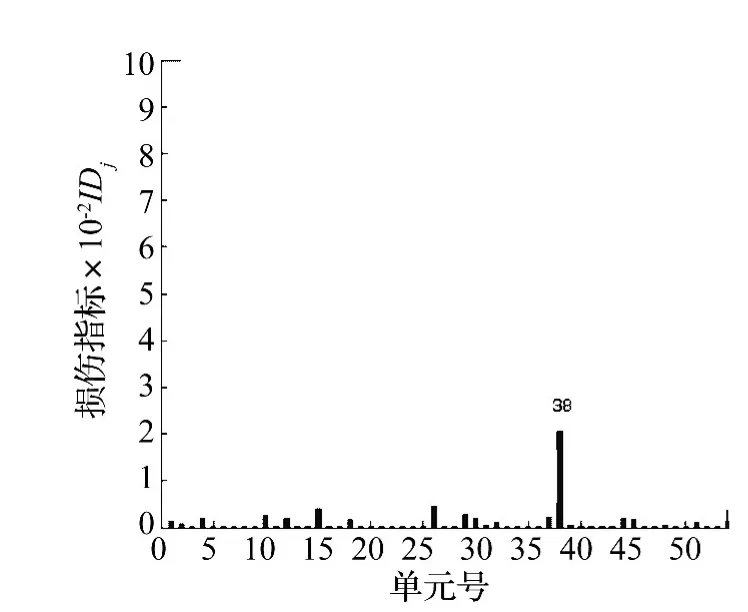
图4 单元38损伤20%时损伤诊断结果Fig.4 Crack results of injury 20%Unit 38

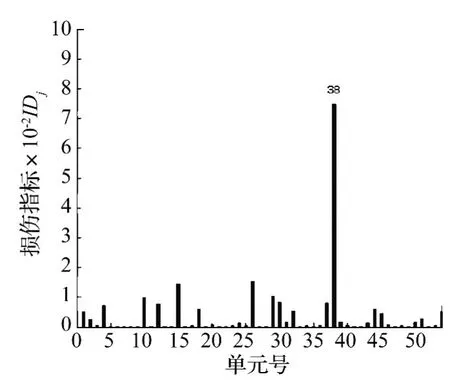
图5 单元38损伤50%时损伤诊断结果Fig.5 Crack results of injury 50%Unit 38

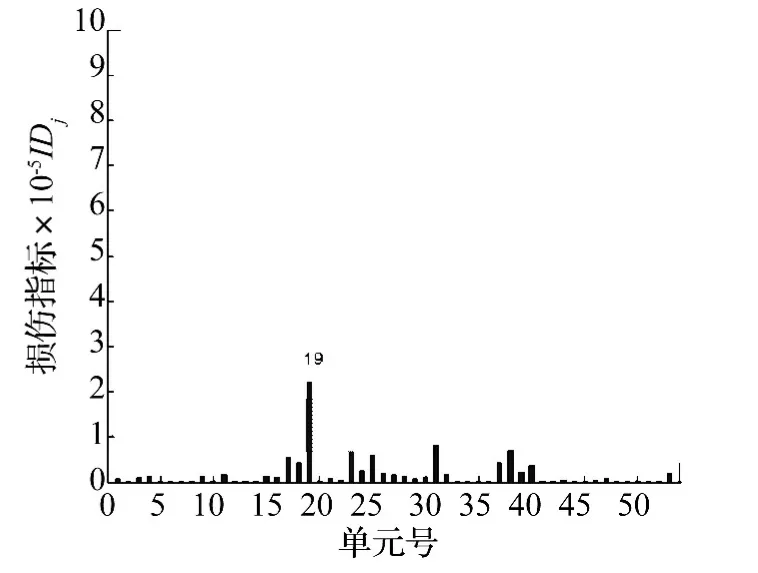
图6 单元19损伤20%时损伤诊断结果Fig.6 Crack results of injury 20%Unit 19

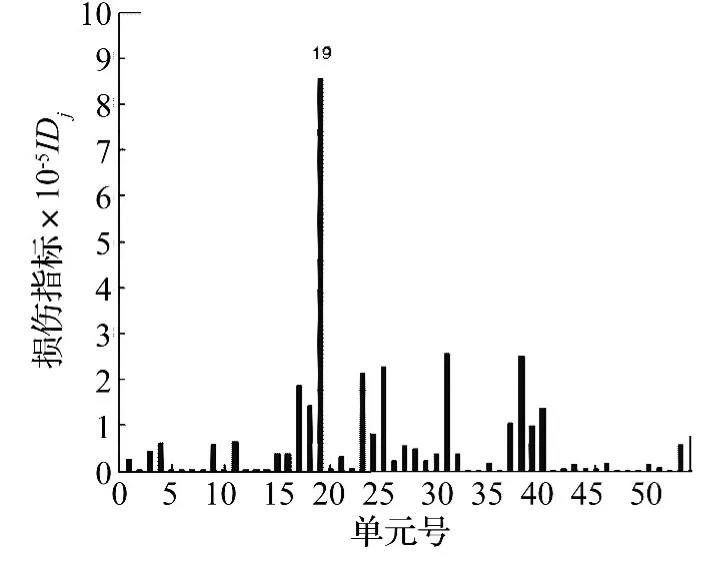
图7 单元19损伤50%时损伤诊断结果Fig.7 Crack results of injury 50%Unit 19

图8 单元23损伤20%时损伤诊断结果Fig.8 Crack results of injury 20%Unit 23

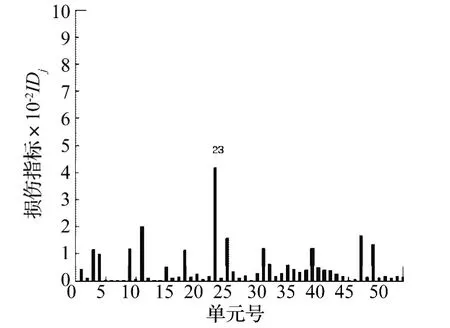
图9 单元23损伤50%时损伤诊断结果Fig.9 Crack results of injury 50%Unit 23

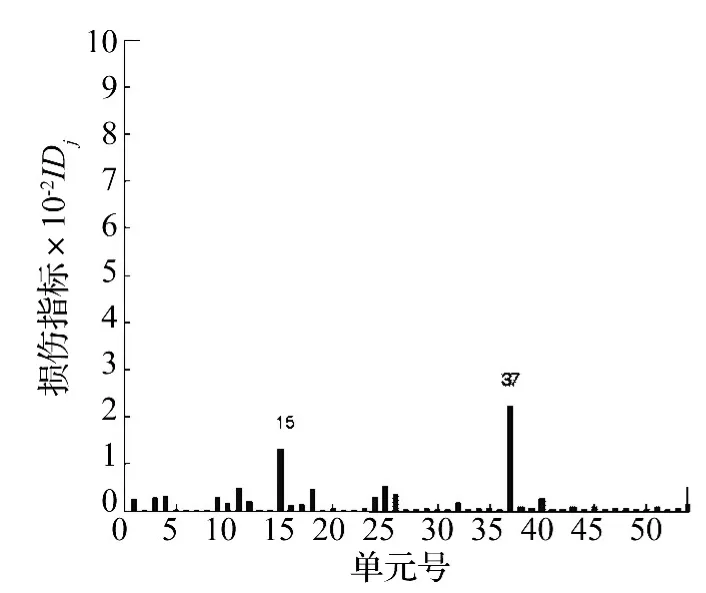
图10 单元15和单元37损伤20%时损伤定位结果Fig.10 Crack results of injury 20%Unit 15 and Unit 37

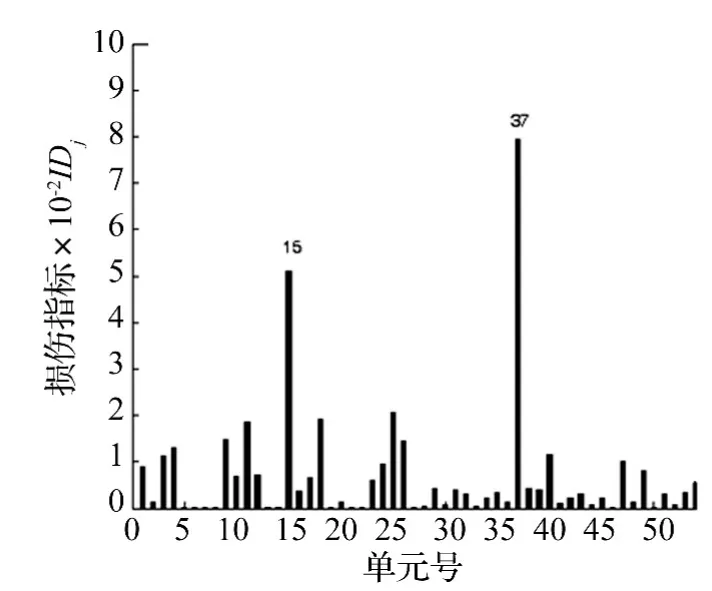
图11 单元15和单元37损伤50%时损伤定位结果Fig.11 Crack results of injury 50%Unit 15 and Unit 37

图12 单元25和单元38损伤20%时损伤定位结果Fig.12 Crack results of injury 20%Unit 25 and Unit 38

图13 单元25和单元38损伤50%时损伤定位结果Fig.13 Crack results of injury 50%Unit 25 and Unit 38

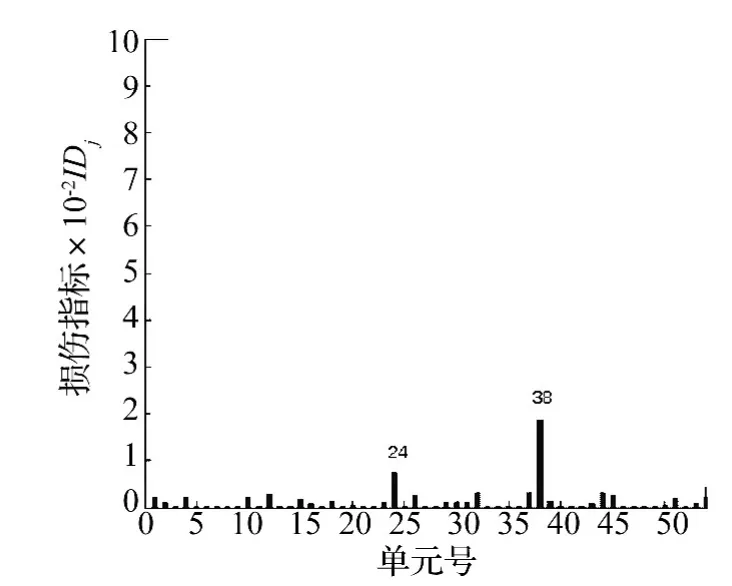
图14 单元24和单元38损伤20%时损伤定位结果Fig.14 Crack results of injury 20%Unit 24 and Unit 38

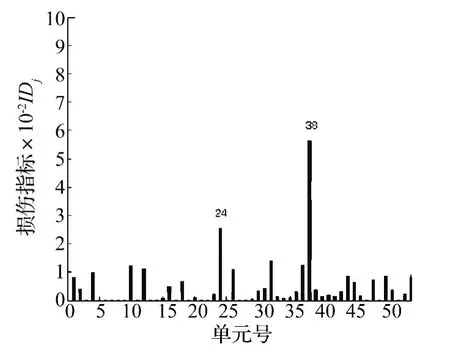
图15 单元24和单元38损伤50%时损伤定位结果Fig.15 Crack results of injury 50%Unit 24 and Unit 38

由图3、图4可知，当单元38发生损伤时，损伤构件处出现明显的峰值点，损伤指标IDj能正确进行损伤定位，未损伤单元的指标值在一个小量范围内，大小约为损伤单元指标值的1/5～1/4，可预先将此设定为判断是否损伤的阀值。随着损伤程度的加深，指标值增大，可以对损伤程度进行初步判断。图5至图14列出其他损伤工况定位结果。从图2中可以看出，单元23较单元19，单元39更靠近平台底部固定端，当单损伤工况时，单元23受损会对刚度矩阵造成更大的改变，从而对周边相关单元模态应变能产生更大改变，而出现部分指标大于1/5～1/4的现象。

从上述的数值模拟结果中可以看出，本文提出的损伤诊断指标能够正确的诊断出海洋平台结构的各类构件的不同损伤程度的工况。且与文献［8］中的方法比较，具有以下优点:不需进行两阶段法诊断，轴向模态应变能比法损伤指标明显，可直接用于损伤定位;综合利用损伤前后一、二阶模态，信息更加完备，结果更加可靠。

3 实验验证

通过模拟固定式导管架海洋平台的结构特点，制作了一个钢质平台物理模型，采用冲击荷载进行外部激励，对应传感器布置方案得到各节点的加速度响应信号，对采集到的结构加速度振动信号用标量型自回归滑动平均方法(ARMA)进行模态参数识别，使用识别出的结构损伤前后的低阶模态，研究本文提出的算法进行海洋平台结构损伤检测的可行性。

3.1 海洋平台结构模型的制作与安装

表3 模型构件截面尺寸Tab.3 Cross Section data of physical model component

钢质导管架平台实物模型见图16。材料特性及各构件截面尺寸见表3。考虑平台上部结构的特点，在模型顶部设置一厚20mm的钢板。对在实验中要损伤的构件，设置拼接法兰接头，拆开接头并抽出中间垫板，构件完全损伤，重新安装接头构件复原。平台物理模型制作好后，固定在混凝土基座上。

试验中采用美国SILICON DESIGNS公司电容式加速度传感器，德国Imc集成测控有限公司数据采集仪，北京东方振动与噪声技术研究所多功能抗混滤波放大器，江门市安泰电子公司数显倾角仪，在模型试验中采用了橡胶头力锤冲击激励。具体敲击方法是分别在Y向和X向敲击模型顶层钢板的中部。

图16 平台的实物模型Fig.16 Physical model of jacket platform

3.2 模型的损伤事件设计工况及损伤诊断结果

模型的损伤事件设计工况为:构件25单元完全断开。

假设各单元的损伤定位指标式(9)符合正态分布，那么将其标准化得到鲁棒性更好的损伤诊断指标为:

用标准化的损伤诊断指标式(10)对模型进行诊断，结果如图16所示。

图17 斜撑25单元发生损伤诊断结果Fig.17 Crack results of Unit 25

从以上的诊断结果可以看出，本文提出的基于轴向模态应变能比的损伤诊断指标能够成功的诊断出海洋平台结构构件的损伤工况，且不需要模型修正，不需要高阶模态信息及转动自由度的信息。故该方法有望应用于实际结构的损伤诊断。

4 结论

本文提出了一种适用于三维桁架结构损伤诊断的轴向模态应变能比法，该指标利用结构损伤前后的前两阶模态参数，无需利用高阶模态信息及结构转动自由度的测试信息判断结构的损伤情况。用一个导管架式海洋平台结构数值模型对本文提出的损伤诊断指标进行了验证，最后通过物理模型实验对该方法进一步进行了实验验证。结果表明，本文提出的损伤诊断指标可正确的进行结构损伤定位，具有较好的实用价值，有望应用于实际结构的损伤诊断。

［1］ Stubbs N，Kim J T，Topole K.An efficient and robust algorithm for damage localization in offshore platforms［C］.//In proc.ASCE Tenth Structures Congress，1992，543-546.

［2］杨和振，李华军，黄维平.基于振动测试的海洋平台结构无损检测［J］.振动工程学报，2003.16(4):480-484.

YANG He-zhen，LI Hua-jun，HUANG Wei-ping.Nondestructive damage detection in offshore platform structure using vibration monitoring［J］.Journal of Vibration Engineering，2003，16(4):480-484.

［3］张德文，魏阜旋(美).模型修正与破损诊断［M］.北京:科学出版社.

［4］ Stubbs N，Kim J T.Improved damage identification method based on modal information ［J］.Journal of Sound and Vibration ，2002，252(2):223-238.

［5］张兆德，王德禹.基于模态参数的海洋平台损伤检测［J］.振动与冲击，2004，23(3):5-10.

ZHANG Zhao-de ，WANG De-yu.Study on crack detection using modal parameters of a damaged jacket platform［J］.Journal of Vibration and Shock，2004，23(3):5-10.

［6］高维成，刘 伟，邹经湘.基于结构振动参数变化的损伤探测方法综述［J］.振动与冲击，2004，23(4):1-7.

GAO Wei-cheng， LIU Wei， ZOU Jing-xiang. Damage detection methosd based on changes of vibration parameters:a summary review［J］.Journal of Vibration and Shock，2004，23(4):1-7.

［7］ Hu S L J，Li H，Wang S.Cross-model cross-mode method for model updating［J］.Mechanical Systems and Signal Processing，2007，21:1690-1703.

［8］姜绍飞，张永强，吴兆旗.基于一阶振型的海洋平台二阶段损伤定位方法［J］.华中科技大学学报(城市科学版)，2008，25(3):31-34

JIANG Shao-fei，ZHANG Yong-qiang，WU Zhao-qi.A twodamage localization method based on the first mode shape of offshore platform structure［J］.J.of Hust.(Urban Science Edition)，2008，25(3):31-34.