基于振动能量回收的自供电MR阻尼器集成与试验研究

汪志昊，陈政清

(1.华北水利水电学院土木与交通学院，郑州 450011;2.湖南大学风工程试验研究中心，长沙 410082)

所谓能量回收，就是将一些常常直接消耗或废弃的能量通过某种方式转化为有用的能量。目前，这些研究主要集中在航天、机械与微电子领域，其振动特点是高频、微幅，可回收能量的功率在微瓦级，能量回收装置主要以压电材料为载体［1］。土木工程结构的振动也是一种能量，且从理论上讲，还是一种很大的能量。通过回收振动能量，有望解决结构振动主动、半主动控制的能量源问题，而能量源正是制约减振效果较好的结构主动与半主动控制技术工程实际应用的重要因素［2］。

孙作玉等［3］提出了一种不需要外部能源供给的主动控制方案，其原理是利用“换能器”将结构的一部分振动能量转换为液压能存储在蓄能器，并利用它作为主动控制的动力源。Nerves等［4］结合永磁无刷直流电机与调谐质量阻尼器(TMD)仿真分析了对某高层建筑结构风振、地震的混合控制，其中TMD充当电机与被控结构之间能量传递的中介。Scruggs等［5］提出了基于永磁无刷直流电机进行振动能量回收的主动质量阻尼器(AMD)，即利用回收的振动能量施加AMD所需的主动控制力;Scruggs等［6］还首次系统提出了基于结构振动能量回收的土木工程结构半主动或主动控制理论设想;Scruggs等［7］最近又成功研制了最大出力达1 kN的三相能量回收电机，推进了振动能量回收技术在土木工程中的潜在应用。

由于土木工程结构现有的振动能量回收技术效率较低，难以驱动主动控制装置，研究者就联想到将能量回收技术与需要较小能耗的磁流变(MR)阻尼器结合起来使用。Cho等［8］提出在传统的MR阻尼器的活塞杆上额外固定永磁体，在其周围同时设置感应线圈。当活塞杆运动时，感应线圈的磁通量发生变化而产生感应电动势，然后直接给MR阻尼器的励磁线圈供电，从而形成具有自供电特性的MR阻尼器。遗憾的是，Choi等［9］的振动台测试结果仅给出了在各种激励下感应线圈产生的电动势，却没有将MR阻尼器作为负载，测试在同源激励下MR阻尼器的出力。事实上，对于MR阻尼器这个用电器而言，虽然所需供电功率较低，正常工作仍需要两个必要条件，即足够的供给电压与输入功率。因此，该方案虽然概念清晰，充满前景，但事实上对于振动频率低、幅值小的土木工程结构，能量回收效率较低，再加上电路损耗，预计难以投入到实际结构振动控制中应用。与文献［8-9］的工作类似，Sapiński［10］提出采用图1所示的直线电机回收振动能量，然后供给低功耗的MR阻尼器。然而电机与MR阻尼器同处在10 mm振幅、1 Hz正弦激励下的测试结果表明:相对零电压输入，自供电MR阻尼器出力并没有发生明显的变化。Choi等［11］理论构思了图2所示的自供电MR阻尼器系统，其通过TMD子系统来放大固定在动子上的永磁体与感应线圈的相对速度，以期产生更大的电动势与输出功率。

图1 直线发电机Fig.1 A linear DC generator

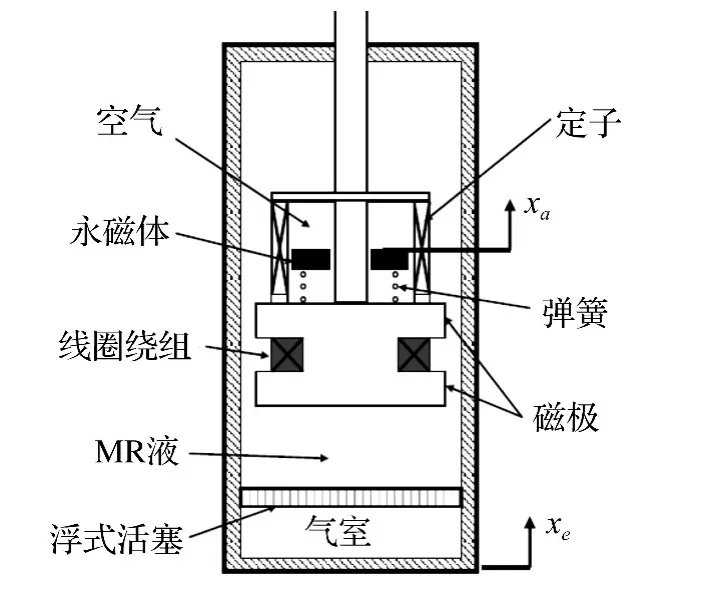
图2 结合TMD的自供电MR阻尼器Fig.2 A self-powered MR damper combining with a TMD

从以上的分析可以看出，目前的土木工程结构振动能量回收技术研究仍处于概念阶段，离实际应用还有相当大的距离。此外，在能量回收技术与MR阻尼器的集成研究中，多数研究者均还局限于采用能量回收效率较低的直线电机。Gupta等［12］通过试验对比了直线电机与旋转式电机在同等尺寸下的输出功率问题，发现直线电机比旋转式电机至少低21%。虽然将直线发电机用于土木结构的振动能量回收，原理清楚、概念清晰、装置简单，但其能量的回收效率低，且受行程的制约。针对以上不足，首先测试与分析了旋转式永磁电机的振动能量回收效果，接着构建了由永磁电机与MR阻尼器集成的自供电MR阻尼器减振系统，并测试了相应的电、力学性能，最后定性讨论了自供电MR阻尼器系统的减振机理。

1 旋转式发电机的选型与性能测试

1.1 基本性能

微型旋转式发电机的典型代表就是在自动控制中常用的测速发电机，它是一种测试机械转速的电磁装置，能把机械转速转化为与之成正比的电压信号。直流测速发电机的电枢电动势Ea可表示为:

式中:ke表示测速电机的电动势常数，n表示电机转子转速。忽略电枢接触压降，负载为RL时的输出电压为:

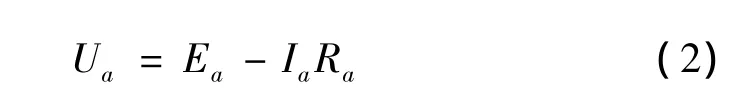
式中:Ra表示电枢内阻;Ia表示电枢电流，其计算式为:

把式(1)、(3)代入式(2)即可得到输出电压的计算式:

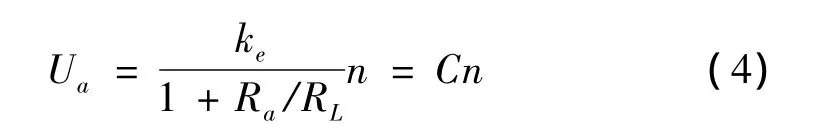
式中:C表示发电机输出特性的斜率，当Ra≪RL时，有C=ke。因此，发电机的总功率PT与输出功率PO分别为:

1.2 电机选型

用于土木工程结构振动能量回收的旋转式电机需要满足的要求有:① 磁场由永磁体激发，不需要外界电源励磁;② 在具有较大电动势常数ke的前提下，同时具有较小的内阻Ra与重量、尺寸。根据上述要求，本文中振动能量回收装置采用上海某电机公司生产的CFX-03型直流测速发电机，见图3所示。出厂主要性能参数有:电动势常数ke为0.06 V/(r·min-1);静态常温电阻6.4 Ω;重3.7 kg;最大设计转速3 000 r/min。

图3 旋转式永磁测速发电机Fig.3 A rotary permanent magnet tachogenerator

1.3 振动源为旋转运动的电机性能测试

为了评估测速发电机用于土木工程结构振动能量回收的可行性，首先通过变频电机带动测速发电机同速转动，测试发电机的电源电动势及在一定负载下的输出电压与功率，测试装置如图4所示。试验采用变频器改变交流电机的转速，电机的输出电压直接采用DH5920动态信号测试系统采集。

图4 发电机的输出电压与功率特性测试装置Fig.4 Experimental setup for measuring output voltage and power of a generator

图5给出了不同转速下发电机的电源电动势与15 Ω负载下的输出电压，由图可知，电源电动势、输出电压与转速均接近完全的线性关系。据此，可以拟合出发电机的电动势常数ke为0.059 4 Vmin/r(与出厂值几乎相等)，负载15 Ω发电机的输出特性斜率C为0.051 9 Vmin/r，此时对应的发电机输出功率与转速的关系见图6所示。

图5 断路与15 Ω负载的电机输出电压Fig.5 Output voltages with open circuit and 15 Ω resistor

图6 负载15 Ω时的电机输出功率Fig.6 Output power of the generator loaded with 15 Ω

1.4 振动源为直线运动的电机性能测试

当振动源为直线往复运动时，必须首先为能量回收电机设计直线-旋转传动装置，将振动源的直线运动转化为电机转子的转动。直线-旋转传动的常见形式有:齿条齿轮机构、链条链轮机构与精度更高的滚珠丝杠等。由于链条链轮最为简单，对导向的要求不严，且成本最低、耐久性高，试验最终选用这一方式传动。能量回收电机性能测试系统的原理示意图见图7所示，其由变频电机、变频器、偏心轮、测速电机、弹簧、链条链轮与激光位移计、东华数据采集系统构成。试验中，首先通过变频器调节变频电机的转速，变频电机转轴带动偏心轮转动，经过链条上的弹簧预拉力，使得链条往复直线运动，最后带动测速电机的转子正反方向的转动。试验采用了两种规格的偏心轮，对应的链条直线运动振幅分别为5 mm、10 mm;链轮的有效转动半径为 2.3 cm。

图7 能量回收电机性能测试系统示意图Fig.7 The diagram of experimental setup for performance testing of an energy harvesting motor

图8给出了直线激振位移幅值5 mm、频率2 Hz下的发电机电源电动势与负载为15 Ω时对应的输出电压时程曲线，由图可知，测速电机不但可以作为结构振动的能量回收装置，理论上还有望作为结构局部振动的速度传感器。图9给出了直线运动振幅分别为5 mm、10 mm，发电机的最大电源电动势与负载15 Ω的输出电压随振动频率的变化关系;图10给出了负载15 Ω时的最大输出功率随振动频率的变化关系。综合图9、10可以看出:在运动振幅一定的情况下，电源电动势、15 Ω负载下的输出电压均与振动频率成线性关系;即使在如此小的激励振幅下，测速电机仍有一定的功率输出，且随着激励振幅与频率的增加而迅速放大。图10还暗示出:对于振动频率低、幅值小的土木工程结构，采用微型电机回收得到的电功率也将会较小，导致能量回收具有一定的挑战。

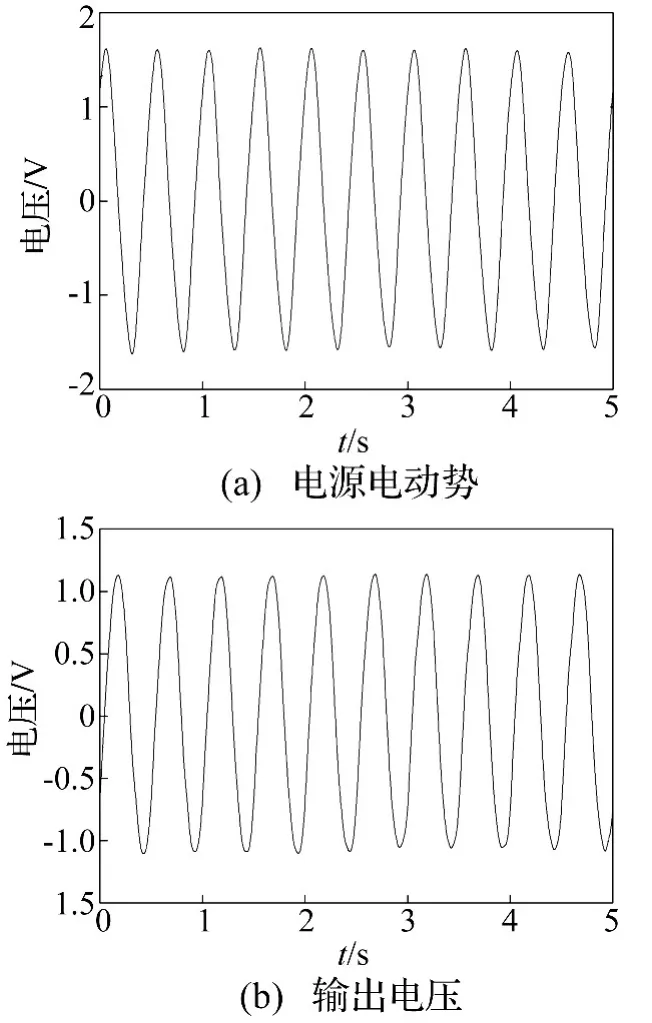
图8 发电机的电源电动势与输出电压时程曲线Fig.8 Time histories of electromotive force and output voltage of the generator

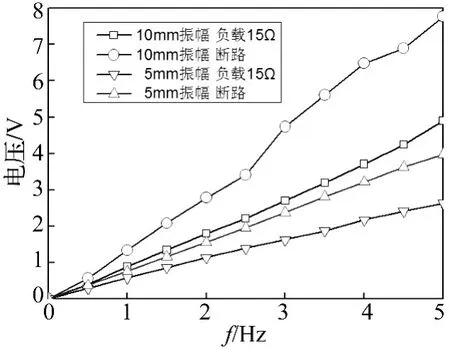
图9 各种工况下的电机最大输出电压Fig.9 Maximum output voltages of the generator in each case

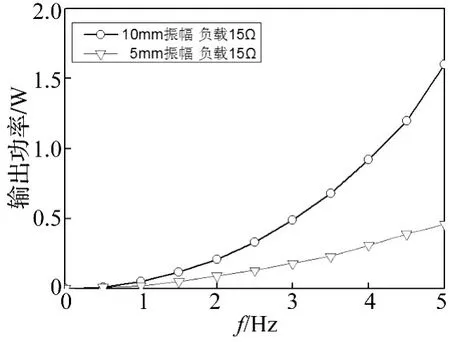
图10 各种工况下的电机最大瞬时输出功率Fig.10 Maximum output power of the generator in each case

2 自供电MR阻尼器系统构成及力学性能

2.1 自供电MR阻尼器系统构成

构建的自供电MR阻尼器智能减振系统框图见图11所示，该系统由电磁调节式MR阻尼器、直线与旋转运动转换机构、永磁旋转式发电机与控制器四部分组成，其中控制器为可选部分。该系统的突出特点有:永磁式直流发电机既是结构振动的传感器(可以通过发电机输出电压的大小和方向，测量结构振动的相对速度信息)，又是减振系统控制的能源发生器(为MR阻尼器提供电源);无需外界电源，就可实现MR阻尼器出力的调节;根据是否设置控制器，既可作为具有自适应特征的被动控制系统，也可实现半主动控制。半主动控制的控制器可由可变电阻器、二极管、继电器开关、电容器和单片机等组成。出于实际工程应用考虑，本文仅研究自供电MR阻尼器的被动控制。

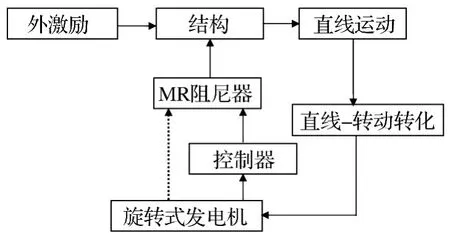
图11 基于振动能量回收的MR阻尼器智能减振系统Fig.11 The flow chart of a self-powered MR damper system based on vibrational energy harvesting

2.2 自供电MR阻尼器力学性能测试

试验采用美国LORD公司生产的RD-1005-3型MR阻尼器，其主要性能参数有:最大出力约为3 kN;行程为±2.5 cm;最大瞬时输入电压12 V;功耗小于10 W;励磁线圈常温下内阻为5Ω。测试中将MR阻尼器固定在激励试验台上，并接入发电机的回路，以实现MR阻尼器与带动发电机转动的链条线位移为同源激励的测试，测试原理与实验装置见图12所示。测试的主要参数有:能量回收电机的输出电压，即MR阻尼器的输入电压;MR阻尼器的出力。

图12 自供电MR阻尼器系统测试装置Fig.12 Experimental set-up for a self-powered MR damper system

图13给出了MR阻尼器出力随位移、速度及MR阻尼器输入电压的变化曲线，其中激振位移振幅为10 mm，激振频率依次为1、2、3、4和5 Hz。图14给出了3 Hz激振频率下，激振位移、MR阻尼器输入电压及阻尼力的时程。综合图13、14可知:① 电机回收的振动能量完全足以驱动MR阻尼器，且简谐激励时阻尼器的出力也呈简谐规律变化;② 自供电MR阻尼器体现出粘滞阻尼的性质，且自供电MR阻尼器的等效粘滞阻尼系数(即力与速度关系椭圆的长轴斜率)与阻尼器激振频率几乎无关;③ 在各个激振频率下，自供电MR阻尼器的最大出力既没有对应最大输入电压时刻，也没有对应最大的阻尼器速度，表明了MR阻尼器的速度与实际输入电压并不是理想的完全同相位，而是存在一定的相位差。

图13 MR阻尼器出力与位移、速度及输入电压的关系 (由内至外依次为1、2、3、4与5 Hz)Fig.13 Loops of MR damper force verse displacement，velocity and voltage(from inner to outer in order as 1-5 Hz)

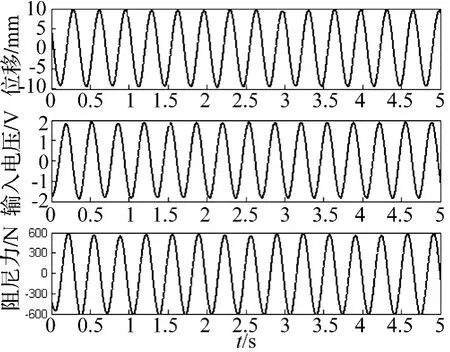
图14 激振位移、MR阻尼器的输入电压与阻尼力的时程Fig.14 Time histories of excitation displacement，voltage and damping force of the MR damper

计算得到MR阻尼器速度与输入电压二者之间的相位差随激振频率的变化关系见图15所示，由图可知:① 在各个激振频率下，相对阻尼器振动速度，MR阻尼器的输入电压均有不同程度的时延，这体现的正是能量回收电机的电感效应;② 相位差随激振频率的增大先逐渐增大，在3 Hz达到最大，然后开始逐渐下降;③ 根据相位差与对应的激振周期，可以计算得到1、2、3、4和5Hz激振时相对阻尼器速度，输入电压的时间延迟分别为 10.3、12.0、11.6、8.4 与 4.0 ms，可见低频(1～3 Hz)激振时产生的时间延迟基本相等。整体而言，发电机的电感效应在低频激振时影响较小。

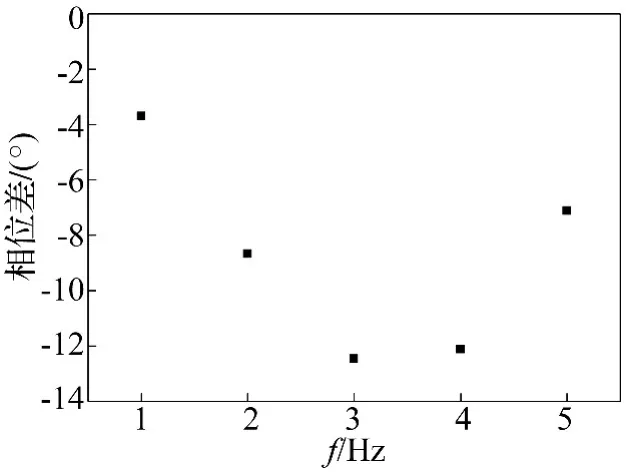
图15 自供电MR阻尼器输入电压与速度的相位差随激振频率的变化关系Fig.15 Phase lags between input voltages and velocities f the self powered MR damper versus vibration frequencies

3 自供电MR阻尼器被动控制的减振机理

虽然自供电MR阻尼器也可以设计为半主动控制系统，但本文仅探讨自供电MR阻尼器的被动控制，也就是将电机产生的电动势直接供电给MR阻尼器。虽然形式上是被动控制，但这里暗含两种重要的结构振动主动或半主动控制思想，分别是速度反馈与离复位控制，故称作自适应被动控制。速度反馈控制属于状态反馈控制的一种，即控制指令按照某种控制律通过结构振动的速度反馈。所谓离复位控制也称作经典的Bang-Bang控制［13］，简单实用，用于 MR阻尼器半主动控制时，阻尼器的输入电压切换规则可以表示为:

式中:v(t)，Vmax分别表示MR阻尼器的控制电压与最大容许输入电压;xm，x·m分别表示阻尼器的位移与速度，或受控结构观测点的位移与速度。式(7)表明离复位控制是一种基于控制装置或结构局部振动位移与速度方向的反馈控制:当位移与速度同向，此时阻尼器或结构远离平衡位置，则施加最大输入电压;反之，则输入零电压。但是，这种控制有一个主要缺点，即会导致结构穿越平衡位置时的速度过大［14］。

图16总结比较了MR阻尼器的最优被动控制、Bang-Bang控制与自供电控制策略对应的MR阻尼器输入电压示意图。从图中可以看出，自供电MR阻尼器的被动控制兼具离复位与速度反馈控制的特征。若MR阻尼器与能量回收机构安装在同一位置，即MR阻尼器与能量回收机构的链条线位移完全相等，由于MR阻尼器的电压控制输入与结构的振动速度成正比，自供电MR阻尼器的被动控制也就形成了天然的结构速度反馈控制。忽略发电机输出电压相对结构振动速度的时间延迟，则有:当速度最大，即结构在平衡位置，此时电机的输出电压最大，若直接输入到MR阻尼器，使MR阻尼器的可调阻尼力最大，恰好最大限度抑制结构离开平衡位置的运动;反之，结构振动速度为零，即位移最大，此时发电机的输出电压最小，使MR阻尼器的可调阻尼力最小。

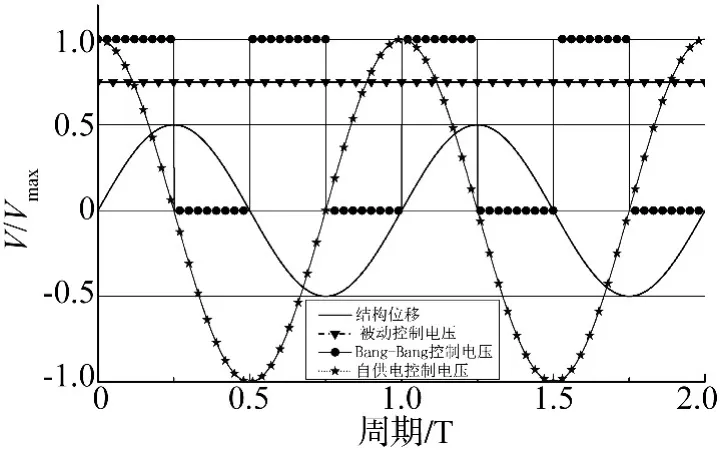
图16 基于MR阻尼器的各种控制策略示意图Fig.16 Various kinds of control strategies based on MR dampers

值得注意的是，自供电MR阻尼器被动控制的局限也是显而易见的:一方面由于速度反馈只是基于结构的局部振动速度信息，一般只能最优地控制结构的局部响应，不能保证对整个结构系统的最优控制;另一方面，如果能量回收电机的输出电压过大，导致MR阻尼器出力过大，可能会导致MR阻尼器的锁定，从而也就无法正常耗能减振。因此，基于自供电MR阻尼器的被动控制系统成功与否取决于两个重要因素:① 结构的局部速度传感是否能够完全或基本表征结构的全局振动信息，从基于状态空间的现代控制论来看，就是局部的传感器测试信息是否足以观测或估计结构的全部状态;② 能量回收电机的参数要预先根据被控结构的振动频率与幅值水平进行合理设计，以控制电机的最大输出电压，避免MR阻尼器呈现严重的嵌固效应或完全被锁定，甚至损坏MR阻尼器。

4 结论

为了摆脱基于MR阻尼器的振动控制系统对外界电源的依赖，本文提出了一种采用结构振动能量回收技术的自供电MR阻尼器减振系统，并进行了力学性能测试与减振机理的定性分析。主要结论有:

(1)采用旋转式永磁直流电机进行土木工程结构的振动能量回收是一种切实可行的技术与方法，相对通常采用的直线电机，旋转式电机具有能量回收效率高，且基本不受结构往复直线运动行程的限制;

(2)只要振动源的幅值与频率处于土木工程结构振动的常规水平，本文提出的结构振动能量回收技术就可以解决足尺结构振动控制用RD-1005型MR阻尼器对外置电源的依赖;

(3)当MR阻尼器与电机为同源激励时，自供电MR阻尼器的被动控制具有天然的速度反馈控制与离复位控制特性。因此，自供电MR阻尼器具有较好的工程应用前景。

［1］Priya S，Inman D J.Energy harvesting technologies［M］.New York:Springer，2009.

［2］陈政清，汪志昊.基于能量回收的土木工程结构振动控制［J］.建筑科学与工程学报，2009，26(2):9-14.

CHEN Zheng-qing， WANG Zhi-hao. Structural vibration control based on energy harvesting in civil engineering［J］.Journal of Architecture and Civil Engineering，2009，26(2):9-14.

［3］孙作玉，刘 季.结构振动控制的无能源主动控制［J］.地震工程与工程震动，1999，19(3):102-105.

SUN Zuo-yu， LIU Ji. Active structural vibration control without power supply［J］.Journal of Earthquake Engineering and Engineering Vibration，1999，19(3):102-105.

［4］Nerves A C，Krishnan R.A strategy for active control of tall civil structures using regenerative electric actuators［C］.Proceedings of 11th ASCE Engineering Mechanics Specialists Conference，Florida，1996，503-506.

［5］Scruggs J T，Lindner D.Active energy control in civil structures［C］.Proceedings of SPIE Conference on Smart systems for Bridges，Structures，and Highways，California，1999，3671:194-205.

［6］Scruggs J T，Iwan W D.Control of a civil structure using an electric machine with semi-active capability［J］.ASCE Journal of Structural Engineering，2003，129(7):951-959.

［7］Scruggs JT， Cassidy IL， BehrensS. Design and experimental characterization of a three-phase，1KN regenerative actuator［C］. Proceedings of5th World Conference on Structural Control and Monitoring，Tokyo，2010，038(1-10).

［8］Cho S W，Jung H J，Lee I W.Smart passive system based on magnetorheologicaldamper［J］. SmartMaterials and Structures，2005，14:707-714.

［9］Choi K M，Jung H J，Lee H J，et al.Feasibility study of an MR damper-based smart passive control system employing an electromagnetic induction device［J］.Smart Materials and Structures，2007，16:2323-2329.

［10］Sapiński B.An experimental electromagnetic induction device for a magnetorheological damper［J］.Journal of Theoretical and Applied Mechanics，2008，46(4):933-947.

［11］Choi Y T，Wereley N M.Self-powered magnetorheological dampers［J］.Journal of Vibration and Acoustics，2009，131:044501(1-5).

［12］Gupta A，Jendrzejczyk J A，Mulcahy T M，et al.Design of electromagnetic shock absorbers［J］.International Journal of Mechanics and Materials in Design，2006，3:285-291.

［13］禹见达，陈政清，王修勇，等.改进的Bang-Bang控制算法的理论与试验研究［J］.振动与冲击，2010，29(2):60-63.

YU Jian-da，CHEN Zheng-qing，WANG Xiu-yong，et al.Theoretical and experimental study on an improved Bang-Bang control algorithm［J］.Journal of Vibration and Shock，2010，29(2):60-63.

［14］杨润林，闫维明，周锡元，等.基于离复位控制策略的结构振动控制研究［J］.工程力学，2006，23(5):1-8.

YANG Run-lin，YAN Wei-ming，ZHOU Xi-yuan，et al.Study on vibration control of structures based on the off-andtowards-equilibrium control strategy［J］. Engineering Mechanics，2006，23(5):1-8.