高速凸轮NURBS廓线改进人工鱼群多目标动力学优化

玄冠涛，邵园园，吕钊钦，冯显英，郑继周

(1.山东农业大学 机械与电子工程学院，山东省园艺机械与装备重点实验室，泰安271018;2.山东大学 机械工程学院，济南250061)

随着生产发展的需要，高速凸轮机构在轻工、内燃机等自动、半自动机械中应用越来越广泛。凸轮转速越高，系统受到的振动和冲击越大，特别是从动件的残余振动会造成凸轮机构的定位精度变差和传动精度降低，因此必须对从动件的残余振动进行控制。Wiederrich［1］分析了多自由度凸轮机构残余振动准则，Chew等［2］通过控制从动件上有效的弹簧力实现凸轮机构的动态优化并提出了一种减少残余振动的直接方法，Yamada等［3］则利用反馈控制减少残余振动，Grewal等［4］对不同凸轮廓线下高速弹性凸轮机构的性能进行了分析和比较，孙树峰等［5-6］分析了凸轮 NURBS廓线、廓面的运动学性能，但并未深入研究动态特性。

本文采用非均匀有理B样条(Non-uniform rational B-Splines，NURBS)重构高速凸轮廓线，建立高速凸轮机构单自由度弹性动力学模型，基于改进的人工鱼群算法对NURBS廓线进行多目标动力学优化，保证凸轮良好运动性能的同时，最大限度的抑制振动和冲击。

1 高速凸轮廓线NURBS重构

一条k次NURBS曲线定义为:

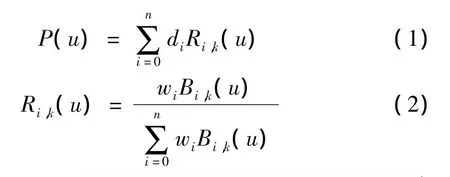
式中di(i=0，1，…，n)为控制顶点;wi(i=0，1，…，n)为权因子;Ri，k(u)为k次有理 B 样条，Bi，k(u)为由节点矢量U=［u0，u1，…，un+k+1］决定的k次 B 样条有理基函数。

高速凸轮廓线NURBS重构，就是利用廓线的采样点，根据式(1)、(2)反求出相应NURBS廓线的控制顶点及权因子，通过相关参量调整实现凸轮NURBS廓线优化。无量纲表示［7］的高速凸轮NURBS廓线的位移、速度、加速度和跃度表示为:

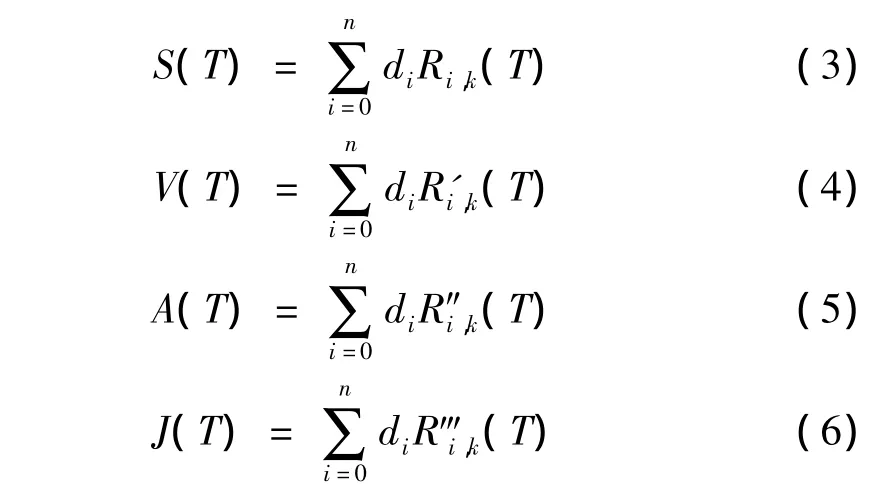
式中:(T)、(T)和(T)为k次有理B样条的1阶、2阶和3阶导数。若运动规律的加速度和跃度连续，理论上就不存在刚性和柔性冲击，对降低残余振动和提高定位精度很有利，因此须保证NURBS曲线的次数k≥3。同时为减小高速凸轮机构的最大速度Vm、最大加速度Am，还要取较低的次数，一般取3≤k≤5。

2 高速凸轮多目标动力学优化设计

2.1 弹性动力学模型

在高速凸轮机构中，受系统参量(质量、阻尼和刚度等)的影响，从动件实际运动规律与理论运动规律存在偏差，并伴有冲击、振动和噪声，须将凸轮机构看成一个弹性系统，建立图1单自由度弹性动力学模型，Koster［8］已证明该模型具有足够精度。

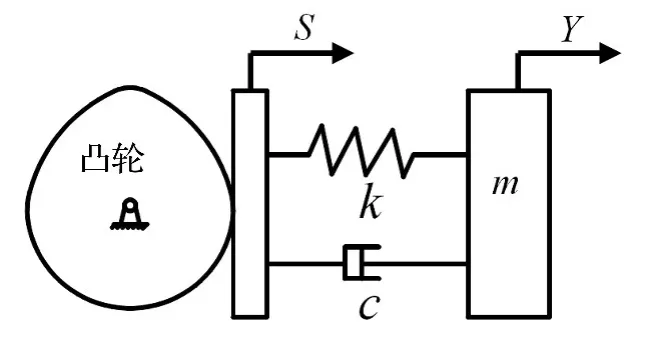
图1 单自由度弹性动力学模型Fig.1 Single degree of freedom dynamic model

图1中m为系统等效质量，k为系统等效刚度，c为系统的等效阻尼系数，S为无量纲理论位移，Y为无量纲实际位移。若凸轮廓线即理论位移为s，实际输出位移为y，则系统的运动微分方程为:

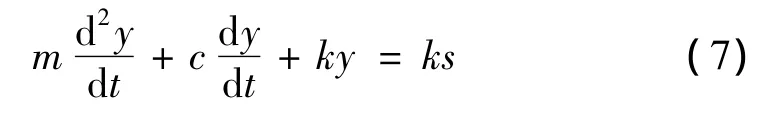
采用凸轮的无量纲表示

在升程阶段，系统在位移激励作用下做受迫振动，为主振动阶段。当凸轮机构结束升程(T＞1)，激励消失，系统进入余振阶段，由式(8)求得从动件输出位移的残余振动振幅Ar:

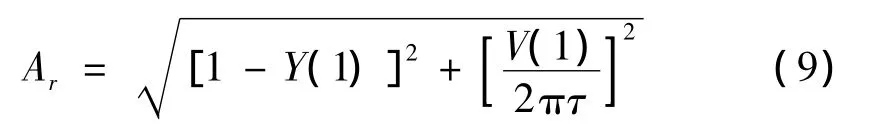
式中:Y(1)和V(1)是T=1时从动件的实际位移和速度。

2.2 多目标优化数学模型

凸轮廓线优化设计时一般以最大速度Vm、最大加速度Am等运动学参数为目标函数，而在高速凸轮机构中，残余振动的抑制成为首要考虑的问题。为此，以凸轮NURBS廓线的控制顶点di和权因子wi为设计变量，建立高速凸轮廓线多目标优化数学模型:

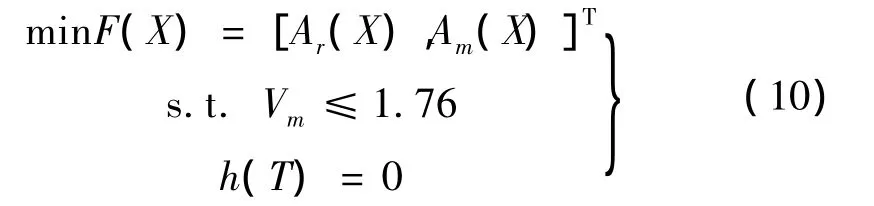
式(10)为了和修正正弦(Modified Sine，缩写为“MS”)廓线比较，将最大速度特性值限定为1.76作为不等式约束，h(T)=［S(0)，V(0)，A(0)，S(1)-1，V(1)，A(1)］T为满足表1应用较广泛的双停留工作方式边界条件的等式约束。

表1 D—R—D运动边界条件Tab.1 D—R—D kinematics boundary condition

在上述优化模型的设计中，要求运动学和动力学同时达到最优是不可能实现的，甚至是相互矛盾的，为保证凸轮机构良好的动力学性能，只能在其运动学性能不劣于传统廓线的情况下，最大限度的减少残余振动的影响，获得系统的Pareto最优解。

3 改进人工鱼群多目标优化算法

人工鱼群算法［9-10］(Artifical Fish Swarm Algorithm，AFSA)模仿自然界鱼群觅食、聚群、追尾行为，通过鱼群中各个体的局部寻优达到全局最优。该算法前期的收敛速度较快，但在算法的后期，鱼群的多样性变差，算法进化停滞不前，易陷入局部极值点，导致寻优结果精度低和运算速度慢。因此，本文利用改进的人工鱼群(Improved Artificial Fish Swarm Algorithm，简称IAFSA)多目标优化算法，采取禁忌搜索策略，以MS廓线的特性参数为参照，在理想的加速度和残余振动幅值的邻近区域，对高速凸轮机构多目标动力学模型进行变参数二次寻优，获得系统的Pareto最优解集。IAFSA算法流程如图2所示。

图2 改进的人工鱼群算法流程图Fig.2 Flow diagram of improved artificial fish swarm algorithm

3.1 人工鱼群初始化和参数定义

IAFSA多目标优化算法需要初始化一组鱼群，每条人工鱼个体状态定义为X=(d0，w0，d1，w1，...，dn，wn)，人工鱼的当前食物浓度为F(X)=［Ar(X)，Am(X)］T，N为鱼群数目，人工鱼间的距离li，j=‖Xj-Xi‖，人工鱼感知范围visual，人工鱼每次移动最大步长step，δ表示拥挤度因子，人工鱼觅食的最大试探次数Try_number。

3.2 禁忌搜索策略

禁忌搜索算法具有灵活的记忆功能，它通过局部邻域搜索机制和相应的禁忌准则来避免迂回搜索，利用特赦原则释放一些被禁忌的解域，并通过终止规则实现全局优化搜索。AFSA的禁忌搜索规则定义如下:

(1)禁忌准则:设人工鱼的当前状态为Xi，邻近伙伴数目Nf及中心位置Xc，若Yc＜Yi且NfYc＞ δYi，表明伙伴中心位置状态较优但已拥挤，则此邻域中存在非劣解，将Xi邻域移入禁忌表禁忌。

(2)特赦原则:若禁忌表中存在非劣解域，则将此解域特赦。

(3)终止规则:迭代次数G已到最大迭代次数Gm或者一定G内禁忌表不变，算法终止。

3.3 变参数二次寻优

为加快搜索速度，在算法前期进行一次AFSA寻优，设置算法的参数P1:visual、step、δ及N取较大值，Try_number较小，并利用禁忌准则锁定非劣最优解的邻域，同时将不存在非劣最优解的可行解域禁忌，避免二次寻优的盲目性。算法后期，在一次寻优的解域内二次AFSA寻优，参数设置P2:visual、step、δ及N取较小值，Try_number较大，以提高寻优精度，最后将放入公告板的Pareto最优解输出。

4 优化仿真与实验

4.1 优化仿真

在常见的凸轮机构从动件运动规律曲线中，MS曲线的Vm、Am较小，适合高速工况下，但动态特性较差。现用5次NURBS曲线重构凸轮MS廓线，取n=20，理想加速度和残余振动振幅为F*=［5.53 10-4］。IAFSA多目标优化算法的设置如下:人工鱼的数量N=100，禁忌表长度100，最大迭代次数Gm=500。一次寻优的参数P1:visual=6，step=1.5，δ=3，Try_number=1，二次寻优的参数P2:visual=0.5 ，step=0.2，δ=1，Try_number=3。设高速凸轮机构的 ξ=0.035，τ=10，用改进人工鱼群算法优化两个目标函数，求得部分Pareto最优解如表2所示。从表2可以看出，高速凸轮机构的运动学参数Vm、Am和残余振幅Ar是相互矛盾的，一般情况下很难使它们同时达到最优，决策者可根据凸轮机构的工作需要选择适合的Pareto最优解。其中，第3组解的残余振动较小适合于高速凸轮机构的工作要求，而运动学特性与MS曲线相差不大，因此利用该组解重构NURBS凸轮曲线。由动力学方程式(8)，求得凸轮机构从动件在推程期的主振动响应(位移、速度、加速度和跃度)曲线如图3～图6所示。

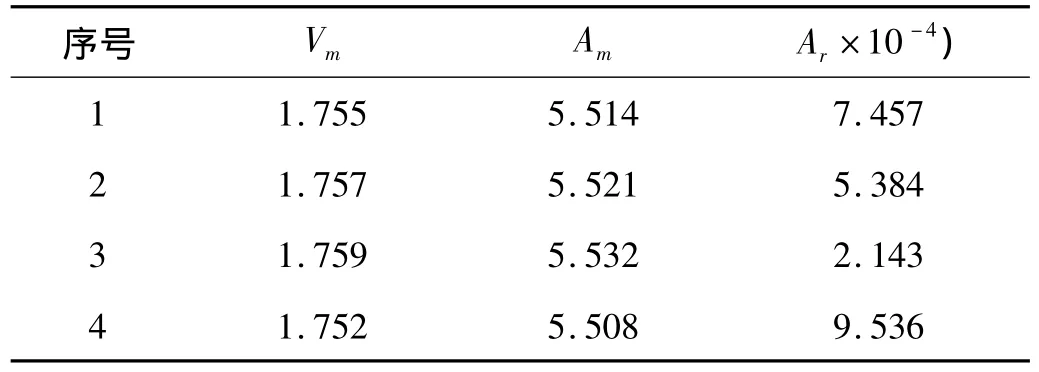
表2 IAFSA多目标优化的Pareto最优解Tab.2 Pareto optimal solutions based on IAFSA

从图3～6可以看出，优化后NURBS廓线的位移、速度和加速度响应同MS曲线相差不大，跃度曲线变化较平稳，最大跃度值较小，提高了系统工作的平稳性。

当T＞1，从动件到达推程终点，凸轮机构进入停歇期，由式(9)求解从动件余振响应，得τ=10时残余振动幅值响应曲线(图7)和不同周期比的残余振动幅值曲线(图8)。

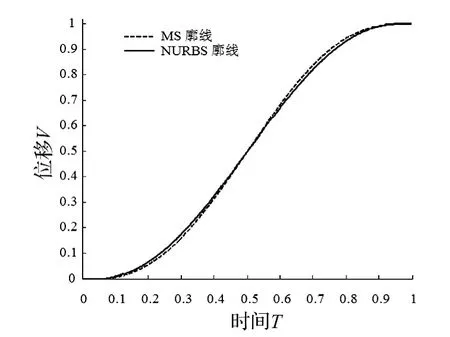
图3 位移响应曲线Fig.3 Displacement response curve

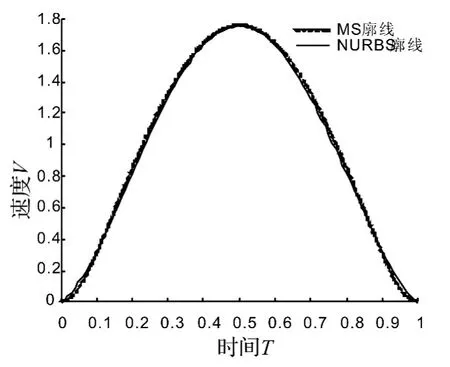
图4 速度响应曲线Fig.4 Velocity response curve

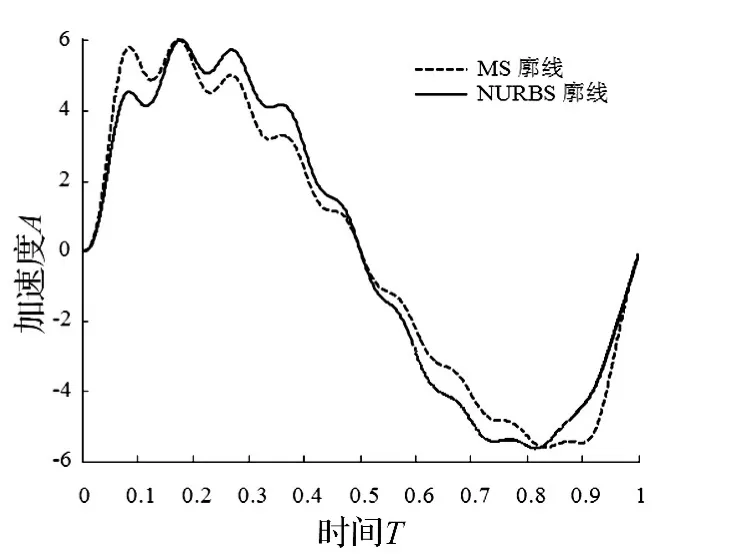
图5 加速度响应曲线Fig.5 Acceleration response curve

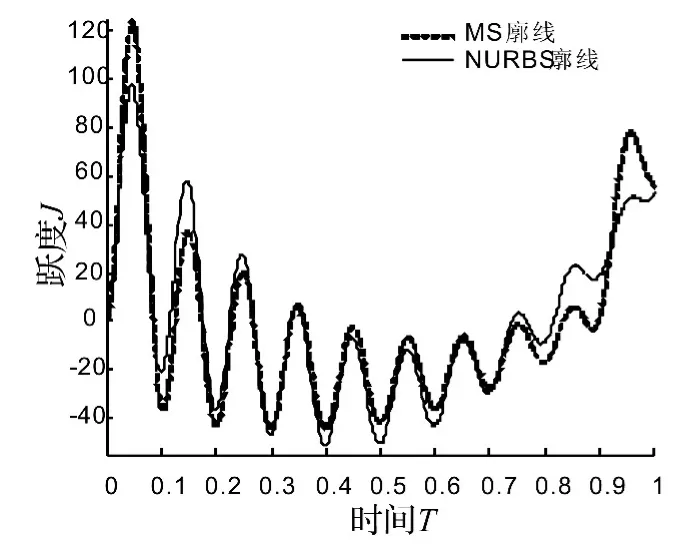
图6 跃度响应曲线Fig.6 Jerk response curve

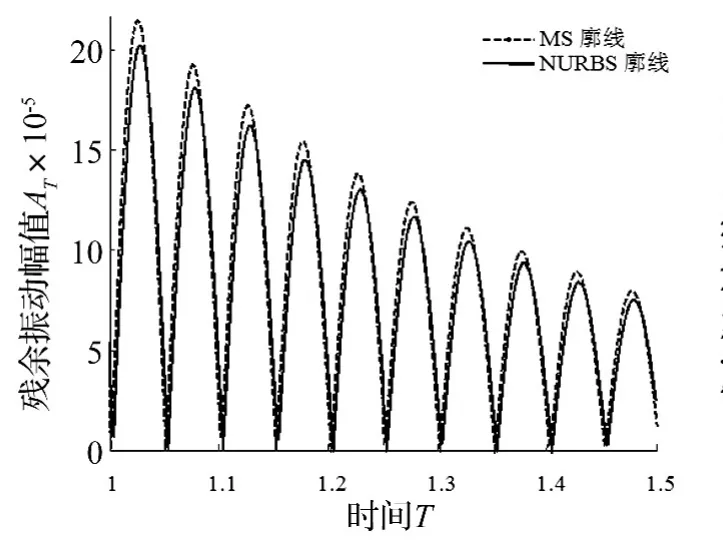
图7 残余振动幅值响应曲线Fig.7 Residual vibration amplitude response

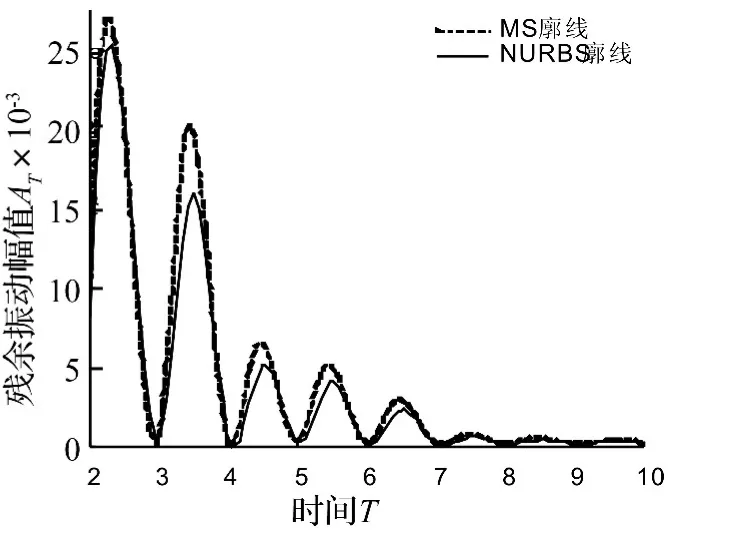
图8 不同周期比的残余振动幅值Fig.8 Residual vibration amplitude of different period ratio τ

图7表明，与MS廓线相比，优化后NURBS廓线的残余振动较小，残余振动的最大幅值降低了7.16℅，同时从图8可以看出不同的周期比时凸轮机构的残余振动也有不同程度的降低，周期比小时下降更为明显。

4.2 噪声实验

为进一步验证仿真结果，将MS廓线空间弧面分度凸轮机构和NURBS廓线空间弧面分度凸轮机构在不同转速下的噪声进行了实验测试，测试结果如表3所示。

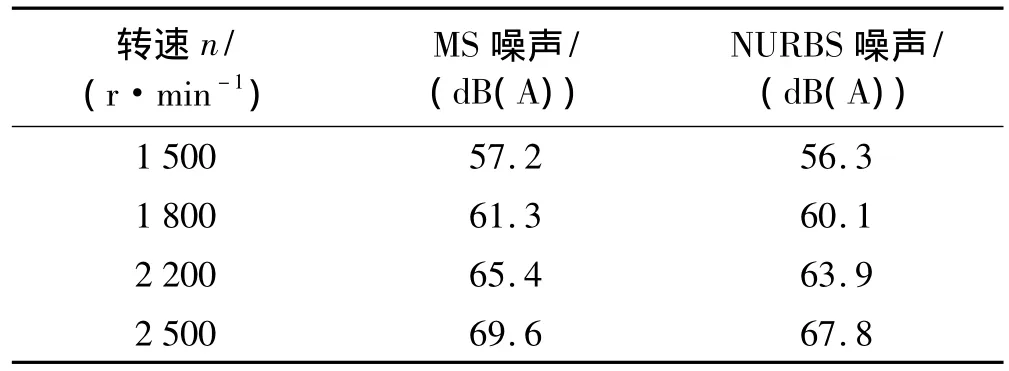
表3 不同转速的噪声(背景噪声23.2 dB(A))Tab.3 Noise of different rotate speed

分析表3中两种廓线下凸轮机构噪声的测试结果，可以看出NURBS廓线空间凸轮机构的噪声较小，高速时更为明显，这说明NURBS廓线凸轮的动力响应较好，冲击和振动的水平更低。

5 结论

本文基于单自由度弹性动力学理论，设计了高速凸轮机构多目标动力学优化模型，利用改进人工鱼群算法求解该模型，由获得的系统Pareto最优解重构高速凸轮 NURBS廓线，分析和比较了高速凸轮机构NURBS和修正正弦两种廓线的主振动和余振响应。结果表明:优化后高速凸轮NURBS廓线运动学性能不劣于修正正弦曲线，但降低了高速凸轮机构的残余振动幅值，提高了高速凸轮机构的动力学性能，减少了振动和冲击的噪声。

［1］Wiederrich J L.Residual vibration criteria applied to multiple degree of freedom cam-followers.Mechanical Design，1981，103:702-705.

［2］ Chew M，Chuang C H.Minimization residual vibration sin high-speed cam-follower system over a range of speed［J］.Mechanical Design，1995，117:l66-172.

［3］Yamada I，Nakagawa M.Reduction of residual vibrations in positioning control mechanism［J］.Journal of Vibration，Acoustics，Stress and Reliability in Design，1985，107:47-52.

［4］ Grewal P S，Newcombe W R.A comparative study of cam motion for high-speed sem-rigid follower cam systems［J］.Transaction of the CSME，1988，12(3):121-128.

［5］孙树峰，周以齐.基于非均匀有理B样条的空间凸轮设计［J］.机械工程学报，2009，45(8):125-129.

SUN Shu-feng，ZHOU Yi-qi.Design of spatial cam based on non-uniform rationalB-splines［J］.ChineseJournalof Mechanical Engineering，2009，45(8):125-129.

［6］玄冠涛，邵园园，吕钊钦，等.基于NURBS的空间分度凸轮廓面重构与仿真［J］.农业机械学报，2012，43(6):226-229，234.

XUAN Guan-tao，SHAO yuan-yuan，LÜ Zhao-qin，et al.Profile reconstruction of spatial indexing cam and simulation based on NURBS［J］.Transactions of the Chinese Society for Agricultural Machinery，2012，43(6):226-229，234.

［7］牧野洋.自动机械机构学［M］.北京:科学出版社，1980.

［8］ Koster M P.Vibration of cam mechanisms［M］.London:Mecmillan Press，1974.

［9］李晓磊.一种新型的智能优化方法—人工鱼群算法［D］.杭州:浙江大学，2003.

［10］李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式:鱼群算法［J］.系统工程理论与实践，2002，22(11):32-38.

LI Xiao-lei，SHAO Zhi-jiang，QIAN Ji-xin.An optimizing method based on autonomous animals:fish-swarm algorithm［J］.Systems Engineering Theory ＆ Practice，2002，22(11):32-38.