基于模态综合和移频方法的中频段模态计算

李兴泉，邓兆祥，李英强，章竟成，王腾腾

(1.重庆大学机械传动国家重点实验室，重庆 400030;2.汽车噪声振动和安全技术国家重点实验室，重庆 400039;3.重庆长安铃木汽车有限公司，重庆 401321)

固定界面模态综合方法将复杂结构划分为若干个子结构，采用各子结构的静力模态和低阶主模态对该子结构进行降阶变换，再将各子结构降阶矩阵综合成系统降阶动力学方程，即可求解系统低阶动态特性［1-2］。相对于传统有限元方法，模态综合方法仅保留少数低阶子结构主模［3］，因此，其构建的系统动力学方程阶数较低，更适用于复杂结构的低频动态特性计算。但对于划分成多个子结构的复杂结构来说，其界面自由度多，这影响了系统动力学方程的求解效率。为了进一步降低界面自由度的数量，部分文献采用特征约束模态进行界面自由度降阶，即基于特征约束模态降阶的模态综合方法［4-6］该方法减少了系统方程中的界面自由度数，提高了模态综合方法计算效率。但在实际的结构设计问题中，常常只需要计算某频段处的振动特性。文献［3］研究表明，各子结构的低阶主模态对较高频率的系统模态有重要影响，这说明即使只需要计算系统中频段模态，也要保留各子结构的低阶主模态，这使中频段模态的计算效率不高。在传统有限元方法计算系统中频模态时，可以采用移频方法来提高结构振动特性的计算效率［7-8］。SHYU 等［9-10］采用该移频方法来计算静力模态，提出了准静力模态方法，该准静力模态考虑结构惯性质量的影响，提高了模态综合的求解精度，但文中仍然采用原来的子结构主模态，这导致经过坐标变换后的子结构刚度矩阵不解耦，影响了模态综合的计算效率。文献［3］在此基础上采用移频后的刚度矩阵计算子结构主模态，这使坐标变换后的子结构刚度矩阵实现了解耦，文中还研究表明:采用移频方法后，子结构的低阶主模态对系统中频段模态的影响较小，因此低阶的主模态可以截断，这提高了系统中频模态的计算效率。但在复杂结构的中频段振动特性计算中，界面自由度多，此时系统界面自由度对应的特征约束模态的截断问题也显得相当重要，如何减少特征约束模态的数量，以进一步提高复杂结构中频段振动特性的计算效率，未见相关文献报道。本文推导了低阶特征约束模态对系统中频模态的影响，并采用移频技术来解决了低阶特征约束模态的截断问题，提高了模态综合方法对复杂结构中频段特性计算的效率。

1 特征约束模态降阶的模态综合方法

本文是研究采用特征约束模态降阶的模态综合方法计算复杂结构中频段模态时，低阶特征约束模态的截断问题，因此，首先对该模态综合方法进行简单介绍。

基于特征约束模态降阶的模态综合方法，是在固定界面模态综合方法的基础上，对系统质量和刚度矩阵中界面自由度对应的部分进行特征分解及降阶变换，再由降阶后的界面矩阵组集成系统降阶动力学方程，从而求解系统低阶振动特性。假设固定界面模态综合方法计算的广义坐标下无阻尼系统动力学方程为［1-2］:

式中:下标O和T分别为所有主模态对应的自由度标号和界面自由度标号，MOO、KOO分别为所有子结构主模态对应的系统降阶质量矩阵和刚度矩阵，MTT、KTT分别为所有界面自由度对应的系统界面质量矩阵和刚度矩阵，Q表示系统模态坐标。

由于各子结构只取少数低阶主模态，这使主模态对应的矩阵MOO和KOO的维数远小于所有子结构的内部自由度之和，则式(1)所示的降阶系统动力学方程的维数远小于有限元模型的自由度数，系统低频振动特性计算更容易，这是模态综合方法更适合于复杂结构振动特性计算的原因。

但在式(1)中，系统界面质量矩阵MTT和刚度矩阵KTT的维数仍然等于结构的界面自由度，对于划分成多个子结构的复杂结构来说，界面自由度多，界面质量和刚度矩阵的维数仍然较大，这影响了由式(1)计算系统低频振动特性的计算效率。

针对系统界面矩阵维数较大的问题，文献［4］等提出了采用特征约束模态来对系统界面矩阵进行降阶的方法，以提高模态综合的计算效率。该方法的基本原理为:界面质量矩阵MTT和刚度矩阵KTT是将结构的内部自由度静力聚缩到界面自由度上的矩阵。对于结构的低频特性计算问题，可以只取表征结构中低频振动特性的模态来对质量和刚度矩阵进行降阶，以减小振动特性的计算量。为此，先对式(1)中的界面矩阵进行特征分解:

式中，λc为特征值，Θc称为特征约束模态［4］，取前m阶特征约束模态Θcm(m＜T)，并对界面矩阵进行降阶坐标变换:

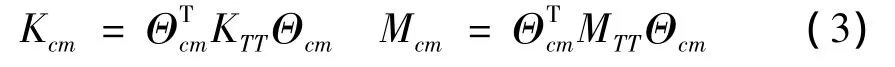
式中变换后，Kcm和Mcm都是m维的方阵，远小于界面自由度数T。对式(1)中矩阵副对角元素进行相应变换，即可重新构成系统降阶动力学方程:

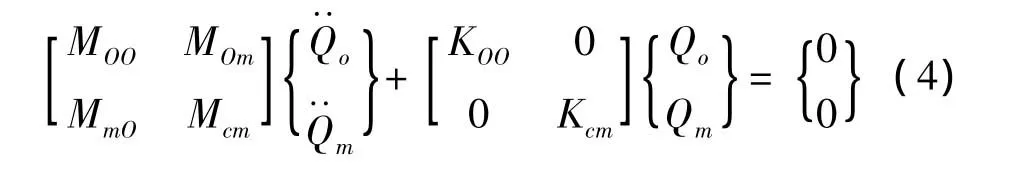
求解该方程并进行振型回代，即可得到系统中低频模态频率，这就是基于特征约束模态降阶的模态综合方法。相对于式(1)，式(4)所示的系统动力学方程的界面对应的自由度大为减小，提高了复杂结构低频动态特性计算的效率。

2 低阶特征约束模态的影响

在复杂结构的振动设计中，通常只关心某一中频段的振动特性。采用基于特征约束模态降阶的模态综合方法计算中频段模态时，保留了所有的中低频主模态和特征约束模态，这影响了复杂结构中频段模态的计算效率。文献［3］研究了子结构的低阶主模态对系统中频模态有重要影响，并采用了移频技术来对低频主模态进行截断。但对于特征约束模态与系统中频段模态的关系，以及低阶特征约束模态的截断问题未见相关报道，下面将对这些问题展开研究。

首先研究基于特征约束模态降阶的模态综合方法中，低阶特征约束模态对中频段模态的影响。为此，将式(3)中所选取的特征约束模态Θcm分为需要保留的特征约束模态Θcma和准备截掉的模态Θcmb两部分。由这两部分特征约束模态重新进行变换，则变换后式(4)所示的系统降阶方程可以重新写为:

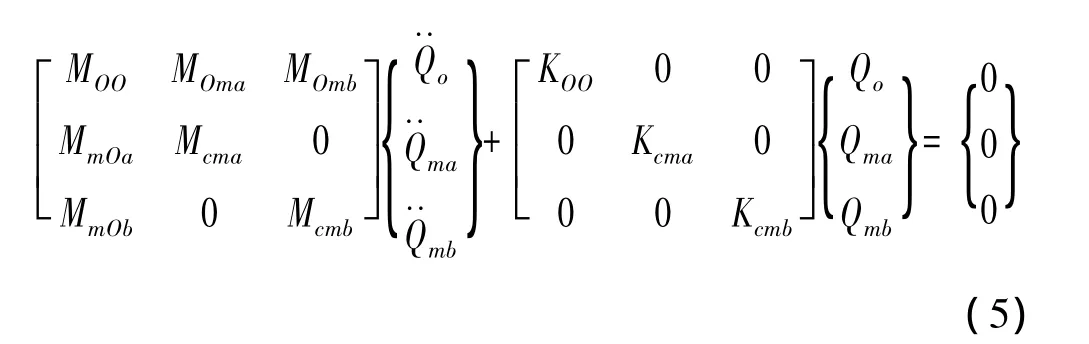
式中，Mcma、Mcmb分别为特征约束模态Θcma和Θcmb对应系统降阶界面质量矩阵，系统界面刚度矩阵的相应部分的意义相同。对上式的第三行展开，则模态坐标Qmb可表示为:

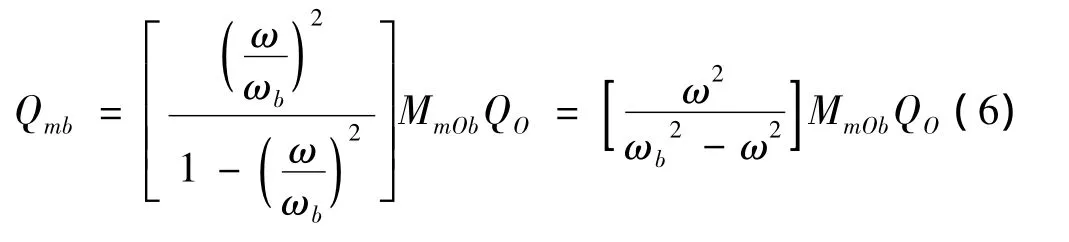
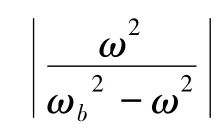
以上分析表明，当需要计算系统中频段模态时，低阶特征约束模态不能够截断，这使采用基于特征约束模态降阶的模态综合方法计算复杂结构中频段模态时计算效率不高。

3 移频及低阶特征约束模态截断

在传统有限元方法计算系统中频模态时，可以采用移频方法来提高结构振动特性的计算效率［7-8］。SHYU等［9-10］将该移频方法应用到了固定界面模态综合方法上，提出了准静力模态方法，但子结构矩阵坐标变换时仍然采用移频前的主模态，这使变换后的刚度矩阵不解耦，系统特性计算效率仍然不够高。文献［3］进一步采用移频后的刚度矩阵计算了子结构主模态，并对低阶主模态进行截断。但在复杂结构的中频段振动特性计算中，界面自由度多，此时系统界面自由度对应的特征约束模态的截断问题也显得相当重要，如何减少特征约束模态的数量，以进一步提高复杂结构中频段振动特性的计算效率，未见相关文献报道。下面将采用移频方法，对低阶特征约束模态的截断问题进行研究。

假设需要计算结构某中频段内的模态，该频段内系统本身的圆频率为ω，该频段的中心圆频率为ω0。根据传统有限元计算中移频方法的基本思想，对子结构的无阻尼自由振动微分方程进行移频处理:

式中:x表示子结构物理坐标，k和m为子结构物理坐标下的刚度和质量矩阵。为移频后的系统模态圆频率，其表达式为:

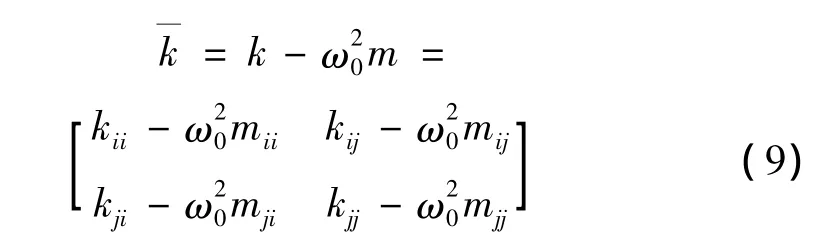
式中，下标i和j分别为内部自由度和界面自由度标号，mii为子结构所有内部自由度对应的质量矩阵，其它矩阵的意义类似。

移频之后，子结构的静力模态变为:

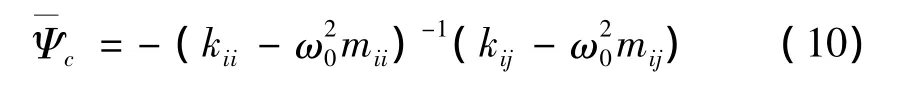
准静力模态中考虑惯性质量的影响，提高了系统模态的计算精度。但在子结构坐标转换过程中如果仍然采用移频前的主模态，将会使坐标转换后的子结构刚度矩阵不解耦，这将影响系统模态的计算量［9］。因此，需要对子结构刚度矩阵和质量矩阵中的内部自由度对应的部分重新计算主模态，即求解如下特征方程。

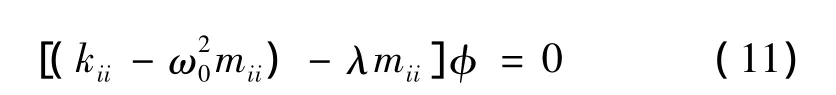
式中:λ为子结构主模态的特征值，φ为子结构主模态。取子结构的前k阶主模态构成向量矩阵:

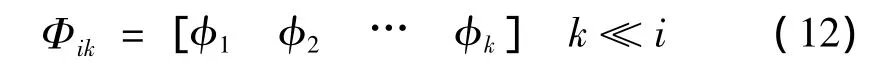
由移频后的子结构主模态和准静力模态，即可构成子结构的坐标转换矩阵为:

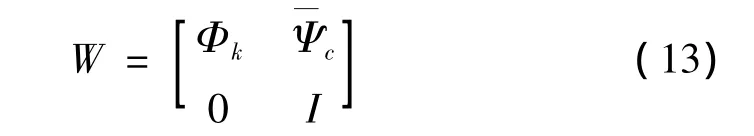
由该移频后的坐标变换矩阵，就可以对子结构的质量和刚度矩阵进行变换，如对刚度矩阵的变换过程为:

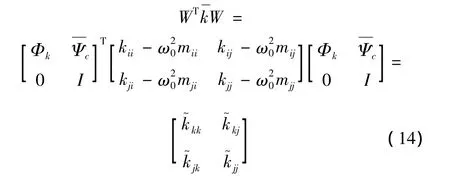
式中，转换后的刚度矩阵的对角元素的表达式为:

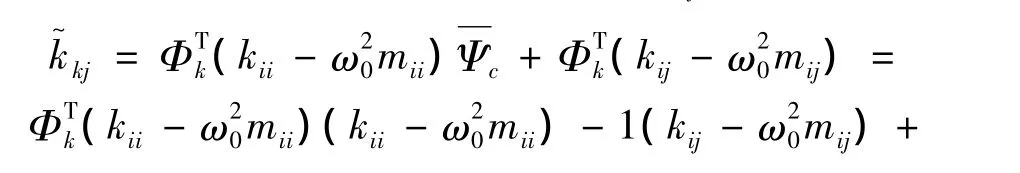
式(15)表明，移频后的子结构刚度矩阵经过坐标变换后，对角元素为0，即刚度矩阵实现了解耦，这使后面模态综合的计算效率较高。

由各子结构的坐标变换后的质量和刚度矩阵，按基于特征约束模态降阶的模态综合方法构建系统降阶动力学方程。则(5)式所示的系统动力学方程可以重新表示为:

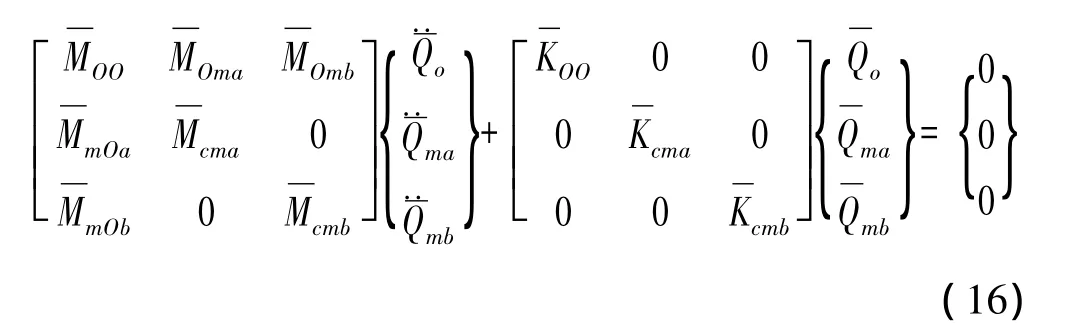
式(16)中，同样将前m阶特征约束模态对应的系统界面自由度分为保留的部分a和准备截掉的部分b，以研究移频后各特征约束模态的贡献。

将式(16)的第三行展开，并将式(17)代入，则式(6)可重新写为:

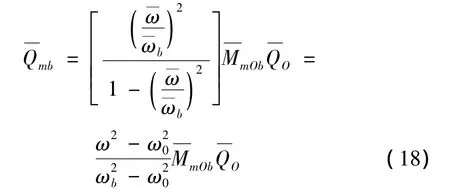
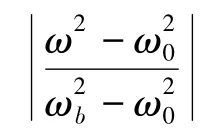
以上推导表明，对于复杂结构的中频段模态计算问题，采用移频技术后，低阶特征约束模态都可以截断，需要保留的高阶特征约束模态也更少。相对于不采用移频方法，参与计算的特征约束模态数减小，提高了模态综合方法对中频段问题的计算效率。

4 算法验证

图1所示的白车身有限元模型中，采用网格尺寸为20 mm的壳单元来建立个板件有限元模型，并采用梁单元来模拟焊点。共有201 231个节点，138 032个单元，其中包括117 539个四边形单元，14 951个三角形单元和5 542个梁单元。各板件的厚度及材料参数均由厂家提供。

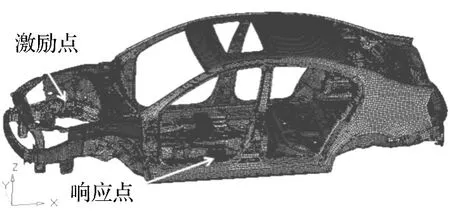
图1 白车身有限元模型Fig.1 Prototype vehicle mode

在车身上发动机右安装点处施加一单位激励，频率为0～400 Hz，采用基于特征约束模态降阶的模态综合方法计算车身0～400 Hz频率范围内的模态，并采用模态叠加法计算了驾驶员座椅处地板上的振动加速度。在160～190 Hz的中频段上，该点Z方向的振动加速度响应曲线有明显的峰值。本文采用移频方法，来计算该中频段内的结构响应特性，以验证移频方法对提高复杂结构中频段振动响应特性计算效率的有效性。在计算过程中采用NASTRAN软件的DMAP语言编写求解序列，并在一台双核2G内存的计算机上进行计算。

在160～190 Hz的中频段上，其中心频率为ω0=175 Hz。以该中心频率对子结构动力学方程进行移频处理，并对移频后的子结构主模态和特征约束模态进行截断。表1列出了是否采用移频方法时，特征约束模态、子结构主模态和系统模态截断的频率及保留的模态数。

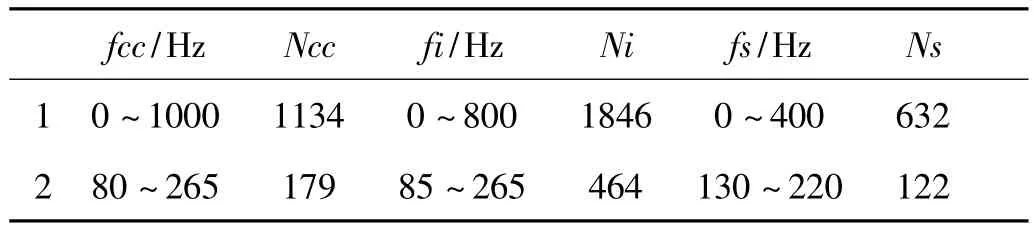
表1 模态频率范围及阶数对比Tab.1 Modal frequency range and modal numbers comparison

表1中，fcc、fi、fs分别表示特征约束模态、主模态和系统模态保留的频率范围，Ncc、Ni、Ns表示各模态在其频率范围内保留的模态阶数。

在表1中，第一行表示未采用移频方法的基于特征约束模态降阶的模态综合方法的计算结果。按照模态叠加方法的原理，要计算最高频率到190 Hz的响应加速度，需要2倍以上的系统模态来进行叠加，因此取系统模态为400 Hz。在基于特征约束模态降阶的模态综合方法中，需要保留系统最高计算频率的2倍频率范围内的主模态和2.5倍频率范围内的特征约束模态［5］，因此保留了子结构0～800 Hz以内的主模态和0～1 000 Hz以内的系统模态。

表1的第二行表示采用移频方法后的计算结果。在采用移频方法计算的各阶模态中，相当于考虑了关心频段的中心频率175 Hz处的惯性质量的影响，因此，可以取较窄频段内的模态来进行振动响应的计算。文献［3］中推荐保留关心频段宽度的2倍频带范围内的主模态来进行模态综合计算。本文需要计算160～190 Hz频段范围内的振动响应，则保留该频带宽度的2倍频段内的系统模态，即保留130～220 Hz范围内的系统模态;相应地，取2倍系统模态频段宽度，即85～265Hz内的子结构主模态和特征约束模态来进行振动特性的计算。

由表1可见，采用移频方法后的计算结果中(第二行)，需要保留的特征约束模态频率范围fcc，由移频前的0～100 Hz减小到80～270 Hz，保留的特征约束模态数Ncc由1134阶减少到了179阶。说明采用移频方法后实现了低阶特征约束模态的截断，也保留了更少的高阶模态数，这与移频方法的理论推导结果一致。同时，采用移频方法后，保留的子结构主模态频率范围fi和系统模态频率范围fs，以及它们对应的模态数Ni和Ns，也都相应地减小。说明采用移频方法后，提高了模态综合方法的计算效率。

采用移频方法后，驾驶员座椅处地板上的振动加速度响应如图2所示。

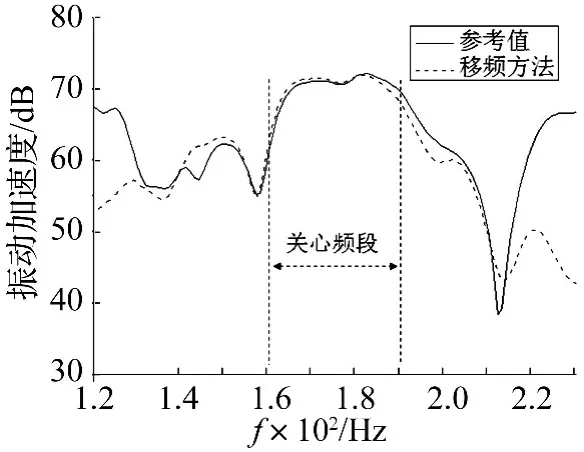
图2 振动加速度响应对比Fig.2 acceleration computation error comparison

在图2中，实线为基于特征约束模态降阶的模态综合方法计算的加速度响应，虚线为采用移频方法后的模态综合方法的加速度响应。由图可见，在160～190 Hz的关心频段范围内，振动加速度响应具有较高的计算精度，离中心频率175 Hz越远，响应的计算精度逐渐变差。

在中频段振动特性的计算时间上，采用基于特征约束模态降阶的模态综合方法计算时需要44分钟，采用移频方法后仅需要24分钟。这是因为采用移频方法后，由于保留的特征约束模态、子结构主模态和系统模态的频率带宽度都较窄(如表1中第二行所示)，这减小了系统动力学方程的维数，提高结构中频段振动响应的计算效率。

由以上分析可见，在基于特征约束模态降阶的模态综合方法的基础上，采用移频方法对系统中频段振动响应进行计算时，在保证较好的计算精度的同时，减小了计算时间，说明本文采用的移频方法计算复杂结构中频段模态时具有较高的计算效率。

5 结论

在复杂结构的中频段模态计算时，理论推导表明:传统的模态综合方法的低阶特征约束模态对系统中频模态有影响，不能截断;采用移频方法后，低阶特征约束模态和子结构主模态的低频部分都能截断。该方法对白车身有限元模型的中频段振动特性的计算结果表明:采用移频方法后，有效减少了需要保留的特征约束模态和子结构主模态的阶数，缩短了计算时间。说明本文所采用的移频方法提高了复杂结构中频段振动特性计算的效率。

［1］殷学纲，陈 淮，蹇开林.结构振动分析的子结构方法［M］.北京:中国铁道出版社，1991，9.

［2］Bampton M，Craig R.Coupling of substructures for dynamic analysis［J］.AIAA Journal，1968 ，6(7):1313-1319.

［3］ Zhang G，Component-based and parametric reduced-order modeling methods for vibration analysis of complex structures［D］. Mechanical Engineering. The University of Michigan，2005.

［4］姜忻良，王 菲.基于势能判据的约束模态综合法截断准则［J］.振动与冲击，2011，30(2)32-38.

JIANG Xin-liang， WANG Fei. Mode cut-off criterion of constrained mode synthesis method based on a potential energy criterion［J］.Journal of Vibration and Shock，2011，30(2)32-38.

［5］ Simon D M，Cost T L.Selection of characteristic constraint modes for component mode synthesis using a modification of effective interface mass［C］//46th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics and Materials Conference. Austin:American Inst. Aeronautics and Astronautics Inc.，2005:6564-6583.

［6］Castanier M P，Tan Y C，Pierre C.Characteristic constraint modes for component mode synthesis［J］.2001，39(6):

［7］张安平，陈国平.一种新的有限元模型移频动力缩聚法［J］.计算力学学报，2011，28(2):168-172.

ZHANG An-ping，CHEN Guo-ping.A noveldynamic condensation method with shift for finite element models［J］.Chinese Journal of Computational Mechanics，2011，28(2):168-172.

［8］Zhao Q C，Chen P，Peng W B.Accelerated subspace iteration with aggressive shift［J］.Computers and Structures，2007，85:1562-1578.

［9］Shyu W H，Ma Z D，Hulbert G M.A new component mode synthesis method:quasi-static mode compensation［J］.Finite Elements in Analysis and Design，1997，24:271-281.

［10］Shyu W H，Gu J M，Hulbert G M.On the use of multiple quasi-static mode compensation sets for component mode synthesis of complex structures［J］.Finite Elements in Analysis and Design 2000，35:119-140.