超声声表面波检测信号时差的倒频谱分析
2013-09-10闫晓玲董世运徐滨士王望龙
闫晓玲,董世运,徐滨士,刘 彬,王望龙
(1.北京理工大学 机械与车辆学院,北京 100081;2.装甲兵工程学院 装备再制造技术国防科技重点实验室,北京 100072)
激光熔覆再制造技术已应用于各工业领域装备机械构件修复,解决了许多再制造难题。但实践表明,激光熔覆涂层中的残余应力是影响其再制造机械零部件性能的关键因素之一。利用超声波可以直接对激光熔覆涂层进行应力的无损检测,从而为激光熔覆制备工艺优化提供指导,提高再制造构件的服役安全性。
利用超声波检测材料内部或表层应力的理论基础是声弹效应,即在应力作用下材料中的传播声速会发生变化。激光熔覆属于材料热加工过程,它以高能激光束作为移动热源。加工过程中,熔池周围的材料被快速加热,局部熔化,在随后的冷却、凝固过程中,必然会受到周围区域的约束,从而产生拉应力。根据成形基体的翘曲变形可以判断:熔覆层的残余应力以拉应力为主,沿着熔覆层厚度方向,拉应力逐渐减小。因此对于激光熔覆再制造产品,工程技术人员更关心的表层应力的分布状态。瑞利波是沿着固体表面传播的波,可用来检测熔覆层残余应力。
利用表面波检测材料表层应力的理论和实验研究[1-2],国内外的相关报道逐渐增多。如 Husson等[3]研究了在一定声程内表面波速度的变化和应力之间的关系。Duquennoy等[4-5]从弹性波理论出发研究建立了表面波传播相位变化与应力的线性关系,但实验研究还不够。在超声表面波应力检测技术中,由于应力引起的速度变化很微弱,100MPa应力导致的速度变化约为 0.1%(铝)和0.001%(钢)[6],因此时间差的精确读取是超声无损检测方法的关键技术。在信号处理中求时差的方法,一般通过求两个信号之间的互相关系数,由最大极值点来确定时差。但是实际检测过程中,超声声表面波信号要受到噪声的干扰,因此相关函数包含除时差以外的其它信息,这些信息必然会影响求时差的精确度。采用信号消噪方法可以抑制噪声,但是也丢失了一部分有用的信息,相关函数通过检测回波的最大峰值来确定时差,当最大峰值比较小时,经过滤波(消噪)后实际上不可能加以检测。文中提出基于复数倒频谱的超声声表面波时间延迟估计算法,采用该算法对模拟信号和实际检测信号做了时间延迟分析,并与相关法的分析结果做了对比,从理论上分析了复数倒频谱分析方法优于相关系数法的原因。
1 超声声表面波时差倒频谱分析基本原理
图1为表面超声波检测激光熔覆层残余应力的实验系统组成,表面波探头发射的信号s(n),透过耦合剂(机油)和试件的界面,在激光覆层中传播一定距离后,再次透过耦合剂和试样的界面,被接收探头接收。设s1(n)、s2(n)分别为无应力和有应力状态下的表面波回波信号,由于接收到的信号s1(n)、s2(n)波形相似,在时域上有延迟,忽略干扰情况下,它们之间的关系可表示为:
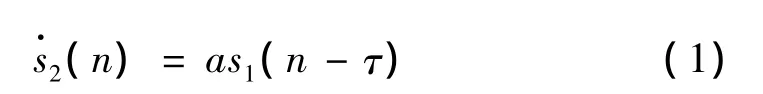
式中,a表示信号幅值的衰减,0<a≤1,τ为信号之间的时延。

图1 实验系统组成Fig.1 Experimental system components
倒频谱分析也称二次频谱分析技术,是现代信号处理科学中的一项新技术。它可以提供FFT频谱图上难以捕捉的信息,对于FFT频谱无法分辨的信息,倒频谱往往还能显示出延时峰。倒频谱分析包括功率倒谱分析和复倒谱分析两种主要形式[7],本文采用复数倒谱分析检测表面波声时差。
复数倒谱分析的定义为“信号序列傅里叶变换的对数傅里叶逆变换”,其表达式为

式中:cs(τ)为复数倒频谱,单位为dB;F-1表示傅里叶逆变换;自变量τ称为倒频率,具有时间量纲。
由于复数倒谱分析是对频域信号做对数转换(即转换成分贝)后再进行傅里叶逆变换,因此可以将频域信号之间的相乘(除),转变为时域信号的相加(减)。采用复数倒频谱方法检测表面超声波信号之间的延时,首先将信号s1(n)、s2(n)进行相加:
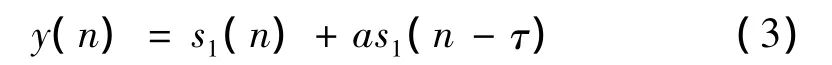
对式(3)两边取傅里叶变换:
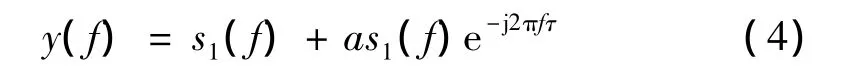
对式(4)两边取对数:
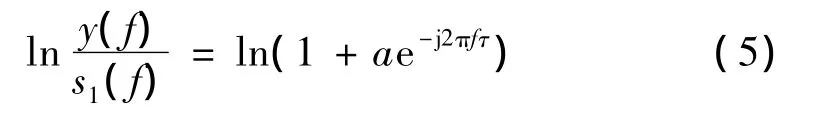
因为|de-j2πfτ|小于 1,所以 ln(1+ae-j2πfτ)可展成幂级数,所以有:

对式(6)两边取傅里叶逆变换,得复数倒频谱函数:
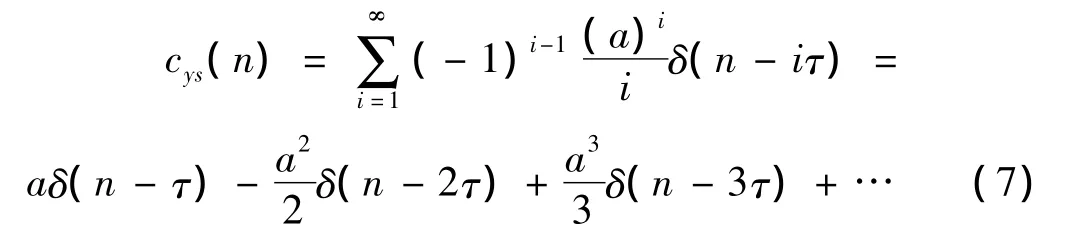
由式(7)可知,函数的倒频谱上,n=iτ(i=1,2,3)处会出现一系列δ脉冲,所以可以在复数倒频谱上分辨出延时峰。
2 倒频谱分析方法的实现和应用
图2为matlab7.0模拟的汉宁窗调制的频率为2.5 GHz,周期为7的正弦信号 S1、S2,信号之间的时差为500个采样点。图3(a)为倒频谱分析的结果,从图中可以清楚地看到在n=500i(i=1,2,3…)处出现了一系列δ脉冲。图3(b)为相关函数分析结果,从图中可以看出信号时差以极值方式(n=500)隐含在相关函数中,因此两种方法都可以辨别出时差信息,但是倒频谱分析的时延峰更尖锐,便于精确定位;另外模拟信号没有考虑噪声的影响,实际检测信号要受到噪声的干扰,相关函数包含了除时延以外的其它信息(声源信号以及各种噪声信息等),由式(7)可知复数倒频谱分析结果不受声源信号的影响,通过对信号在频域进行求和、求商运算,可以消除很大一部分噪声。下面结合超声声表面波检测信号的特点,分析倒频谱分析方法检测超声声表面波时差具有更高精确度的原因。

图2 模拟信号时域图Fig.2 Time-domain map of simulation signal

图3 信号时延分析结果对比Fig.3 Contrast of signal delay analysis result
(1)从表面超声波检测信号的特点进行分析。图1所示的超声检测系统,在适当的假设条件下,系统中各个组成部分都可以模拟成一个线性非时变系统[8-9],如图4所示,每个线性非时变系统的属性都分别由时域中的单位冲击响应函数(上侧)和频域中单位冲击响应函数的频谱(下侧)来表征。通过这一系列的线性非时变系统,用来激发超声波的电压信号就会转化为最终在示波屏上显示的带有有用信息的电压输出信号。
可见,由脉冲发生器产生的输入电压信号si(t)经过一系列信号转化过程,最终得到超声探伤仪示波器上显示的输出电压信号s0(t)。这个过程在时域中可表示为:

上述过程的频域表达式为:
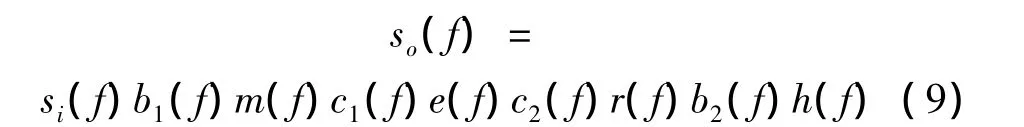
因此,最终超声探伤仪示波器上显示的输出电压信号,包含除了输入电压信号、被测试样信息之外其它不相关系统的影响。这些影响就是超声波检测信号中的噪声,可分为声学噪声和非声学噪声[10]。声学噪声主要是材料噪声,它来源于介质内部不同声阻抗界面上的反射、折射和散射,反映的是介质的微观结构。材料噪声静止的,相关的,扫描过程中,若换能器不动,不同次采样中的材料噪声相似。非声学噪声主要包括点电噪声、脉冲噪声和振铃噪声,这些噪声源于仪器电路中的随机扰动,换能器的震荡、仪器本身的波动等。
设s1(n)、s2(n)为接收探头接收到的表面超声波离散信号,s2(n)=as1(n-τ)
则:
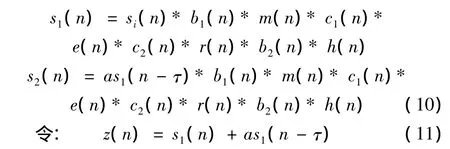
对式(11)做傅里叶变换:
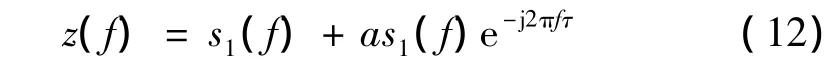
则:

从式(13)可以看出,采用本文所述的倒频谱分析方法求时差,上述表达式中不会出现声源信号si(n)的频谱,其它不相关系统与声源信号si(n)的卷积干扰(材料噪声、振铃噪声等)也被滤除,因此分析结果具有较高的信噪比。

图4 一系列线性非时变系统组成的NDE系统Fig.4 A series of linear time-invariant system consisting of NDE system
相关法求时差,主要从统计学分析角度对信号进行处理。设接收探头接收到的表面超声波离散信号s1(n)、s2(n)可表示为:

式中:s(n)(有用信号)为零均值高斯分布的平稳随机过程,s(n-τ)为s(n)延迟τ得到的零均值高斯分布的平稳随机过程,N1(n)、N2(n)(噪声)为为零均值高斯分布,可能互相相关的平稳随机过程。s1(n)、s2(n)的相关系数为:
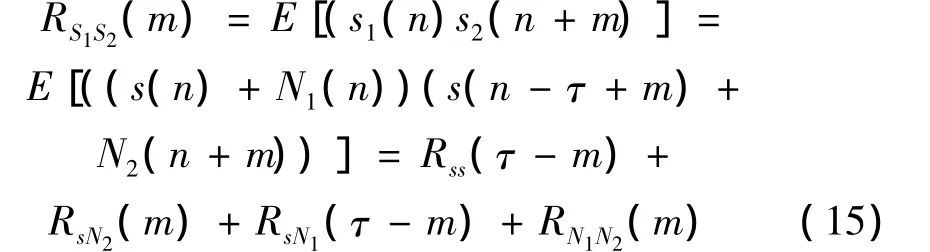
若信号和噪声,噪声与噪声之间互不相关(相关系数为0),则式(15)变为:
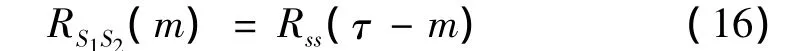
从式(16)可以得出,当m=0 时,Rs1、s2(0)=Rss(τ),因此相关系数取得最大值时的时间τ=(m-N)*T(T为信号采样周期,N为信号采样长度)即为表面波的传播时间差。
由上述分析可知,采用相关法求时差的前提条件是假定信号和噪声、噪声与噪声之间完全正交,但是表面超声波检测信号并不满足这样的假设条件,比如前面曾经分析过的材料散射噪声、超声波在换能器内部的反射引起的振铃噪声等,这些噪声都是相关的。因此这种情况下,采用关法求时差必然会影响求解的精确度。
(2)从倒频谱分析的特点分析。倒频谱实际上是频域信号取对数的傅里叶逆变换再处理,取对数的目的是为了使再变换后信号的能量更加集中。对信号做倒频谱分析,给信号频谱中的低幅值分量有较高的加权,可以帮助判别谱的周期性,又能精确地测出频率的间隔。
由于超声声表面波检测信号中含有大量噪声,实际检测过程中通常要对信号进行消噪处理。相关函数通过检测回波的最大峰值来确定时差,当最大峰值比较小时,经过滤波(消噪)后实际上不可能加以检测,但是采用倒频谱分析方法往往还能显示出延时峰,这种对整个谱的形状不敏感性使倒频谱分析具有更广泛的应用前景。

图5 实际检测信号时域图Fig.5 Time-domain map of detection signal

图6 信号时延分析结果对比Fig.6 Contrast of signal delay analysis result
采用2.5 GHz采样频率的采集系统对激光熔覆试件的表面波应力进行检测,耦合剂采用机油,实验温度为21℃。试件基体材料为45钢,熔覆层材料为Fe901合金粉末。采用连续波Nd:YAG激光器、同步送粉方法,通过多道搭接多层堆积制备激光熔覆试件。在材料试验机上进行逐级拉伸加载。图5(a)、(b)分别为34 MPa、230 MPa应力作用下超声声表面波信号图。从图5可以看出,采集到的表面波信号含有大量噪声。图6为采用倒频谱分析和相关分析结果图。由于采样点数量比较大,表面波的速度变化很微弱,因此对分析结果进行了局部放大,如图6(b)、(c)所示,可以看出两信号之间的时差为20个采样点(8ns)。相关法分析结果信噪比较低,时延峰与周围的干扰信号很接近,不便于精确定位;倒频谱分析结果信噪比较高,时延峰很尖锐,便于精确定位。
3 结论
在超声声表面波应力检测技术中,由于应力引起的速度变化很微弱,并且检测信号会受到噪声的干扰,因此时间差的精确读取是超声无损检测方法的关键技术。传统的相关法无法精确地辨别表面波超声波的声时差。文中提出基于复数倒频谱的表面超声波声时差估计算法,采用该算法对计算机模拟信号和实际检测信号做了声时差分析,并与相关法的时间分析结果做了对比,计算机模拟和实验结果均表明,倒频谱分析方法是一种精度高,具有一定抗干扰能力的声时差估计算法。最后结合表面超声波检测信号的特点,从理论上分析了复数倒频谱分析方法优于相关法的原因。
[1] Junge M,Jianmin Q,Jacobs L J.Relationship between Rayleigh wave polarization and state ofstress[J].Ultrasonics,2006(44):233-237.
[2]Akhshik S,Moharrami R.Improvement in accuracy of the measurements of residual stresses due to circumferential welds in thin-walled pipe using Rayleigh wave method[J].Nuclear Engineering and Design,2009(239):2201-2208.
[3]Husson D.A perturbation theory for the acoustoelastic effect of surface waves[J].American Institute of Physics,1985,57(5):1562-1568.
[4]Duquennoy M,Ouaftouh M,Qurak M.Ultrasonic evaluation of stress in orthotropic materials using rayleigh waves[J].NDE&E International,1999,32:189-199.
[5]Duquennoy M,Ouaftouh M,Ourak M.Determination of stresses in aluminium alloy using optical detection of rayleigh waves[J].Ultrasonics,1999,37:365-372.
[6] Ditri J J.Determination of nonuniform stresses in an isotropic elastic half space from measurements of the dispersion of surface waves[J].J.Mech.Phys Solids,1997,45:51-66.
[7]华 容,等.信号分析与处理[M].北京:高等教育出版社,2004.
[8]Lester W,Schmerr J,Sung J S.Ultrasonic nondestructive evaluation systems:models and measurements[M].New York:Springer,2007.
[9]Lester W, Schmerr J. Fundamentals of ultrasonic nondestructive evaluation:a modeling approach[M].New York:Plenum Press,1998.
[10]林 莉,李喜孟.超声波频谱分析技术及其应用[M].北京:机械工业出版社,2009.
