结构参数对机翼非线性颤振系统混沌运动特性的影响

张 惠，杨智春，张新平，周 建，谷迎松

(1.西北工业大学 航空学院结构动力学与控制研究所，西安 710072;2.中航陕西飞机工业(集团)公司设计院，陕西 汉中 723213)

机翼的混沌运动是飞机在达到一定飞行速度后，在气流激励下由于结构的弹性力、惯性力和气动力的耦合作用而产生的一种气动弹性失稳现象。带有结构非线性的机翼颤振可能呈现混沌振动的形式［1］，混沌运动在相空间中没有确定的轨道，使得用常规的振动控制技术来抑制非线性颤振难以获得预期的效果。同时，混沌的出现有时伴随有周期窗口［2-3］，周期窗口将会打破混沌颤振区域的连续性而使得系统的混沌颤振控制更加困难，因此选取合适的结构参数来避免在混沌颤振区域内出现周期窗口，对混沌颤振运动的研究和控制具有重要意义。

目前，国内外学者已经在非线性动力学系统的混沌运动及其周期窗口的控制方面开展了一些研究，例如:Hekmatollah Alighanbari指出具有结构非线性的机翼颤振系统的参数对其混沌运动有强烈影响［4］。杨怀江和沈柯明确提出了一种光学混沌控制技术——周期窗口控制技术以及为解决周期窗口找寻困难而开发的周期窗口搜索及定位技术［5］;郑国勇和杨翊仁指出超音速气流中的二元机翼在速度比线性颤振速度高且在初始条件非常小时，会出现混沌运动［6］。以一个具有立方型非线性操纵刚度的带操纵面二元机翼［7］为研究对象，基于能量方法和活塞气动力理论建立起系统的颤振运动方程，采用数值分析方法分析结构参数对非线性颤振系统混沌运动特性以及对混沌颤振区域内周期窗口的影响，提出一种在不降低系统颤振临界速度的前提下有效控制混沌颤振区域内周期窗口的方法。为合理选择设计参数，最终控制系统的混沌颤振运动提供了一条技术途径。

1 系统的运动微分方程

带有操纵面的二元机翼颤振系统如图1所示，该系统具有3个自由度，分别为机翼上下沉浮h，绕弹性轴的扭转角α以及操纵面绕铰链轴的偏转角β。假定操纵面偏转自由度上具有立方型非线性刚度，其刚度特性为Mβ=Kβ(β+eβ3)(e为非线性系数)，由拉格朗日方程可建立带操纵面二元机翼的无量纲化颤振运动方程［8］:

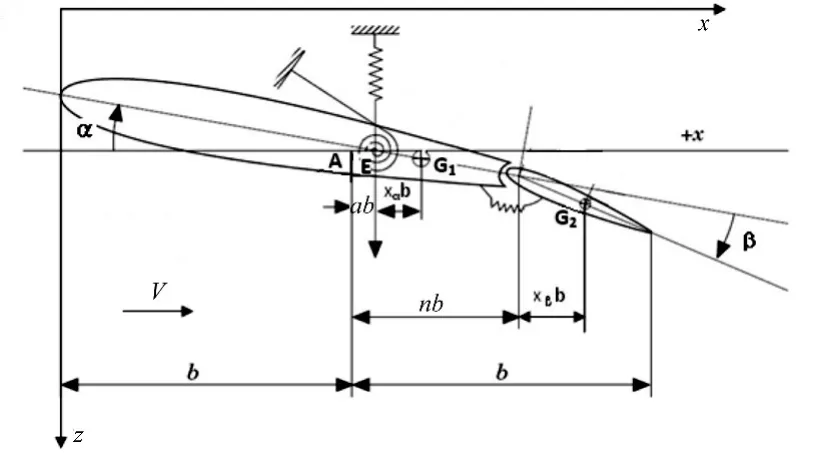
图1 带操纵面的二元机翼示意图Fig.1 The sketch of airfoil with control surface

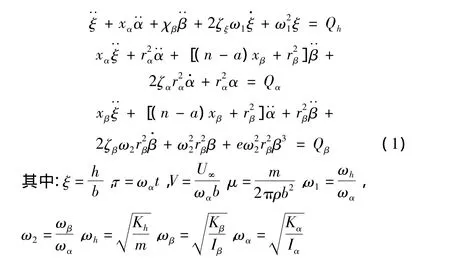
nb为操纵面铰链轴到翼弦中点的距离，xα为机翼重心距刚心的无量纲距离，xβ为操纵面重心到铰链轴的无量纲距离，rα为机翼对刚心的无量纲回转半径，rβ为操纵面对铰链轴的无量纲回转半径。

采用活塞气动力理论计算广义气动力［8］:

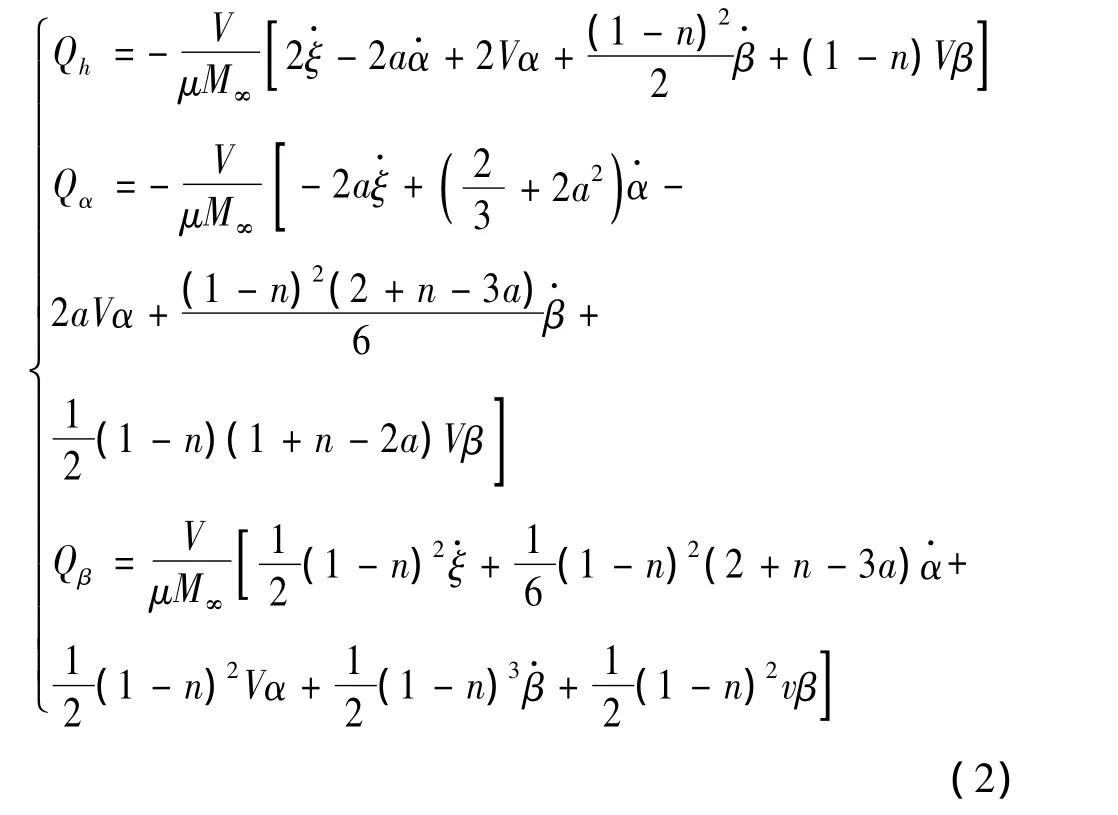
将(2)式代入(1)式，则可写成如下的矩阵形式:

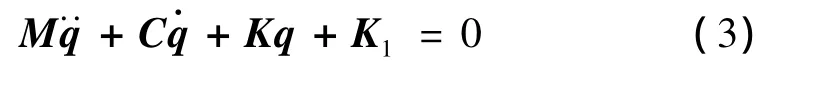
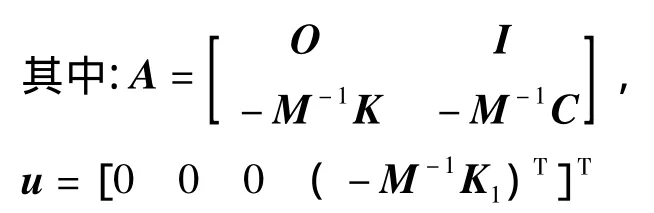
O为3阶零矩阵，I为3阶单位矩阵。

2 混沌运动特性分析

作为非线性动力学系统，当初始条件确定后，其动力学行为将主要取决于系统的结构参数，本文研究的二元机翼非线性颤振系统的结构参数见表1。对于具有非线性操纵刚度的带操纵面二元机翼，以无量纲来流速度V作为控制参数，采用数值积分的方法，对颤振运动方程进行求解，计算得到操纵面偏转自由度位移幅值的分岔特性图。通过分岔特性图来分析非线性操纵刚度、俯仰自由度及操纵面偏转自由度上的阻尼对非线性颤振系统混沌运动特性的影响。

在分岔图中出现混沌的区域中，可以清楚地看到参量取值(横坐标)在某些狭窄的范围内出现周期震荡，这就是混沌区内的周期窗口［10］。对于周期窗口采用了直接观测法，在对应的分岔图中，出现混沌的区域内，幅值分布明显缩小的速度区间，就是出现周期窗口的速度区间。如果画出对应参数状态下的相图，将会观察到明显的极限环。

系统的混沌颤振区域中有一类周期窗口，相对于其它周期窗口，其长度一般都较长，称为主周期窗口。还有一些相对并不十分明显的周期窗口，它们的窗口长度一般都较短，且出现位置没有规律性，称为次周期窗口。我们可以通过研究非线性颤振系统混沌颤振区域内周期窗口的个数以及主周期窗口和次周期窗口出现的区间长度来研究结构参数的变化对非线性颤振系统混沌运动特性的影响。

2.1 操纵面的立方型非线性操纵刚度对混沌运动特性的影响

在本文研究的机翼非线性颤振系统的结构参数中，操纵面的操纵刚度系数(代表非线性的强弱程度)为重要的参数之一。在其它结构参数固定不变的情况下，通过改变操纵面的操纵刚度非线性系数来研究系统在不同强弱程度的非线性操纵刚度下的混沌运动特性。对立方型非线性操纵刚度，其等效刚度系数为Keq=Kβ(1+3/4eβ2)。因此可以通过改变非线性参数e来研究非线性操纵刚度对系统混沌运动特性的影响。取俯仰自由度上的阻尼系数ζα=0.14，操纵面偏转自由度上的阻尼系数ζβ=0.16，经过数值积分分别得出e=5，10，20，40 时系统的分岔图如图 2(a)～ 图 2(d)所示。(图中的速度为无量纲速度)

观察图2(a)～图2(d)可知，当e改变时，系统的分岔特性基本不变，系统操纵面偏转自由度上的颤振幅值随着e的增大而减小。e变化时，系统出现主周期窗口及次周期窗口的无量纲速度区间基本相同。系统出现主周期窗口的无量纲速度区间为［4.15，4.35］，出现两个狭窄的次周期窗口的无量纲速度区间为［4.51，4.54］和［4.74，4.77］。

由此可见，对于本模型而言，系统是否产生混沌运动，混沌颤振区域内是否出现周期窗口以及周期窗口对应的无量纲速度区间几乎不受参数e的影响。因此，通过改变操纵刚度非线性强弱程度来控制系统混沌现象的发生以及控制混沌颤振区域内的周期窗口是不可能实现的。但是，适当提高操纵面的操纵刚度系数，可以使系统发生非线性颤振时的幅值减小，从而降低非线性系统发生颤振时的危害性。

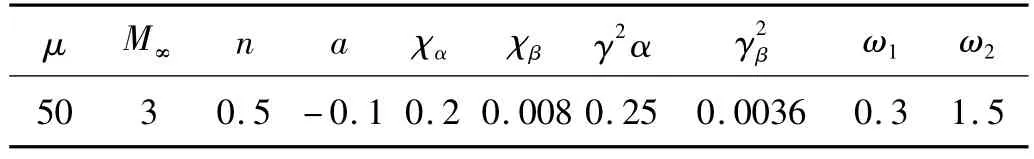
表1 机翼颤振系统的结构参数Tab.1 The structural parameters of the airfoil flutter system

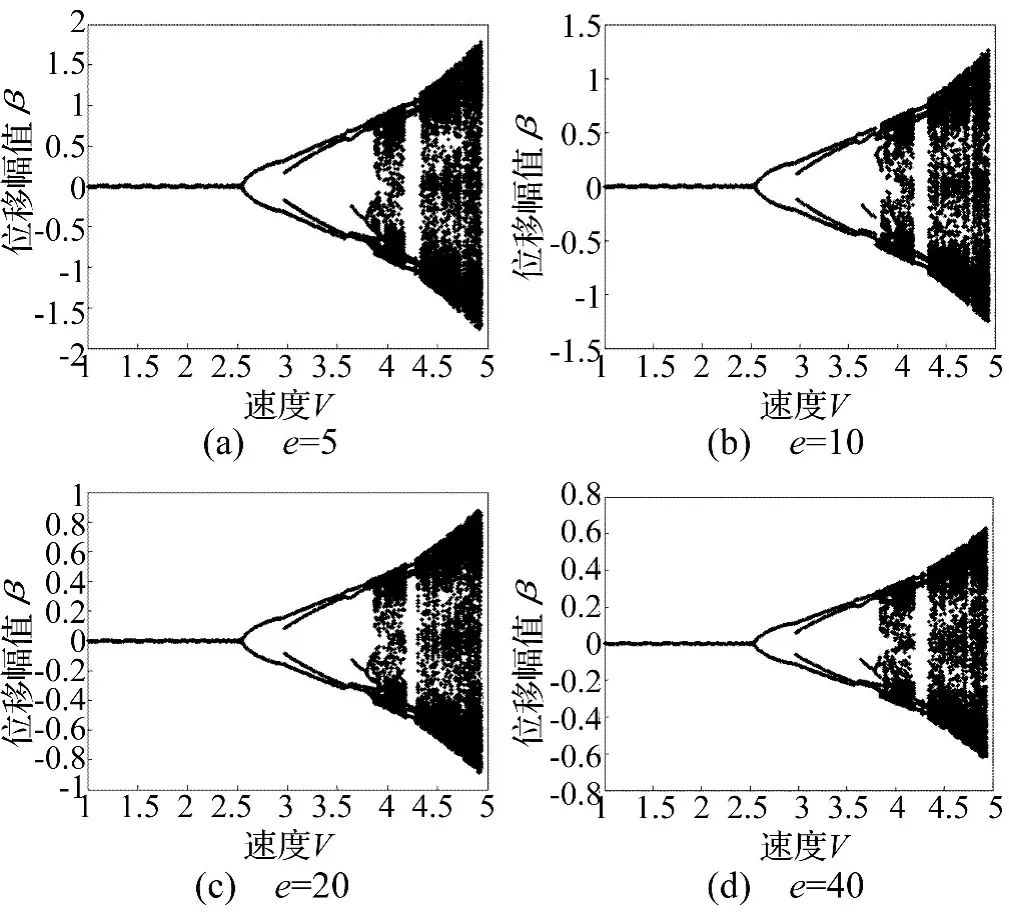
图2 不同非线性操纵刚度参数下的系统分岔特性Fig.2 The characteristic of the system at the different nonlinear stiffness of the control surface

2.2 操纵面偏转自由度的阻尼对系统混沌运动特性的影响

在带操纵面的二元机翼非线性颤振系统中，操纵面偏转自由度上的阻尼也是系统的一个重要参数。研究操纵面偏转自由度的阻尼对系统混沌运动特性的影响时，取操纵刚度非线性系数e=10，俯仰自由度上的阻尼系数ζα=0.14，操纵面偏转自由度上的阻尼系数分别为 ζβ=0.01，0.03，0.05，0.08，0.10，0.20 时，系统的分岔特性图如图3(a)～图3(f)。

当操纵面偏转自由度上的阻尼系数ζβ=0.01时，如图3(a)所示，系统只有衰减与发散两种运动形式，系统的无量纲颤振临界速度为VF=1.15。当 ζβ=0.03和0.05时，如图3(b)和3(c)所示，随着速度的逐渐增大，系统经历衰减运动、极限环运动、混沌运动以及发散运动四种运动形式，但是混沌颤振区域内没有周期窗口的出现，系统的无量纲颤振临界速度分别为VF=2.20 和2.27。当 ζβ=0.08 时，如图3(d)所示，系统在混沌颤振区域内会出现一个小的周期窗口，其无量纲速度区间为［3.86，3.88］，系统的无量纲颤振临界速度为VF=2.38。当 ζβ=0.10 时，如图 3(e)所示，混沌颤振区域内会出现三个小的周期窗口，对应的无量纲速度区间分别为［3.82，3.88］，［4.20，4.23］，［4.23，4.25］，系统的无量纲颤振临界速度为VF=2.45。当阻尼系数ζβ=0.20时，如图3(f)所示，系统的无量纲颤振临界速度为VF=2.64，主周期窗口的速度区间为［4.72，4.86］，次周期窗口的速度区间分别为［5.10，5.15］和［5.31，5.35］。

上述分析表明，随着操纵面偏转自由度上的阻尼的增大，系统的分岔特性会发生改变，当操纵面偏转自由度上的阻尼增大到某个水平时，混沌颤振区域将出现周期窗口，且周期窗口对应的无量纲速度区间长度会随着操纵面阻尼水平的提高而增大，同时系统的无量纲颤振临界速度会随着操纵面偏转自由度上阻尼的增大而提高。因此，对于非线性颤振系统，虽然降低操纵面偏转自由度上的阻尼水平，可以使混沌颤振区域内的周期窗口得以控制甚至使混沌现象消失，如图3(a)所示，但是系统的颤振临界速度也会随之降低。

2.3 俯仰自由度的阻尼对混沌运动特性的影响

对带有操纵面的二元机翼，其俯仰自由度的阻尼也是系统可控的一个重要参数，本节研究俯仰自由度的阻尼对系统混沌运动特性的影响。

取操纵面偏转自由度上的阻尼系数ζβ=0.16，操纵刚度非线性系数e=10，俯仰自由度上的阻尼系数分别取为 ζα=0.01，0.05，1。系统的分岔特性图如 4(a)～图4(c)。

当俯仰自由度上的阻尼系数ζα=0.01时，如图4(a)所示，随速度增加，系统经历衰减运动，极限环颤振以及发散颤振三种运动形式。系统的无量纲颤振临界速度为VF=1.89。当 ζα=0.05 时，如图 4(b)所示，系统在来流速度V=3.08时出现混沌运动，但是在系统的混沌颤振区域内没有周期窗口的出现，其无量纲颤振临界速度为VF=2.38。当 ζα=0.10 时，由图4(c)可以看出，系统的无量纲颤振临界速度为VF=2.48。系统在混沌颤振区域内出现第一个主周期窗口的无量纲速度区间为［3.81，3.87］，系统出现第二个周期窗口的无量纲速度区间为［4.14，4.22］。这两个周期窗口的区间长度比俯仰自由度阻尼系数ζα=0.14时(如图2(b))的周期窗口的区间长度要短。

上述结果表明，当俯仰自由度上的阻尼减小时，系统的混沌运动和周期窗口都可以得到控制，而且其无量纲颤振临界速度的变化没有操纵面偏转自由度上的阻尼系数减小时变化得那么剧烈。

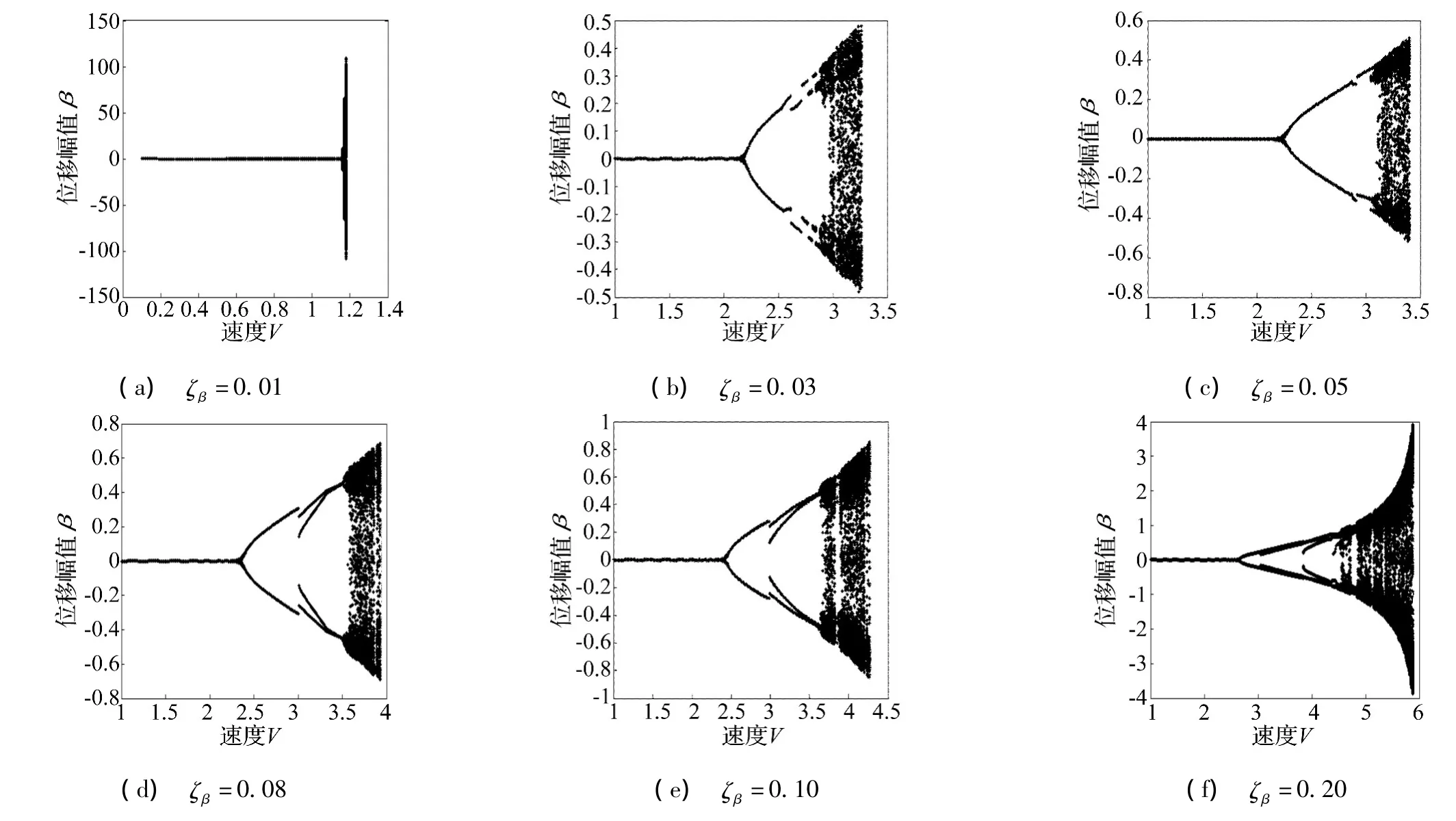
图3 不同操纵面偏转自由度阻尼水平下的系统分岔特性Fig.3 The bifurcation characteristic of the system at the different damping coefficients in the rotating DOF of control Surface

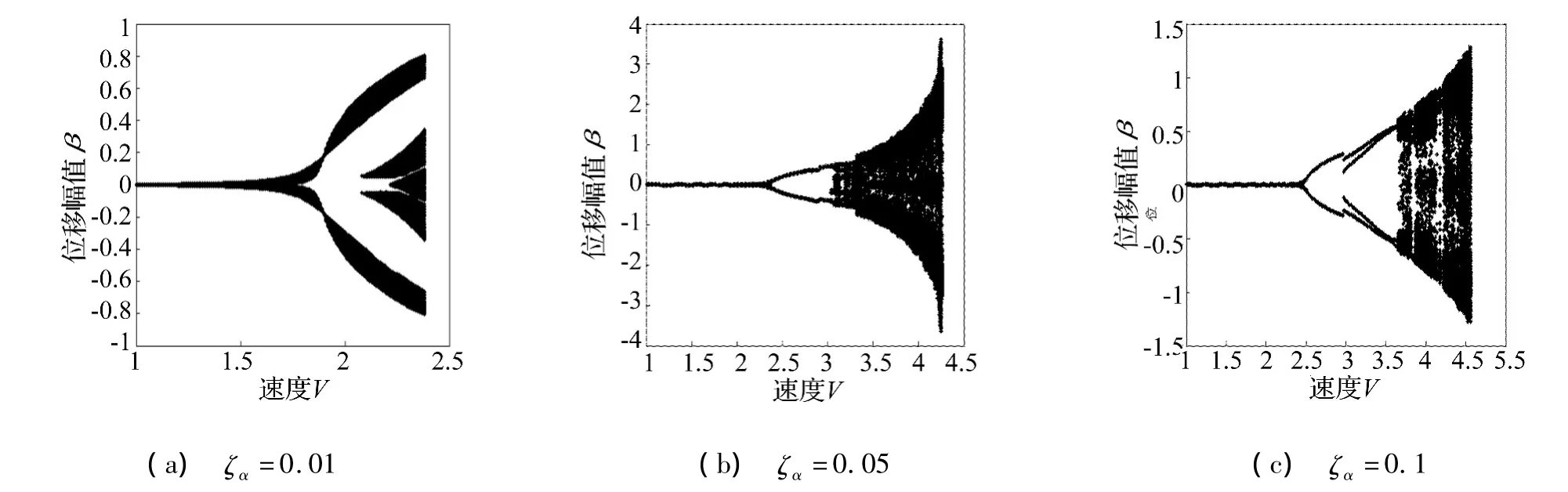
图4 不同俯仰自由度阻尼水平下的系统分岔特性Fig.4 The bifurcation characteristic of the system at the different damping coefficients in the pitching DOF of wing

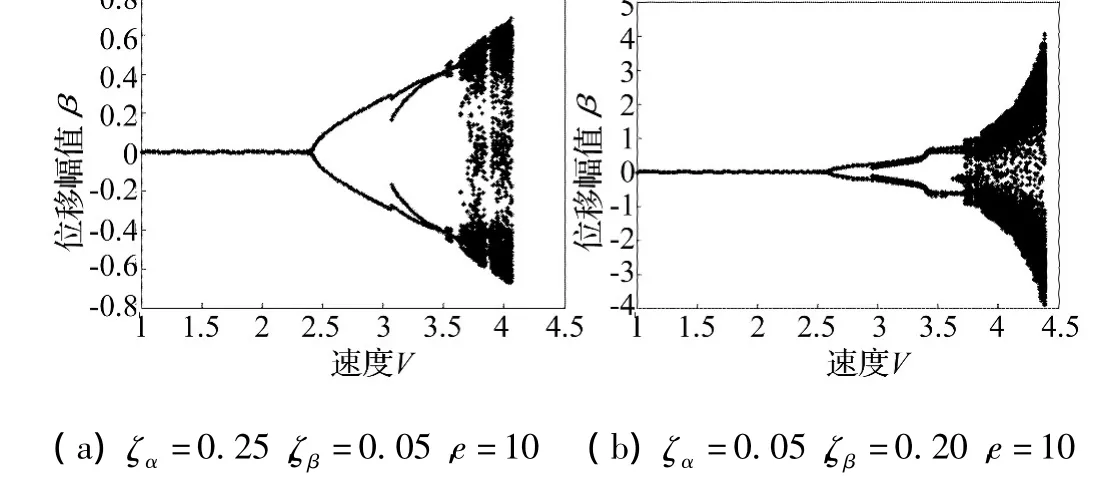
图5 同时改变操纵面自由度和俯仰自由度阻尼水平时系统的分岔特性Fig.5 The bifurcation Characteristic of the system when changing the damping coefficient in the rotating DOF of control surface and the pitching DOF of wing

2.4 同时改变俯仰自由度和操纵面偏转自由度的阻尼对系统混沌运动特性的影响

通过前面的分析知，单一的减小俯仰自由度上的阻尼或者操纵面偏转自由度上的阻尼，虽然可以控制系统的混沌运动以及混沌颤振区域内的周期窗口，但是，系统的无量纲颤振临界速度会随着阻尼系数的减小而降低。这并不是我们所期待的结果。所以，需要寻求一种在颤振临界速度不变或者有所提高的前提下来控制系统周期窗口的方法。

以参数 ζα=0.14，ζβ=0.16，e=10 时系统的混沌运动特性为参考来进行研究。当俯仰自由度上的阻尼系数为ζα=0.25，操纵面偏转自由度上的阻尼系数为ζβ=0.05时，虽然系统的无量纲颤振临界速度不变，但是混沌颤振区域内的周期窗口依然没有消失，如图5(a)所示。但是当俯仰自由度上的阻尼系数减小到ζα=0.05的同时，将操纵面偏转自由度上的阻尼系数增大到ζβ=0.20时，此时系统的无量纲颤振临界速度不仅有所提高，而且混沌颤振区域内的周期窗口消失了，如图5(b)所示。

因此，可以采用减小俯仰自由度上的阻尼水平同时增加操纵面偏转自由度上阻尼水平的方法，在保证颤振临界速度不降低的情况下消除机翼非线性颤振系统混沌颤振区域内的周期窗口，从而能更好控制系统的混沌运动。

3 结论

(1)操纵面刚度的非线性强弱程度对非线性颤振系统出现混沌运动的速度区间影响很小。

(2)改变二元机翼俯仰自由度或操纵面偏转自由度阻尼水平可以改变系统的混沌运动特性，即可以通过改变操纵面偏转自由度或者机翼俯仰自由度上的阻尼水平来控制系统混沌颤振区域内的周期窗口。

(3)单一的改变操纵面偏转自由度或者机翼俯仰自由度上的阻尼水平，系统的无量纲颤振临界速度会随着阻尼水平的降低而减小。

(4)为了保证系统颤振临界速度不会减小，可以采用同时改变俯仰自由度上的阻尼水平与操纵面偏转自由度上阻尼水平的方法来控制系统混沌颤振区域内的周期窗口。

［1］Zhao L C，Yang Z C.Chaotic motions of an airfoil with nonlinear stiffness in incompressible flow［J］.Journal of Sound and Vibration，1990，138(2):245-254.

［2］任爱娣，张良欣，张琪昌.具有不对称间隙的二元机翼自激振动的混沌分析［J］.空气动力学学报，2009，27(3):89-92.REN Ai-di，ZHANG Liang-xin，ZHANG Qi-chang.The chaos study of a two-dimensional airfoil with asymmetry freeplay［J］.Acta Aerodynamica Sinica，2009，27(3)，89-92.

［3］ Zhao D M，Zhang Q C.Bifurcation and chaos analysis for aeroelastic airfoil with freeplay structural nonlinearity in pitch［J］.Chinese Physical Society and IOP，2010，19(3):030518-1-030518-10.

［4］ Hekmatollah A.Flutter analysis and chaotic response of an airfoil accounting for structural nonlinearities［D］.Canada:McGill University，Canada，1995.

［5］杨怀江，沈 柯，翁兆恒，等.光学混沌之周期窗口控制技术［J］.激光技术，1996，20(5):282-284.

YANG Huai-jiang，SHEN Ke，WENG Zhao-heng，et al.Control technique of optical chaos for period windows［J］.Laser Technology，1996，20(5):282-284.

［6］Zheng G Y，Yang Y R.Chaotic motions and limit cycle flutter of two-dimensional wing in supersonic flow［J］.Acta Mechanica Solida Sinica，2008，21(5):442-448.

［7］Irani S，Sarrafzadeh H，Amoozgar M R.Bifurcation in a 3-DOF Airfoil with Cubic Structural Nonlinearity［J］.Chinese Journal of Aeronautics，2011，24(3):265-278.

［8］郑国勇，杨翊仁.具有操纵面立方非线性机翼的混沌响应［J］.工程力学，2010，27(2):209-221.

ZHENG Guo-yong，YANG Yi-ren.Chaotic motion of a two dimensional wing with control surface cubic nonlinearity［J］.Engineering Mechanics，2010，27(2):209-221.

［9］张琪昌.分岔与混沌理论及应用［M］.天津:天津大学出版社，2005.

［10］刘秉正，彭建华.非线性动力学［M］.北京:高等教育出版社，2004.